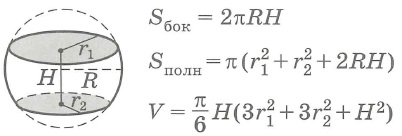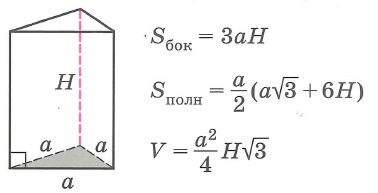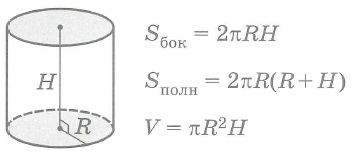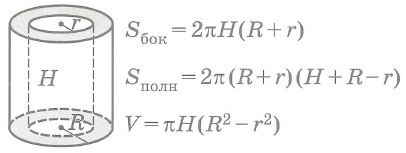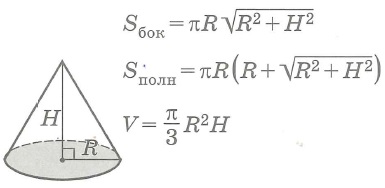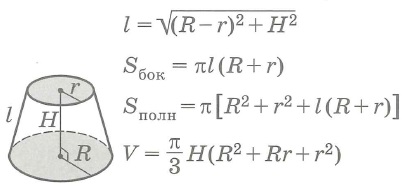|
|
индивидуальное проектирование по математике 1 курс. Индивидуальное Проэктирование-Математика АК7-19 Мерешко. Презентация по индивидуальному проэктированию На тему Площадь и объем геометрических тел. Выполнил студент Группы ак719
Министерсво образования
Республики Башкортостан
ГБПОУ Уфимский
автотранспортный колледж.
Презентация по - . индивидуальному проэктированию
На тему:
Площадь и объем геометрических тел.
Выполнил студент
Группы АК7-19
Мерешко С.
Проверил
Преподаватель
Габрафикова Г.Ф.
Уфа 2020
Цель:научится использовать формулы и решать задачи при помощи заданных формул.
1.Обоснование темы:
Пло́щадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры, неформально говоря, показывающая размер этой фигуры. Исторически вычисление площади называлось квадратурой.
Объём — количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами.
Те́ло геометри́ческое — «то, что имеет длину, ширину и глубину» в «Началах» Евклида, в учебниках элементарной геометрии ко всему «часть пространства, ограниченная своей образуемой формой».
Глава 1-ая:теоретическая часть иследования
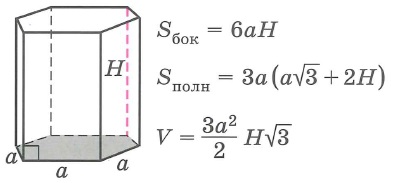
Прямые призмы (Sполн=2Sосн+Sбок; V=Sосн•H)
|
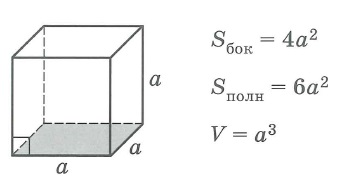
Куб
|
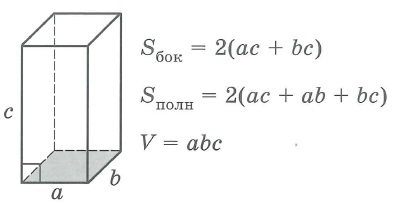
Прямоугольный параллелепипед
|
Правильная треугольная призма
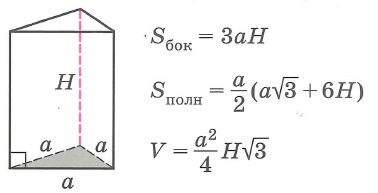
|
Правильная шестиугольная призма
|
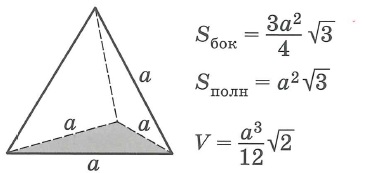
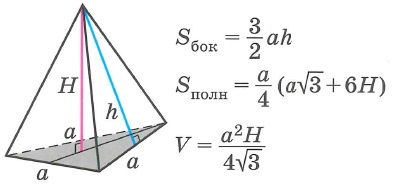
Правильные пирамиды (Sполн=Sосн+Sбок; V=1/3•Sосн•H)
|
Тертраэдр
|
Правильная треугольная пирамида
|
Правильная четырехугольная пирамида
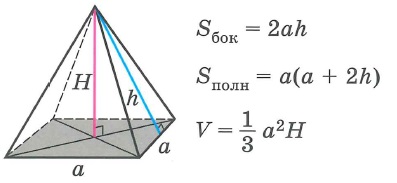
|
Правильная шестиугольная пирамида
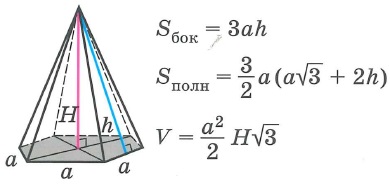
|
Sбок- площадь боковой поверхности многогранника, Sполн - площадь полной поверхности многогранника, Sосн - площадь основания многогранника, V - объем многогранника.
|
Круговые цилиндры (Sполн=2Sосн+Sбок; V=Sосн•H)
|
Прямой цилиндр
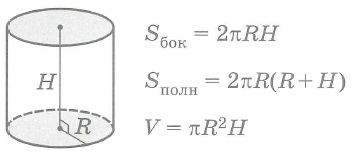
|
Прямой полый цилиндр
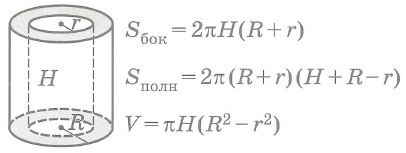
|
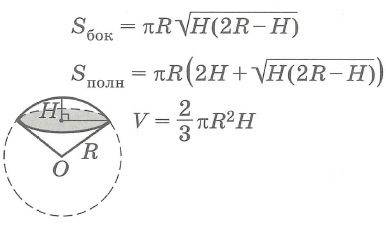
Круговые конусы
|
Прямой конус
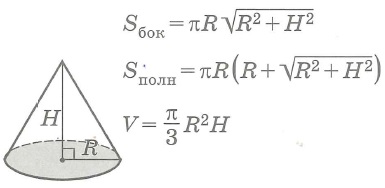
|
Прямой усеченный конус
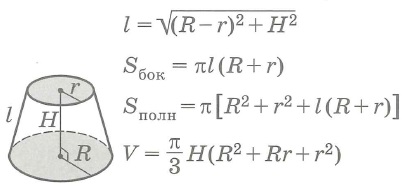
|
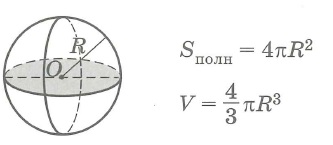
Шар и его части
|
Шар
Шаровой слой
|
|
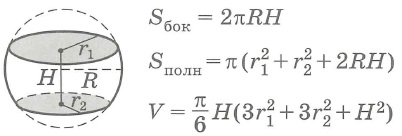
Шаровой сектор 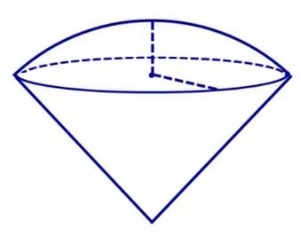 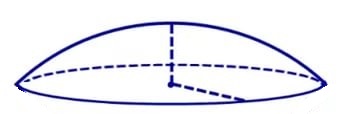
Шаровой сегмент
|
Шаровой сегмент
|
Sбок- площадь боковой поверхности круглого тела,
Sполн - площадь полной поверхности круглого тела,
Sосн - площадь основания круглого тела, V - объем круглого тела.
Глава 2-ая:практическая часть иследования
2.1-куб
Дан куб ABCDA1B1C1D1. Точка B2 лежит на продолжении ребра BB1 за точку B1, BB2=2⋅BB1.
Во сколько раз объем куба отличается от объема пирамиды B2ABCD?
Решение: Отрезок BB2 является высотой пирамиды. Если сторону куба обозначить за x, то BB2=2x ⇒ п и р к у б Vпир.=13⋅BB2⋅SABCD=13⋅2x⋅x2=23⋅x3,Vкуб=x3.
Теперь найдем искомую величину: к у б п и р VкубVпир.=x323⋅x3=1,5. Ответ: 1,5
2.2-шар
Задача: Объем шара равен 36π. Чему будет равна площадь поверхности шара, если его радиус увеличить на 6π?
Решение ш а р а Vшара=43πR3=36π ⇒ R=3π. Радиус нового шара равен: н о в Rнов.=R+6π=9π.
Тогда найдем площадь поверхности: п о в н о в Sпов.=4πRнов.2=4π(9π)2=4π81π=324. Ответ: 324
2.3-перамида
Задача: В пирамиде SABC высота SO падает в точку пересечения медиан основания.
Треугольник ABC равнобедренный, боковые стороны равны 10, а основание AC=18.
Найдите объем пирамиды, если известно, что угол между боковым ребром SB и плоскостью основания равен 45∘.
Решение: Пусть BK – высота в △ABC, а значит и медиана.
Тогда из прямоугольного △BKC: BK=BC2−KC2=102−92=19.
Тогда площадь основания равна SABC=12⋅AC⋅BK=919.
Так как O – точка пересечения медиан, то O лежит на BK.
Так как медианы точкой пересечения делятся в отношении 2:1, считая от вершины, то BO=23BK=2319.
Заметим, что угол между прямой и плоскостью – это угол между прямой и ее проекцией на плоскость, следовательно, ∠SBO=45∘ и есть угол между SB и основанием (так как BO – проекция SB на плоскость ABC).
Так как к тому же △SBO прямоугольный, то он равнобедренный, следовательно, SO=BO=2319.
Тогда объем пирамиды равен V=13⋅SO⋅SABC=38. Ответ: 38
Закключение:
1.При помоши этих формул можно найти площадь и объем
Геометрических фигур:Первым делом находим площадь фигур,а уже
Потом при помощи площади найдем объем.
2. Используя эти формулы я научился находить объем и площадь фигур
используя более легкий и простой способ,тем самым ускорив процесс решения задач связанных с геометрическими фигурамиэ.
3.Данная информация может пригодится при чертежах,ремонте
автомобилей(их состовляющих),для учеников 7-11 класса,а также для обучения учеников опираясь на эти формулы.
Литература:
Учебник по математике за 7-11 класс,
Сайт с формулами(https://dpva.ru)
Методическая рекомендация(https://nsportal.ru/npo-spo/estestvennye-nauki/library/2017/02/08/metodicheskie-rekomendatsii-po-ip)
Сайты по типу : https://otvet.mail.ru , https://znanija.com .
| |
|
|
 Скачать 340.9 Kb.
Скачать 340.9 Kb.