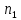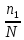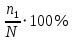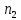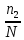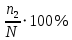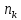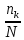Вкр. При Президенте Российской Федерации
 Скачать 1.12 Mb. Скачать 1.12 Mb.
|
|
Глава 2. Исследование алгоритмов анализа данных рынка арендного жилья 2.1. Подготовка данных для анализа Первый этап построения математической модели заключается в формировании статистической выборки, на базе которой будет строиться аналитическая работа. Статистическая выборка – это набор информации, который представляет собой определенную часть из общего объема данных по исследуемому объекту, отобранный для проведения аналитических работ. Статистическая выборка отбирается из генеральной выборки (из совокупности всех элементов данных по исследуемому объекту). От статистической выборки требуется соответствие следующим критериям: Репрезентативность (представительность): Выборке необходимо максимально отражать свойства всего объема статистических данных по исследованному объекту; Соответствие структуре генеральной выборке; Иметь не менее 150 элементов. Основной целью формирования статистической выборки является эффективное использование ее составных элементов в качестве исходной информации для получения достоверных результатов по общему объему объектов генеральной совокупности; Первичный анализ. Данный этап состоит из сегментирования и составления описательной статистики. Сегментирование заключается в группировке данных или в разбиении на диапазоны всех значений конкретно рассматриваемого величины на интервалы с дальнейшем подсчетом числа наблюдений, попавших в ту или иную группу (карман). Этот способ позволяет оценить процентное соотношение разных значений величины и в каких интервалах значений исследуемая величина встречается. Подобный подход позволяет преобразовать неупорядоченный набор выборочных данных так, что становится ясным и наглядным, насколько часто значения исследуемой величины появляются в том или ином диапазоне ее значений. Формальный алгоритм группировки данных заключается в нахождение минимального и максимального значения по выборочным данным и распределением диапазона между ними на карманы (интервалы) одинаковой длины (для сохранения информативности до 15 интервалов). Далее ведется подсчет наблюдений в каждом интервале и рассчитывается относительная частота значений рассматриваемой величины. Математическое описание формального алгоритма группировки данных1: Таблица 2.2 Математическая характеристика группировки данных
Описание величин, представленных в таблице 2.2: Ymin – минимальное значение; Ymax – максимальное значение; ni — число наблюдений, попавших в i-й интервал [Yi−1, Yi]; N — объем выборки. Составление описательной статистики заключается в следующих числовых характеристиках, которые вычисляются с использованием инструмента «описательная статистика»: Среднее арифметическое – простое средние значение по выборке исследуемой величины; Медиана – значение исследуемой величины, по обоим сторонам координат которого одинаковое количество упорядоченных по возрастанию данных выборки; Мода – значение исследуемой величины, которое наиболее часто встречается среди данных выборки; Стандартное отклонение – значение степени разброса значений исследуемой величины относительно среднего значения. Анализ алгоритмов обработки данных об арендных помещениях Факторный анализ. Данный этап комплексного анализа состоит из построения однофакторных регрессионных моделей и вычислением коэффициентов корреляции. Построение однофакторной регрессионной модели заключается в формировании точечного графика с выявлением тренда изменения арендной ставки торговых помещений в зависимости от рассматриваемого фактора. Точечный график позволяет проанализировать влияние рассматриваемой переменной x (выбранного фактора) на величину y (ставки аренды торгового помещения) и дает наглядное представление об особенностях исследуемой величины. Рассматриваемые зависимости могут иметь высокий разброс значений и при большем количестве данных, с помощью графика трудно сделать вывод о зависимости рассматриваемой величины. Для улучшения качества анализа определяется тренд зависимости на точечном графике. Для формирования тренда проводится процедура аппроксимации – замена точек, лежащих на графике на такую кривую y = f(x), которая наилучшим образом отражает зависимость величины y от переменной x. Далее представлены основные способы аппроксимации: Линейный. Используется для линейной аппроксимации данных по методу наименьших квадратов в соответствии с уравнением: 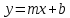 Где m – коэффициент наклона кривой, b - координата пересечения оси абсцисс. Степенная. Используется для степенной аппроксимации данных по методу наименьших квадратов в соответствии с уравнением: 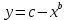 Где c и b - константы. Логарифмический. Используется для логарифмической аппроксимации данных по методу наименьших квадратов в соответствии с уравнением: 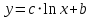 Где c и b - константы, ln - функция натурального логарифма. Экспоненциальная. Используется для экспоненциальной аппроксимации данных по методу наименьших квадратов в соответствии с уравнением: 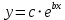 Где c и b - константы, e - основание натурального логарифма. Полиномиальный. Используется для построения криволинейной аппроксимации данных по методу наименьших квадратов в соответствии с уравнением: 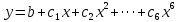 Где b, c1, c2, … c6 - константы. Выбор способа аппроксимации зависит от решения аналитика, исходя из его оценки точечного графика. Для объективного выбора способа и оценки качества, получившиеся аппроксимирующей кривой, используется расчет коэффициента детерминации – R2. Данный коэффициент рассчитывается по следующей формуле: 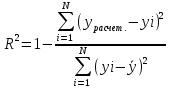 Где 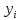 – исследуемая величина; – исследуемая величина;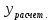 – значения исследуемой величины, вычисленные на основе полученного уравнения кривой тренда; – значения исследуемой величины, вычисленные на основе полученного уравнения кривой тренда;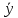 – средние значение исследуемой величины. – средние значение исследуемой величины.Коэффициент детерминации принимает значение от 0 до 1. Чем его значение ближе к 1, тем качественней (точнее) построен тренд на точечном графике. Вычисление корреляционных коэффициентов проводится методом парной корреляции, который определяет степень линейности связи между исследуемой величиной и выбранным переменной (фактором). Формула вычисления парной корреляции: 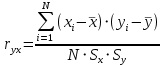 Где 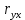 – коэффициент парной корреляции; – коэффициент парной корреляции;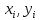 – фактор и исследуемая величина; – фактор и исследуемая величина;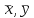 – их средние значения; – их средние значения;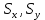 – оценки стандартных отклонений, – оценки стандартных отклонений, N – объем выборки. Коэффициент корреляции принимает значение в диапазоне от -1 до +1. Чем ближе значение коэффициента парной корреляции по абсолютной величине к единице, тем теснее линейная связь. При положительных значениях коэффициента парной корреляции связь между y и x прямо-пропорциональна – увеличение x приводит к увеличению y. Отрицательное значение коэффициента корреляции означает обратно-пропорциональную связь – увеличение x приводит к уменьшению y. Оптимизация выбора арендного предложения. Данный этап состоит из построения многофакторной регрессионной модели и применением кластерного анализа. Построение многофакторной регрессионной модели заключается в вычислении функции, наиболее точно отражающей зависимость исследуемой величины от множества переменных (факторов). Что позволяет разработать инструмент объективной оценки и прогнозирования значений исследуемой величины. Многофакторная регрессионная модель имеет следующую формулу: 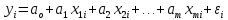 Где: εi — ненаблюдаемая случайная ошибка; x1, x2, xm — влияющие факторы. a0, a1, a2, am — коэффициенты уравнения регрессии, которые необходимо найти. Для нахождения коэффициентов регрессионной модели на основе выборочных данных используется следующая формула: 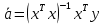 Где: 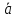 — матрица-столбец коэффициентов множественной линейной регрессии; — матрица-столбец коэффициентов множественной линейной регрессии;y — матрица-столбец выборочных значений исследуемой переменной. x — расширенная матрица факторов. Для оценки качества (точности) многофакторной регрессионной модели вычисляется остаточное стандартное отклонение, которое характеризует разброс выборочных данных относительно расчетных значений регрессионной модели. Вычисление проводятся по следующей формуле: 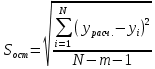 Где: N — объем выборки; m — число факторов в модели; yрасч. — значения исследуемой величины, вычисленные на основе формулы регрессионной модели; yi — выборочные данные. Кластерный анализ заключается в упорядочивании рассматриваемых объектов на сравнительно однородные множества. Данный анализ проводится методом нелинейного программирования с помощью нахождения Евклидова расстояния: минимальной суммы расстояний, которые проходя все жильцы рассматриваемого района от своего дома до рассчитываемой торговой точки. Нахождение Евклидова расстояние имеет следующую формулу: 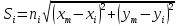 Где: 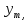 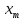 – координаты оптимальной точки; – координаты оптимальной точки;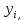 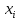 – координаты объектов (жилых зданий); – координаты объектов (жилых зданий);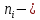 количество жильцов. количество жильцов.Нахождение минимальной суммы Евклидовых расстояний: 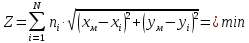 Где: Z – целевая функция. Где: Z – целевая функция.Еще какие-нибудь алгоритмы проанализируйте ( парочку) Выводы по второй главе Исследованы математические алгоритмы, которые чаще всего (вы это узнали из лит источников) применяются для анализа данных, похожих на данные, характеризующие рынок арендных помещений. Перечислите алгоритмы Глава 3. Построение математической модели анализа данных для ….. 3.1 Формирование выборки данных по рынку торговых помещений В рамках данной исследовательской работы генеральной выборкой являются данные об арендном рынке торговых помещений в городе Москве, а статистической выборкой данные объявлений в области, выделенной на ниже представленной карте с предложениями аренды торговых помещений – рис. 1.3 нумерация рисунков разная 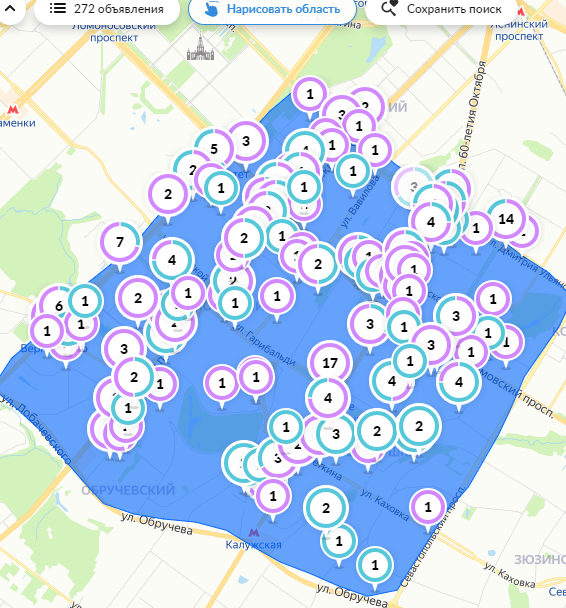 Рис. 2.1 Область, выбранная для формирования статистической выборке по рынку аренды торговых помещений в городе Москве Данная область расположена в Юго-западной округе на стыке трех районов: Ломоносовского, Гагаринского и района Черёмушки. Представленная область выбрана, исходя из следующих положений: Данная область имеет типовые транспортные узлы и одинаковый доступ к станциям метрополитена по всему периметру; На данной области относительно однородная инфраструктура; В рамках одного административного района недостаточное количество заявок для формирования статистической выборки (после форматирования менее 150 наблюдений). Из факторов, влияющих на ставку аренды торговых помещений, было решено исключить факторы, которые описаны в критически малом количестве наблюдений в массиве данных выборки (абсолютное большинство арендных предложений без указания данного параметра): «Класс». Это вызвано тем, что на практике такой способ ранжирования торговых помещений не популярен и нецелесообразен из-за отсутствия общей модели классификации и четких критериев для российского рынка. «Планировка». Так как большинство выставленных в аренду торговых помещений имеет типовую планировку. Так же решено добавить дополнительный фактор «ТЦ/ТРЦ», который означает нахождение торгового помещения в торговом или торгового-развлекательном комплексе. Преобразование качественных данных в количественные (перевод нечисловых значений факторов в числовые): Фактор «ТЦ/ТРЦ»: При значении 1 – торговое помещение находится в ТЦ или ТРЦ; При значении 0 – в ином типе здания. Фактор «Вход»: При значении 1 – торговое помещение имеет собственный отдельный вход; При значении 0 – торговое помещение не имеет отдельного входа. Фактор «Здание»: При значении 1 – торговое помещение находится в жилом здании; При значении 0 – торговое помещение находится в другом типе зданий. На таблице 1.2 представлены все отобранные факторы: Таблица 2.1 Отобранные факторы, влияющие на ставку аренды торгового помещения
После того, как был отредактирован массив данных, была сформирована выборка по арендному рынку торговых помещений в городе Москве объемом 221 (количество наблюдений). |