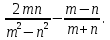МАТЕМАТИКА
Билет № 1
Сложение и вычитание обыкновенных дробей с разными знаменателями. Умножение и деление обыкновенных дробей. Основное свойство дроби. Сокращение обыкновенных дробей.
Определение параллельных прямых. Признаки параллельности прямых. Аксиома параллельных прямых. Теоремы об углах, образованных двумя параллельными прямыми и секущей.
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, а высота фонаря 4 м?
Найдите значение выражения: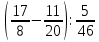 . .
|
Билет № 2
Уравнение и его корни. Линейное уравнение с одной переменной. Алгоритм решения задач с помощью уравнений.
Понятие вектора. Коллинеарные векторы. Равенство векторов. Сложение и вычитание векторов. Умножение вектора на число.
Р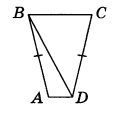 ешите уравнение: ешите уравнение: 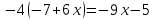 . .
В трапеции ABCD известно, что AB = CD, BDA = 62 и BDC = 42. Найдите ABD.
|
Билет № 3
Степень с натуральным и с целым показателем. Свойства степеней.
Синус, косинус и тангенс острого угла прямоугольного треугольника. Теоремы синусов и косинусов. Решение треугольников.
Решите систему уравнений: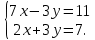
В треугольнике ABC угол С равен 90, AB = 5, 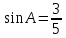 . Найдите AC. . Найдите AC.
|
Билет № 4
Одночлен. Многочлен. Стандартный вид одночлена и многочлена. Сложение и вычитание многочленов. Умножение одночлена на многочлен. Умножение многочлена на многочлен. Привести примеры.
Правильные многоугольники. Окружность, описанная около правильного многоугольника и окружность, вписанная в него. Построение правильных многоугольников.
Решите уравнение: (x + 2)2 = (x − 4)2.
Найдите вписанный угол, опирающийся на дугу, которая составляет 20% окружности. Ответ дайте в градусах.
|
Билет № 5
Способы разложения многочлена на множители. Формулы сокращённого умножения.
Угол между векторами. Скалярное произведение векторов. Перпендикулярные векторы. Условие перпендикулярности двух векторов. Косинус угла между векторами.
Найдите периметр прямоугольника, если одна из его сторон равна 15, а диагональ равна 17.
Упростите выражение: а) 20 · 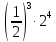 ; б) 7 + 2√5 - √20. ; б) 7 + 2√5 - √20.
|
Билет № 6
Рациональная дробь. Сокращение дробей. Сложение, вычитание, умножение и деление рациональных дробей.
Центральные и вписанные углы. Свойства вписанных углов. Теорема о произведении отрезков пересекающихся хорд.
Упростите выражение: а) 35 · 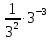 ; б) 5 - 3√7 + √63. ; б) 5 - 3√7 + √63.
Диагонали ромба ABCD пересекаются в точке O и равны 9 и 40. Найдите длину вектора 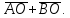
|
Билет № 7
Прямоугольная система координат на плоскости. Понятие функции. Способы задания функции. График функции. Функция у=кх и ее график. Линейная функция и её график. Привести примеры.
Окружность, круг. Длина окружности. Площадь круга.
Дан прямоугольный треугольник АВС, С = 90°, АВ = 13, АС = 5. Найдите косинусугла В.
Найдите значение выражения: 0,8 (-10)4 + 3 (-10)3 + 78.
|
Билет № 8
Система уравнений с двумя неизвестными. Способы решения систем уравнений.Примеры.Алгоритм решения задач с помощью системы уравнений.
Треугольник. Признаки равенства треугольников. Медианы, биссектрисы и высоты треугольника.
Р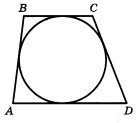 ешитеуравнение: 3х2 + 5х - 2 = 0. ешитеуравнение: 3х2 + 5х - 2 = 0.
Трапеция ABCD с основаниями AD и BC описана около окружности, AB = 9, BC = 7, CD = 11. Найдите AB.
|
Билет № 9
Линейные неравенства с одним неизвестным. Система неравенств с одним неизвестным. Числовые промежутки. Примеры.
Теорема Пифагора. Теорема, обратная теореме Пифагора. Пропорциональные отрезки в прямоугольном треугольнике.
В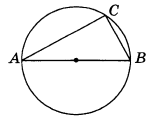 ыполните действия: ыполните действия: 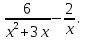
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 33.
|
Билет № 10
Понятие арифметического квадратного корня и его свойства.
Простейшие задачи в координатах: координаты середины отрезка, вычисление длины вектора по его координатам, расстояние между двумя точками.
Р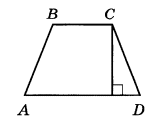 ешите систему уравнений: ешите систему уравнений: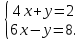
Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 14 и 19. Найдите длину основания BC.
|
Билет № 11
Квадратное уравнения и его корни. Неполные квадратные уравнения.Решение квадратных уравнений. Разложение квадратного трехчлена на множители.
Подобные треугольники. Признаки подобия треугольников. Отношение площадей подобных треугольников.
Упростите выражение: 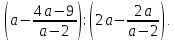
Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 132.
|
Билет № 12
Приведённое квадратное уравнение. Теорема Виета.Алгоритм решения систем, содержащих уравнение второй степени.
Равнобедренный треугольник, его свойства и признаки.
Сократите дробь: 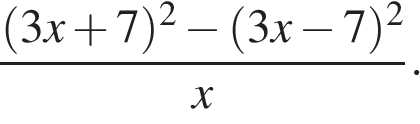
Найдите сторону квадрата, вписанного в окружность радиуса 182.
|
Билет № 13
Определение квадратичной функции. Функции у=х2, у=ах2, у=ax2+bx+c. Построение графика, свойства.
Понятие площади многоугольника.Основные свойства площадей. Площади прямоугольника, параллелограмма, треугольника, трапеции.
На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с яблоками.
В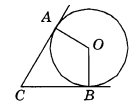 угол С величиной 79 вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. угол С величиной 79 вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB.
|
Билет № 14
Квадратное неравенство и его решение. Решение квадратного неравенства с помощью графика квадратичной функции. Метод интервалов. Примеры.
Вписанная и описанная окружности. При каком условии в окружность можно вписать четырёхугольник. В какой четырёхугольник можно вписать окружность?
Гипотенуза прямоугольного треугольника равна 29. Один из катетов равен 20. Найдите площадь треугольника.
Решите неравенство: x2 + 9x + 20< 0
|
Билет № 15
Целые и дробно-рациональные уравнения. Способы их решения. Примеры.
Прямоугольный треугольник. Свойства прямоугольных треугольников. Признаки равенства прямоугольных треугольников.
Решите неравенство: 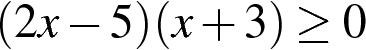
Найдите площадь ромба, если его стороны равны 6, а один из углов равен 150.
|
Билет № 16
Функция y=k/x, ее график и свойства. Привести пример.
Трапеция. Средняя линия трапеции. Виды трапеций. Свойства и признаки равнобедренной трапеции.
Выполните действия: 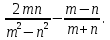
Найдите площадь прямоугольника, если его периметр равен 52, а отношение соседних сторон равно 4 : 9.
|
Билет № 17
Арифметическая прогрессия. Формула n-го члена арифметической прогрессии. Формула суммы n первых членов арифметической прогрессии.
Параллелограмм, его свойства и признаки. Прямоугольник, ромб, квадрат, их свойства.
Расположите в порядке возрастания: √6; 2√3; 3√2; √5.
Найдите углы равнобедренной трапеции, если сумма двух углов этой трапеции равна 220.
|
Билет № 18
Геометрическая прогрессия. Формула n-го члена геометрическойпрогрессии. Формула суммы n первых членов геометрической прогрессии.
Взаимное расположение прямой и окружности. Касательная к окружности, ее свойство и признак. Уравнение окружности.
Решитеуравнение: 5х2 – 16х + 3 = 0.
Угол A четырёхугольника ABCD, вписанного в окружность, равна 46. Найдите угол С этого четырёхугольника.
|
ХИМИЯ
Собеседование по химии представляет собой ответы на вопросы билетов, каждый из которых содержит 2 вопроса и включает в себя следующие задания:
БИЛЕТ 1
1.Окислительно-восстановительные реакции. Окисление и восстановление. Окислитель и восстановитель.
Используя метод электронного баланса, расставьте коэффициенты в уравнении реакции, схема которого
KMnO4 + H2S + H2SO4 → MnSO4 + S + K2SO4 + H2O
Определите окислитель и восстановитель.
2. После пропускания через раствор гидроксида калия 448 мл сернистого газа (н.у.) получили 79 г сульфита калия. Вычислите массовую долю соли в полученном растворе.
|
БИЛЕТ 2
1.Сущность процесса электролитической диссоциации. Диссоциация кислот, оснований и солей.
Напишите уравнения электролитической диссоциации следующих соединений: сульфата калия, ортофосфорной кислоты, гидроксида бария.
2.Сколько граммов 25%-ного раствора азотной кислоты требуется для нейтрализации 250 граммов раствора гидроксда натрия с массовой долей растворенного вещества 0,04.
|
БИЛЕТ 3.
Типы химических реакций. Напишите уравнения реакций между: железом и хлором, сульфидом калия и соляной кислотой.
При взаимодействии аммиака с раствором азотной кислоты получен нитрат аммония массой 240г, выход продукта реакции составил 75%. Какой объем аммиака (н.у.) был использован?
|
БИЛЕТ 4.
1.Строение атома. Электронные оболочки атома.
Определите состав атома углерода. Составьте схему строения атома, электронную формулу атома углерода.
2.При пропускании 5,6 л углекислого газа через 400г раствора гидроксида натрия получили раствор средней соли. Вычислите массовую долю гидроксида натрия в исходном растворе.
|
БИЛЕТ 5.
1.Виды химической связи. Ионная химическая связь. Определите тип химической связи в молекуле хлорида кальция, азота, сероводорода, кальция.
2.Вычислите объем углекислого газа (н.у.), который может выделиться при взаимодействии карбоната калия с 150г раствора азотной кислоты с массовой долей кислоты 6,3%.
|
БИЛЕТ 6.
1.Характеристика элемента по его положению в ПСХЭ Д.И.Менделеева.
Охарактеризуйте магний на основании его положения в ПСХЭ Д.И.Менделеева.
2.К 150 г раствора карбоната натрия добавляли раствор хлорида кальция до прекращения выделения осадка. Масса осадка составила 12г. Вычислите массовую долю карбоната натрия в исходном растворе.
|
БИЛЕТ 7.
1.Виды химической связи. Ковалентная полярная химическая связь. Составьте схему образования химической связи в молекуле сероводорода.
2.Какую массу оксида кальция можно получить при прокаливании 75 г мела, массовая доля примесей в котором 0,05.
|
БИЛЕТ 8.
1.Виды кристаллических решеток. Сравните свойства веществ с ионной и атомной кристаллической решеткой.
2.Какая масса 10%-ного гидроксида калия потребуется для нейтрализации 200г раствора серной кислоты с массовой долей кислоты 7,35%?
|
БИЛЕТ 9.
1.Виды химической связи. Ковалентная неполярная химическая связь. Составьте схему образования химической связи в молекуле азота.
2.Для полного удаления бария из раствора нитрата бария в него добавили 196,8 г раствора фосфата натрия с массовой долей 8%. Определите массу выпавшего осадка.
|
БИЛЕТ 10.
1.Валентность элементов. Правила определения валентности. Составьте формулы соединений, которые состоят из марганца (IV) и кислорода, хлора (VII) и кислорода. Напишите графические формулы этих веществ.
2.При электролизе 585г расплава хлорида натрия было получено 100л (н.у.) хлора. Вычислите выход хлора в процентах от теоретически возможного количества.
|
Литература для подготовки:
Химия. Подготовка к ОГЭ – 2020. 9 класс. 30 тренировочных вариантов по демоверсии 2020 года: учебно-методическое пособие/ под ред. В.Н. Доронькина. – Ростов н/Д: Легион, 2019. – 368с.
Микитюк А.Д. Справочник по химии: 8-9 классы. ФГОС/А.Д. Микитюк. – М.: Издательство «Экзамен», 2019. – 206с.
|
 Скачать 203.02 Kb.
Скачать 203.02 Kb.
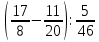 .
. ешите уравнение:
ешите уравнение: 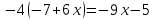 .
.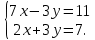
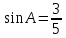 . Найдите AC.
. Найдите AC.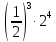 ; б) 7 + 2√5 - √20.
; б) 7 + 2√5 - √20.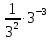 ; б) 5 - 3√7 + √63.
; б) 5 - 3√7 + √63.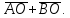
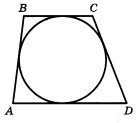 ешитеуравнение: 3х2 + 5х - 2 = 0.
ешитеуравнение: 3х2 + 5х - 2 = 0. ыполните действия:
ыполните действия: 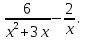
 ешите систему уравнений:
ешите систему уравнений: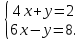
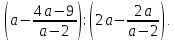
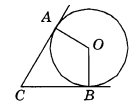 угол С величиной 79 вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB.
угол С величиной 79 вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB.