Лаба. Лабораторная работа №2. Прикладная информатика в нефтегазовой отрасли
 Скачать 34.24 Kb. Скачать 34.24 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Уфимский государственный нефтяной технический университет» Высшая школа информационных и социальных технологий Кафедра «Информационных технологий и математики» КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ Лабораторная работа №2 по дисциплине «Компьютерное моделирование» по направлению подготовки 09.03.03 Прикладная информация, профиль «Прикладная информатика в нефтегазовой отрасли» Выполнил: Студент гр. БНИ-19-01 Л.Р.Фазлыхаков Проверил: к.ф.-м.н. С.Н.Коледин Уфа, 2021 Задание 1: Составить и отладить программу определения площади фигуры методом МонтеКарло в соответствии с индивидуальным заданием. Вариант 11 Условия, ограничивающие фигуру: 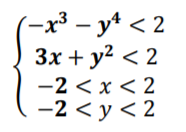 Контрольное значение St = 7,13684 Решение: function MK(n) k = 0; % Счётчик точек, упавших на фигуру st = 7.13684;% Истинное значение площади фигуры s0 = 16;% Площадь прямоугольника for i=0:n %генерируем точку с координатами х и у из указанного диапазона x = -2 + (2+2).*rand(1); y = -2 + (2+2).*rand(1); %проверяем условие на попадание внутрь фигуры if (-x^3 - y^4 < 2) && (3 * x + y^2 < 2) k = k + 1;%обновляем счётчик end end s = k * s0 / n; disp(strcat('Вычисленное значение площади: ', num2str(s))) sigma = abs(s - st)/st; disp(strcat('Истинное значение площади: ', num2str(st))) disp(strcat('Погрешность вычислений: ', num2str(sigma))) end >> MK(1000) Вычисленное значение площади:7.152 Истинное значение площади:7.1368 Погрешность вычислений:0.0021242 Задание 2: Вариант 11 Вычислить методом Монте-Карло определенный интеграл. Сравните результат со значением, полученным аналитическим путем при значениях N=10, 100, 1000, 10000, 100000, 1000000. Выразите относительную погрешность метода Монте-Карло при каждом значении N. Исходники к заданию 2: 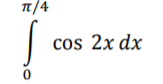 = 0,5 function MK() k = 0; % Счётчик точек, упавших на фигуру s0 = pi/4 * 1; % Площадь прямоугольника st = 0.5; % Истинное значение определенного интеграла for n = [10, 100, 1000, 10000, 100000, 1000000] % вектор с количеством итераций (или точек) for i=0:n %генерируем точку с координатами х и у из указанного диапазона x = 0 + (pi/4).*rand(1); y = 0 + (1).*rand(1); %проверяем условие на попадание внутрь фигуры if (cos(2 * x) <= pi/4) && (cos(2 * x) >= 0) k = k + 1; %обновляем счётчик end end s = k * s0 / n; disp('-------------------------------------------------------') disp(strcat('При количестве итераций == ', num2str(n))) disp(strcat('Вычисленное значение площади: ', num2str(s))) sigma = abs(s - st)/st; disp(strcat('Истинное значение площади: ', num2str(st))) disp(strcat('Погрешность вычислений: ', num2str(sigma))) end end При количестве итераций ==10 Вычисленное значение площади:0.62832 Истинное значение площади:0.5 Погрешность вычислений:0.25664 ------------------------------------------------------- При количестве итераций ==100 Вычисленное значение площади:0.47909 Истинное значение площади:0.5 Погрешность вычислений:0.041814 ------------------------------------------------------- При количестве итераций ==1000 Вычисленное значение площади:0.5003 Истинное значение площади:0.5 Погрешность вычислений:0.00059726 ------------------------------------------------------- При количестве итераций ==10000 Вычисленное значение площади:0.50423 Истинное значение площади:0.5 Погрешность вычислений:0.0084512 ------------------------------------------------------- При количестве итераций ==100000 Вычисленное значение площади:0.50172 Истинное значение площади:0.5 Погрешность вычислений:0.0034404 ------------------------------------------------------- При количестве итераций ==1000000 Вычисленное значение площади:0.50207 Истинное значение площади:0.5 Погрешность вычислений:0.0041378 |
