Индивилуальный подход. Применение индивидуального подхода в начальной школе Дьякова Софья Михайловна
 Скачать 194.74 Kb. Скачать 194.74 Kb.
|
|
Применение индивидуального подхода в начальной школе Дьякова Софья Михайловна учитель начальных классов Новосибирск 2020 Содержание Введение 3 Глава 1. Теоретические основы применения индивидуального подхода в начальной школе 5 1.1. Сущность и характеристика индивидуального подхода 5 1.2. Возможности применения индивидуального подхода на уроках математики в начальной школе 9 Глава 2. Экспериментальное исследование применения индивидуального подхода в начальной школе на уроках математики 18 2.1. Результаты констатирующего этапа эксперимента 18 2.2. Реализация индивидуального подхода на уроках математики в начальной школе 21 2.3. Эффективность реализации индивидуального подхода на уроках математики 27 Заключение 29 Список использованных источников 32 ВведениеПроблема индивидуального подхода в обучении детей имеет достаточно богатую историю. О необходимости учёта возрастных и индивидуальных особенностей развития детей в воспитании и обучении говорили Я.А. Каменский, И. Г. Песталоцци, А. Дистервег, Ж.-Ж. Руссо и другие. Большой вклад в педагогическое обоснование индивидуальной работы с детьми в учебно-воспитательном процессе внесли работы П. П. Блонского, А.В. Луначарского, А. П. Пинкевича, С. Т. Шацкого. Наиболее общие положения теории индивидуализации содержатся в пособиях Ю. К. Бабанского, М. А. Данилова, Б. П. Есипова, А. А. Кирсанова, Е. С. Рабунского, М. Н. Скаткина, И. Э. Унт и других. Индивидуальный подход в начальной школе предполагает учет индивидуальных различий учеников и, соответственно вариативность методов воспитания, обучения, особые формы организации учебного процесса. Успешность осуществления данного подхода напрямую зависит от знания учителем индивидуальных особенностей учащихся и от умения эти особенности постоянно изучать. В итоге, индивидуальный подход в обучении и воспитании в начальной школе означает действенное внимание к каждому младшему школьнику, его творческой индивидуальности в условиях классно-урочной системы и предполагает разумное сочетание фронтальных, групповых и индивидуальных форм занятий в начальной школе. Математические знания для ребенка служат средством интеллектуального развития, его познавательных и творческих способностей. В ходе математического развития у учащихся с задержкой психического развития формируются психические функции и процессы, совершенствуется наглядно-действенное, наглядно-образное и словесно-логическое мышление. Математика, бесспорно, является самым трудным для обучения детей в начальной школе (а также и иной) предметом, который требует наличия ряда способностей: умения анализировать и обобщать материал и мыслить отвлеченно, абстрактными категориями; гибкости мышления; наличия специфической математической памяти. Практические же приложения данной теории в работе начальной школы выражены не полностью. Таким образом, несмотря на сравнительно большое число работ об индивидуальном подходе, эта актуальная проблема продолжает оставаться малоразработанной. Объект исследования – индивидуальный подход. Предмет исследования – применение индивидуального подхода в начальной школе. Цель работы – изучить возможности применения индивидуального подхода в начальной школе. Задачи: изучить сущность индивидуального подхода; рассмотреть возможности применения индивидуального подхода на уроках математики в начальной школе; провести экспериментальное исследование применения индивидуального подхода в начальной школе на уроках математики. Гипотеза исследования: предполагается, что применение индивидуального подхода на уроках математики в начальной школе будет способствовать эффективному формированию вычислительных навыков младших школьников. Методы исследования: анализ теоретических источников; сравнение; обобщение; систематизация; тестирование; количественный и качественный анализ результатов. Структура работы. Исследование включает введение, двух главы, заключение и список использованных источников. Глава 1. Теоретические основы применения индивидуального подхода в начальной школе1.1. Сущность и характеристика индивидуального подходаВ психолого-педагогической науке отсутствует единообразное понимание понятий «индивидуальный подход» и «индивидуализация». Г. М. Коджаспирова индивидуальный подход характеризует как «осуществление педагогического процесса с учетом индивидуальных особенностей учащихся (темперамента, характера, способностей, склонностей мотивов, интересов и др.)» [14, с. 100]. Данный подход предполагает подбор и использование таких методов, приемов и форм обучения, которые будут способствовать достижению оптимального результата как в обучении, так и в воспитании. Идентичную позицию по отношению к индивидуальному подходу занимает и Т. М. Ковалева [12]. Индивидуальный подход направлен на усвоение единого содержания и не предполагает создания оптимальных условий для реализации потенциальных возможностей обучающегося, ориентирован только на те условия, которые способствуют усвоению и осознанию заданного программного материала. Интерес к индивидуализации возрастает, поскольку трансформировалась культурно-историческая среда, произошли изменения в межличностных и межгрупповых отношениях людей, изменилось отношение к обучающимся с объекта на субъект учебной деятельности, который стремится к самоопределению и самореализации. А. В. Петровский индивидуализацию связывает с одной из фаз на каждом возрастном этапе, при вхождении человека в новый социум, группу, коллектив [20]. В современных исследованиях отмечается, что ребенок поставлен в ситуацию разрозненных связей, на его сознание одновременно влияет поток бессвязной информации из разнообразных источников. Это определило качественные психологические, психофизиологические и личностные изменения ребенка [21]. Взрослое сообщество не успевает даже фиксировать, а тем более анализировать изменения в социуме и в личности подрастающего поколения. Безусловно, необходимо искать новые решения в организации учебного процесса, при которой мобилизуются возможности любого ребенка. Поскольку «развитие личности – это единый процесс социализации, когда ребенок осваивает социальный опыт, и индивидуализации, когда он выражает собственную позицию, противопоставляет себя другим, проявляет самостоятельность путем установления все более широких отношений, где он сам себя проверяет. Основная образовательная программа состоит их двух частей: обязательная часть и часть, формируемая участниками образовательного процесса. Соотношение этих частей разное в зависимости от уровня образования: на этапе начального общего образования 80% к 20%, на этапе основного общего образования 70% к 30%. За счет реализации части, формируемой участниками образовательного процесса, при адекватной организации, на основе фиксации познавательного интереса и разработке индивидуального образовательного маршрута и индивидуальной образовательной траектории, в современной практике можно создать условия для реализации способностей каждого обучающегося. В. Б. Лебединцев трактует индивидуализацию как организацию учебного процесса, при которой выбор способов, приемов, темпов обучения осуществляется сообразно индивидуальным особенностям и образовательным потребностям обучающихся. Интерес к подобной организации процесса возник в связи с неразрешимым противоречием между индивидуальным характером усвоения содержания образования и преобладанием фронтальных форм при организации обучения. В. Б. Лебединцев выделяет три группы форм индивидуализации в соответствии с уровнями структурной организации обучения: на уровне деятельности обучающихся: индивидуальные задания; разноуровневые дидактические материалы; модульные программы; на уровне учебного коллектива: внутренняя дифференциация – разделение на микрогруппы; на уровне институциональной системы обучения: аудиторные занятия: гомогенные классы по способностям и интересам; выбор обучающимися учебных курсов из вариативных учебных планов; разноуровневые задания: нормативный, компетентный и творческий; за рамками обязательных аудиторных занятий: самостоятельная работа, семейное воспитание, репетиторство; индивидуальные занятия с одаренными детьми; индивидуальные проекты; индивидуальные образовательные маршруты; индивидуальные образовательные программы [16]. Автор акцентирует внимание на необходимости использования не только фронтальных форм организации обучения. Поскольку тогда затруднена полноценная индивидуализация. При доминировании фронтальной формы работы только на уровне нормы педагоги осуществляют положительное стимулирование при изучении материала. Однако если ребенок отстающий – он не успевает усваивать предложенный учебный материал, а если опережает в развитии – ему не предоставляется возможность реализовать свои способности [16]. В. Б. Лебединцев характеризует три группы педагогических условий, необходимых для индивидуализации: процессуальные условия: персональный темп прохождения материала; завершённость усвоения учебного материала на каждом этапе учения; использование на одном занятии разных форм обучения; подвижный состав учебных групп; многообразие управленческих процессов, использование несколько обучающих программ, адресованных разным обучающимся; сотрудничество участников коллектива; содержательные условия: формирование надпредметных способов деятельности; разнообразие образовательных ситуаций и форм дидактического материала; многообразие маршрутов освоения образовательной области; управленческие условия: включение с совместную рефлексию; учет достигнутого уровня, определение динамики изменений; постановка диагностических дидактических задач, через действия, которые можно опознать; готовность учителей к индивидуализации обучения [16]. Индивидуализацию Л. В. Байбородова и Т. В. Бурлакова характеризуют как «динамический, интериоризированный личностью процесс взаимодействия, который адекватен как индивидуально-образовательному потенциалу обучающегося, так и системе социальных ценностей, требований и целей; способствует позитивному изменению внутреннего мира человека, обеспечивает овладение способами познания мира и себя для самореализации в образовании и жизни» [4]. Результатом индивидуализации является: осознанный выбор своей образовательной траектории; осознание и использование ресурсов своих и окружающей среды; ответственность за свой выбор. Л. В. Байбородова и Т. В. Бурлакова выделяют особенности индивидуализации: посредством освоения образовательных ценностей и опыта обучающиеся осознают себя; целенаправленность; невозможна без самоанализа, мотивации и рефлексии; способствует развитию своих способностей – с одной стороны, с другой – активизирует желание отдавать приобретенные знания. Авторы акцентируют внимание на двух сторонах индивидуализации: внутренней (процесс качественных изменений человека, направлен на реализацию уникальной сущности, результат – рефлексивные умения) и внешней (многообразие полноценных привлекательных вариантов образовательной деятельности – вариативность). Ими установлено, что осуществление только внешней стороны не приводит к реализации у обучающегося потребности в самоопределении. По мере развития обучающегося возрастает роль внутренней стороны индивидуализации [4]. Анализ психолого-педагогической литературы позволяет утверждать, что общим для всех толкований является акцент на системе воспитания и обучения, при которой создаются условия для успешного становления индивидуальности человека. Индивидуализация предполагает поддержку и сопровождение молодого поколения в процессе обучения, воспитания и развития, а именно: постановка целей и задач, стимулирование, актуализация и активизация на этапе реализации, оценка достигнутых результатов по разным основаниям (для себя, для коллектива, для социума), реализация своего потенциала. 1.2. Возможности применения индивидуального подхода на уроках математики в начальной школеМатематические знания служат средством интеллектуального развития ребенка, его познавательных и творческих способностей. В ходе математического развития у младших школьников формируются психические функции и процессы, совершенствуется наглядно-действенное, наглядно-образное и словесно-логическое мышление. Математическая подготовка дает младшему школьнику возможность правильно воспринимать окружающий мир, ориентироваться в нем, выполнять элементарные арифметические действия в игровой, трудовой, конструктивной, изобразительной, бытовой деятельности. Уже на начальном этапе обучения детей счёту, арифметическим действиям по различным причинам могут возникать трудности в овладении счётными навыками, среди которых выделяется специфическое стойкое нарушение в овладении счетными операциями − дискалькулия. В исследованиях, посвящённых изучению дискалькулии, подчёркивается сложность причин и механизмов данного нарушения, его стойкость и трудность преодоления. К имеющимся трудностям присоединяются дополнительные проблемы, которые отрицательно отражаются на личности ребёнка и на школьной жизни в целом [1, с. 112]. Математика является, наиболее трудным для обучения детей предметом, который требует наличия определенных способностей: умения анализировать и обобщать материал; умения мыслить отвлеченно, абстрактными категориями; гибкости мышления; наличия специфической математической памяти. Особенностью математики является высокий уровень абстракции, что обуславливает наличие своего символического языка, своего способа обоснования. Отсюда ее составляющие в начальном авторском курсе математики: арифметика (с элементами алгебры); образная геометрия; элементы комбинаторики; элементы логики. Каждая из составляющих, с одной стороны, имеет самостоятельное значение и логику развертывания, а с другой, - изучается во взаимосвязи с другими, что способствует созданию у школьников более полного представления о математике, ее пониманию и культурному освоению [10, с. 19]. Выбор составляющих линий курса математики определяется как необходимостью пропедевтики соответствующих разделов математики. Изучение геометрии в большей степени связано с развитием пространственного мышления; изучение арифметики и элементов логики требует большей алгоритмизации и формализации мыслительной деятельности; изучение комбинаторики способствует развитию вариативности, критичности мышления. Ведущие линии (арифметическая и геометрическая) равноправны, они закладывают основу изучения двух математических областей и способствуют развитию разных психических структур. Две другие линии в большей степени выполняют пропедевтические функции: готовят учащихся к усвоению в основной школе таких разделов, как «Логика» и «Комбинаторика» и к изучению арифметического, алгебраического и геометрического материала. Осознание ребенком ценности математического знания (для изучения других предметов, для собственного развития, в качестве интеллектуального ресурса решения жизненных задач) достигается через привлечение знаний из других школьных дисциплин, показ зависимости выбора решения рассматриваемой ситуации (задачи) от конкретных условий, выбор наиболее рационального способа решения задачи и др. В результате развивается способность применять математические знания в новой жизненной ситуации, что является признаком присвоения специфических для математики способов деятельности. Данная способность обеспечивает приобретение новых знаний, их преобразование и применение, способствует формированию современной научной картины мира. Для курса математики основным является системно-деятельностный подход, согласно которому обучение математике организуется как учебная деятельность школьников на математическом содержании [8, с. 277]. При обучении математике необходимо учитывать специфические черты науки математики: оперирование абстракциями высокого уровня и наличие собственного языка, отличного от естественного. Поэтому реализация принципов обучения, сформулированных в курсе обучения математике, имеет свои особенности. Принцип диалогизации при обучении математике реализуется с двух позиций: а) становление и развитие математической речи, на базе которой возможна равноправность участников диалога в поиске решения, стремление к взаимопониманию, порождению смысла, а не получение заранее известной суммы знаний и б) развитие коммуникативных умений. В начальных классах ученики знакомятся с основными элементами алфавита школьной математики, включающего различные математические языки (знаковые системы): естественный язык (слова родного языка, научные термины), графический язык (схемы, чертежи), символический язык (логико-математические символы). Усвоение каждого из названных языков и умение переводить текст с одного языка на другой способствуют пониманию математики, являясь признаками математической культуры. Поэтому в текстах учебников математики предлагаются разного рода памятки, которые являются образцами математической речи; специальные задания, которые способствуют усвоению основ математического, графического, символического языков, овладению правилами построения из них различных конструкций, выявлению их содержательного смысла [18]. Для развития коммуникативных умений важно использование различных форм организации учебного процесса: дискуссии, работа в паре постоянного состава, в паре сменного состава, КСО, работа над проектом, проведение мини исследования и др. В процесс обучения математике принцип вариативности реализуется через учебную и психологическую дифференциацию. С позиций учебной дифференциации вариативность относится к содержанию заданий (задания отличаются по степени сложности, по объему), самостоятельности выполнения, методам и средствам обучения. С позиций психологической дифференциации задания в учебнике отличаются но способу восприятия и их выполнения - для слухового (аудиального) восприятия, зрительного (визуального), двигательного (кинестетического) [8, с. 278]. Осуществляется учет всех составляющих субъектного опыта ребенка как ценности и базовой ступени присвоения общественноисторического опыта в области математики на всех этапах обучения, как условия понимания себя и других, выявление и окультуривание субъектного опыта ребенка. Начальный этап изучения математики в школе рассматривается как базовый в процессе математического развития школьников, поскольку именно в этот период математика впервые становится предметом систематического изучения, закладывается основа для понимания математических абстракций, поэтому особую значимость приобретает принцип преемственности и перспективности в обучении. Данный принцип реализуется в содержательном и в развивающем аспектах. Содержательный аспект направлен на расширение и углубление знаний и умений, их поступательное развертывание. Изучение курса математики организовано по спирали: вопросы программы рассматриваются неоднократно, каждый раз на более высоком уровне. Содержание учебного материала представляет собой не набор отдельных сведений из разных областей математики, а взаимосвязанную последовательность тем. Развивающий аспект рассматриваемого принципа включает создание условий для установления самим учеником взаимосвязи между старым и новым опытом, что способствует преобразованию отдельных умений ученика в новое интегративное умение. К таким условиям относятся выполнение заданий рефлексивного характера, обеспечивающих осознание учениками причин возникающих трудностей, заданий не только из зоны ближайшего, но перспективного развития («будущая задача»), поиск и обсуждение ошибок, поиск условий применимости правила и т.д. Кроме того, ребенок приходит в школу, обладая определенным жизненным опытом, начальными математическими знаниями, которые носят житейский характер. Учет субъектного опыта, способа восприятия мира, использование разных каналов получения информации при выполнении одних и тех же заданий в процессе обучения математике способствуют преобразованию житейских понятий в теоретическое знание, его обогащение. В связи с высоким уровнем абстракции математического знания специфическим для обучения математики является принцип приоритета понимания над запоминанием, который тесно связан с принципом преемственности и перспективности. Благодаря конкретным примерам ребенок связывает новое математическое знание с некоторыми фактами, уже имеющимися в его опыте, т.е. переводит научное понятие на собственный язык (вводит в свой субъектный опыт). Рассмотрение перцептивного пространства в процессе изучения математики позволяет создать базу (преимущественно на уровне обобщенных представлений) для ознакомления ученика с наукой математикой. Необходимость учёта индивидуальных особенностей учащихся в процессе обучения является приоритетным в педагогической психологии, дидактике и методике. Все дети разные, поэтому каждый учитель знает, что на уроке необходим индивидуальный подход к каждому ученику. Именно тогда создаются необходимые условия для максимально полного всестороннего развития ребёнка, возникает комфортная для каждого учащегося образовательная среда, находят своё решение многие проблемы неуспевающих школьников [13; 17]. Способствовать достижению младшими школьника как метапредметных, так и предметных результатов при изучении математики могут электронные образовательные ресурсы [7, с. 87]. Поскольку младшие школьники имеют различный уровень подготовки по математике, неодинаковые успехи в усвоении знаний, умений и навыков, проявляют различный интерес к учебному предмету, то реализация индивидуального подхода на уроках математики осуществляется через средства обучения. В качестве основных средств обучения математики выступают: методические комплекты, карточки, самостоятельные работы, тестовые задания [11, с. 84]. Специально отбираемые задания должны быть ориентированы на: постепенное усложнение материала, поэтапное увеличение объёма работы, повышение уровня самостоятельности учащегося, обучение способам рассуждения с учётом принципа вариативности задач формирование беглости мыслей, оригинальность, гибкость ума, любознательность, умение выдвигать и разрабатывать гипотезы. Одним из эффективных средств обучения математике в начальной школе является применение средств наглядности, поскольку одной из основных задач обучения математике детей с задержкой психического развития является развитие навыков отвлеченного мышления. Однако оно не может возникнуть без конкретного образа. Благодаря средствам наглядности формируются конкретные представления. С помощью наглядности развивается сенсорный опыт учащихся, а это есть предпосылка и условие формирования наглядно-образного мышления. Сформированные представления служат базой для развития абстрактного мышления [19, с. 78]. Дети младшего школьного возраста легко усваивают лишь то, что они могут непосредственно воспринять, и чем больше анализаторов будет участвовать в этом восприятии, тем легче и прочнее будет усвоение. Поэтому в начальных классах наглядные пособия играют особенно большую роль. В учебном процессе учитель демонстрирует самые разнообразные виды наглядных пособий: предметы (книги, конверты, карандаши, открытки и т.д.), модели предметов, таблицы, природный материал. Многие из этих пособий могут быть использованы на уроках как раздаточный материал. К современному периоду относится выход программы и учебников математики для 1-4 классов в УМК «Диалог», в авторский коллектив которых входят доценты кафедры НЕМО О.А. Ивашова и Е.Е. Останина [8]. Одной из особенностей курса математики является использование и уровневой, и психологической дифференциации, которые являются основой индивидуального подхода. В программе в 2-х уровнях сформулированы требования к предметным результатам обучения математике не только к окончанию начальной школы (как ориентирует ФГОС НОО), но и концу каждого учебного года. Содержание 2-го уровня является ориентиром на следующий учебный год, работу с ним учитель ведет в течение всего года, но не требует его усвоения от всех учащихся. Кроме того, в программе охарактеризованы 4 уровня достижения метапредметных результатов обучения (низкий, опорный, повышенный, перспективный). В учебниках математики (например, [18]) уровневая дифференциация реализуется через задания, отличающиеся по степени сложности, по объему, по самостоятельности выполнения. Ученику периодически предоставляется право выбора задания, средства и способа выполнения и/или контроля. В учебниках имеется постоянная рубрика «Выбери, выполни, поделись с другими». Важной особенностью учебников математики является реализация идеи психологической дифференциации. Особенность разработанного авторами курса состоит в том, что в учебниках учитываются разные виды восприятия и переработки информации: слуховое (аудиальное) восприятие, зрительное (визуальное), двигательное (кинестетическое). Для этого предусмотрены задания со специальными значками, что дает возможность каждому ученику воспринять и понять новую математическую информацию. На этапе ознакомления новый материал связан с какими-то реальными практическими действиями, представлен зрительно, проговорен вслух каждым учеником. Например, при решении задачи «Дети посадили 12 кустов клубники по 3 куста в каждом ряду. Сколько рядов клубники получилось?» учащиеся практически действуют с моделями чисел (раскладывают палочки по 3), видят, как эти действия представлены на рисунке (схематический чертеж), как они преобразуются в записи, в словесные формулировки. Эта идея была представлена авторами в учебниках математики уже в 2009 г. (издательство «Дрофа»). К современному периоду относится разработка О.А. Граничиной и О.А. Ивашовой идей и математических материалов Всероссийской дистанционной метапредметной олимпиады для младших школьников «Новые знания» [5], направленной на диагностику сформированности универсальных учебных действий (УУД). Первой особенностью олимпиады (реализованной Центром независимых педагогических измерений «ЭффектТест»), является ее метапредметный характер. Индивидуально-дифференцированный подход к младшим школьникам был связан с достижением не столько предметных результатов, сколько с формированием познавательных УУД (проверялось на четырех предметных областях: математика, русский язык, окружающий мир, литературное чтение). Вторая особенность олимпиады – дистанционная форма, которая расширила возможности работы с одаренными детьми, живущими в разных уголках России, в том числе удаленных (в первой олимпиаде участвовало около 109 000 младших школьников). Подводя итог, можно отметить, что методисты-математики на протяжении десятилетий, отвечая велениям времени, развивали идеи внешней и внутренней дифференциации в обучении младших школьников. Важно, что методические идеи были не только апробированы в научных исследованиях (преподавателей, студентов, магистрантов и учителей), но и реализованы в учебниках математики для массовой начальной школы, в учебных пособиях для учащихся, в электронных образовательных ресурсах, в том числе в дистанционных олимпиадах. Большое внимание в течение многих лет уделялось работе с детьми, интересующимися математикой. Глава 2. Экспериментальное исследование применения индивидуального подхода в начальной школе на уроках математики2.1. Результаты констатирующего этапа экспериментаЭкспериментальное исследование проводилось на базе МБОУ СОШ № 90 с углубленным изучением предметов художественно-эстетического цикла. В исследовании принимали участие младшие школьники 2-го класса. Цель констатирующего этапа – определить исходный уровень сформированности вычислительных навыков у детей младшего школьного возраста.    После проведения констатирующего исследования было установлено, что у пятерых учащихся класса низкий уровень сформированности знаний, у тринадцати учащихся – средний уровень и только семерых вычислительный навык сформирован на высоком уровне (рис. 1). 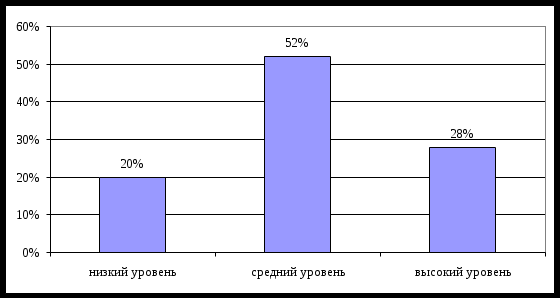 Рисунок 1 – Результаты исследования исходного уровня вычислительных навыков на констатирующем этапеИз рис. 1 можно сделать вывод, что детей с низким уровнем сформированности вычислительных навыков – всего 20 %, со среднем уровнем – 52 %, а с высоким составляет – 28%. Таким образом, на основе полученных результатов можно сделать вывод о том, что во 2 классе сформированность вычислительных навыков на среднем уровне. Большинство учащихся допускают в вычислениях ошибки, связанные со сложением и вычитанием с переходом через разряд, а так же не всегда могут объяснить решение примера. Осознанность вычислительных действий сформирована в достаточной степени – большинство учащихся данного класса могут объяснить выбор операций при решении примера, так же почти все дети могут сравнивать выражения с одинаковым слагаемым, уменьшаемым или вычитаемым не вычисляя их значение. Всего шестеро учащихся класса выполняют вычисления правильно, без ошибок, что говорит о необходимости совершенствования вычислительных навыков. Поэтому необходимо разработать совокупность заданий, направленных на совершенствование и необходимых вычислительных навыков, и включить их в учебный процесс 2 класса. 2.2. Реализация индивидуального подхода на уроках математики в начальной школеНа основе результатов, полученных в ходе констатирующего эксперимента, была разработана совокупность заданий, направленных на улучшение качества сформированных знаний и увеличение количества усвоенных вычислительных приемов. Задания включались в уроки математики на различных этапах их проведения (таблица 1).
|
| 1 | 2 | 3 |
| Свойства сложения | Нахождение значений выражений с элементом занимательности | Сложение двузначных чисел с переходом через разряд. Сложение двузначных и трехзначных чисел без перехода через разряд |
| Вычитание числа из суммы | Задания с многовариантными решениями с элементом занимательности | Сложение и вычитание двузначных чисел с переходом через разряд |
Задания давались детям на основе индивидуального подхода, то есть с учетом имеющихся у конкретного школьника знаний и умений.
Приведем примеры включения заданий в уроки математики.
На уроке по теме «Обратные операции» на этапе закрепления предлагалось учащимся следующее задание:
Найдите значение выражений.
42 + 30 57 + 12 67 + 19 24 + 78
К каждому равенству напишите все возможные равенства с обратным действием. Какое это действие?
Выполняя такое задание, у детей закрепляется вычислительный навык сложения с переходом через разряд и без перехода. Так же формируется осознанность, т.к. при выполнении такого задания, детям нужно записать выражения с обратными действиями, что требует от детей понимания взаимосвязи между компонентами и результатом действий сложения и вычитания.
На уроке по теме «Сложение трехзначных чисел с переходом через разряд» на этапе актуализации знаний предлагается учащимся следующее задание:
Найдите значение выражений:
34 + 12 84 + 15 56 + 27 67 + 32
48 – 29 23 – 14 92 – 35 75 – 38
Разделите данные выражения на две группы. По какому признаку вы разделили данные выражения?
При разделении данных выражений, учащиеся будут выделять вычислительные приемы, на которых они основаны. При этом они повторяют приемы сложения и вычитания с переходом через разряд и без перехода и осознают правила, на которых они основаны. Выполняя такие задания, дети определяют, какие из них относятся к группе вычислений с переходом через разряд, а какие без перехода. Такие задания подготавливают детей к более сложной работе (сложение трехзначных чисел с переходом через разряд).
На уроке по теме «Виды алгоритмов» на этапе изучения нового материала учитель включает следующие задания:
Пользуясь алгоритмом сложения двузначных чисел, вычисли суммы:
25 + 32 + 14 16 + 28 + 50
43 + 34 + 70 81 + 39 + 87
Выполняя подобное задание, дети отрабатывают прием сложения двузначных чисел с переходом через разряд и без перехода. Действуя строго по алгоритму, дети более прочно усваивают данные приемы, т.к. неверные вычисления приводят к неверному решению алгоритма, и значит решать придется сначала. Многократное повторение вычислительных действий способствует более прочному усвоению вычислительного приема.
На уроке по теме «Свойства сложения» на этапе работы по новой теме учитель предлагает детям найти равные выражения и вычислить их значение удобным способом.
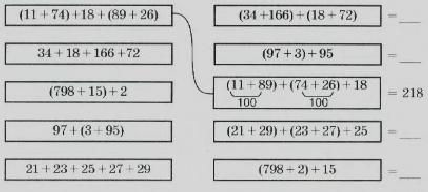
Рисунок 2 – Способы решения заданий
Какие свойства сложения были использованы для упрощения вычислений?
При работе с подобным заданием перед детьми стоит не только задача вычислить значение выражений, но и упростить процесс вычислений, используя свойства сложений, которые лежат в основе вычислительных приемов сложения с переходом через разряд и без перехода. Дети повторяют и закрепляют эти приемы. В результате многократного использования данных приемов, дети более прочно и осознано усваивают их.
На уроке по теме «Вычитание числа из суммы» на этапе закрепления учитель может предложить детям поиграть в «Лабиринт». Детям предлагается найти все возможные варианты «выхода» из лабиринта (рис. 3).
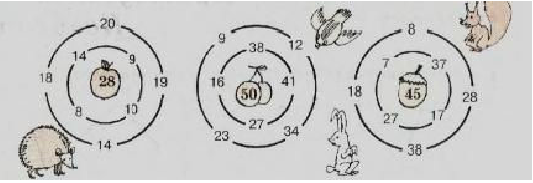
Рисунок 3 – «Лабиринт»
Выполнение этого задания требует от детей внимательных и осознанных вычислений. Так как решений может быть несколько, детям предстоит не один раз пройти «лабиринты», находя то верные, то неверные пути, что приводит к закреплению приемов сложения и вычитания с переходом через разряд и без перехода.
Для повышения уровня сложности задания учебника на его основе:
задавались учащимся дополнительные вопросы, например, направленные на выявление закономерностей;
предлагалось учащимся продолжить выявленную закономерность или самим составить аналогичные задания.
Например, ученикам, правильно и быстрее других вычислившим значения выражений, дается дополнительное задание: «Обозначь числа квадратами и запиши схему, по которой составлены все выражения в этом столбике, придумай свое выражение по схеме, вычисли его значение».
Особое внимание уделялось тому, чтобы все ученики выполняли упражнения по одной и той же теме.
Например, при выполнении упражнений давались задания на выбор:
реши два любых примера;
выбери и реши те примеры, где неизвестное находится вычитанием;
выбери и реши те примеры, где вычитаемое будет однозначным числом.
При этом важным стало, кто выбирает уровень задания: учитель для ученика или сам ребенок. В процессе формирующего этапа мы апробировали идею свободного выбора, когда учащийся сам решает, какого уровня задание он выполняет в данный момент. Были выделены условия для выбора задания учеником в соответствии с его возможностями – у него должны быть сформированы: адекватная самооценка, умение работать самостоятельно, желание работать активно, на пределе своих сил.
Сначала сложность заданий учителю обсуждались с детьми, чтобы помочь им осуществить выбор задания. Затем учитель оценивает ее в очках, например: «Если выберешь готовые примеры, за каждое верно решенный начисляй себе 4 очка, если будешь сам заканчивать составление и решать, то за каждый пример – 7 очков».
Включение подобных заданий в уроки математики, на разных этапах их проведения, позволили сформировать у учащихся более прочные и осознанные вычислительные навыки. Частое повторение одного и того же вычислительного приема способствовало улучшению качества и количества сформированных вычислительных приемов.
С целью наибольшей занятости учащихся на уроке необходимо постоянно использовать индивидуальные формы работы. Ведь именно самостоятельная деятельность учащихся занимает значительное место в преподавании математики. Для большей эффективности самостоятельная деятельность в учебном процессе должна носить творческий характер. Тогда она способствует сознательному усвоению и переносу знаний, умений и навыков в новые ситуации, что ведёт к развитию познавательной самостоятельности и активности. В связи с этим необходимо на уроке использовать задания для самостоятельной деятельности творческого характера, которые нацелены на формирование у младших школьников вычислительных навыков.
Каждый ученик получает индивидуальное задание. Чаще всего это задания-карточки. Индивидуальные задания особенно важны для школьников с негативным отношением к учебе так учитель исходит из способностей учащегося и дает посильное задание. Такого рода задания требуют опоры на ранее приобретённые знания и умения. Учащиеся должны научиться применять эти знания в новых ситуациях. Получив карточку с разноуровневыми заданиями, ученик выбирает задание по уровню своих умственных способностей. Справившись со своим заданием, школьник может перейти к следующему заданию.
Развитию вычислительной культуры у младших школьников на уроках математики способствуют тесты. Тесты обладают целым рядом положительных характеристик: быстрота проверки выполненной работы, оценка достаточно большого количества учащихся, возможности проверки усвоения теоретического материала, проверка большого объёма материала малыми порциями, объективность оценки результатов выполненной работы.
В начальных классах лучше всего использовать тесты с выбором одного верного ответа, так как они наиболее доступны младшим школьникам. При составлении тестов важно учитывать типичные ошибки учащихся. Такого вида тесты помогают учителю получить информацию о качестве формирования вычислительных навыков.
2.3. Эффективность реализации индивидуального подхода на уроках математики
Для проверки эффективности формирующего этапа эксперимента был проведен контрольный этап исследования.
После проведения тестирования были получены результаты, которые приведены на рисунке 4.
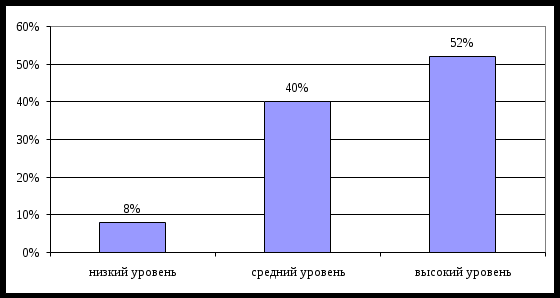
Рисунок 4 – Результаты исследования уровня вычислительных навыков на контрольном этапе
Из диаграммы следует, что детей с низким уровнем сформированности вычислительных навыков – 8 %, со среднем уровнем – 40%, с высоким – 52%.
Сравнительные результаты исследования вычислительных навыков на разных этапах экспериментальной работы представлены на рисунке 5.
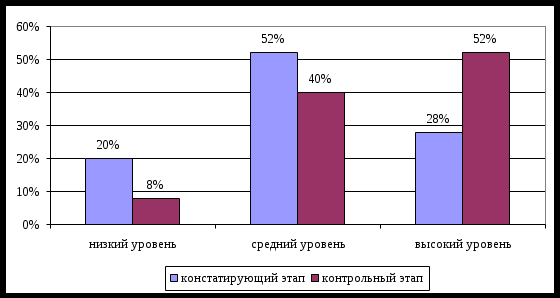
Рисунок 5 – Результаты исследования уровня вычислительных навыков на разных этапах экспериментальной работы
Анализ полученных данных свидетельствует о том, что среди второклассников снизилось количество учащихся с низким уровнем вычислительных навыков (с 20% до 8%) и увеличилось количество учащихся с высокий уровнем сформированности вычислительных навыков (с 28% до 52%).
Следовательно, разработанная и проведенная работа по формированию вычислительных навыков на основе индивидуального подхода оказалась эффективной.
Таким образом, можно сделать вывод, о необходимости применения принципа индивидуального подхода на уроках математики при формировании вычислительных навыков у младших школьников. При этом важно преподать учебный материал максимально понятно каждому ребенку. Необходима непрерывная целенаправленная работа педагога над планированием предстоящего урока математики, постоянное расширение и углубление знаний.
Заключение
В начальных классах ученики знакомятся с основными элементами алфавита школьной математики, включающего различные математические языки (знаковые системы): естественный язык (слова родного языка, научные термины), графический язык (схемы, чертежи), символический язык (логико-математические символы). Усвоение каждого из названных языков и умение переводить текст с одного языка на другой способствуют пониманию математики, являясь признаками математической культуры.
Индивидуальный подход направлен на усвоение единого содержания и не предполагает создания оптимальных условий для реализации потенциальных возможностей обучающегося, ориентирован только на те условия, которые способствуют усвоению и осознанию заданного программного материала. Результатом индивидуализации является: осознанный выбор своей образовательной траектории; осознание и использование ресурсов своих и окружающей среды; ответственность за свой выбор. Индивидуализация предполагает поддержку и сопровождение молодого поколения в процессе обучения, воспитания и развития, а именно: постановка целей и задач, стимулирование, актуализация и активизация на этапе реализации, оценка достигнутых результатов по разным основаниям (для себя, для коллектива, для социума), реализация своего потенциала.
Поскольку младшие школьники имеют различный уровень подготовки по математике, неодинаковые успехи в усвоении знаний, умений и навыков, проявляют различный интерес к учебному предмету, то реализация индивидуального подхода на уроках математики осуществляется через средства обучения. В качестве основных средств обучения математики выступают: методические комплекты, карточки, самостоятельные работы, тестовые задания. В комплексе обучения математики младших школьников особое место принадлежит индивидуальному подходу. В работах отечественных педагогов и психологов обоснована необходимость индивидуализации обучения с целью создания максимально благоприятных условий для развития индивидуально-психологических особенностей детей.
Экспериментальное исследование проводилось на базе МБОУ СОШ № 90 с углубленным изучением предметов художественно-эстетического цикла. В исследовании принимали участие младшие школьники 2-го класса.
Цель констатирующего этапа – определить исходный уровень сформированности вычислительных навыков у детей младшего школьного возраста. Диагностика показала, что детей с низким уровнем сформированности вычислительных навыков всего 20 %, со среднем уровнем – 52 %, а с высоким – 28%.
На основе результатов, полученных в ходе констатирующего эксперимента, были разработаны задания, которые направлены на улучшение качества сформированных знаний и увеличение количества усвоенных вычислительных приемов. Это задания давались детям на основе индивидуального подхода, то есть с учетом имеющихся у конкретного школьника знаний и умений. Так, для повышения уровня сложности задания учебника на его основе: задавались учащимся дополнительные вопросы, например, направленные на выявление закономерностей; предлагалось учащимся продолжить выявленную закономерность или самим составить аналогичные задания.
Для проверки эффективности формирующего этапа эксперимента был проведен контрольный этап исследования. Анализ полученных данных свидетельствует о том, что среди второклассников снизилось количество учащихся с низким уровнем вычислительных навыков (с 20% до 8%) и увеличилось количество учащихся с высокий уровнем сформированности вычислительных навыков (с 28% до 52%).
Таким образом, поставленные задачи были решены:
изучена сущность индивидуального подхода;
рассмотрены возможности применения индивидуального подхода на уроках математики в начальной школе;
проведено экспериментальное исследование применения индивидуального подхода в начальной школе на уроках математики.
Цель работы – «изучить возможности применения индивидуального подхода в начальной школе» можно считать достигнутой.
Список использованных источников
Агаева, И.Б. Особенности коррекционно-педагогической работы по профилактике вербальной дискалькулии у детей с ограниченными возможностями здоровья / И.Б. Агаева, С.Ю. Кондратьева // Общество: социология, психология, педагогика. – 2017. – № 1. – С. 112-116.
Александрова, Т.С. Методика развития математической деятельности младших школьников / Т.С. Александрова // Мир науки. – 2016. – Т. 4. – № 4. – С. 1.
Александрова, Т.С. Модель развития математической деятельности младших школьников / Т.С. Александрова // Университетский комплекс как региональный центр образования, науки и культуры: Материалы Всероссийской научно-методической конференции. – 2016. – С. 2220-2227.
Байбородова, Л. В. Индивидуализация образовательного процесса в школе / Л.В. Байбородова. – Ярославль: Изд-во ЯГПУ, 2011. – 281 с.
Граничина, О.А. Всероссийская дистанционная метапредметная олимпиада для младших школьников: новый подход к диагностике УУД / О.А. Граничина, О.А. Ивашова, Л.В. Савельева, М.П. Воюшина, Л.В. Симонова, Т.В. Зинченко, С.А. Кислинская // Герценовские чтения. Начальное образование. – 2015. – №2. – С. 9-15.
Ивашова, О.А. Вычислительная культура младших школьников / О.А. Ивашова // Начальная школа. – 2017. – № 2. – С. 44-48.
Ивашова, О.А. Использование электронных ресурсов для функциональной пропедевтики в начальной школе / О.А. Ивашова, Т.Д. Крюкова // Герценовские чтения. Начальное образование. – 2016. – Т. 7. – № 2. – С. 86-96.
Ивашова, О.А. Курс математики для начальной школы в системе «Диалог» / О.А. Ивашова, Н.С. Подходова, Е.Е. Останина // Герценовские чтения. Начальное образование. – 2013. – Т.4. Вып. 2. – С. 274-282.
Ивашова, О.А. Особенности учебников «Математика» для 1-4 классов в УМК «Диалог» / О.А. Ивашова, Н.С. Подходова, Е.Е. Останина // Образование в поликультурном обществе: сб. ст. Вып. 1. – СПб: Астерион, 2013. – С. 121-128.
Ивашова, О.А. Применение исследовательских заданий в занимательной форме для становления вычислительной культуры школьников / О.А. Ивашова // Начальная школа. – 2009. – № 8. – С. 19-25.
Игнатченко, С.Ю. Использование средств обучения математике при реализации индивидуального подхода в начальной школе / С.Ю. Игнатченко, А.М. Масленкина // Актуальные проблемы гуманитарных и естественных наук. – 2016. – № 12-6. – С. 84.
Ковалева, Т. М. Профессия «тьютор» / Т.М. Ковалева. – М.-Тверь: СФК-офис. – 246 с.
Ковтуняк, Н.Б. Индивидуальный подход в процессе формирования вычислительных навыков у младших школьников / Н.Б. Ковтуняк // Духовная ситуация времени. Россия XXI век. – 2019. – № 3 (18). – С. 46-48.
Коджаспирова, Г. М., Словарь по педагогике / Г.М. Коджаспирова, А. Ю. Коджаспиров. – М.: ИКЦ МарТ, 2005. – 448 с.
Куценкова, Т.С. Развитие математической деятельности младших школьников в условиях введения ФГОС / Т.С. Куценкова // Вестник Оренбургского государственного университета. – 2011. – № 16 (135). – С. 479-481.
Лебединцев, В. Б. Проблема индивидуализации обучения в общеобразовательной школе / В.Б. Лебединцев // Инновации в образовании. – 2013. – № 5. – С. 35-47.
Леонтьев, А.Н. Проблемы развития психики ребенка / А.Н. Леонтьев. – М.: ВЛАДОС, 2002. – 225 с.
Математика. 1 кл.: в 2 ч. Ч. 1.: учебник / О.А. Ивашова, Н.С. Подходова, В.М. Туркина, Е.Е. Останина; под ред. О.А. Ивашовой. – М.: Дрофа, 2014. – 158 с.
Отрубина Я.А. Индивидуальный подход в обучении математике младших школьников / Я.А. Отрубина // Современные проблемы естественно-математического образования младших школьников в рамках реализации стандартов второго поколения сборник научных статей второй интернет-конференции. ЯГПУ им. К.Д. Ушинского; под науч. ред. И.В. Налимовой, С.В. Жарова. – 2015. – С. 78.
Петровский, А. В. Психология о каждом из нас / А.В. Петровский. – М., 1992. – 354 с.
Полякова, Л.В. Индивидуализация и индивидуальный подход в образовании / Л.В. Полякова // Актуальные вопросы гуманитарных наук: теория, методика, практика К 20-летию кафедры методики преподавания истории, обществознания и права: Сборник научных статей. Под редакцией А.А. Сорокина. – 2019. – С. 483-493.
Селькина, Л.В. Механизмы достижения личностных результатов в процессе обучения математике / Л.В. Селькина // Начальная школа. – 2014. – №4. – С. 40-46.

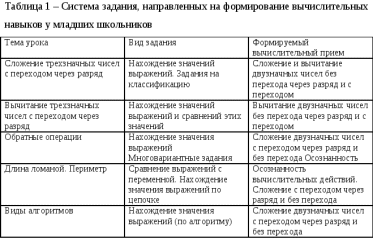 Продолжение таблицы 1
Продолжение таблицы 1