НПК по математике. НПК.Математика. Текст работы. Применение инверсии при построении графиков дробнорациональной функции
 Скачать 411.1 Kb. Скачать 411.1 Kb.
|
|
Содержание Введение .2 1.Обзор литературы 1.1.Что такое функция? ..3 1.2.Что такое график функции………………………………………………….. 4 1.3. Виды функций и их графики …………...…………………………………...5 1.4. Что же такое инверсия?...................................................................................8 1.5.Условия инвертности точек..............................................................................8 1.6.Свойства инвертных точек…………………………………………………...9 2.Практическая работа 2.1. Инверсия относительно оси OX 10 2.2. Свойства инверсии относительно оси OX 10 2.3. Алгоритм построения графиков с помощью метода инверсии……….....11 2.4. Инверсия относительно оси OY………………...………………..………...11 Заключение……………………………………………………………………….12 Литература……………………………………………………………………….13 Введение. Задачи: Знакомство с методом инверсии. Рассмотрение инверсии относительно прямой, осей координат. Изучение свойств инверсии. Практическое применение инверсии при построении графиков и решении уравнений Сформировать умения и навыки работы с научной литературой, совершенствовать навыки по использованию современных технических средств для сбора и систематизации информации, подготовки текстов и презентаций, выполнения эскизов и макетов. Цель: Изучить метод инверсии и его применение при построении графиков функций. Тема: применение инверсии при построении графиков дробно-рациональной функции. Предмет исследования: графики дробно-рациональных функций. Проблема: Недостаточность теоретического и практического материала по обозначенной теме в действующих школьных учебных пособиях. Гипотеза исследования: использование способа инверсии при построении графиков дробно-рациональных функций упрощает этот процесс. Практическое применение: изучение и систематизация информации о способе инверсии при построении графиков функций поможет в создании плана уроков по данной теме, направленных на повышение навыков учеников в построении нестандартных графиков. Актуальность работы: задания по преобразованию графиков включены в задания по ОГЭ и ЕГЭ, являющиеся обязательными экзаменами. Изучение методов преобразования графиков поможет в выполнение экзаминационных заданий и ускорит выполняемую работу. 1.Обзор литературы. 1.1.Что такое функция? Математика— наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов. Одним из объектов, изучающихся в математике является функция. Что же это такое? В школе термин "функция" употребляется очень часто и особых проблем не доставляет, пока с ним не начинают работать. Это понятие является одним из главнейших во всей математике, науке, технике. Без него – никак. Чтобы дать определение функции начнём с бытового представления о ней. Ключевое слово в данном понятии – зависимость или взаимосвязь. В повседневности мы часто сталкиваемся с функциональными зависимостями. Рассмотри их на примерах из жизни. Человек опаздывает на важную встречу. Что же он будет делать? Наверное, пойдёт быстрее, ведь все точно знают, что чем быстрей идёшь, тем меньше время на дорогу. Это общий закон. Время в пути зависит от скорости передвижения. Или, говоря более научно: время в пути есть функция скорости передвижения. Ещё пример. Человек на дальность бросает камушек в воду. Разумеется, он старается швырнуть его посильнее. И здесь работает постоянный закон: дальность полёта зависит от силы броска. Другими словами: дальность полёта есть функция силы броска. Если какая-то величина А зависит от другой величины В, говорят, что величина А есть функция величины В. Именно в этом и заключается суть функции. В мире существует огромное число зависимостей величин и для записи этих зависимостей используется общая формула: y = f (x)Где y – функция или зависимая переменная. Справа - х, независимая переменная или аргумент. X пишется в скобочках. Буква f - все действия над иксом. Таким образом, функцией называется правило f, по которому каждому элементу х множества Х ставится в соответствие единственный элемент у множества У. 1.2.Что такое график функции? График функции является графическим отображением поведения функции на координатной плоскости или в пространстве. Если выразить эту же мысль математическим языком, то графиком функции является множество точек, абсциссы которых представляют собой возможные значения аргумента х, а ординаты — соответствующие им значения функции у. График функции в математике обозначает представление геометрического образа функции. Также график функции обозначают как геометрическое место точек на плоскости, для которых значения x и значения y связывает указанная функция. Точка с координатами (х, у) может принадлежать графику функции f только в том случае, когда у = f(x). Следовательно, функцию адекватно описывает ее график. Рассмотрим пример графика функци y=2x+5 (рис.1). Такая функция называется линейной. 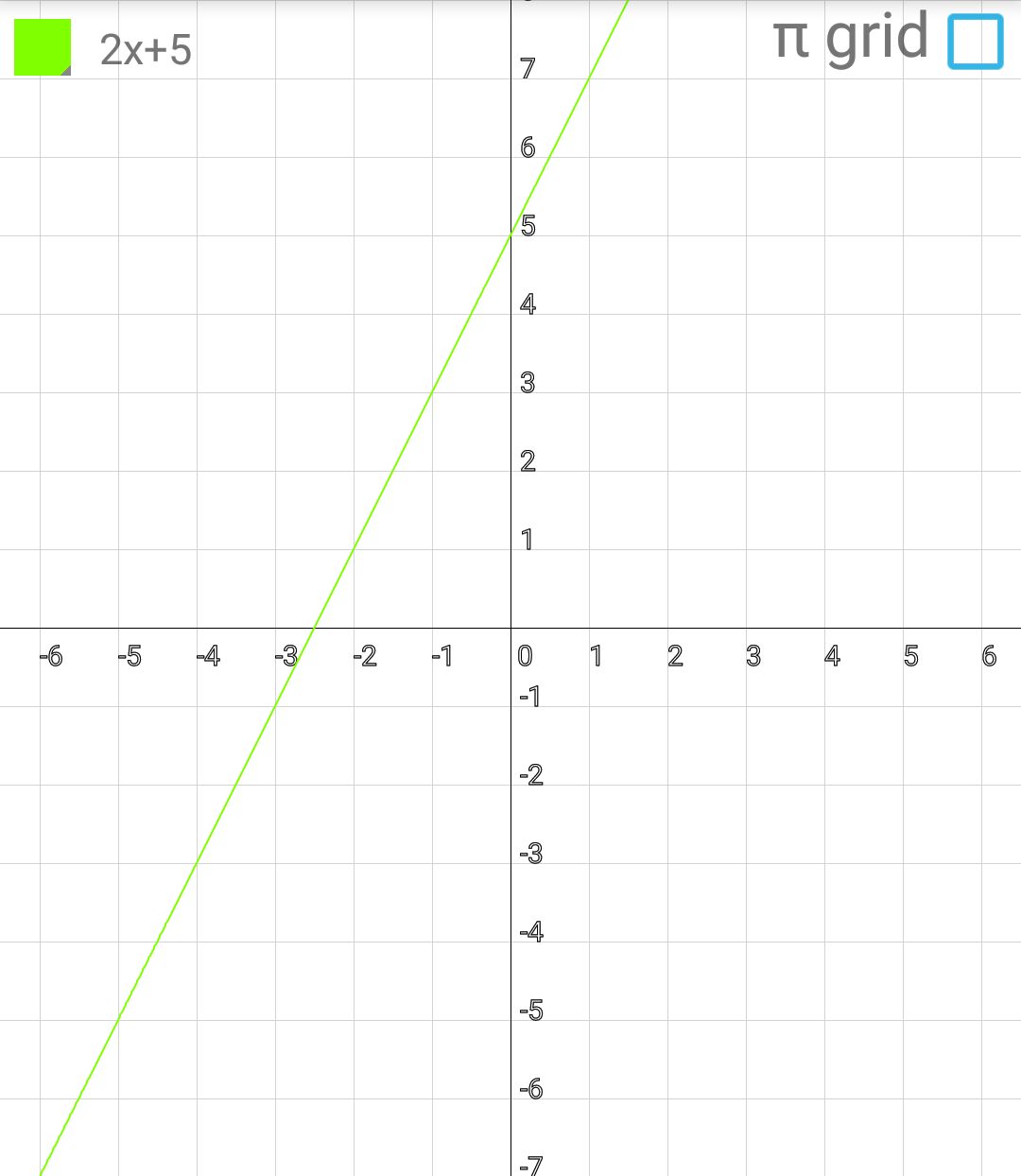 График линейной функции. Рис.1 Проверить правильность построения можно, подставив абсциссу любой из точек графика в функцию, и, получив значение соответствующей ординаты, сравнить ее с реальной. Подставим в уравнение линейной функции вместо переменной х значение 1 и выполним расчет значения у: y=2*1+5 Получили значение у = 7, что соответствует реальным координатам. Таким же образом можно проверить и любые другие координаты точек графика. 1.3.Виды функций и их графики. 1. Линейная функция (y=kx+b) 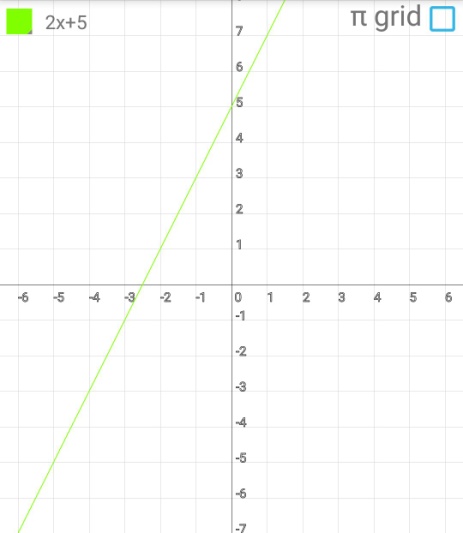 2. Прямая пропорциональность (y=kx)  3. Обратная пропорциональность (y=k/x)  4. Квадратная функция (y=ax2+bx+c) 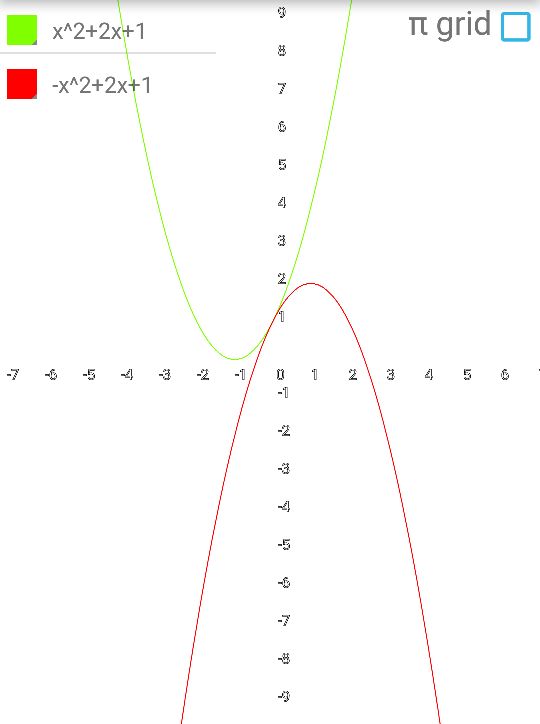 5. Кубическая функция (y=x3) 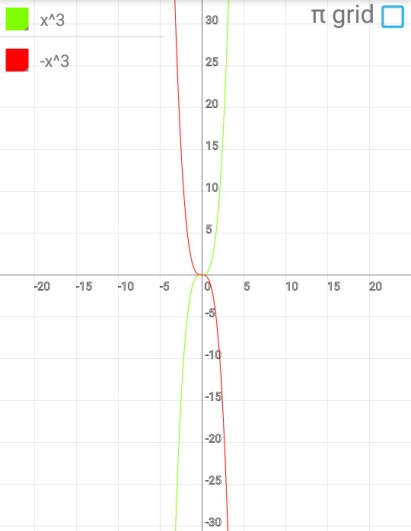 6. Функция модуля (y=|x|) 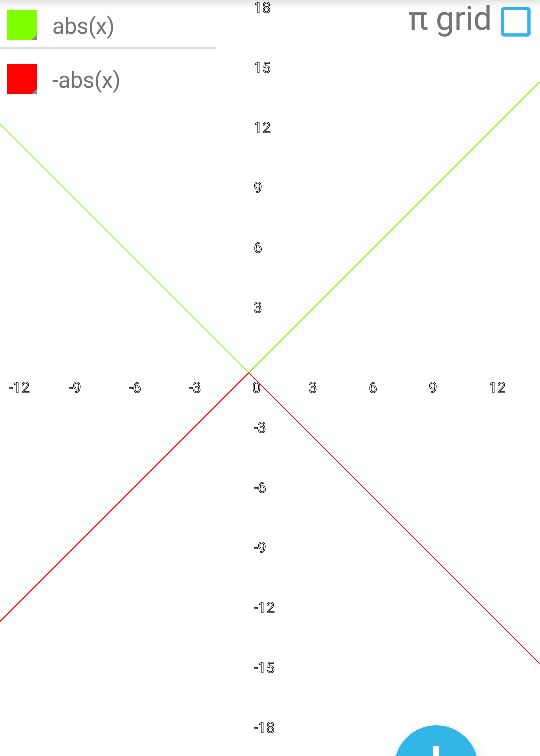 7. Корень из x (y=√x)  8. Синус и косинус (y=sin x, y=cos x) 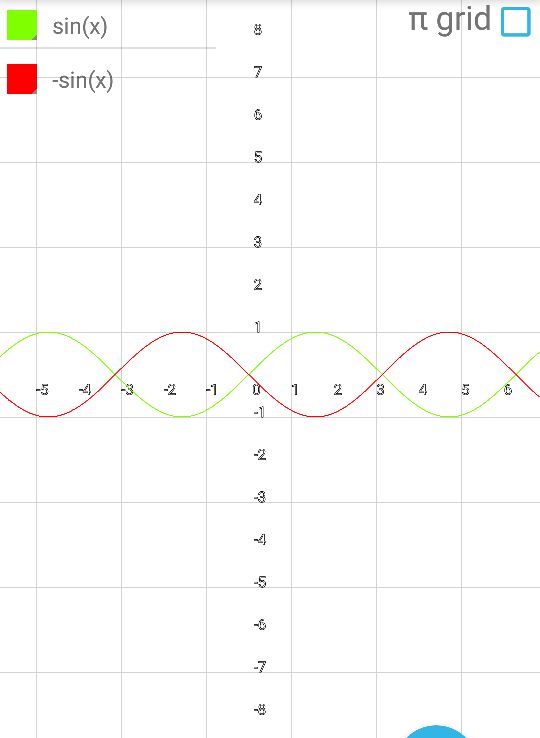 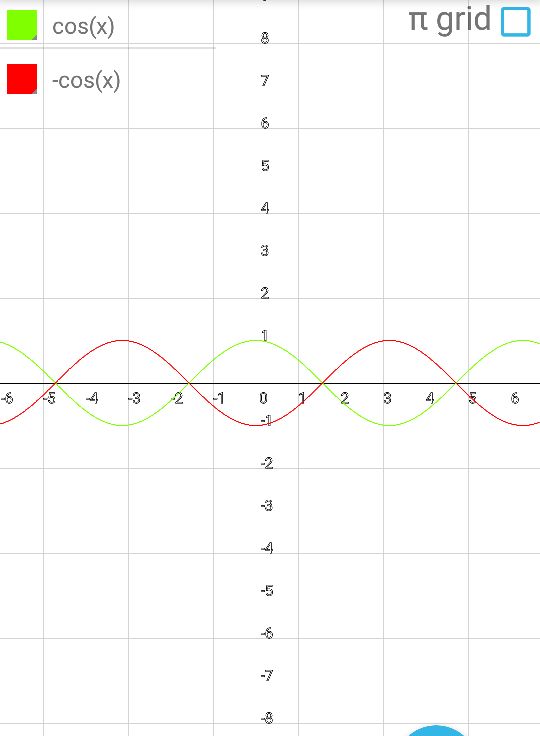 9. Тангенс (y=tg x) 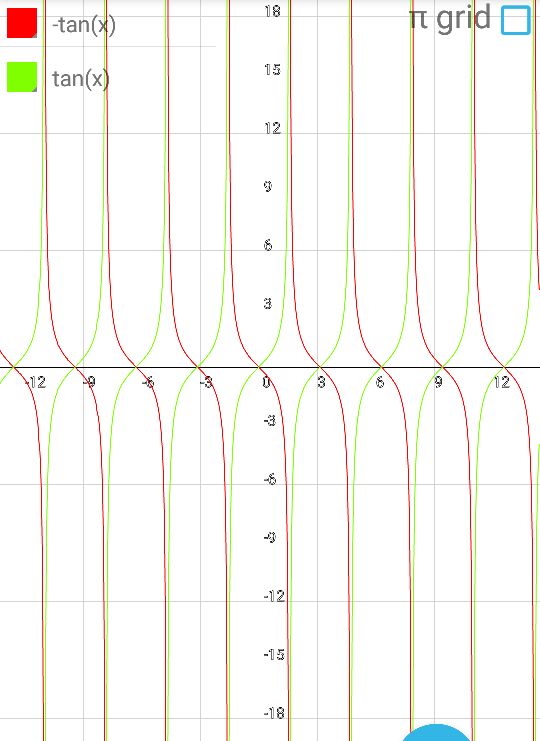 Способ инверсии при построении графиков. 1.4.Что же такое инверсия? Инверсия - изменение нормального положения компонентов, расположение их в обратном порядке. (Толковый словарь С.И. Ожегова). Инверсия (от лат. Inversion – переворачивание, перестановка) – термин, относящийся к перестановкам в математике. 1.5.Условия инвертности точек. Точка В называется инвертной точке А относительно прямой (оси) е, если: 1) эти точки лежат по одну сторону относительно е; 2) отрезок, их соединяющий, перпендикулярен оси е; 3) произведение расстояний от этих точек до е равно 1 (ОА∙ОВ = 1) 4) для точек оси е инвертных нет. 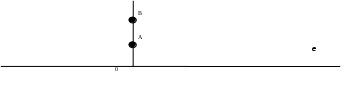 1.6.Свойства инвертных точек. 1. Если точка удалена на расстояние 1 от оси инверсии (при этом неважно в положительном или отрицательном от нее направлении), то инвертная ей –она сама. 2. Инверсия относительно оси Ox: у инвертных точек одинаковые абсциссы, а ординаты – взаимно-обратные числа, поэтому при построении точек-образов происходит движение исходных точек по вертикальным прямым. Инверсия относительно оси Oy: у инвертных точек одинаковые ординаты, а абсциссы – взаимно-обратные числа, поэтому при построении точек-образов происходит движение исходных точек по горизонтальным прямым. 3. Точки далекие от оси инверсии, переходят в точки близкие к оси и наоборот, близкие к оси переходят в далекие. 4. Если точка лежит на оси инверсии, то инвертной для нее не существует, а через нее проходит асимптота графика-образа, причем асимптота вертикальная, если она получена при инверсии относительно оси Oy и горизонтальная, если при инверсии относительно оси Ox. 2.Практическая работа 2.1.Инверсия относительно оси OX. 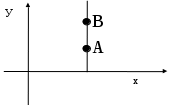 График функции g(x) =1/f(x) получается из графика функции y=f(x) инверсией относительно оси ОХ. Т.е. значения ординат точек функции g(x) =1/f(x) заменяется на значение, обратное абцессе функции. Буквенная запись: (x;y)→(x;1/y) 2.2.Свойства инверсии относительно оси OX. Построив график функции с помощью инверсии относительно оси OX можно сделать вывод о его свойствах: 1. Если f(x)>0, то >0. Если f(x) <0, то <0. 2. Если y=f(x) имеет корни х= х1…., т.е. f(x)=0, то g(x)=1/ f(x) имеет вертикальные асимптоты х=х1 …. 3.Если у графика функции y=f(x) есть горизонтальная асимптота у=0,то 1/ f(x) имеет асимптоту у=0. Если у графика функции y=f(x) есть горизонтальная асимптота y=b при x→∞, то график функции g(x)=1/f(x) будет иметь горизонтальную асимптоту y=1/b. 4.Если f(-x)= f(x), то g(-x)= 1/f(-x)=1/f(x)= g(x) Если f(-x)= -f(x), то g(-x)=1/f(-x)=1/f(x)= -g(x). 5.Если f(x) – периодическая функция, то 1/f(x)- периодическая функция. 6. Если f(x) сохраняет знак на множестве X и возрастает на нем, то 1/f(x) убывает на этом множестве. Если f(x) сохраняет знак на множестве X и убывает на нем, то 1/f(x)возрастает на этом множестве. 7.Наибольшее значение функции изменяется и становится наименьшим, и наоборот. Максимум становится минимумом, и наоборот. 8. Если при x → ∞ f(x) → 0, то в графике инверсии 1/f(x) → ∞. Если при x → ∞ f(x) → ∞, то в графике инверсии 1/f(x) → 0. 2.3.Алгоритм построения графиков с помощью метода инверсии. 1.Строим график функции y=f(x). 2.Через точки пересечения графика функции y=f(x) с осью ОХ проводим вертикальные асимптоты или вынуть из области определения нули функции. 3.Строим вспомогательные прямые у=1, у=-1. 4.Промежутки знакопостоянства сохраняем. 5.Сохраняем четность функции (симметрия графика) 6.Сохраняем периодичность функции. 7.Меняем промежутки возрастания (убывания) на промежутки убывания (возрастания). 2.4.Инверсия относительно оси ОY. 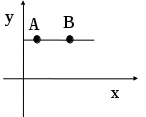 График функции g(x)=f(1/x) получается из графика функции y=f(x) инверсией относительно оси ОY. Т.е. значения абсцисс точек функции g(x) =1/f(x) заменяется на значение, обратное абцессе функции. Буквенная запись: (x; y)→(1/x; y). Заключение. В ходе выполнения работы нами был изучен метод инверсии и его применение при построении графиков дробно-рациональных функций. Гипотеза была доказана. Список литературы. А.П. Карп «Даю уроки математики»: Кн. для учителя: Из опыта работы. - М.: Просвещение, 1992.-191 с. Н.Я. Виленкин «Алгебра 9» (учебное пособие для учащихся школ и классов с углубленным изучением математики). (М., «Просвещение», 1996) И.М. Гельфанд, Е.Г. Глаголева, Э.Э. Шноль Функции и графики (основные приемы). – М.: Издательство «Наука», 1973.-96 с. http://helpmatan.ru/ http://ru.wikipedia.org/wiki/Инверсия http://www.myshared.ru/slide/1075197/ http://dropdoc.ru/doc/1196633/postroenie-grafikov-funkcij-e-lementarnymi https://nsportal.ru/ap/library/drugoe/2018/04/10/soobshchenie-po-teme-primenenie-inversii-dlya-postroenie-grafikov  |
