урок 91. Применение производной для отыскания наибольших и наименьших значений величин
 Скачать 165.73 Kb. Скачать 165.73 Kb.
|
|
Название предмета: Алгебра и начала анализа Класс:10 УМК: Алгебра и начала математического анализа (базовый и углубленный уровни). Мордкович А.Г., Семенов П.В. 10 класс – ИОЦ «Мнемозина», 2011 г. Тема урока: Применение производной для отыскания наибольших и наименьших значений величин» Общее количество часов, отведенное на изучение темы: 3часа 2 урок в системе уроков по теме. Тарасова Н.Н. Тема: « Применение производной для отыскания наибольших и наименьших значений величин» Цели: Образовательная: -совершенствовать навыки и умения учащихся применения производной функции для нахождения наибольшего и наименьшего значений непрерывной функции на заданном промежутке, продолжить работу по подготовке к ЕГЭ. Развивающая: - развивать у учащихся навыки самостоятельного выполнения заданий и решения примеров, а также навыки взаимооценивания работы учащихся класса и осмысления собственного участия в процессе учебной деятельности на уроке; Воспитательная: -воспитывать у учащихся умение выслушать и принимать во внимание взгляды других людей, умение справляться со сложностью. Ход урока. 1.Организационный момент. Девиз урока: «Решай, ищи, твори и мысли». 2.Актуализация опорных знаний . Учащиеся поднимают руку, если согласны с утверждением, и не поднимают – если не согласны. В точке возрастания функции её производная больше нуля. (Верно). Если производная функции в некоторой точке равна нулю, то в этой точке имеется экстремум! (Неверно). Производная произведения равна произведению производных. (Неверно). Наибольшее и наименьшее значения функции на некотором отрезке наблюдаются или в стационарных точках, или на концах отрезка. (Верно). Любая точка экстремума является критической точкой. (Верно). Работа с раздаточным материалом ( у каждого уч-ся на столе лежит лист с заданиями из банка ЕГЭ) 1 задание: Функция y = f(x) определена на промежутке (- 6; 6). На рисунке изображён график её производной. Найдите точки, в которых производная функции равна нулю. 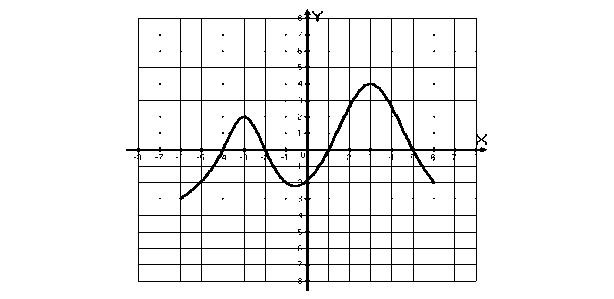 2 задание: Функция y = f(x) определена на промежутке (-6; 5). На рисунке изображён график её производной. Укажите количество промежутков, на которых функция возрастает. 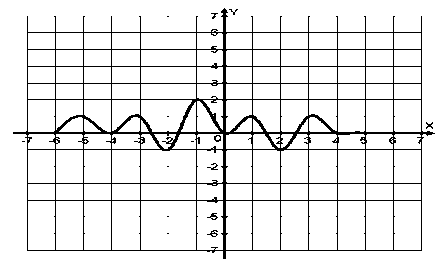 3 задание: Функция y = f(x) определена на промежутке (-4; 5). На рисунке изображён график её производной. Найдите точку минимума функции y = f(x).  4 задание: Функция y = f(x) определена на промежутке (-4; 5). На рисунке изображён график её производной. Найдите точку максимума функции y = f(x). 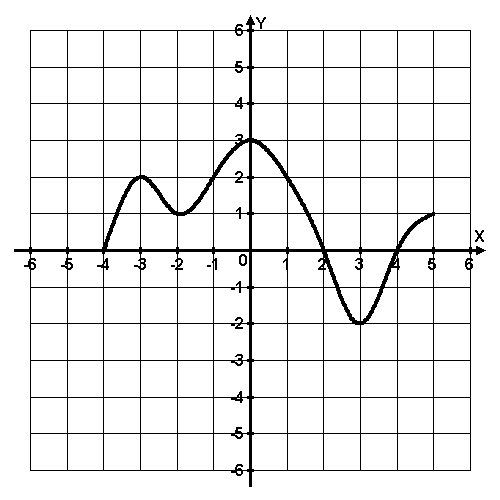 5 задание: Функция y = f(x) определена на промежутке (-5; 5). На рисунке изображён график её производной. Укажите точку, в которой функция принимает наименьшее значение. 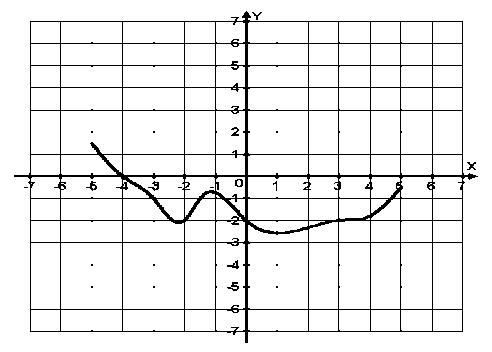 Ответы: 1 задание: х = - 4; х = - 2; х = 1; х = 5 2 задание: 5 3 задание: х = 3 4 задание: х = 2 5 задание: х = - 4 На ЕГЭ по математике часто встречаются задания на нахождение наибольшего и наименьшего значений функции на отрезке . Вспомним алгоритм нахождения наибольшего и наименьшего значений непрерывной функции на заданном промежутке,  Алгоритм нахождения наибольшего и наименьшего значения функции на промежутке: 1. Найти область определения функции и определить, принадлежит ли заданный отрезок области определения. 2. Найти производную заданной функции f`(x). 3. Найти стационарные точки: f`(x) = 0; 4. Выяснить, какие из стационарных точек принадлежат данному отрезку [a; b]. 5. Найти значения функции в тех стационарных точках, которые входят в отрезок, а также f (a) и f (b). 6. Выбрать из полученных значений функции наибольшее и наименьшее: У наиб = У наим.= [a; b] [a; b] Постановка проблемной ситуации и её решение. При решении многих задач часто приходится находить наибольшее или наименьшее значение функции не на отрезке, а на интервале. Например, найти наибольшее значение функции f (х) = 60х - 1,5х2 на интервале (0; 40). - Можно ли для решения этой задачи использовать данный алгоритм? ( Учащиеся выдвигают гипотезу, что можно использовать правило нахождения наибольшего и наименьшего значений функции на отрезке, а затем значения функции на концах отрезка отбросить.) Чтобы проверить выдвинутую вами гипотезу, решим предложенное задание. Сначала найдем наибольшее значение функции на отрезке [0;40]. Используем изученное правило: 1. Найдем производную функции f (х) = (60х - 1,5х )' =60 - Зх. 2. Найдём критические точки функции: 60 - Зх = 0, Зх = 60, х = 20. 3. Проверим, принадлежит ли критическая точка данному отрезку: 20  [0;40] [0;40]4. Вычислим значение функции в критической точке и на концах отрезка: f(20) = 60*20 - 1,5*202 - 1200 - 600 = 600, f(0) = 0. f(40) =60 * 40 - 1,5 * 402= 2400 - 2400 = 0. Наибольшее значение функция достигает внутри отрезка [0;40], значит и внутри интервала (0; 40). max f(x) = У наиб = f(20) = 600. Формирование умений и навыков. Задания урока разделяются на две группы. 1 группа отработка умений и навыков применения алгоритма, 2 группа задач – работа в парах на развитие навыка самостоятельного выполнения заданий, а также на формирование умений самооценки и взаимооценки. 1 группа заданий № 32.10(а) , 32.12(а); 32.13(а) (работа учащихся на местах с последующей проверкой у доски) № 32.10 (а) Дано: Найдем производную Найдем критические точки Из них выбираем те, которые принадлежат данному отрезку: Вычислим: Ответ: № 32.12(а) Решение: 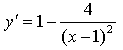 2) 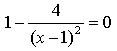  х – 1 = 2 или х – 1 = –2 х = 3 х = –1 3) а) [2; 4]. Данному отрезку принадлежит точка х = 3. 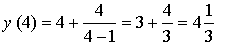 О 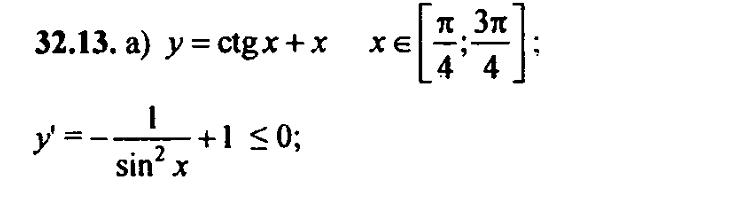 твет: твет: 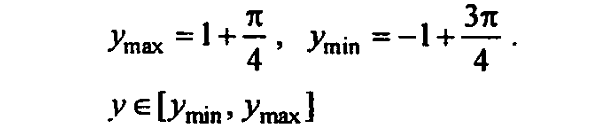 2. группа задач. Решение задач открытого банка ЕГЭ. ( работа в парах). ( Самопроверка и взаимопроверка. За каждый правильно решенный пример «+» - 1 балл. Поставьте оценки. Если получили 3 б – «5», если одна ошибка– «4», если 2 ошибки – «3») Тест В В 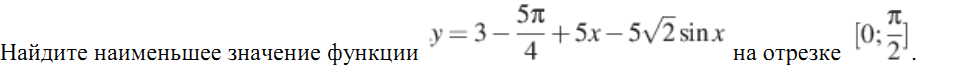 3. 3.Ответы: 1В.: -54; -1; 1. 2В: 6; 5; -2 5.Подведение итогов урока. Обсуждение с учащимися достижения цели и задач урока. Аргументированное комментирование оценок за урок. 6. Домашнее задание: п.32стр. 192- 197 № 32.13 (в), № 32.15(а, в) , заданиями В12 ЕГЭ- найти и решить – 2-3 задания.. |
