|
|
урок 90. Применение производной для отыскания наибольших и наименьших значений величин
Название предмета: Алгебра и начала анализа
Класс:10
УМК: Алгебра и начала математического анализа (базовый и углубленный уровни). Мордкович А.Г., Семенов П.В. 10 класс – ИОЦ «Мнемозина», 2011 г.
Тема урока: «Применение производной для отыскания наибольших и наименьших значений величин»
Общее количество часов, отведенное на изучение темы: 3часа
1 урок в системе уроков по теме
Тарасова Н.Н
Тема урока: «Применение производной для отыскания наибольших и наименьших значений величин»
Цели урока:
Образовательная научить находить наибольшее и наименьшее значения непрерывной функции на промежутке, сформулировать основные теоретические положения, рассмотреть алгоритм решения такого вида задач, отработать шаги алгоритма, рассмотреть частные случаи;
Развивающая развивать умение работать в команде( паре), умение читать график функции, анализировать, сравнивать, обобщать и делать выводы, развивать исследовательские умения.
Воспитательная воспитывать упорство, трудолюбие, открытую познавательную позицию.
учащиеся должны знать:
- алгоритм отыскания наибольшего и наименьшего значения непрерывной функции на промежутке;
учащиеся должны уметь:
- находить наибольшее и наименьшее значение непрерывной функции на промежутке по алгоритму, изученному на уроке;
- применять алгоритм для нахождения наибольшего и наименьшего значения непрерывной функции на промежутке для решения задач.
ХОД УРОКА
1. Организационный момент.
Включает в себя приветствие учителем класса, проверку готовности кабинета к проведению урока, проверку отсутствующих.
2. Актуализация знаний. Устная работа.
1. Найдите производную функции:
а) у = sin х , б) у = tg х , в) у = х4 - 2х2 + 3, г) у = х4, д) у = cos 2х,
2. Найдите критические точки функции: f(x) = 2х - х2.
3. Вычислите f(2), если f(x) = 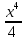 - Зх + 5 . - Зх + 5 .
4. Вычислите значение производной функции у =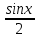 в точке х0 = в точке х0 =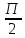 . .
Учитель: 1) Используя график функции, найдите интервалы монотонности и точки экстремума, а также наибольшее и наименьшее значения функции.
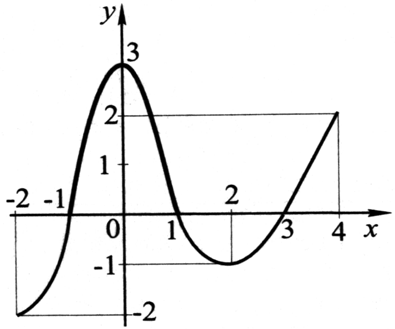
Учитель: Прежде чем приступить к изучению нового материала, прошу вас обратить внимание, что наибольшее или наименьшее значение функции не всегда совпадает с максимум или минимум.
Из курса 7-го класса вы умеете строить графики функций и находить по ним минимальные и максимальные значения. Однако, построение графика данной функции заняло бы очень много времени. Скажите, пожалуйста, а можем ли мы найти наибольшее и наименьшее значения функции каким - нибудь другим способом?
Сегодня мы будем искать более простые пути решения данной задачи.
Эпиграф к уроку: Единственный путь, ведущий к знанию, - деятельность.
Бернард Шоу
3. Изучение нового материала.
Учитель: Большая группа задач в технике, в естествознание, в экономике, в повседневной деятельности людей связана с необходимостью определения условий, при которых некоторая величина принимает наибольшее или наименьшее значения.
Например:
1) Где нужно расположить мост через реку, чтобы путь из А в В, находящихся на разных берегах, был наименьшим?
2) Требуется огородить участок с заданным периметром, чтобы площадь его была наибольшей (если перевести эту задачу на язык математики: какой из всех прямоугольников заданного периметра имеет наибольшую площадь?)
Как видите, решение задач на нахождение наиболее выгодных условий занимали умы людей с древних времен. Но только с появлением дифференциального исчисления был найден метод, позволяющий решать эти задачи по единой схеме.
Д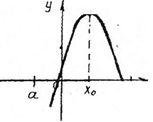 алее предложить учащимся сформулировать тему урока и определить его цели, после ответов учащихся записать тему урока. алее предложить учащимся сформулировать тему урока и определить его цели, после ответов учащихся записать тему урока.
Рассмотрим функцию у = f(x) на отрезке [а;Ь].
Что можно сказать об этих функциях? (Ответ:
все функции непрерывны на отрезке [а;Ь]). Как называется точка х0 на рис. 1 ? (Ответ: точка максимума)
Ч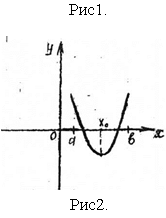 то можно сказать о значении функции в этой точке? то можно сказать о значении функции в этой точке?
(Ответ: в этой точке функция принимает наибольшее значение). Аналогично рассмотрим рис.2.
Охарактеризуйте функцию, изображенную на рис 3.
(Ответ: функция непрерывна на отрезке [а;Ь], х1- точка минимума, х2 - точка максимума).
М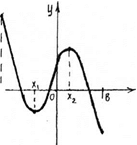 ожно ли утверждать, что в точке минимума функция имеет наименьшее значение, а в точке максимума - наибольшее значение? (учащиеся дают ожно ли утверждать, что в точке минимума функция имеет наименьшее значение, а в точке максимума - наибольшее значение? (учащиеся дают tлибо правильный ответ, либо затрудняются). Для того, чтобы дать правильный ответ, сравните значения функции в точке минимума и на конце отрезка в точке в.(Ответ: значение функции на конце отрезка меньше, чем в точке минимума). Рис3
Аналогично сравните значение функции в точке максимума со значением функции на конце отрезка в точке а. (Ответ: значение функции на конце отрезка больше, чем в точке максимума).
Какой можно сделать вывод? (Ответ: непрерывная функция может достигать наибольшего и наименьшего значений как внутри отрезка, так и на его концах.)
После данных рассуждений приходим к важным выводам.
Вывод 1. Если функция непрерывна на отрезке, то она достигает на нём и своего наибольшего, и своего наименьшего значений.
3) В каких из рассмотренных случаев функция достигает своего наибольшего и наименьшего значений на концах отрезка?
4) В каких случаях функция достигает своего наибольшего и наименьшего значений внутри отрезка?
Вывод 2. Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.
5) В случае 1 чем являлись для функции точка, в которых она достигла наибольшего значения на заданном отрезке?
6) В каких ещё случаях функция достигла своего наибольшего или наименьшего значения в точках экстремума?
Вывод 3. Если наибольшее или наименьшее значение функции достигается внутри отрезка, то только в точке экстремума.
7) Может ли функция достигать своего наибольшего и наименьшего значений и не на концах отрезка, и не в точках экстремума?
Вывод 4. Своего наибольшего и наименьшего значений функция может достигать или на концах отрезка, или в точках экстремума, принадлежащих этому отрезку.
Из всех полученных выводов вытекает алгоритм нахождения наибольшего и наименьшего значений непрерывной функции на отрезке, который учащиеся записывают в тетрадь.
Учитель: Это алгоритм нахождения наибольшего и наименьшего значений функции
y=f (x) на отрезке [a; b]. Запишите его себе в тетрадь.
Учащиеся записывают с доски алгоритм в тетрадь
Запись в тетрадях:
Алгоритм нахождения наибольшего и наименьшего значений функции
y=f (x) на отрезке [a; b]:
для того, чтобы найти наибольшее и наименьшее значения функции
y=f (x) на отрезке [a; b] нужно:
1. Найти область определения функции и определить, принадлежит ли заданный отрезок области определения.
2. Найти производную заданной функции f`(x).
3. Найти стационарные точки: f`(x) = 0;
4. Выяснить, какие из стационарных точек принадлежат данному отрезку [a; b].
5. Найти значения функции в тех стационарных точках, которые входят в отрезок, а также f (a) и f (b).
6. Выбрать из полученных значений функции наибольшее и наименьшее:
У наиб = У наим.=
[a; b] [a; b]
|
Учитель: А теперь рассмотрим пример применения данного алгоритма: найдем наибольшее и наименьшее значения функции f (x) = 2x3-9x2 на [1;4].
Учащиеся вместе с учителем у доски разбирают пример применения алгоритма, отвечают на наводящие вопросы и делают записи в тетради
Запись на доске и в тетрадях:
Найти наибольшее и наименьшее значения функции f (x) = 2x3-9x2 на отрезке [1;4].
1) функция определена и дифференцируема на R;
2) f `(x) = 6x2-18х = 6x(x-3);
3) стационарные точки: f `(x) = 0; х = 0 или х = 3;
4)
0  [1;4], [1;4],
3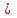 [1;4]. [1;4].
5) f (3) = 54-81 = -27;
f (1) = 2-9 = -7;
f (4) = 128-144 = -16.
6) Унаиб. = f (1) = -7; Унаим. = f (3) = -27;
[1;4] [1;4]
|
IV. Первичное закрепление
В первой группе заданий даны элементарные функции, наибольшие и наименьшие значения которых учащиеся смогут найти и без использования производной. А во вторую группу входят задания, при выполнении которых обязательно использование производной.
1-я группа. (Учащиеся выходят по очереди к доске, решают примеры, комментируют решение, остальные – решают на месте, делая записи в тетради.)
1. № 32.1 (а; г)
Решение:
а) у = 3х – 6, [–1; 4]
Рассуждения могут быть следующими:
– функция у = 3х – 6 является линейной;
– она монотонно возрастает на всей числовой прямой;
– своего наибольшего и наименьшего значений данная функция будет достигать на концах отрезка [–1; 4];
– поскольку функция возрастающая, то при х = –1 её значение будет наименьшим, а при х = 4 – наибольшим.
у (–1)= 3 · (–1) – 6 = –9
у (4) = 3 · 4 – 6 = 6
Ответ: унаим = –9; унаиб = 6.
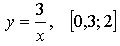
г)
данная функция монотонно убывает на своей области определения.
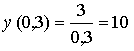 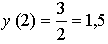
Ответ: унаим = 1,5; унаиб = 10.
2. № 32.2 (б),
При выполнении данных заданий можно использовать два способа решения: воспользоваться знаниями о свойствах функций и используя производную. В этом случае работу можно организовать по группам
Решение:
№ 32.2 (б).
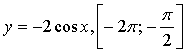
1-й способ.
Замечаем, что на указанном промежутке функция у = cos х принимает все свои значения, то есть [–1; 1]. Значит, наибольшим значением функции 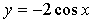 будет 2, а наименьшим –2. будет 2, а наименьшим –2.
2-й способ.
Воспользуемся алгоритмом нахождения наибольшего и наименьшего значений функции на отрезке.
1) 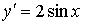
2) 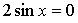 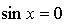 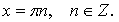
На отрезке 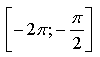 получим два корня получим два корня 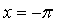 и и 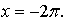
3) 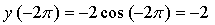

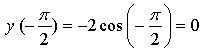
Ответ: 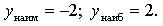
3. № 32.4 (в), № 32.5 (а; б).
При выполнении этих заданий также можно не использовать производную.
2-я группа.
1. № 32.6 (а).
Решение:
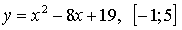
Здесь также можно использовать два способа.
1-й способ.
Графиком данной функции является парабола, ветви которой направлены вверх. Своего наименьшего значения такая функция достигает в точке, которая служит вершиной этой параболы. Найдем её:
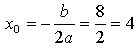
Эта точка входит в рассматриваемый промежуток, причём х = 4 является осью симметрии параболы. Значит, наибольшего значения функция достигает в точке х = –1.
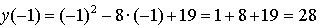
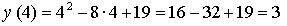
Ответ: 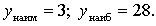
2-й способ.
Воспользуемся алгоритмом нахождения наибольшего и наименьшего значений функции на отрезке.
2. № 32.8 (а)
Функцию, предложенную для рассмотрения в этом упражнении, можно исследовать на наибольшее и наименьшее значения только с помощью производной.
V. Итоги урока.
Вопросы учащимся:
– Всегда ли непрерывная функция достигает наибольшего и наименьшего значений на отрезке?
– Если функция монотонно возрастает на отрезке, то в какой точке она достигает наибольшего значения?
– В каких точках функция может достигать наибольшего и наименьшего значений на отрезке?
– Опишите алгоритм нахождения наибольшего и наименьшего значений непрерывной функции на отрезке.
Домашнее задание: № 32.2 (в), № 32.11. |
|
|
 Скачать 112.28 Kb.
Скачать 112.28 Kb. [1;4],
[1;4],  [1;4].
[1;4].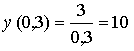
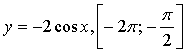
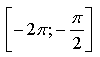 получим два корня
получим два корня 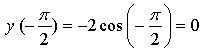

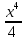 - Зх + 5 .
- Зх + 5 .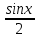 в точке х0 =
в точке х0 =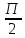 .
.
 алее предложить учащимся сформулировать тему урока и определить его цели, после ответов учащихся записать тему урока.
алее предложить учащимся сформулировать тему урока и определить его цели, после ответов учащихся записать тему урока. то можно сказать о значении функции в этой точке?
то можно сказать о значении функции в этой точке? ожно ли утверждать, что в точке минимума функция имеет наименьшее значение, а в точке максимума - наибольшее значение? (учащиеся дают
ожно ли утверждать, что в точке минимума функция имеет наименьшее значение, а в точке максимума - наибольшее значение? (учащиеся дают