Контрольная. Пример применения ДА Краскела-Уоллиса. Пример. Новые методики тренировки лыжников

Название	Пример. Новые методики тренировки лыжников
Анкор	Контрольная
Дата	25.12.2022
Размер	2.61 Mb.
Формат файла
Имя файла	Пример применения ДА Краскела-Уоллиса.docx
Тип	Документы #862739

Пример применения Н-критерия Краскела-Уоллиса для сравнения нескольких независимых групп.

Пример. Новые методики тренировки лыжников. Исследования, проводимые на протяжении ряда лет, после того, как в практике лыжного спорта стали применяться две новые методики тренировки – методика Иванова и Петрова, дают основания предполагать, что эти методики обеспечивают на дистанции 15 км у мужчин выигрыш по сравнению с традиционной методикой тренировки.

В таблице 1 приводятся отсортированные данные, полученные на соревнованиях на дистанции 15 км для трех групп лыжников: первую группу Х1 тренировали традиционной методикой, вторую группу Х2 тренировали по методике Иванова, третью группу Х3 тренировали по методике Петрова.

Позволяют ли результаты соревнований утверждать, что использование методик Иванова и Петрова позволяет улучшить средний результат в группах спортсменов Х2 и Х3?

Таблица 1– Результаты лыжников на дистанции 15 км (в мин)

Х1	37,47	37,55	37,58	37,62	37,63	38,10	38,70	39,79	51,31	54,13
Х2	37,67	37,75	35,78	37,82	35,83	37,30	36,90	37,99	50,51	54,33
Х3	34,77	35,85	36,88	34,92	34,93	35,40	37,00	37,09	49,61	51,43

Алгоритм решения:

Запускаем пакет STATISTICA 10.
Скопировать из word файла таблицу данных в Excel. Выполнить операцию транспонирования, предварительно выделив интервал А5:С15, ввести формулу =ТРАНСП(А1:К3) и нажать одновременно (Ctrl + Shift + Enter)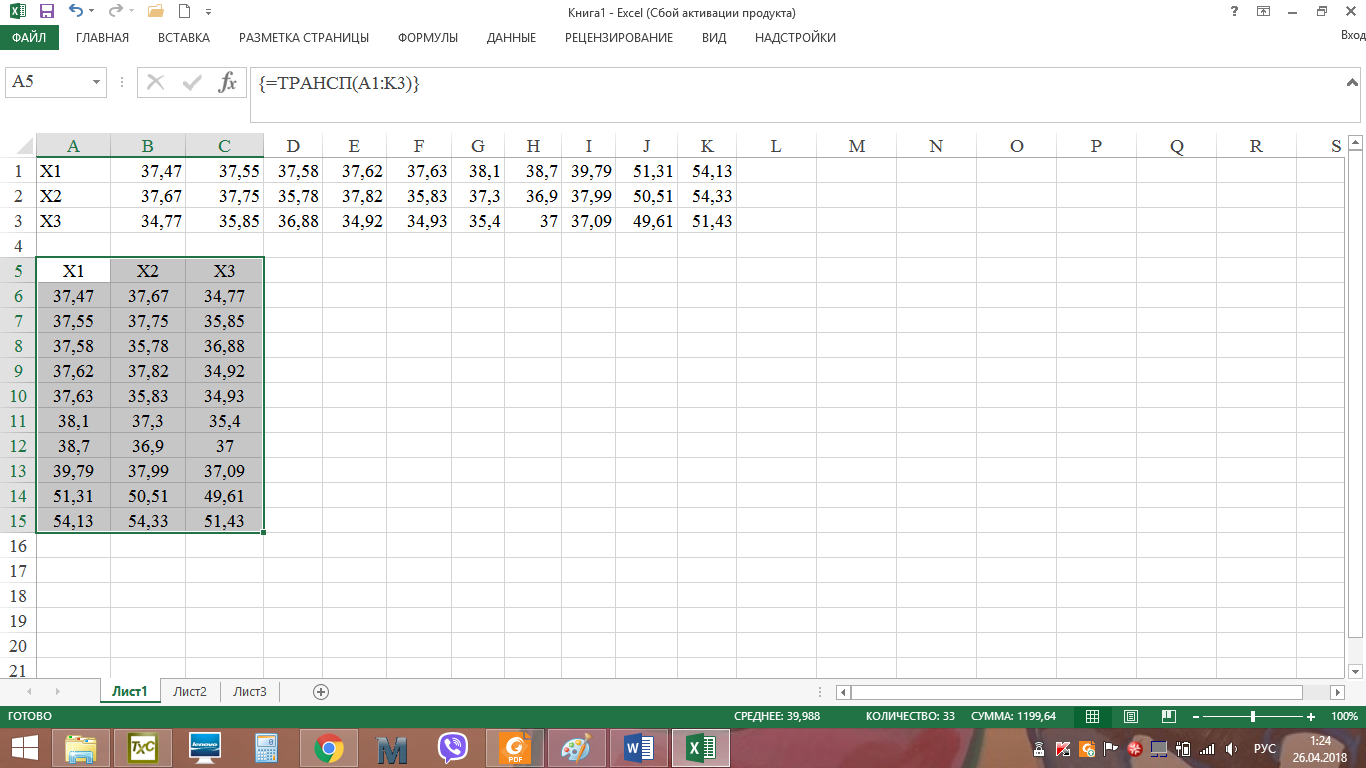

После импортировать данные в STATISTICA.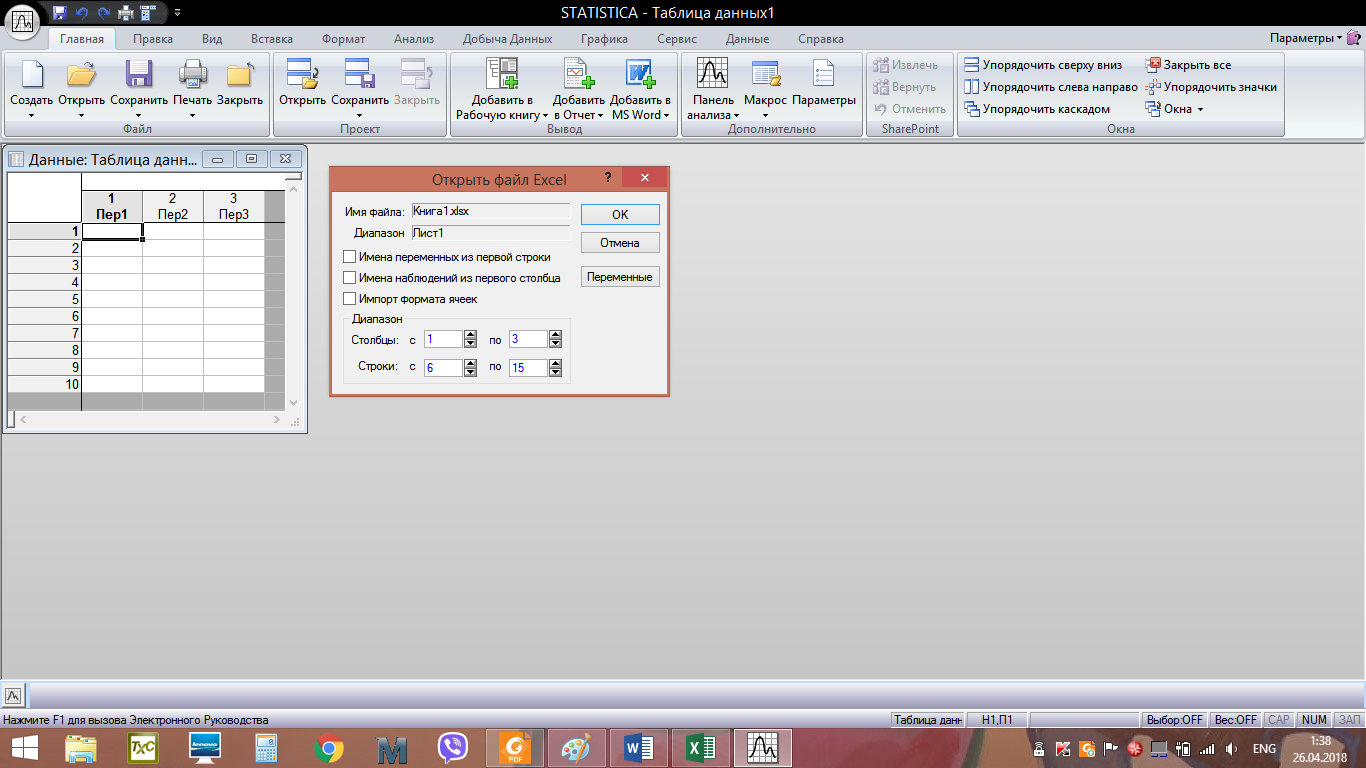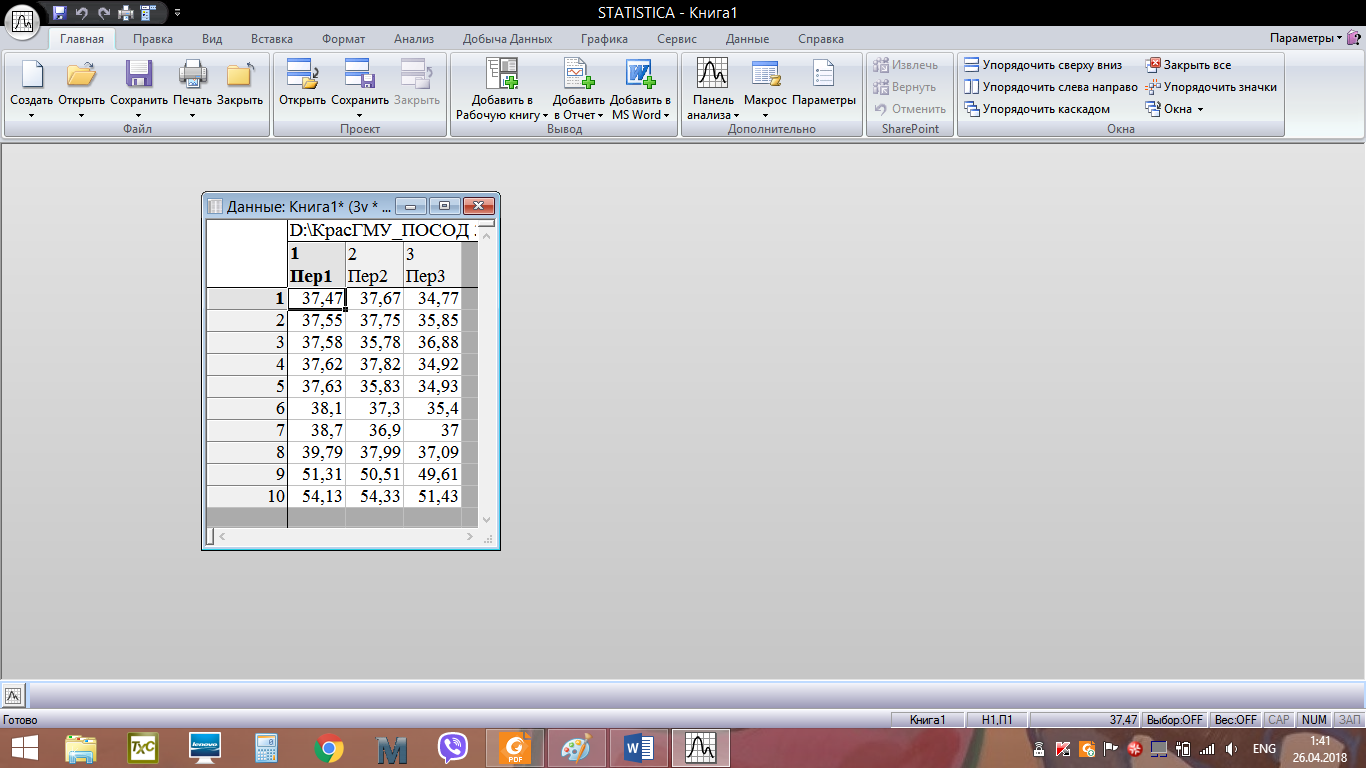

4. Обозначим переменные в столбцах. Вместо Пер1 в строке Имя введем Х1. Затем щёлкнем по правой кнопке перехода >> и введем имя второго столбца Х2. Затем, проделав аналогичное действие, введем имя третьего столбца Х3. Нажмем ОК.

5. Cохраним таблицу под именем Сравнение методик тренировок лыжников.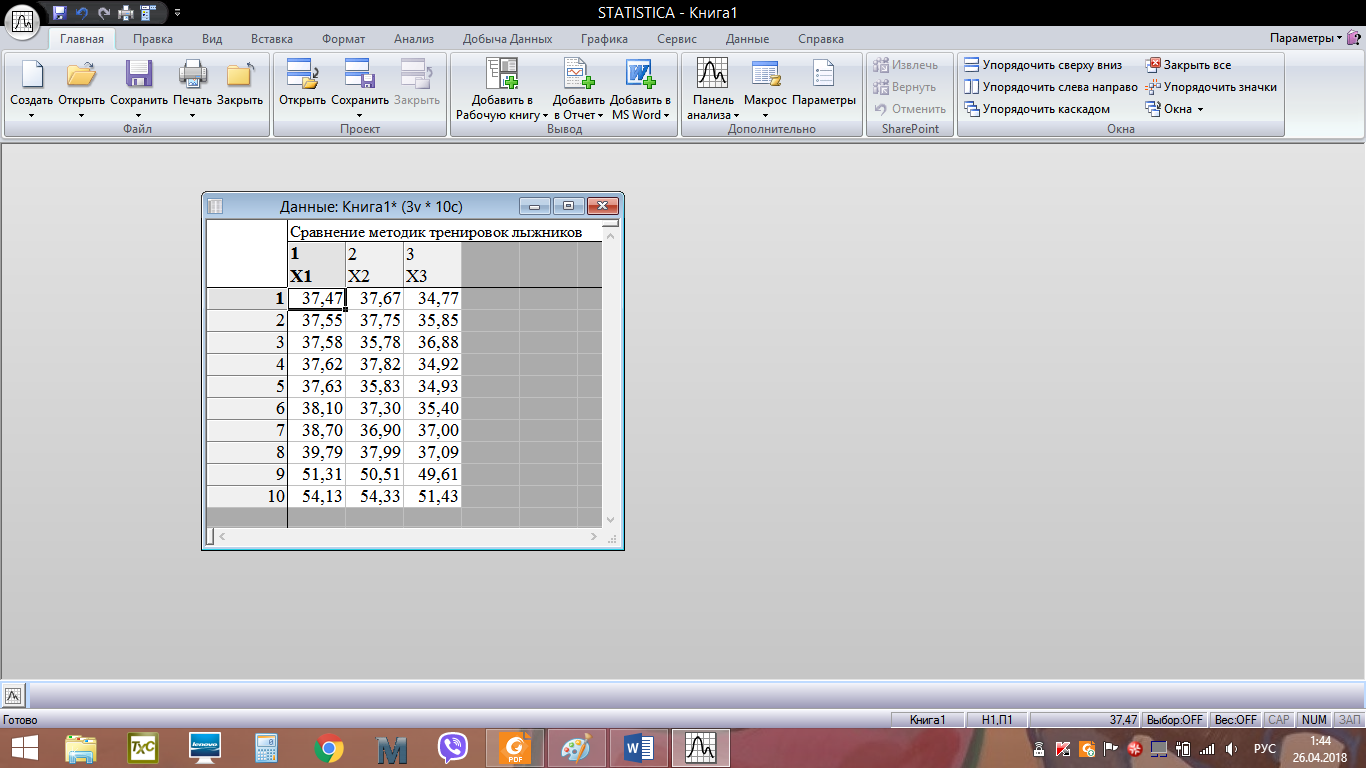

6. Для проверки характера распределения признаков во вкладке Анализ выберем Основные статистики и таблицы. Затем в возникшем окне Основные статистики и таблицы необходимо выбрать пункт Описательные статистики и нажать ОК.

7. В открывшемся окне Описательные статистики нажимаем на кнопку Переменные и мышью выделяем переменные Х1, Х2, Х3. Нажимаем ОК.

8. В окне Описательные статистики выберем вкладку Нормальность и затем выберем опцию Критерий Шапиро-Уилка. Нажмем кнопку Гистограммы. Появятся три гистограммы. Первая из них – для группы Х1, вторая – для группы Х2, третья – для группы Х3. Видно, что во всех группах расчетные значения W-критерия меньше табличного значения 0,842 и вероятность нулевой гипотезы (того, что наблюдаемое распределение соответствует нормальному закону) значительно меньше критического уровня значимости 0,05 (5%). Таким образом, нулевая гипотеза о нормальности распределения здесь отвергается для всех трех групп. Кроме того, очевидно, что гистограммы сильно асимметричны – пики смещены влево.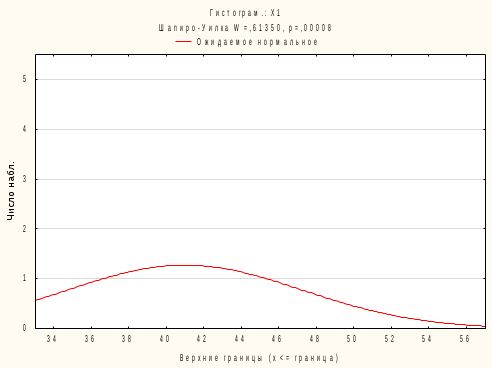

Рис. – Гистограмма распределения результатов лыжников в группе Х1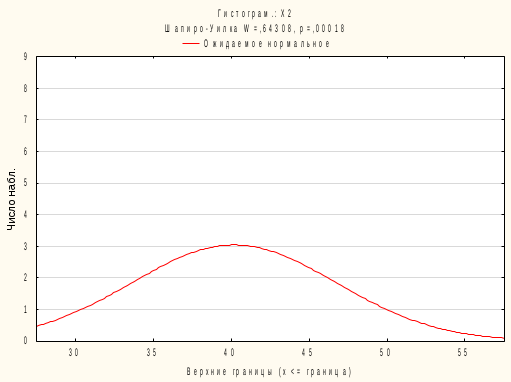

Рис. – Гистограмма распределения результатов лыжников в группе Х2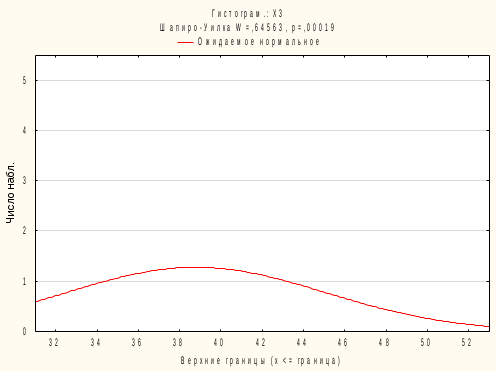

Рис. – Гистограмма распределения результатов лыжников в группе Х3

9. На вкладке Анализ –> Основные статистики и таблицы –> Описательная статистика -> OK. Выберем переменные Х1, Х2, Х3, во вкладке Дополнительно выберем статистические показатели как на рисунке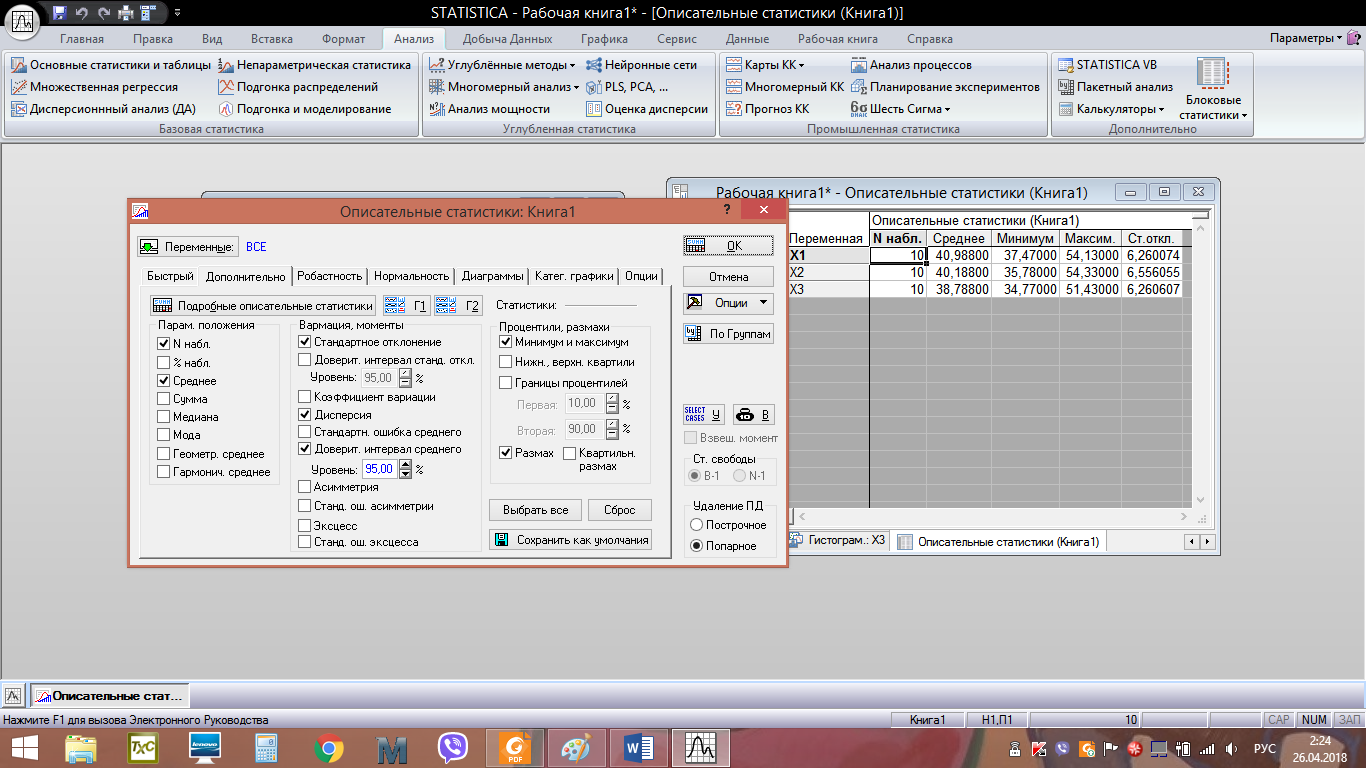

Нажмем ОК. На экране появится окно с описательными статистиками для переменных.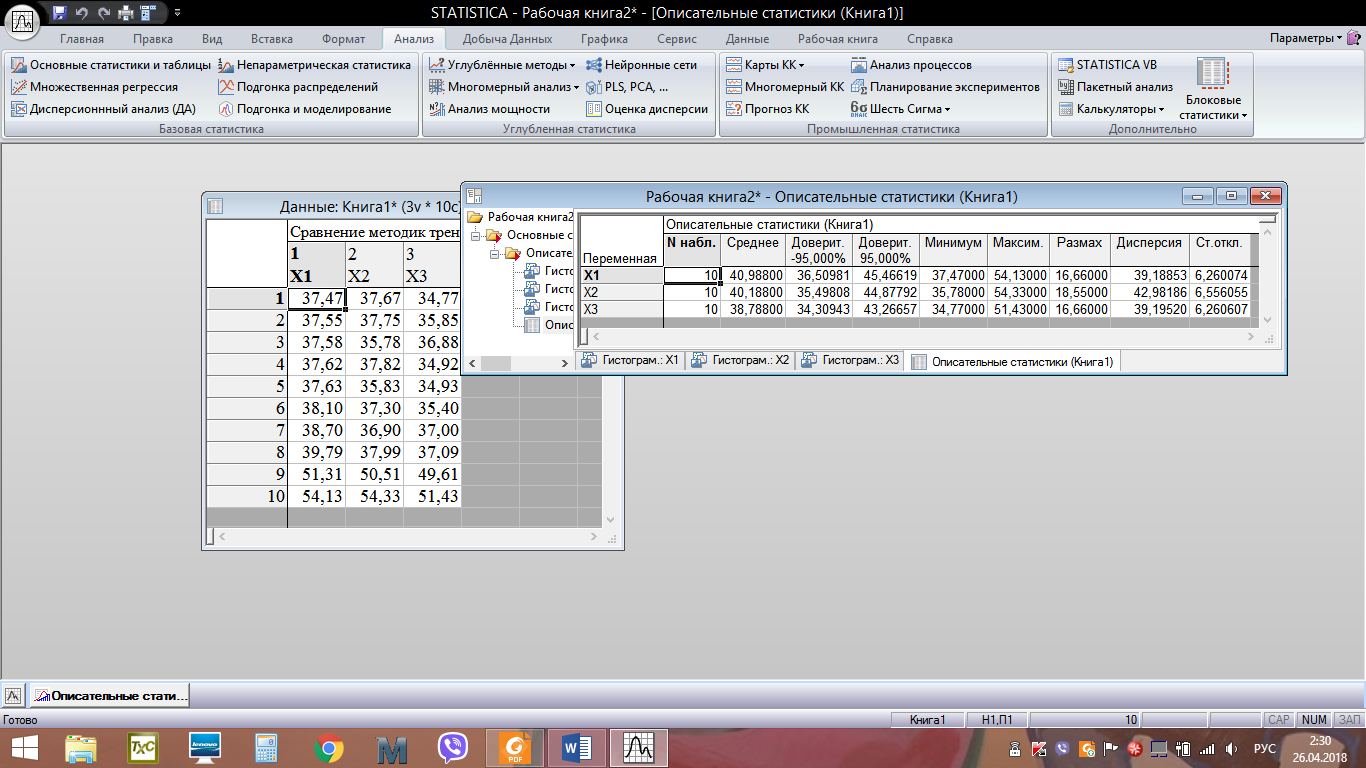

10. Выдвигаем статистические гипотезы:

- нулевая гипотеза Н0 – между выборками Х1, Х2, Х3 существуют лишь случайные различия в спортивном результате на дистанции 15 км;

- альтернативная гипотеза Н1 - между выборками Х1, Х2, Х3 существуют неслучайные различия в спортивном результате на дистанции 15 км;

11. Для использования Н-критерия Краскела-Уоллиса необходимо данные трех выборок расположить в одном столбце и добавить группирующую переменную, значения которой будут кодом, отражающим принадлежность данных к первой, второй и третьей выборке. Поскольку объем выборок составляет по 10 единиц наблюдения, то для совмещения данных в один столбец нужно увеличить высоту таблицы до 30 строк. Поэтому добавим еще 20 строк. Для этого выберем на панели инструментов вкладку Вставка – группу Наблюдения – команду Добавить.

12. В окне Добавить наблюдения укажем число добавляемых строк 20, и место вставки после 10 строки. Нажимаем ОК. Получится таблица 330. Затем необходимо выделить мышью данные группы Х2 и с помощью контекстного меню вырезать их – Вырезать и вырезанный фрагмент вставить после 10 строки в первый столбец Х1. Аналогично необходимо выделить мышью данные группы Х3, вырезать их и вставить после 20 строки в первом столбце Х1. Переименуем первый столбец в Результаты.

Второй столбец будет содержать кодирующие значения независимой (группирующей) переменной. Для этого во второй столбец введем напротив значений группы Х1 (1-10 строки) Х1, напротив группы Х2 (11-20 строки) – Х2, а напротив группы Х3 (21-30 строки) – Х3. Здесь можно использовать автозаполнение, как в Excel. Теперь пакет STATISTICA сможет распознать, где находятся данные экспериментальной и контрольной группы. Переименуем второй столбец в Группы. Фрагмент полученной таблицы представлен на следующем рисунке: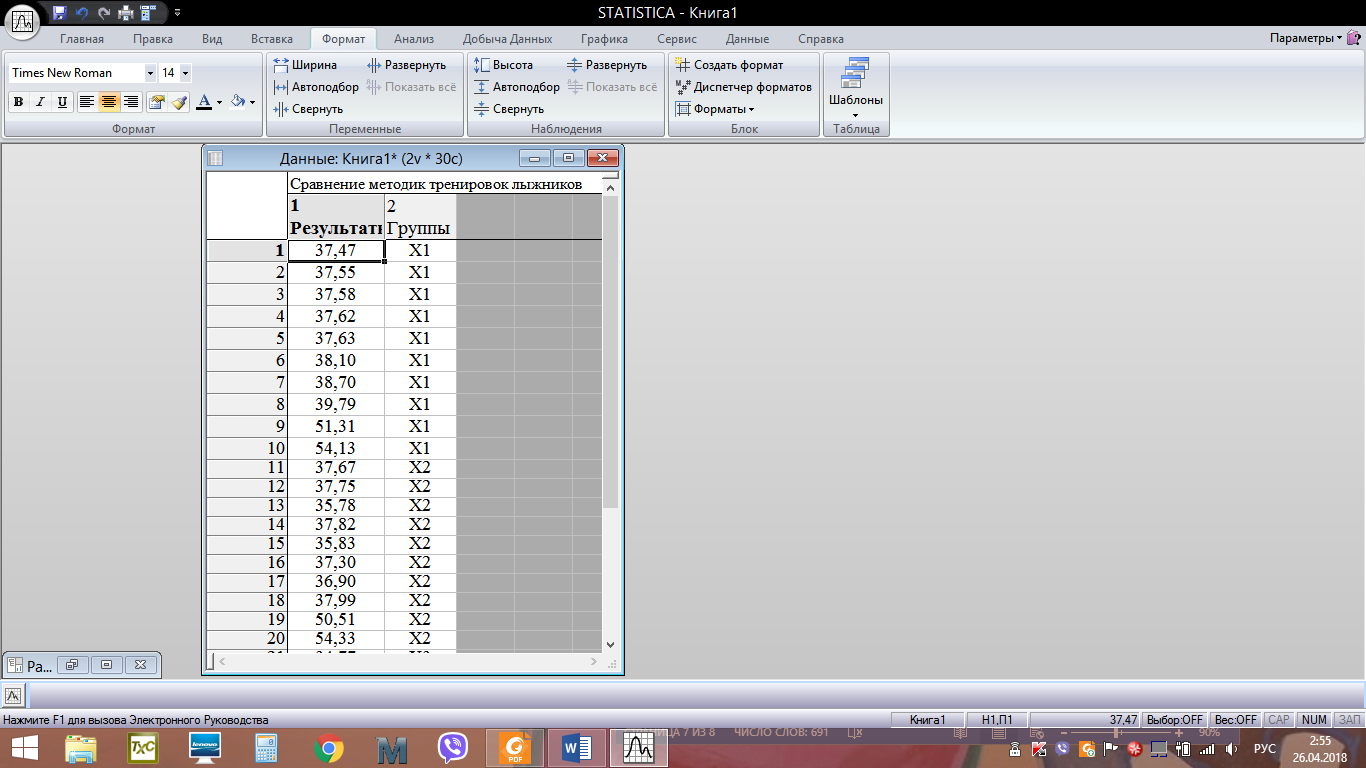

Сохраним файл под именем Сравнение методик тренировок лыжников.

13. На вкладке Анализ выберем Непараметрическая статистика. На экране появится окно Непараметрическая статистика, в котором необходимо выбрать пункт Сравнение нескольких независимых групп и нажать ОК.

14. В окне ДА Краскела-Уоллиса и медианный тест необходимо нажать на кнопку Переменные.

15. В окне Выберите группирующую переменную и зависимые переменные необходимо выбрать: зависимые переменные – Результаты, группирующие переменные – Группы. Нажать ОК.

16. В окне ДА Краскела-Уоллиса и медианный тест нажмем на кнопку Коды и далее в возникшем окне Выберите коды для группирующей переменной нажмите Все. В поле Группы появятся переменные Х1, Х2, Х3. Нажмем ОК.

17. В окне ДА Краскела-Уоллиса и медианный тест нажмем на кнопку ДА Краскела-Уоллиса и медианный тест. Появится окно с анализом данных. Программа рассчитывает две таблицы: Ранговый ДА Краскела-Уоллиса и Медианный тест.

18. Результаты расчетов выведены в три строки для каждой независимой переменной. Чем больше сумма рангов группы, тем выше значения этой группы по данной зависимой переменной. Видно, что спортсмены первой группы значительно отличаются от спортсменов второй и третьей группы по результату на дистанции 15 км.

Расчетное значение критерия Нрасч=6,815 больше Нкритич=5,991 при уровне значимости =0,05 (Нкритич приняли равным 2 при числе степеней свободы k и уровне значимости =0,05). Это позволяет принять альтернативную гипотезу о том, что между выборками Х1, Х2, Х3 существуют неслучайные различия. Альтернативная гипотеза может быть принята также по уровню значимости, равному 0,033, что ниже критического.

Таким образом, существует связь между используемыми методами тренировок и средними спортивными результатами в группах.

19. Выведем диаграмму размаха по группам, нажав кнопку Диаграмма размаха в окне ДА Краскела-Уоллиса и медианный тест.

Наибольшее отличие наблюдается у спортсменов, тренировавшихся по традиционной методике, по отношению к спортсменам второй и третьей группы, тренировавшимся по методикам Иванова и Петрова соответственно. Можно сделать обоснованный вывод о том, что использование методик Иванова и Петрова позволяет улучшить средний результат в группах лыжников на дистанции 15 км.

20. Рассмотрим таблицу Медианный тест. Данный метод основан на том, что для всех независимых выборок вычисляют общую медиану, затем подсчитывают, какое количество измеряемых величин находится ниже и выше медианы. Это приводит к построению таблицы, содержащей 2k полей, которую затем подвергают тесту 2. Однако эффективность медианного теста не очень высока.