КР. КР Вар1Физика. Пример решения задачи 1
 Скачать 240.17 Kb. Скачать 240.17 Kb.
|
|
Вариант 1 Радиус-вектор материальной точки изменяется со временем по закону: 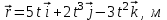 , где векторы , где векторы 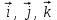 являются ортами декартовой системы координат. Какую работу совершила равнодействующая сила за вторую секунду движения, если масса материальной точки составляет 0,1 кг? являются ортами декартовой системы координат. Какую работу совершила равнодействующая сила за вторую секунду движения, если масса материальной точки составляет 0,1 кг?Пример решения задачи 1 Радиус-вектор материальной точки изменяется со временем по закону: 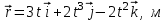 , где векторы , где векторы 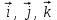 являются ортами декартовой системы координат. Какую работу совершила равнодействующая сила за вторую секунду движения, если масса материальной точки составляет 0,2 кг? Какую мощность развивает равнодействующая сила в конце второй секунды движения? являются ортами декартовой системы координат. Какую работу совершила равнодействующая сила за вторую секунду движения, если масса материальной точки составляет 0,2 кг? Какую мощность развивает равнодействующая сила в конце второй секунды движения?
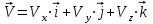 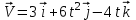 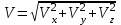 Отсюда квадрат скорости в конце первой и второй секунд: 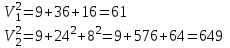 Работа равнодействующей силы равна: 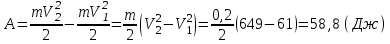 М 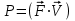 ощность найдем, как скалярное произведение силы на скорость ощность найдем, как скалярное произведение силы на скоростьСилу определим из второго закона Ньютона 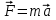 Ускорение – это производная от скорости по времени: 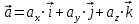 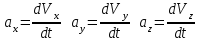 Отсюда ускорение 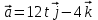 м/с2 м/с2Сила, действующая на тело: 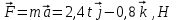 М 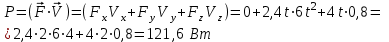 ощность в конце второй секунды: ощность в конце второй секунды:Ответ: А(1,2) = 58,8 Дж, Р(2)=121,6 Вт Шар массой 1 кг и радиусом 0,1 м находится на вершине пологой горки высотой 0,5 м. Шар без начальной скорости скатывается с горки и на горизонтальном участке пути сталкивается с покоящимся шаром массой 2 кг и радиусом 0,1 м. Удар абсолютно упругий, прямой, центральный. Какую скорость приобретет второй шар после удара? Потерями на трение пренебречь. Пример решения задачи 2 Сплошной однородный диск массой 0,1 кг и радиусом 0,1 м начинает скатываться с пологой горки высотой 0,3 м, плавно переходящей в горизонтальный участок. На горизонтальном участке диск сталкивается с другим вертикально стоящим сплошным однородным диском радиусом 0,1 м и массой 0,2 кг. Удар абсолютно упругий, прямой, центральный. Какую скорость будет иметь второй диск после соударения? Потерями на трение пренебречь.
Кинетическая энергия диска складывается из кинетической энергии поступательного движения диска с горки и вращательного движения диска вокруг центра масс. Используя теорему Кенига, запишем: 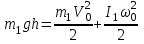 Момент инерции сплошного диска относительно оси, проходящей через центр масс, 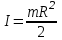 , а угловая скорость связана с линейной скоростью соотношением: , а угловая скорость связана с линейной скоростью соотношением: 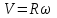 Подставляем все в закон сохранения энергии 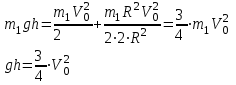 Скорость налетающего диска 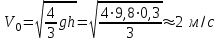 Для нахождения скорости второго диска воспользуемся законами сохранения энергии и импульса для абсолютно упругого удара. Закон сохранения импульса в проекции на горизонтальную ось 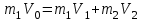 Закон сохранения энергии учитывает, что при абсолютно упругом ударе сохраняется кинетическая энергия, причем движутся одинаковые по размеру диски. В момент соударения учитываем кинетическую энергию поступательного движения дисков 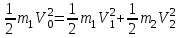 Сократим общие множители и перенесем в левую часть слагаемые при m1 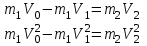 Во втором уравнении распишем разность квадратов и воспользуемся равенством из первого уравнения 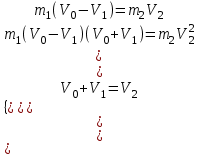 Выразив скорость V1 из полученного уравнения, подставим ее в закон сохранения импульса: 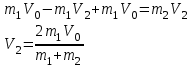 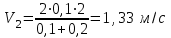 Ответ: V2 = 1,33 м/с, в направлении оси Х. Две концентрические непроводящие сферы радиусами R и 2R заряжены с поверхностной плотностью зарядов 1 и 2 соответственно. Найти силу (модуль и направление), действующую на электрон, находящийся в точке r1 = 3R от центра. Какая работа будет совершена при перемещении электрона из этой точки в точку r2 = 4R? Принять R = 0,1 м, 1 = 5 нКл/м2, 2= 5 нКл/м2. Пример решения задачи 3 Два очень длинных непроводящих концентрических (с общей осью) цилиндра радиусами R и 2R заряжены с поверхностной плотностью зарядов 1 и 2 соответственно. Найти силу (модуль и направление), действующую на электрон, находящийся в точке r1 = 3R от оси цилиндров. Какую скорость приобретет первоначально покоившийся электрон, переместившись в точку r2 = 6R от оси цилиндров? Принять R = 0,1 м, 1 = 1 нКл/м2, 2 = 1 нКл/м2.
Чтобы найти напряженность поля, созданного системой цилиндров, воспользуемся теоремой Гаусса: 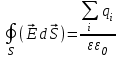 . .В качестве гауссовой поверхности выберем цилиндр радиуса rиобразующейl, соосный с заряженными цилиндрами. Поскольку исследуемые точки находятся снаружи заряженных цилиндров, то радиус гауссовой поверхности r>2R. В силу того, что линии напряженности имеют радиальное расположение, поток вектора напряженности через торцы построенного цилиндра равен нулю. Поток вектора напряженности через боковую поверхность 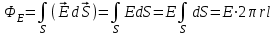 Заряд, попавший внутрь гауссовой поверхности равен 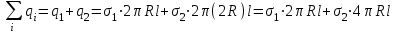 Величина вектора напряженности на расстоянии r 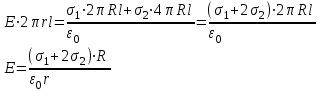 Подставим данные задачи для точкиr1 Подставим данные задачи для точкиr1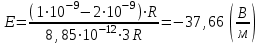 Знак «минус» означает, что вектор напряженности направлен против оси Х. Сила, действующая на электрон, помещенный в эту точку 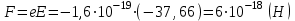 Сила направлена по оси Х от поверхности цилиндров. Чтобы найти скорость электрона, воспользуемся теоремой о кинетической энергии 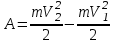 , где первоначальная скорость V1=0, а V2 является искомой скоростью . Движение электрона совершается под действием электрической силы по направлению оси Х. Работа электрического поля положительна и равна , где первоначальная скорость V1=0, а V2 является искомой скоростью . Движение электрона совершается под действием электрической силы по направлению оси Х. Работа электрического поля положительна и равна 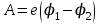 Разность потенциалов 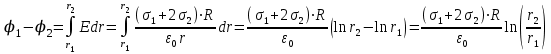 Подставляем данные задачи 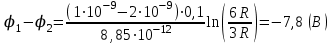 Работа электрического поля равна 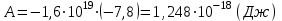 Скорость, приобретенная электроном 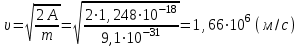 Ответ: 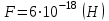 , направлена по оси Х от поверхности цилиндров. , направлена по оси Х от поверхности цилиндров. 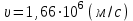 . .В изображённой на рис.1 электрической цепи, каждый резистор может поглощать максимальную тепловую мощность 10 Вт. Сопротивление резисторов R1= 100 Ом, R2= 200 Ом, R3= 20 Ом. Каково максимальное значение силы тока I, который можно пропустить по данной цепи, при котором ни один из резисторов не будет повреждён? 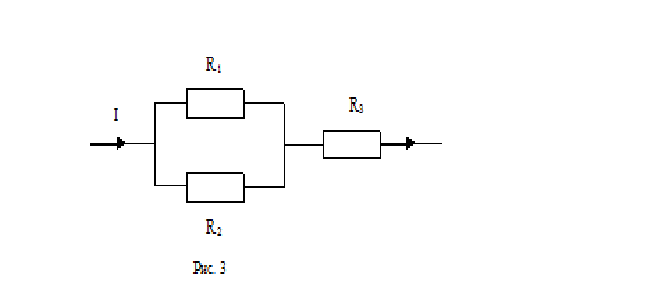 Рис. 1 5 Бесконечно длинный провод с током I=100 А изогнут так, как это показано на рисунке. В плоскости, в которой лежит изогнутый провод, пролетает электрон по направлению к точке О со скоростью ν =105 м/с. Определить величину и направление силы Лоренца, действующую на электрон, в точке О, если расстояние d=5 см. Рис.1 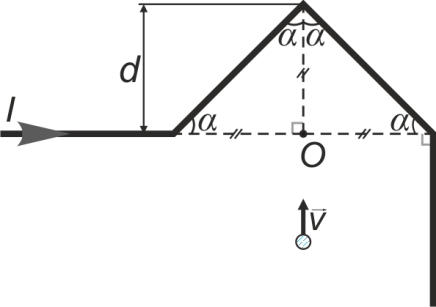 Пример решения задачи 5. Бесконечно длинный провод с током I=80 А изогнут так, как это показано на рисунке 8. В плоскости, в которой лежит изогнутый провод, пролетает электрон по направлению к точке О со скоростью υ=105 м/с. Определить величину и направление силы Лоренца, действующую на электрон, в точке О, если радиус дуги окружности R=10 см. Решение. Магнитную индукцию 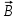 в точке O найдём, используя принцип суперпозиции магнитных полей в точке O найдём, используя принцип суперпозиции магнитных полей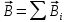 . В нашем случае провод можно разбить на три части (рис. 9): два прямолинейных провода (1 и 3), одним концом уходящие в бесконечность, и дугу полуокружности (2) радиуса R. . В нашем случае провод можно разбить на три части (рис. 9): два прямолинейных провода (1 и 3), одним концом уходящие в бесконечность, и дугу полуокружности (2) радиуса R. рис.9 Тогда 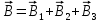 , ,где B1, B2 и B3 - магнитные индукции в точке O, создаваемые током, текущим соответственно на первом, втором и третьем участках провода. Так как точка O лежит на оси провода 1, то B1=0 и тогда 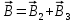 . .Учитывая, что векторы B2 и B3 направлены в соответствии с правилом буравчика перпендикулярно плоскости чертежа от нас, то геометрическое суммирование можно заменить алгебраическим: 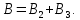 Магнитную индукцию B2 найдём, воспользовавшись выражением для магнитной индукции в центре кругового тока: 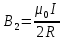 . .В нашем случае магнитное поле в точке O создаётся лишь половиной такого кругового тока, поэтому 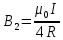 . .Магнитную индукцию B3 найдём, воспользовавшись соотношением магнитной индукции для отрезка провода с током: 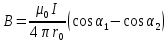 . .В нашем случае 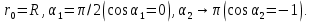 Тогда Тогда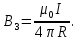 Используя найденные выражения для B2 и B3, получим Используя найденные выражения для B2 и B3, получим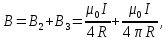 или или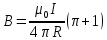 . .Проверим, дает ли правая часть равенства единицу магнитной индукции (Тл): 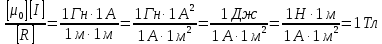 . .Здесь мы воспользовались определяющей формулой для магнитной индукции: 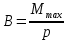 . .Тогда 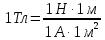 . .Выразим все величины в единицах СИ и произведём вычисления: 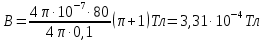 , ,или 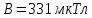 . .Найдем силу Лоренца, действующую на электрон в момент его нахождения в точке О и определяемую по формуле 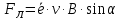 . .Т.к. α=90° (вектор υ лежит в плоскости чертежа, а вектор B перпендикулярен плоскости чертежа), то 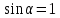 . Т.к. заряд электрона отрицателен, то сила Лоренца будет направлена вверх на рис. 9. И . Т.к. заряд электрона отрицателен, то сила Лоренца будет направлена вверх на рис. 9. И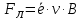 . .Проверим, дает ли правая часть равенства единицу силы (Н): 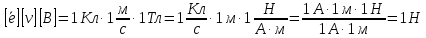 . .Тогда выразим все величины в единицах СИ и произведём вычисления: 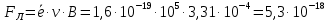 Н. Н.Ответ: 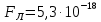 Н. Н.В магнитном поле с индукцией, изменяющейся со скоростью 2 млТл/с, находится соленоид. Ось соленоида с вектором магнитной индукции составляет угол α=30°. Диаметр витков соленоида составляет 10 см, а их число - 100. Сопротивление соленоида 20 Ом. Определить выделившуюся на соленоиде теплоту за время t=5 с. На вертикальной пружине закреплена горизонтальная платформа массой 700 г. Платформу вывели из положения равновесия и в системе возникли колебания с частотой 5,5 Гц. Записать уравнение колебаний, которые возникнут в системе, если на платформу положить груз массой 600 г, отвести платформу из положения равновесия на 6 см и плавно отпустить. Построить график скорости платформы за время, равное двум периодам колебаний. Материальная точка участвует одновременно в трех колебаниях, происходящих по одной прямой и выраженных уравнениями: X1 = 3 Cost, см. X2= 3 Cos( t + π / 3 ), см. X3= 3 Sin( t + 7 π / 6 ), см. Постройте векторную диаграмму сложения заданных колебаний и запишите уравнение результирующего колебания с числовыми коэффициентами. Пример 3 решения задачи 4 Материальная точка участвует одновременно в двух взаимноперпендикулярных гармонических колебаниях, уравнения которых 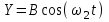 и и 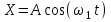 , где A=1см, В=2см , где A=1см, В=2см 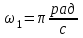 , ,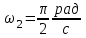 , т.е. , т.е. 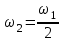 . .Найти уравнение траектории точки. Построить траекторию с соблюдением масштаба и указать направление движения точки. Решение задачи В данном случае колебания происходят с разными частотами, кратными 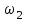 . Чтобы определить траекторию точки, исключим время из уравнения. Заметив, что . Чтобы определить траекторию точки, исключим время из уравнения. Заметив, что 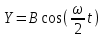 , применим формулу косинуса половинного угла , применим формулу косинуса половинного угла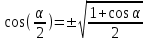 Используя это соотношение и отбросив размерности X и Y, можно написать: 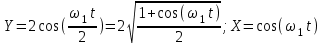 откуда 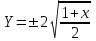 или или 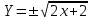 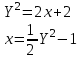 Уравнение представляет собой уравнение параболы, ось которой совпадает с осью ОХ. Как показывают уравнения, амплитуда колебаний точки по оси ОХ равна 1, а по оси ОY = 2. Следовательно, абсциссы всех точек траектории заключены в пределах от -1 до 1, а ординаты от -2 до 2. Для построения траектории найдем по уравнению значения Y, соответствующие ряду значений X, удовлетворяющих условию X⩽1.
Начертив координатные оси (рис 7.3.5) и выбрав единицу длины – сантиметр, построим точки. Соединив их плавной кривой, получим траекторию результирующего колебания точки. Она представляет собой часть параболы, заключенной внутри прямоугольника амплитуд (фигура Лиссажу). Из уравнения находим, что период колебаний 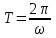 точки по горизонтальной оси точки по горизонтальной оси 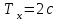 , а по вертикальной оси , а по вертикальной оси 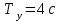 . Следовательно, когда точка совершит одно полное колебание по оси OX, она совершит только половину полного колебания по оси OY. В начальный момент (t = 0) имеем: X = 1, Y = 2 (точка находится в положении А). При t = 1с получим X=-1 Y=0 (точка находится в вершине параболы). При t=2c получим X=1 и Y=-2 (точка находится в положении D). После этого она будет двигаться в обратном направлении. . Следовательно, когда точка совершит одно полное колебание по оси OX, она совершит только половину полного колебания по оси OY. В начальный момент (t = 0) имеем: X = 1, Y = 2 (точка находится в положении А). При t = 1с получим X=-1 Y=0 (точка находится в вершине параболы). При t=2c получим X=1 и Y=-2 (точка находится в положении D). После этого она будет двигаться в обратном направлении.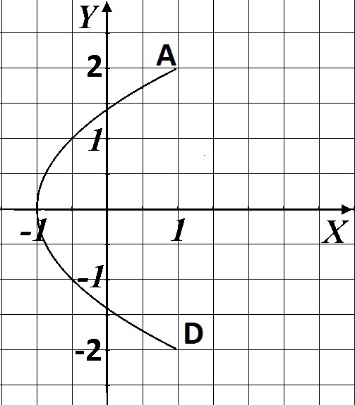 Рис.7.3.5 |

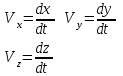

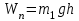 . Когда диск скатится с горки, его потенциальная энергия полностью перейдет в кинетическую энергию,
. Когда диск скатится с горки, его потенциальная энергия полностью перейдет в кинетическую энергию, 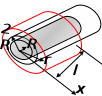
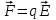 ,
,