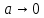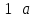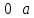дискретка. Пример (1). Пример выполнения задания
 Скачать 98.02 Kb. Скачать 98.02 Kb.
|
|
Пример выполнения задания. Задана формула F = x̅ → y̅ z / (y ∼ z̄) ∨ x y̅ z. 0) Расставим скобки в формуле F. Возьмем в скобки конъюнкции, затем остальные подформулы слева направо. (F) = ((x̅ → (y̅ z)) / (y ∼ z̄)) ∨ (x y̅ z). Далее при преобразовании формул для упрощения записи мы будем опускать скобки вокруг конъюнкций. 1) Построим таблицу истинности функции по формуле (F).  2) Построим матрицу Грея функции f(x, y, z) по таблице истинности. Отметим на матрице наборы, на которых f(x, y, z)=1. 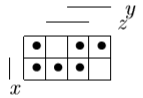 3) Получим ДНФ' по формуле (F) разложением по переменным. Применим к подформуле (x̅ → y̅z) / (y ∼ z̄) разложение Шеннона по переменной y (она встречается чаще, чем переменная x и так же часто, как переменная z). (F) = ((x̅ → y̅ z) / (y ∼ z̄)) ∨ x y̅ z = = y[(x̅ → 1̅ z) / (1 ∼ z̄)] ∨ y̅[(x̅ → ōz) / (0 ∼ z̄)] ∨ x y̅ z = [применим свойства 0 и 1 для конъюнкции] = y[(x̅ → 0)/(1 ∼ z̄)] ∨ y̅[(x̅ → z) / (0 ∼ z̄)] ∨ x y̅ z = [выведем свойства 0 и 1 для импликации и эквивалентности
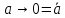 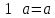 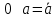 и упростим выражение] = y[x / z̄] ∨ y̅ [(x̅ → z) / z] ∨ x y̅ z = [разложим коэффициенты при y и y̅ по переменной z] = y [z (x / 1̅) ∨ z̄ (x / ō)] ∨ y̅ [z ((x̅ → 1) / 1) ∨ z̄ ((x̅ → 0) / 0)] ∨ x y̅ z = = y [z (x / 0) ∨ z̄ (x / 1)] ∨ y̅ [z ((x̅ → 1) / 1) ∨ z̄((x̅ → 0) / 0)] ∨ x y̅ z = [выведем свойства 0 и 1 для импликации и штриха Шеффера и упростим выражение] = y [z1 ∨ z̄ x̅] ∨ y̅ [z(1 / 1) ∨ z̄(x / 0)] ∨ x y̅ z = = y [z ∨ z̄ x̅] ∨ y̅ [z 0 ∨ z̄1] ∨ x y̅ z = [используем свойства 0 и 1 и закон дистрибутивности] 4) Построим матрицу Грея по ДНФ'. 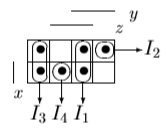 5) Получим ДНФ'' по формуле (F) подстановкой кратчайших ДНФ элементарных функций. Заменим штрих Шеффера a/b КратДНФ при a = x̅ → y̅ z, b = y ∼ z̄: 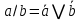 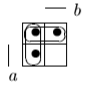 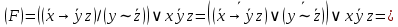 [заменим инверсию импликации на не импликацию и инверсию эквивалентности на дизъюнкцию с исключением] = (x̅ ↪ y̅ z) ∨ (y ⊕ z̄) ∨ x y̅ z = [найдем КратДНФ не импликации и дизъюнкции с исключением  и подставим их в формулу] 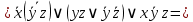 [применим законы де Моргана, дистрибутивности, ассоциативности] 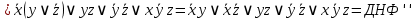 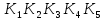 4') Построим матрицу Грея по ДНФ''. 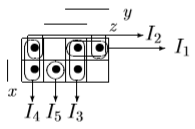 6) Построим сокращенную ДНФ по матрице Грея. Выделим все максимальные интервалы, они зададут конъюнкции сокращенной ДНФ. 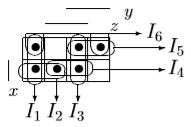 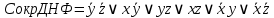 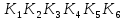 7) Преобразуем сокращенную ДНФ в совершенную ДНФ.   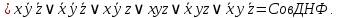 8) Построим кратчайшую ДНФ по матрице Грея. Выделим на матрице минимальное число максимальных интервалов, образующих достаточное множество, и по нему построим кратчайшую ДНФ. 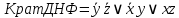 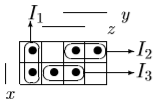 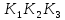 7') Преобразуем кратчайшую ДНФ в совершенную ДНФ. 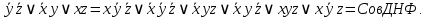 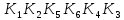 Здесь конъюнкциям присвоены номера из совершенной ДНФ задачи 7), сравнение показывает, что совершенные ДНФ совпали. 4'') Построим матрицу Грея по совершенной ДНФ. Каждая полная конъюнкция задается точкой, которая на матрице обозначена номером конъюнкции в совершенной ДНФ. 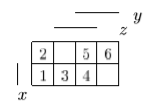 Вывод. Матрицы Грея, полученные при решении задач 2), 4), 4'), 4''), совпадают, следовательно, ошибок при выполнении контрольной работы нет (кроме, может быть, неверной расстановки скобок). |