МТУСИ Информатика Лабораторная работа №10. Лабораторная работа №10 по информатике(Поляков Н.С. группа БИН20. Примеры решения содержательных задач, использующие алгоритмы разветвляющихся структур
 Скачать 463.79 Kb. Скачать 463.79 Kb.
|
|
Федеральное агентство связи Ордена трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования «Московский технический университет связи и информатики» Факультет "Сети и системы связи" Отчет по лабораторной работе №10 по дисциплине «Информатика» на тему: «Примеры решения содержательных задач, использующие алгоритмы разветвляющихся структур» Выполнил: студент группы Проверил: _________________ Москва, 2020 Структура отчета: Титульный лист………………………………………………………………………………………………………………………..1 Структура отсчета……………………………………………………...................................................................2 Цель работы, вопросы принадлежащие изучению и общее здание……..................................3 Индивидуальное задание……….…................................................................................................5 Формализация и уточнение задачи….………................................................................................5 Разработанные схемы 5 процедур........……….............................................................................6 Разработанные программные коды 5-ти процедур…...............................................................9 Получены следующие результаты выполнения проекта...............................................…..…..10 Доказательство правильности результата...........................................….. ...............................11 Цель работы: развитии навыков разработки решения содержательных задач, основанных на программировании алгоритмов разветвляющихся структур, формализации таких задач и создании проектов, использующих алгоритмы разветвляющихся структур и сложные логические выражения. Вопросы, подлежащие изучению Логический тип данных, операции отношения и логические операции. Логические выражения и их использование в разветвляющихся программах. Программирование стандартных, усеченных и вложенных алгоритмических структур разветвления. Операторы ветвления и варианты их реализации. Вычисление значений условных функций. Формализации содержательных задач, использующих разветвляющиеся структуры Общее задание на разработку приложения Изучите вопросы формализации, алгоритмизации и программирования алгоритмов при решении содержательных задач, использующих разветвляющиеся структуры. Выберите вариант задания из табл. 10.3-1. Выполните формализацию задачи, для которой необходимо: нарисовать вручную рисунок; выделить на рисунке заданную область; для выделенной области определить и записать логическую условную функцию от двух переменных x и y (где [x,y] координаты точки), функцию, принимающую логическое значение false (0) или true (1), в зависимости от попадания или непопадания точки с координатами X, Y в выделенную область рисунка; Разработайте: две схемы алгоритмов и два программных кода функций решения задачи согласно вашему индивидуальному заданию: использующие стандартное разветвление и сложное логическое выражение; использующие вложенные разветвления только с помощью операций отношения, без применения логических операций и сложных логических выражений; программный код функции ввода исходных данных; программный код функции вывода результатов. программный код главной функции main(), которая вызывает описанные выше функции для решения поставленной задачи. (Схемы алгоритмов должны быть разработаны средствами Visio, а программные коды функций согласно этим схемам средствами С++). Создайте консольный проект, содержащий 3 раздельно откомпилированных файла: файл, содержащий функцию ввода исходных данных и функцию вывода результатов; файл с двумя разработанными согласно п.4. функциями; файл с главной функцией, которая должна содержать только операторы вызова пользовательских функций (ввода, 2 функции решения задачи разными способами и вывода, причем обмен данными между функциями должен осуществляется через параметры, без использования глобальных переменных. Подготовьте тесты для контрольного решения задачи. Выполните проект и получитерезультаты. Докажите правильность полученных результатовна заранее разработанных нескольких тестах. Лабораторная работа №10 «Примеры решения содержательных задач, использующие алгоритмы разветвляющихся структур» Индивидуальное задание
Формализация и уточнение задачи Построена «вручную», описанная в индивидуальном задании конструкция из фигур:  Определены уравнения, описывающие три фигуры – уравнения прямых AB, BC, CD, DA(1 фигура);A1B1, B1C1, C1D1, D1A1(2 фигура);A2B2, B2C2, C2D2, D2A2(3 фигура): (y1 -y2)*x+(x2-x1)*y+(x1*y2 - x2*y1) =0 A(0;2) и B(1;1) (2-1)x+(1-0)*y+(0*1-1*2)=x+y-2 y=2-x B(1;1) и C(-1;1) (1-1)*x+(-1-1)*y+(1*1-(-1)*1)=-2y+2 y=1 C(-1;1) и A(0;2) (1-2)*x+(0-(-1))*y+(-1*2-0*1)=-x+y-2 y=x+2 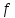 bool=( bool=(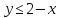 )&&(y )&&(y )&&(y )&&(yA1(0;1) и B1(1;0) (1-0)*x+(1-0)*y+(0*0-1*1)=x+y-1 y=1-x B1(1;0) и C1(-1;0) (0-0)*x+(-1-1)*y+(1*0-(-1)*0)=-2y y=0 C1(-1;0) и A1(0;1) (0-1)*x+(0-(-1))*y+(-1*1-0*0)=-x+y-1 y=x+1 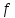 bool=( bool=(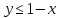 )&&( y )&&( y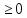 ) &&(y ) &&(yA2(0;0) и B2(1;-1) (0-(-1))*x+(1-0)*y+(0*(-1)-1*0)=x+y y=-x B2(1;-1) и C2(-1;-1) (-1-(-1))*x+(-1-1)*y+(1*(-1)-(-1)*(-1))=-2y-2 y=-1 C2(-1;-1) и A2(0;0) (-1-0)*x+(0-(-1))*y+(-1*0-0*-1)=-x+y y=x 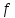 bool=( bool=( )&&( y )&&( y ) &&(y ) &&(yРазработаны схемы алгоритмов 5-ти процедур: Схема алгоритма функции ввода;  Рисунок 1- Схема алгоритма функции ввода 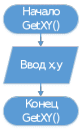 Схема алгоритма функции Resh1() вычисления условной функции решения задачи, использующей стандартное разветвление и сложное логическое выражение;  Рисунок 2- Схема алгоритма функции, использующей стандартное разветвление и сложное логическое выражение. 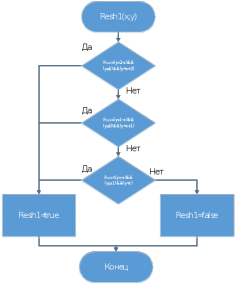 Схема алгоритма вывода функции;  Рисунок 3- Схема алгоритма функции вывода  Схема алгоритма функции пользователя Resh2() вычисления условной функции решения задачи, которая реализует вложенные разветвления только с помощью операций и сложных логических выражений;  Рисунок 4- Схема алгоритма функции, реализующей вложенные разветвления только с помощью операций отношения, без использования логических операций и сложных логических выражений.  Схема алгоритма главной функции;   Рисунок 5- Схема алгоритма главной функции вывода Рисунок 4- Схема алгоритма главной функции  Разработаны программные коды 5-ти процедур: //Файл с главной функцией #include #include using namespace std; int main() { float x, y; bool b, с;//признак попадания в область GetXY(x, y);//вызов функции ввода исх. данных cout << "Решение 1-й функции:"; b = Resh1(x, y);//вызов 1-й функции решения Put(b,x,y);//вызов функции вывода результатов cout << "Решение 2-й функции:"; с = Resh2(x, y);//вызов 2-й функции решения Put(с, x, y); system("PAUSE"); return 0; } //Файл с функцией ввода и вывода #include #include using namespace std; //определение функции ввода void GetXY(float& x, float& y) { setlocale(LC_ALL, "rus"); cout << "Введите координаты точки"< cin >> x >> y; } //определение функции вывода void Put(bool b) { setlocale(LC_ALL, "rus"); cout << "Точка с координатами "; if (b) cout << "попала в заданную точку"< else cout << "не попала в заданную область"< } //Файл с заголовком #pragma once void GetXY(float& x, float& y); void Put(bool, float, float); bool Resh1(float x, float y); bool Resh2(float x, float y); //Файл с функциями решения задачи #include #include //перевая-стандарт.разветв. с логическими операциями bool Resh1(float x, float y) { if (y<=2-x && y>=1 && y { return true; } else if (y <= 1 - x && y >= 0 && y < x + 1) //фигура 2 { return true; } else if (y <= - x && y >= -1 && y < x) //фигура 3 { return true; } else return false; //не входит } //вторая-вложенное развлетвление bool Resh2(float x, float y) { if (y<=2-x) //фигура 1... if(y>=1) if(y // if (y<=1-x) //фигура 2... if (y>= 0) if (y // if (y<=-x) //фигура 3... if (y>=-1) if (y // return false; //не входит } Получены следующие результаты выполнения проекта, Приведенные на рисунках 6-7 для тестовых данных точек, попадающих и непопадающих в заданную область  Рисунок 6- Результаты выполнения проекта для тестовых данных точки, попадающей в заданную область   Рисунок 7- Результаты выполнения проекта для тестовых данных точки, не попадающей в заданную область 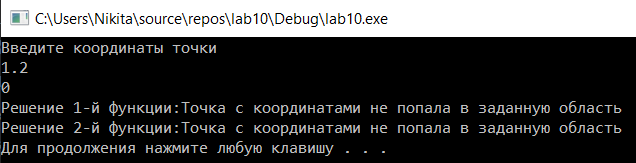 Доказательство правильности результата Разработаны с тестовые исходные данные для контрольного решения, проверяющее попадание и непопадание точки с различными координатами в заданную область, и получены результаты:
При тестовых данных результаты ручного расчета и вычисления на компьютере совпадают. | ||||||||||||||||
