Гидравлика практические работы. Примеры решения задач
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
Примеры решения задачПример 1.1. В закрытом резервуаре с нефтью плотностью ρ= 880 кг/м3 вакуумметр, установленный на его крышке, показывает рв= 1,18 · 104 Па (рис. 1). О 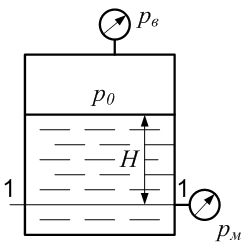 пределить показание манометра рм, присоединенного к резервуару на глубине Н = 6 м от поверхности жидкости, и положение пьезометрической плоскости. РешениеПроведем плоскость 1 - 1 на уровне присоединения манометра. В этой плоскости абсолютное давление в соответствии с основным уравнением гидростатики (2.1.3) равно: р1-1 = р0 + ρgH, Рис. 1. К примеру 1.1 где р0 — абсолютное давление на поверхности, равное ра — рв. Тогда р1-1 = ра — рв + ρgH. С другой стороны, так как манометр измеряет избыточное давление (рм=ри), то р1-1 = ра + рм . Приравняв два выражения для р1-1, найдем рм: рм = - рв+ ρgH = - 1,18·104 + 880·9,8·6 = 3,99·104 Па. Так как на поверхности жидкости давление меньше атмосферного, то пьезометрическая высота отрицательна:  м, м,и пьезометрическая плоскость расположена ниже поверхности жидкости на расстоянии 1,37 м. Пример 1.2. Найти избыточное давление в сосуде А с водой по показаниям многоступенчатого двухжидкостного ртутного манометра (рис. 2, стр. 337): h1 = 82 см; h2= 39 см; h3 = 54 см; h4 = 41 см; h5 = 100 см; ρв=103кг/м3; ρр=1,36·104 кг/м3. Р 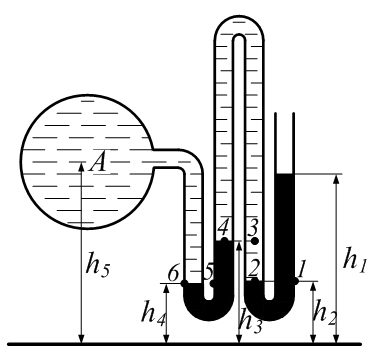 ешение Так как жидкость находится в равновесии, то давления в точке 1 и в точке 2 равны как давления в точках одного и того же объема однородной покоящейся жидкости, расположенных на одной горизонтали, т.е. р1 = р2. На том же основании р3 = р4, р5 = р6 . В то же время избыточное давление  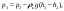 Рис. 2. Кпримеру 1.2 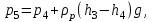 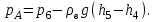 Исключив из этих соотношений промежуточные давления p2, p4, p6, получим: рА= ρрg[(h1 –h2) + (h3 – h4 )] — ρвg[(h3 - h2 ) + (h5 - h4)] = =1,36·104·9,8 (0,43+0,13) - 103·9,8 (0,15 + 0,59) = 67,4 кПа. Пример 1.3. Определить давление на забое закрытой газовой скважины (рис. 3), если глубина скважины Н = 2200 м, манометрическое давление на устье рм = 10,7 МПа, плотность природного газа при атмосферном давлении и температуре в скважине (считаемой неизменной по высоте) ρ = 0,76 кг/м3, атмосферное давление ра = 98 кПа. Решение Д  ля определения давления на забое газовой скважины воспользуемся барометрической формулой 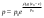 В нашей задаче р0 – абсолютное давление газа на устье скважины р0 = ра + рм = 9,8 · 103 + 10,7 · 106 = = 10,8 · 106 Па; ρ0 – плотность при давлении р0, а z0 – z = 2200 м. Из уравнения состояния газа следует, что Рис. 3. Кпримеру 1.3 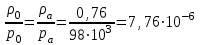 с2/м2, с2/м2,а показатель степени:  Тогда р = 10,8 · 106 · е 0,167 = 12,8 МПа. Пример 1.4. Вертикальная стенка (рис. 4) длиной l =3 м (в направлении, перпендикулярном плоскости чертежа), шириной b = 0,7 м и высотой H0= 2,5 м разделяет бассейн с водой на две части. В левой части поддерживается уровень воды H1 = 2 м, в правой — Н2 = 0,8 м. Найти величину опрокидывающего момента, действующего на стенку, а также определить, будет ли стенка устойчива против опрокидывания, если плотность материала стенки ρст = 2500 кг/м3. РешениеНайдем силу давления воды на стенку слева. Так как на поверхности давление атмосферное, то пьезометрическая плоскость совпадает с поверхностью жидкости  Рис. 4. Кпримеру 1.4 рт – ра = pg 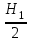 , ,Р1 = pg 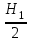 lН1= 103·9,8·2/(2·3·2)=58,8·103 Н = 58,8 кН. lН1= 103·9,8·2/(2·3·2)=58,8·103 Н = 58,8 кН.Координата центра давления lD1 = lт + J/lтs. Для прямоугольной стенки J= 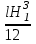 , тогда , тогда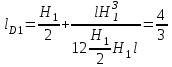 м. м.Точно так же справа: 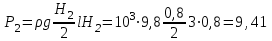 кН, кН, м. м.Опрокидывающий момент, т.е. момент сил давления жидкости относительно точки О (см. рис. 5.1.12):  Н·м. Н·м.Устойчивость против опрокидывания сообщает стенке момент силы тяжести относительно точки О: 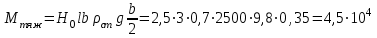 Н·м. Н·м.Так как Мтяж > Мопр, то стенка устойчива. Пример 1.5. Для слива жидкости из бензохранилищ имеется квадратный патрубок со стороной h = 0,3 м, закрытый крышкой, шарнирно закрепленной в точке О. Крышка опирается на торец патрубка и расположена под углом 45° (α = 45°) к горизонту (рис. 5). Определить (без учета трения в шарнире О и рамке В) силу Fнатяжения троса, необходимую для открытия крышки АО, если уровень бензина Н = 3 м, давление над ним, измеренное манометром, рм= 5 кПа, а плотность бензина ρ = 700 кг/м3 . Вес крышки не учитывать. 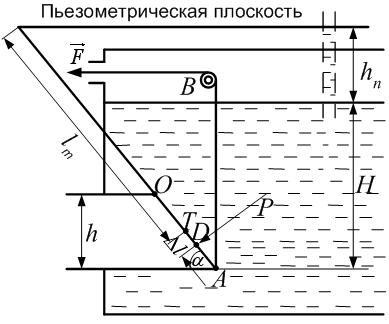 Рис. 5. Кпримеру 1.5 Решение Найдем силу давления на стенку АО. Рассматриваемой смоченной поверхностью является прямоугольная наклонная стенка высотой h/sinαишириной h, т.е. s = h2/sinα. Центр тяжести этой стенки находится на глубине h т= H - h/2, Δр = рм, т.е. 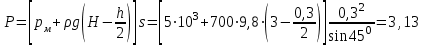 кН. кН.Найдем теперь расстояние между центром давления и центром тяжести крышки. 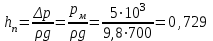 м. м.Тогда 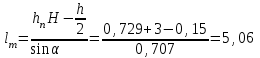 м. м.Момент инерции прямоугольной стенки относительно горизонтальной оси, проходящей через центр тяжести стенки: 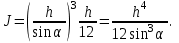 Тогда 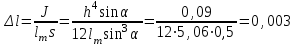 м. м.Найдем силу натяжения троса из уравнения моментов сил, взятых относительно оси шарнира О: 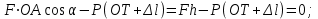  кН. кН.Примеры решения задачПример 1.6. Секторный щит радиуса Rи шириной В (рис. 6, стр. 341) перегораживает канал с жидкостью. Определить силу давления жидкости и направление ее действия. Решение 1. Вертикальная составляющая силы давления Рz = ρgVт.д, где Vт.д = πR2В/4 (пьезометрическая поверхность в этой задаче совпадает со свободной поверхностью жидкости в канале, так как на ней давление атмосферное). Сила Рzприложена в центре тяжести объема тела давления и направлена вверх, так как любая элементарная сила давления жидкости dPв любой точке щита дает при разложении вертикальную составляющую, направленную вверх. 2.Горизонтальная составляющая силы давления Рг = (рт – ра) sв = ρg  RB RBнаправлена слева направо (все dPнаправлены от жидкости к стенке). 3.Результирующая сила давления жидкости  направлена по радиусу к оси щита; угол ее наклона к горизонту определяется из выражения: cos α = Pг/P = 1/(2·0,93) = 0,53 Следовательно, α = 57° 27'. 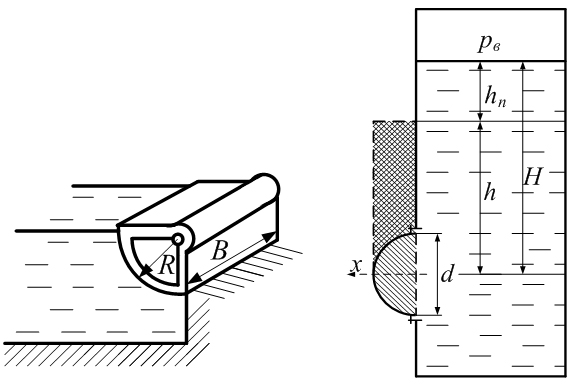 Рис. 6 Рис. 7 Пример 1.7. В боковой плоской стенке резервуара с реактивным топливом (ρ= 800 кг/м3 ) имеется круглый люк диаметром d = 0,5 м, закрытый полусферической крышкой (рис. 7). Высота жидкости в резервуаре над осью люка Н = 3 м, вакуум на ее свободной поверхности рв = 4,9 кПа. Определить горизонтальную и вертикальную составляющие силы давления жидкости на крышку люка, а также величину их равнодействующей и ее направление. Решение 1. Найдем положение пьезометрической плоскости, необходимой для определения объема тела давления. Так как на свободной поверхности жидкости — вакуум, пьезометрическая плоскость будет лежать ниже на расстоянии 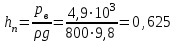 м. м.2. Определим вертикальную составляющую силы давления жидкости на крышку. Пьезометрическая плоскость лежит выше оси крышки на h = H - hп = 3 - 0,625 = 2,375 м, следовательно, сила давления направлена наружу. Для верхней половины крышки люка вертикальная составляющая направлена вверх, и ее величина определяется весом тела давления, заштрихованного на рис. 7 "справа вниз". Объем этого тела давления равен разности объемов полуцилиндра высотой hи четверти шара. Для нижней половины крышки вертикальная составляющая силы давления направлена вниз. Объем тела давления для этого случая равен сумме объемов полуцилиндра и четверти шара (на рис. 7 заштриховано "слева вниз"). Результирующая вертикальная сила равна разности этих двух сил, направлена вниз, и объем ее тела давления равен объему жидкости в крышке люка. Поэтому Pz=ρgVт.д = 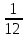 ρgπd3 = ρgπd3 =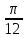 800·9,8·0,53 = 257 Н. 800·9,8·0,53 = 257 Н.Линия действия этой силы проходит через центр тяжести объема крышки люка на расстоянии от ее основания: 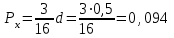 м. м.3.Определим горизонтальную составляющую силы давления жидкости на крышку. 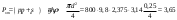 кН. кН.Сила направлена параллельно оси х, а линия ее действия лежит ниже этой оси, на  м. м.Определим равнодействующую сил давления:  кН. кН.Косинус угла αмежду осью х и линией действия этой силы: 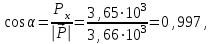 откуда α ≈ 4°. Пример 2.1. Определить, пренебрегая потерями напора, скорость течения нефти на расстоянии r от оси трубопровода радиусом R при помощи устройства (трубка Пито), показанного на рис. 1 Уровень жидкости в трубке А h1 = 1,2 м, в трубке В h2 = 1,35 м. 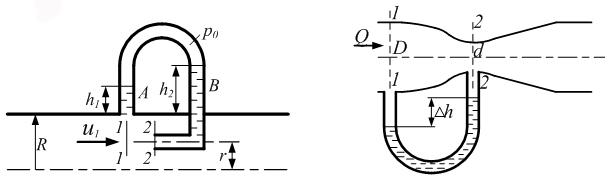 Рис. 1 Трубка Пито Рис. 19. Расходомер Вентури РешениеУчитывая, что h1-2 = 0 по условию, из уравнения Бернулли ( 19) для струйки, проходящей на расстоянии r от оси трубы имеем: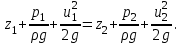 Так как трубопровод расположен горизонтально, то z1 = z2.Скорость в сечении 2 — 2 u2 = 0, поскольку жидкость в трубке B находится в состоянии покоя. Тогда  С учетом того, что давление в трубках и живых сечениях потока распределено по гидростатическому закону, получим: С учетом того, что давление в трубках и живых сечениях потока распределено по гидростатическому закону, получим: 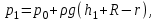 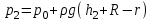 и 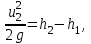 откуда  м/с. м/с.Пример 2.2. Найти при помощи устройства, показанного на рис. 19 (расходомер Вентури), объемный расход керосина (ρ = 850 кг/м3). Диаметр трубопровода D = 0,3 м; диаметр узкого сечения расходомера d = 0,1 м. Разность уровней ртути в дифманометре Δh = 0,025 м. Режим течения турбулентный. Потерями напора можно пренебречь. Решение Проведем живые сечения 1 - 1 и 2 – 2 и запишем для них уравнение неразрывности и уравнение Бернулли 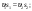  Так как труба горизонтальная, а потерями можно пренебречь, то z1=z2, h1-2=0. Приняв, кроме того α1=α2=1 и исключив из этих уравнений υ2, получим:  откуда 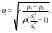 Разность давлений, измеренная дифманометром: 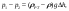 где ρРТ - плотность ртути. Следовательно  Пример 2.3. Определить полезную мощность насоса (рис. 20, стр. 350), перекачивающего бензин (ρ = 750 кг/м3) из резервуара A в резервуар В, если h1 = 1 м, h3 = 5 м, расход бензина Q = 10-3 м3/с, D = 0,1 м; d = 0,05. Потери во всасывающей линии равны 2 м, а в нагнетательной 5 м. Оба резервуара открытые. Решение Разность полных удельных энергий в сечениях непосредственно за насосом (2 - 2) и передним (1 - 1) представляет собой удельную энергию НН, сообщенную насосом жидкости, т.е. 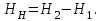 Тогда полезная мощность насоса 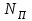 : :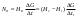 где ΔG- вес перекачанной жидкости за время Δt . 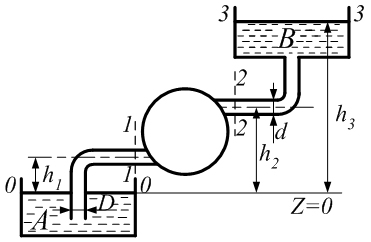 Рис. 20. Схема насосной установки Поскольку очевидно, что 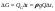 то 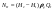 ( 1) ( 1)где Н1-Н2- напор создаваемый насосом Ннас. Для определения полных напоров Н1 и Н2 рассмотрим участки трубопровода между сечениями 0 - 0 и 1 - 1 (всасывающая линия), а также 2 – 2 и 3 - 3 (нагнетательная линия). Записав для каждого из этих участков уравнение Бернулли, имеем соответственно: 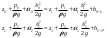 где z0 = 0, z1 = h1, z3 = h3 . Так как резервуары открыты, то p0 = p3 = pa. Площади свободных поверхностей резервуаров A и B велики по сравнению с площадями живых сечений труб. Поэтому можно принять υ0=υ3=0. Тогда  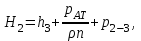 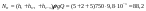 Вт. Вт.2.2. Гидравлический расчет простых напорных трубопроводов Примеры решения задач Пример 2.4. Насос (рис. 21) подает дизельное топливо (ρ = 840 кг/м3, ν = 5,5∙10-6 м2/с ) из нижнего резервуара в верхний с расходом Q = 16 дм3/с, давление на поверхностях жидкости в резервуарах одинаковое. Высота подъема топлива H = 20 м, Н1 = 3 м. На всасывающей линии (lв = 10 м, dв = 125 мм) установлены фильтр для светлых нефтепродуктов и задвижка, на нагнетательной линии (lн = 800 м, dн = 100 мм) эквивалентная длина местных сопротивлений оценивается в 5 % от ее реальной длины. Все трубы новые сварные. 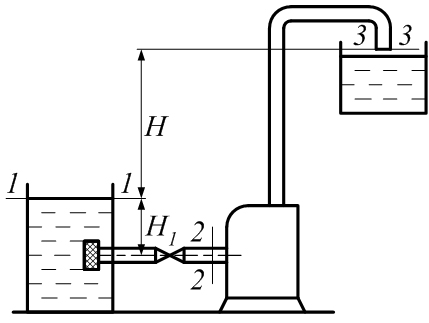 Рис. 21 Определить: 1) напор, создаваемый насосом, и его полезную мощность; 2) тип прибора (манометр или вакуумметр), установленный перед насосом в конце всасывающей линии. Решение 1. Для определения создаваемого насосом напора Hнас запишем уравнение баланса напоров для начального 1 - 1 и конечного 3 - 3 живых сечений потока: 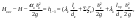 где индекс в относится к всасывающей, а н — к нагнетательной линии соответственно. 2. Найдём входящие в это уравнение неизвестные величины. Для всасывающей линии: 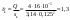 м/с; м/с; 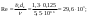 режим турбулентный. Установим зону сопротивления. По прил. 1 Δ = 0,05 мм. Тогда 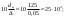 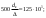 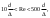 т.е. зона сопротивления — гидравлически шероховатые трубы. 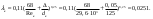 Определим значения коэффициентов местных сопротивлений (по прил. 2). Для фильтра ζф = 1,7, для задвижки ζз= 0,15; ∑ζв= 1,85. Для нагнетательной линии:   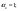 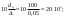 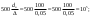 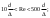 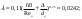 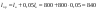 м. м.3. Из уравнения (2.2.14) имеем:  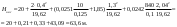 Попутно, сравнивая полученные значения входящих в уравнения величин, видим, что скоростной напор (0,21 м) по сравнению с H и h1-3 величина пренебрежимо малая (около 0,3 % от их суммы). 4. Определим полезную мощность насоса по ( 1): 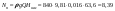 кВт. кВт.5. Определим тип прибора, установленный у насоса (в сечении 2 – 2). Для этого составим уравнение Бернулли для сечений 1 - 1 и 2 - 2. 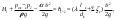 откуда 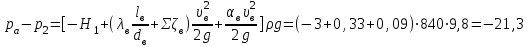 кПа. кПа.Если ра – р2 -величина отрицательная, то р2 > ра и ра – р2 = 21,3 кПа — давление избыточное. Следовательно, в сечении 2 - 2 установлен манометр. |
