Приведение матричной игры к задаче линейного программирования

• Название: Приведение матричной игры к задаче линейного программирования
• Дата: 08.01.2021
• Размер: 310.23 Kb.
• Имя файла: 571882.rtf
• Тип: Решение; #166362

">http://www.allbest.ru/

Тема: "Приведение матричной игры к задаче линейного программирования"

Игра т х п в общем случае не имеет наглядной геометрической интерпретации. Ее решение достаточно трудоемко при больших т и п, однако принципиальных трудностей не имеет, поскольку может быть сведено к решению задачи линейного программирования. Покажем это.

Пусть игра т х п задана платежной матрицей . Игрок А обладает стратегиями , игрок В — стратегиями . Необходимо определить оптимальные стратегии и , где - вероятности применения соответствующих чистых стратегий ;

игра линейный программирование матрица


Оптимальная стратегия удовлетворяет следующему требованию. Она обеспечивает игроку А средний выигрыш, не меньший, чем цена игры v, при любой стратегии игрока В и выигрыш, равный цене игры v, при оптимальной стратегии игрока В. Без ограничения общности полагаем v > 0, этого можно добиться, сделав все элементы . Если игрок А применяет смешанную стратегию против любой чистой стратегии игрока В, то он получает средний выигрыш, или математическое ожидание выигрыша (т.е. элементы j-того столбца платежной матрицы почленно умножаются на соответствующие вероятности стратегий и результаты складываются).

Для оптимальной стратегии все средние выигрыши не меньше цены игры v, поэтому получаем систему неравенств:
(1)
Каждое из неравенств можно разделить на число v > 0. Введем новые переменные:
(2)
Тогда система (1) примет вид:
(3)
Цель игрока А — максимизировать свой гарантированный выигрыш, т.е. цену игры v. Разделив на равенство , получаем, что переменные удовлетворяют условию: . Максимизация цены игры v эквивалентна минимизации величины 1/v, поэтому задача может быть сформулирована следующим образом: определить значения переменных , , так, чтобы они удовлетворяли линейным ограничениям (3) и при этом линейная функция
(4)
обращалась в минимум. Это задача линейного программирования. Решая задачу (3)—(4), получаем оптимальное решение оптимальную стратегию .

Для определения оптимальной стратегии следует учесть, что игрок В стремится минимизировать гарантированный выигрыш, т.е. найти . Переменные удовлетворяют неравенствам
(5)
которые следуют из того, что средний проигрыш игрока В не превосходит цены игры, какую бы чистую стратегию не применял игрок А.

Если обозначить
(6)
то получим систему неравенств:
(7)
Переменные удовлетворяют условию

Игра свелась к следующей задаче. Определить значения переменных , которые удовлетворяют системе неравенств (7) и максимизируют линейную функцию
(8)
Решение задачи линейного программирования (6), (7) определяет оптимальную стратегию . При этом цена игры

Составив расширенные матрицы для задач (3), (4) и (7), (8), убеждаемся, что одна матрица получилась из другой транспонированием:



Таким образом, задачи линейного программирования (3), ( 4) и (7), (8) являются взаимно-двойственными. Очевидно, при определении оптимальных стратегий в конкретных задачах следует выбрать ту из взаимно-двойственных задач, решение которой менее трудоемко, а решение другой задачи найти с помощью теорем двойственности.

Приведем примеры экономических задач, которые описываются игровыми моделями и могут быть решены методами линейного программирования.

Предприятие может выпускать три вида продукции , получая при этом прибыль, зависящую от спроса, который может быть в одном из четырех состояний ( ). Дана матрица ее элементы характеризуют прибыль, которую получит предприятие при выпуске i-той продукции с j-м состоянием спроса.

Определить оптимальные пропорции в выпускаемой продукции, гарантирующие среднюю величину прибыли при любом состоянии спроса, считая его неопределенным.
Таблица 1.

	3	3	6	8
	9	10	4	2
	7	7	5	4

Решение. Задача сводится к игровой модели, в которой игра предприятия А против спроса В задана платежной матрицей (втаблице). Прежде чем решать задачу, можно попытаться упростить игру, проведя анализ платежной матрицы и отбросив стратегии, заведомо невыгодные или дублирующие.

Так, вторая стратегия (второй столбец матрицы) является явно невыгодной для игрока В по сравнению с первой (элементы второго столбца больше элементов первого столбца), так как цель игрока В — уменьшить выигрыш игрока А. Поэтому второй столбец можно отбросить. Получим матрицу Р размера 3х3: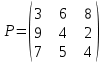

Таблица.

	3	6	8	3
	9	4	2	2
	7	5	4	4
	9	6	8	4 6

Определим нижнюю и верхнюю цены игры в таблице. Так как , то седловая точка отсутствует и оптимальное решение следует искать в смешанных стратегиях игроков:
и .
Обозначив и составим две взаимно-двойственные задачи линейного программирования
Задача 1 Задача 2






Решаем симплексным методом одну из задач, например, задачу 2, поскольку для нее первое базисное решение будет допустимым. Введем добавочные переменные и перейдем к уравнениям:

Оптимальное решение задачи 1: (2/27; 0;1/9; 1/2; 0; 17/27) причем Из соотношений (9) находим цену игры Оптимальную стратегию находим, используя:
т.е.
Следовательно, предприятие должно выпустить 40% продукции и 60% продукции , а продукцию не выпускать.

Оптимальная стратегия спроса определяется аналогично:
, т.е. = (0,2; 0; 0,8; 0)
(здесь учтено, что второй столбец исходной матрицы был отброшен как невыгодный). Таким образом, оптимальный спрос в 20% находится в состоянии и в 80% - в состоянии

При решении произвольной конечной игры размера т х п рекомендуется придерживаться следующей схемы:

1. Исключить из платежной матрицы заведомо невыгодные стратегии по сравнению с другими стратегиями. Такими стратегиями для игрока А (игрока В) являются те, которым соответствуют строки (столбцы) с элементами, заведомо меньшими (большими) по сравнению с элементами других строк (столбцов).

2. Определить верхнюю и нижнюю цены игры и проверить, имеет ли игра седловую точку. Если седловая точка есть, то соответствующие ей стратегии игроков будут оптимальными, а цена совпадает с верхней (нижней) ценой.

3. Если седловая точка отсутствует, то решение следует искать в смешанных стратегиях. Для игр размера т х п рекомендуется симплексный метод, для игр размера 2 х2, 2 х n, n х 2 возможно геометрическое решение.

На практике реализация оптимального решения в смешанных стратегиях может происходить несколькими путями. Первый состоит в физическом смешении чистых стратегий в пропорциях, заданных вероятностями .

Другой путь - при многократном повторении игры - в каждой партии чистые стратегии применяются в виде случайной последовательности, причем каждая из них — с частотой, равной ее вероятности в оптимальном решении.