Привод к тарельчатому питателю для формовочной земли
 Скачать 349.6 Kb. Скачать 349.6 Kb.
|
1.6 Расчет закрытой червячной передачи1) Определяем межосевое расстояние aw, мм: aw = 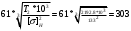 , ,где T2 = 2192.8 H*м; [σ] H = 133 H/мм2; 2) Выбираем число витков червяка z1: z1 = 2 3) Определяем число зубьев червячного колеса z2: z2 = z1*Uзп = 2*16 = 32 4) Определяем модуль зацепления m, мм: m = 1.6* aw // z2 = 1.6*303/32 = 15.15 ≈ 16 5) Определяем коэффициент диаметра червяка q: q ≈ 0.23* z2 = 0.23*32 = 7.36 ≈ 8 6) Определяем коэффициент смещения инструмента: x = (aw/m) - 0.5* (q+ z2) = (303/16) - 0.5* (8+32) = - 1.07 7) Определяем фактическое передаточное число и проверяем его отклонение ΔU от заданного U: Uф = z2/ z1 = 32/2 = 16 ΔUф = 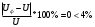 8) Определяем фактическое значение межосевого расстояния aw, мм: aw = 0.5*m* (q+ z2+2*x) = 302.88 9) Определяем основные геометрические размеры передачи: делительный диаметр d1 = q*m = 8*16 = 128 мм; диагональный диаметр dw1 = m* (q+2*x) = 16* (8-2.14) = 93.76 мм; диаметр вершин витков da1 = d1+2*m = 128+2*16 = 160 мм; диаметр впадин витков df1 = d1-2.4*m = 128-2.4*16 = 89.6 мм; 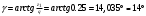 -делительный угол подъема линии витков червяка; -делительный угол подъема линии витков червяка;длина нарезаемой части червяка b1 = (10+5.5*|x|+z1) *m+C = (10+5.5*1.07+2) *16+0 = 286.16 ≈ 287 мм ≈ 290 мм; d2 = dw2 = m* z2 = 16*32 = 512 мм-диаметр вершины зубьев; da2 = d2+2*m* (1+x) = 512+2*16* (1-1.07) = 482.24 мм - делительный диаметр; наибольший диаметр колеса daw2 ≤ da2+ (6*m/ (z1+2)) = 482.24+ (6*16/ (2+2)) = 506.24 мм; диаметр впадин зубьев df2 = d2-2*m* (1.2-x) = 512-2*16* (1.2+1.07) = 439.39 мм; ширина венца z1 = 2, b2 = 0.355*aw= 0.355*302.88 = 107.52 мм ≈ 108 мм; радиусы закрепления зубьев Ra = 0.5*d1-m = 0.5*128-16 = 48 мм; Rf = 0.5* d1+1.2*m = 0.5*128+1.2*16 = 83.2 мм; условный угол обхвата червяка венцом колеса: sinδ = b2 // (da1-0.5*m) =108/ (160-0.5*16) = 0.71=>δ≈45˚; 2 δ = 90˚ в диапозоне 90˚…125˚; 10) Определяем КПД червячной передачи: 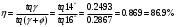 11) Определяем контактные напряжения зубьев колеса 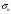 , H/мм2: , H/мм2: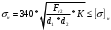 , ,где Fr2 = 2*T2*103/ d2 = 2*2192.8*103/512 = 8565.62 H, окружная сила на колесе; K = 1, так как V2<3 м/с; Vs = (Uф*W2*d1) / (2*cos γ*103) = 2.22 м/с; Тогда σH = 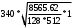 = 122.89 Н/мм2 < [σ] H = 133 H/мм2,где V2 = W2*d2/2000 = 2.105*512/2000 =0.53 м/с; = 122.89 Н/мм2 < [σ] H = 133 H/мм2,где V2 = W2*d2/2000 = 2.105*512/2000 =0.53 м/с;12) Определяем напряжения изгиба зубьев колеса σF, Н/мм2: σF = 0.7*YF2* (Fr2/b2*m) *K ≤ [σ] F, где zv2 = z2/cos3 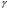 = 32/0.9703=35=> YF2=1.64; = 32/0.9703=35=> YF2=1.64;Тогда σF= (0.7*1.64*8565.62*1) / (16*108) =5.69 H/мм2<< [σ] F=26.625 H/мм2 Верно, вследствие того, что нагрузочная способность червячных передач ограничивается контактной прочностью зубьев червячного колеса. Таблица 6.1 Параметры червячной передачи, мм
Таблица 6.2 Проверочный расчет
1.7 Расчет открытой конической зубчатой передачи 1) Определяем внешний делительный диаметр колеса de2, мм: de2 ≥ 165*, где T2 = 2127.4 H*м; U = 4.49; 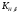 = 1; = 1; 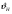 = 1; = 1;2) Определяем углы делительных конусов шестерни δ1 и колеса δ2: δ2 = arctgU = arctg4.49 = 77.44417˚ δ1 = 90 - δ2 = 90-77.44417 = 15.55583˚ 3) Определяем внешнее конусное расстояние Re, мм: Re = de2/ (2*sin δ2) = 629.838/ (2*0.97608) = 322.63646 4) Определяем ширину зубчатого венца шестерни и колеса b, мм: b= ΨR *Re=0.285*322.63646=91.95139≈95 5) Определяем внешний окружной модуль me - для колес с прямыми зубьями, мм: me = 14* T2*1000/ ( 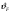 * de2* [σF]) * * de2* [σF]) * 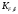 = 14*2127.4*1000/ (0.85*629.838*170.72*95) = 3.43, = 14*2127.4*1000/ (0.85*629.838*170.72*95) = 3.43,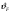 =0.85, =0.85, 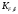 =1; =1;6) Определяем число зубьев колеса Z2 и шестерни Z1: Z2 = de2/ me = 184 Z1 = Z2/U = 184/4.49 = 41 7) Определяем фактическое передаточное число и проверяем его отклонение ΔU от заданного U: UФ = Z2/ Z1 = 184/41 = 4.487 ΔUФ =| UФ - U|/U*100% = |4.487-4.49|/4.49*100% = 0.048%<4% 8) Определяем действительные углы делительных конусов шестерни δ1 и колеса δ2: δ2 = arctgUф = arctg4.487 = 77.43604˚ δ1 = 90 - δ2 = 90-77.43604 = 12.56396˚ 9) Выбираем коэффициент смещения инструмента для прямозубой шестерни Xe1 и коэффициент смещения колес Xe2: Xe1 = 0.26 Xe2 = - Xe1=-0.26 10) Определяем фактические внешние диаметры шестерни и колеса, мм: Диаметр делительный: de1 = me* Z1 = 140.63 de2 = me* Z2 = 631.12 Диаметр вершин зубьев: dae1 = de1+2* (1+ Xe1) * me*cos δ1 = 149.066 dae2 = de2+2* (1 - Xe2) * me*cos δ2 = 633 Диаметр впадин зубьев: dfe1 = de1 - 2* (1.2 - Xe1) * me* cos δ1 = 134.337 dfe2 = de1-2* (1.2+ Xe1) * me* cos δ2 = 629.72 11). Определяем средний делительный диаметр шестерни d1 и колеса, мм: d1 ≈ 0.857* de1≈120.51 d2 ≈ 0.857* de2≈540.869 12) Проверяем пригодность заготовок колес, мм: Dзаг ≤ Dпред Sзаг ≤ Sпред Dзаг = dae+6 мм = 154.066 Sзаг= 8* me=8*3.43 = 27.44 < 200 13) Проверяем контактные напряжения 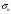 , Н/мм2 , Н/мм2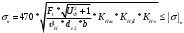 , ,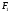 = 2* T2*1000/ (d2) = 2*2127.4*1000/540.869 = 7866.59 Н; = 2* T2*1000/ (d2) = 2*2127.4*1000/540.869 = 7866.59 Н;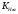 =1; =1; 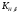 =1; =1; 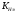 =1.05; =1.05;V=W2*d2/2000=2.105*540.869/2000=0.569 м/с; Cтепень точности - 9; Тогда 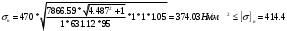 недогрузка - 9.7418%; 14) Проверяем напряжения изгибов зубьев шестерни σF1 и колеса σF2, Н/мм2: σF2 = YF2*Yβ*F1* 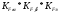 / ( / (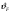 *b* me) ≤ [σ] F2 *b* me) ≤ [σ] F2σF1 = σF2* YF1/ YF2 ≤ [σ] F, где YF2 = 3.63, Z  = Z2/ cos δ2 = 184/0.21752 = 845.89; YF1 = 3.53, Z = Z2/ cos δ2 = 184/0.21752 = 845.89; YF1 = 3.53, Z  = Z1/ cos δ1 = 41/0.97605 = 42; = Z1/ cos δ1 = 41/0.97605 = 42;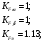 Yβ = 1; Yβ = 1;Тогда σF2 = 3.63*1*7866.59* 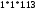 / (0.85*95*3.43) = 116.5024 ≤ [σ] F2 = 170.72 / (0.85*95*3.43) = 116.5024 ≤ [σ] F2 = 170.7231.7582% - нагрузочная способность зубчатой передачи ограничивается контактной прочностью; σF1 = 116.5024* 3.53/ 3.63 = 113.29296 ≤ [σ] F1 = 149.0925 24.013% - нагрузочная способность зубчатой передачи ограничивается контактной прочностью; Таблица 7.1 Параметры зубчатой конической передачи
Таблица 7.2 Проверочный расчет
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||