Да. Зачет №3. Призма
 Скачать 49.5 Kb. Скачать 49.5 Kb.
|
|
Сформулируйте определение призмы. Сделайте чертеж, подпишите элементы призмы. Призма – многогранник с двумя параллельными и равными гранями (многоугольниками), а другие грани при этом являются параллелограммами. Сформулируйте теорему о боковой поверхности прямой призмы. Запишите формулу. Площадь боковой поверхности прямой призмы равна произведению периметра её основания на высоту призмы. S(бок)=P(осн)*H Сформулируйте определение правильной призмы. Правильная призма –это призма, в которой основы являются правильными многоугольниками. Правильная призма может быть, как прямой, так и наклонной. Запишите формулу полной поверхности прямой призмы. Sп = Sб + 2Sосн Сформулируйте определение пирамиды. Сделайте чертеж, подпишите элементы пирамиды. Пирамида — многогранник , в основании которого лежит многоугольник, а остальные грани являются треугольниками , которые имеют общую вершину. Сформулируйте теорему о боковой поверхности правильной пирамиды. Запишите формулу. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему. 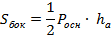 Сформулируйте определение апофемы.. Сделайте чертеж. Апофема — длина перпендикуляра, опущенного из центра правильного многоугольника на одну из его сторон; апофема равна радиусу вписанного в данный многоугольник круга . 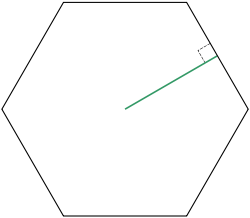 Сформулируйте свойства правильной пирамиды. Пирамида называется правильной, если: ее основание – правильный многоугольник; отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой. Сформулируйте определение усеченной пирамиды. Сделайте чертеж Усеченная пирамида – часть пирамиды, заключенная между её основанием, боковыми гранями и сечением этойпирамиды плоскостью, параллельной основанию. 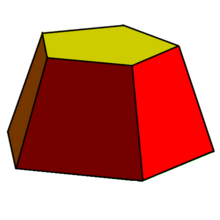 Запишите формулу полной поверхности прямой призмы. Sп = Sб + 2Sосн. |
