контрольная работа 6 кл. Признак перпендикулярности плоскостей
 Скачать 193.87 Kb. Скачать 193.87 Kb.
|
ПЛАН-КОНСПЕКТурока геометрии в 10 классе по теме: «Признак перпендикулярности плоскостей» (2 часа) УМК: «Геометрия 10-11» Автор: Атанасян Л.С. Тема урока: «Признак перпендикулярности плоскостей» Место и роль урока в изучаемой теме: изучается в рамках раздела «Перпендикулярность прямых и плоскостей» Тип урока: урок «открытия» новых знаний
Оборудование: мультимедийное оборудование, презентационный материал, раздаточный материал. Литература: Геометрия. 10-11 классы: учебник для 10-11 кл. общеобразоват. учреждений: базовый и профильный уровни. Атанасян Л. С. Геометрия. 10 класс. Дидактическое пособие. Зив Б.Г. План урока: 1) организационный момент (1 мин.) 2) актуализация знаний (2 мин.) 3) проверка домашнего задания (10 мин.) 4) проведение самостоятельной работы (15 мин.) 5) постановка учебной задачи (1 мин.) 6) «Открытие» нового знания (10 мин.) 7) первичная проверка понимания (1 мин.) 8) первичное закрепление (2 мин.) 9) решение задач (30 мин.) 10) информация о домашнем задании, инструктаж по его выполнению (1 мин.) 11) подведение итогов урока, рефлексия (5 мин.) Ход урока 1. Организационный момент. Включает в себя приветствие учителем класса, подготовку помещения к уроку, проверку отсутствующих. 2. Актуализация опорных знаний. Учитель: Точка А лежит на ребре двугранного угла. Верно ли, что ∠ABC - линейный угол двугранного угла, если лучи АВ и АС перпендикулярны его ребру? Ученики: Нет. Учитель: Верно ли, что ∠BAC - линейный угол двугранного угла, если лучи АВ и АС лежат в гранях двугранного угла? Ученики: Нет. Учитель: Верно ли, что ∠BAC - линейный угол двугранного угла, если лучи АВ и АС перпендикулярны его ребру, а точки В и С лежат на гранях угла? Ученики: Да. Учитель: Линейный угол двугранного угла равен 80°. Найдется ли в одной из граней угла прямая, перпендикулярная другой грани? Ученики: Нет. Учитель: ∠ABC -линейный угол двугранного угла с ребром а. Перпендикулярна ли прямая а плоскости ABC? Ученики: Да. Учитель: Что называется двугранным углом? Ученики: Двугранным углом называется фигура, образованная прямой и двумя полуплоскостями с общей границей, не принадлежащими одной плоскости. 3. Проверка домашнего задания. На дом задано решение задач из учебника под номерами 171, 173, 176, 212. 4. Проведение самостоятельной работы. В ходе урока проводилась самостоятельная работа по теме «Двугранный угол». Она состоит из 5 заданий разного уровня сложности. Сразу после сдачи работ проводится проверка выполнения самостоятельной работы учащимися. Построить линейный угол двугранного угла ВАСК. Треугольник АВС – прямоугольный. Построить линейный угол двугранного угла ВАСК. Треугольник АВС – тупоугольный. Построить линейный угол двугранного угла ВАСК. Треугольник АВС – остроугольный. В тетраэдре DАВС построить линейный угол двугранного угла между плоскостями (DBC) и (ABC), если AD=DB и AC=CB. В параллелепипеде ABCDPQRS построить линейный угол двугранного угла между плоскостями (ABC) и (AQR). 5. Постановка учебной задачи. Учитель: Как мы уже знаем, можно определить перпендикулярность плоскостей по измерению линейной меры двугранного угла, образованного двумя пересекающимися плоскостями. Какие же еще методы существуют? Ученики: определить перпендикулярность плоскостей можно по признаку. Учитель: Итак, тема сегодняшнего урока – признак перпендикулярности плоскостей. 6. Изучение нового материала. Учитель: Открывайте тетради, записывайте сегодняшнее число и тему урока. Запись на доске и в тетрадях: Признак перпендикулярности плоскостей. Учитель: При пересечении двух плоскостей образуются четыре двугранных угла. Углом между пересекающимися плоскостями называется линейный угол φ этого двугранного угла, который 0° < φ ≤ 90° (рис. 1). 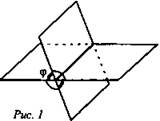 Учитель: Если φ = 90°, то плоскости называются перпендикулярными (взаимно перпендикулярными) (рис. 2). 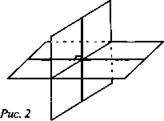 Учитель: Приведите примеры взаимно перпендикулярных плоскостей. Ученики: Плоскости стены и пола, стены и потолка комнаты. Учитель: Ясно, что в этих случаях каждый из четырех двугранных углов, образованных пересекающимися плоскостями, прямой (рис. 2). Рассмотрим признак перпендикулярности двух плоскостей. Теорема: Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны. Дано: α, β, АВ лежит в плоскости α, АВ ⊥ β, АВ ∩ α = А (рис. 3). Доказать: α ⊥ β. 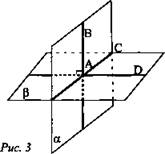 Доказательство: α ∩ β = АС, АВ ⊥ АС, так как АВ ⊥ β по условию. Проведем в плоскости βAD ⊥ AC. ∠BAD - линейный угол двугранного угла. Но ∠BAD =90°, так как ВА ⊥ β. Значит, α⊥ β. Запишите теорему и её доказательство в тетради и сделайте чертёж. 7. Закрепление изученного материала. Учитель: При решении задач используются утверждения: Плоскость, перпендикулярная к ребру двугранного угла, перпендикулярна к его граням (следствие). Перпендикуляр, проведенный из любой точки одной из двух взаимно перпендикулярных плоскостей к линии их пересечения, есть перпендикуляр к другой плоскости (№ 178). Учитель: Решим №172 у доски. Ученик: №172 Дано: ΔАВС, ∠С = 90°, АС лежит в плоскости α, угол между плоскостями α и ABCравен 60°, АС = 5 см, АВ = 13 см (рис. 4).Найти: расстояние от точки В до плоскости α. 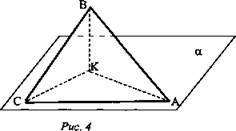 Решение: Построим ВК ⊥ α. Тогда КС - проекция ВС на эту плоскость. ВС ⊥ АС по условию, значит, по теореме о трех перпендикулярах, КС ⊥ АС. Отсюда следует, что ∠ВСК - линейный угол двугранного угла между плоскостью α и плоскостью треугольника, ∠ВСК = 60°. Из ΔВСА по теореме Пифагора: Из ΔВКС: Ответ: 6√3 см. 8. Решение задач. Учитель: из дидактических материалов решим задачу С-12 (1) варианта №3. Ученик: С-12 (1) варианта №3. Два правильных треугольника АВС и BDC расположены так, что их плоскости взаимно перпендикулярны. Найдите тангенс двугранного угла, образованного плоскостями ADC и ABC. Д  ано: ΔАВС и ΔDВС – правильные, (АВС) ⊥ (DВС). ано: ΔАВС и ΔDВС – правильные, (АВС) ⊥ (DВС).Найти: tg(∠(АВС) ⊥ (ADС)). Решение: DH⊥AC, HK⊥AC, следовательно, по ТТП, DK⊥AC.  Где  Ответ: 2. У  читель: из дидактических материалов решим задачу С-11 (1) варианта №3. читель: из дидактических материалов решим задачу С-11 (1) варианта №3.Ученик: С-11 (1) варианта №3. На гранях двугранного угла взяты 2 точки, удаленные от ребра двугранного угла на 6 и 10 см. Известно, что одна из этих точек удалена от второй грани на 7,5 см. Найти расстояние от другой точки до противоположной грани двугранного угла. Дано: А и К лежат на разных гранях двугранного угла с ребром С. ρ(С, А) = 6, ρ(С, К) = 10, ρ(К, β) = 7,5. Найти: ρ(А, α) = ? 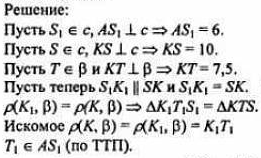 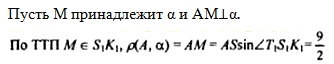 Ответ: 4,5. Учитель: выполним №184 из учебника. Ученик: №184. Общая сторона АВ треугольников АВС и АВD равна 10 см. Плоскости этих треугольников взаимно перпендикулярны. Найти СD, если треугольники: а) равносторонние; б) прямоугольные равнобедренные с гипотенузой АВ. Д 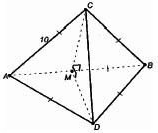 ано: АВ = 10 см, ΔАВС, ΔАВD. ано: АВ = 10 см, ΔАВС, ΔАВD.а) Построим СМ⊥АВ и отрезок МD. В равностороннем ΔАВС: СМ – высота, а значит, и медиана, АМ = МВ = 5 см. В ΔАВD: МD – медиана и высота, то есть МD⊥АВ. ∠СМD – линейный угол внутреннего угла САВD, ∠СМD= 90°. СМ = 10sin60° = 5 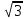 , MD = 5 , MD = 5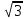 (cм). (cм).СD = 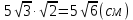 (по теореме Пифагора для ΔСМD). (по теореме Пифагора для ΔСМD).б 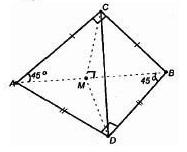 ) Построим СМ⊥АВ. ) Построим СМ⊥АВ.В равностороннем ΔАСВ: СМ – высота, а значит, и медиана. Проводим отрезок DM, DM – медиана в равнобедренном ΔАВD, следовательно, и высота МD⊥АВ. Очевидно, СМ = МА = 5 см, МD = 5 см, СD = 5 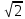 см (по теореме Пифагора для ΔСМD). см (по теореме Пифагора для ΔСМD).Ответ: а) 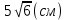 ; б) 5 ; б) 5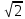 (cм). (cм).9. Домашнее задание. Запись на доске и в дневниках: выполнить вариант домашнего задания на распечатках из пособия Ершовой на листочках – Вариант Б2 самостоятельной работы №16. Выполнить конспект по параграфу 24 «прямоугольный параллелепипед». 10. Подведение итогов. Учитель: Что нового вы узнали сегодня на уроке? Ученики: Узнали, какие плоскости называются перпендикулярными, признак перпендикулярности плоскостей. |
