Математика. Урок №3. Признаки делимости на 3 и на 9
 Скачать 45.82 Kb. Скачать 45.82 Kb.
|
|
Число: 09.09.2022 Урок №3 Тема: признаки делимости на 3 и на 9. Цели: ознакомить учащихся с признаками делимости на 9 и на 3; развивать логическое мышление; воспитывать умение оценивать объективно труд своих товарищей. Информация для учителя Учителю следует обратить внимание учащихся на понятие числа и цифры и формулировку признака делимости («сумма цифр»). Ход урока I. Организационный момент Проверка настроения: прием «Мордашки» (у каждого ученика на столе 3 карточки, нужно показать ту, которая соответствует настроению в данный момент).  В течение урока учитель может несколько раз попросить детей поднять эти карточки. II. Устный счет 1. Упростите: Зх + 4х х + х 4х + 7х — 3х х + х + х + х 10х — х 5х — х 8х — 5х + х 4х + 8х — х + 2 х 2. Назовите 3 числа, меньшие 54, делящиеся на 10. 3. Назовите наименьшее натуральное число. — Назовите наибольшее натуральное число. (Назвать нельзя, так как натуральных чисел бесконечно много.) — Перечислите все цифры, которые мы используем для записи чисел. Современные цифры 1, 2, 3, ..., 9, 0 — ценнейший вклад в сокровищницу математических знаний. Эти цифры позаимствовали арабы в Индии у индусов. 4. На руках 10 пальцев, сколько пальцев на 10-ти руках? (5 · 10 = 50.) 5. Не вычисляя суммы, докажите, что: а) 100 + 250 + 75 делится на 25; б) 36 + 60 + 24 делится на 4; в) 23 + 16 + 44 не делится на 2; г) 18 + 27 + 36 делится на 9; д) 18 + 180 + 11 не делится на 6. — На каких свойствах суммы основаны ваши ответы? (Если каждое слагаемое кратно числу а, то и сумма кратна числу а; если только одно слагаемое суммы не кратно числу а, то и сумма не кратна числу а). III. Индивидуальная работа
IV. Сообщение темы урока — Сегодня мы познакомимся с признаками делимости на 9 и на 3. V. Изучение нового материала 1. Подготовительная работа. — Запишите: Вариант I. 2 трехзначных числа, делящихся на 9. Вариант II. 2 двухзначных числа, делящихся на 9. — Найдите сумму цифр этих чисел. Проверьте, делится ли она на 9. — Запишите четырехзначное число, сумма цифр которого делится на 9. Проверьте, делится ли оно на 9. — Какой вывод можно сделать? (Число, сумма цифр которого делится на 9, делится на 9 и если число делится на 9, то сумма цифр делится на 9.) 2. Работа над новой темой. — У вас у каждого были придуманы свои числа, но результат получился один и тот же. Этот результат, полученный при выполнении данных вычислений, требует обоснований. (Учитель дает пояснения, аналогичные приведенным в учебнике на стр. 13—14 в п. 3.) — Сформулируйте признак делимости на 9. — Попробуйте на примере числа 35 742 обосновать признак делимости на 3. — Сформулируйте признак делимости на 3. 3. Можно записать в тетрадь памятку для учащихся: 1. Число, сумма цифр которого делится на 3, делится на 3. 2. Число, сумма цифр которого делится на 9, делится на 9. — С помощью карточек покажите, понятен ли вам новый материал. VI. Физкультминутка VII. Работа над задачей 1. № 66 стр. 14 (устно). — Прочитайте задачу. — Как вы понимаете задачу? — О чем говорится в задаче? — Обоснуйте свой ответ. (Ответ: а) не может во всех подарках быть 25 конфет, так как число 25 не делится без остатка на 3 и т.д.) 2. № 68 стр. 15 (у доски и в тетрадях). — Прочитайте задачу. — Можно ли сразу ответить на 1 вопрос задачи? (Нет, нужно перевести центнеры в килограммы.) Решение: 1) 2 ц = 200 кг 2) 200 — 60 = 140 (кг) — нужно разложить в 9 ящиков поровну. 3) 140 не делится на 9 без остатка, значит, 60 кг остаться не может. 4) 200 — 56 = 144 (кг) — нужно разложить в 9 ящиков поровну. 5) 144 делится на 9, так как сумма цифр 1+4 + 4 = 9 делится на 9, значит, 56 кг остаться может. (Ответ: а) не может; б) может.) 3. № 80 стр. 16 (с подробным разбором). — Прочитайте задачу. — Какие условия мы должны соблюдать при решении задачи? (Число трехзначное, все цифры нечетны.) — Сколько цифр может стоять на месте сотен в числе? (Любая из 5: 1, 3, 5, 7, 9, мы не можем использовать четные цифры.) — Сколько цифр может стоять на месте десятков? (Любая из 5: 1, 3, 5, 7; 9.) — Сколько цифр может стоять на месте единиц? (Тоже любая из пяти.) Решение: По правилу произведения получаем 5 · 5 · 5 = 125 (чисел) (Ответ: 125 чисел.) VIII. Закрепление изученного материала 1. № 61 стр. 14 (у доски и в тетрадях с подробным комментированием). Рассмотреть 1 число — образец решения показывает учитель, остальные числа - 1 ученик у доски, все в тетрадях. Образец записи: 75 432 7 + 5 + 4 + 3 + 2 = 21 21 : 3 = 7, следовательно, 75 432 делится на 3 21 не делится на 9, следовательно, 75 432 не делится на 9. 2. № 62 стр. 14 (самостоятельно с последующей проверкой). Учителю надо обратить внимание учеников на то, чтобы при записи чисел не использовали только цифры 3 и 9. 3. № 65 стр. 14 (устно). — Ответ подтвердите примерами. (Ответ: нет, например, 13; 43; 53; 83, так как сумма цифр этих чисел не делится на 3 без остатка.) 4. № 74 стр. 15. — Ответ обоснуйте. Запищите примеры, подтверждающие или опровергающие данное утверждение. Записать на доске несколько примеров, которые назвали учащиеся. а) Если каждое слагаемое не кратно числу a, то и сумма не кратна числу а. Это утверждение неверно. Например, 11 и 21 не кратны 4, а их сумма кратна 4, (11 + 21): 4 = 32 : 4 = 8. Мы показали, что сформулированное утверждение неверно, приведя опровергающий его пример. Такой пример называют контрпримером. Приставка «контр» (от латинского contra) означает «против». б) Если уменьшаемое и вычитаемое кратны числу а, то и разность кратна числу а. Данное утверждение верно. Докажем. Если уменьшаемое 72 кратно числу 6 и вычитаемое 48 кратно числу 6, то разность 24 кратна числу 6. Рассмотрим разность 72 — 48 = 12 · 6 — 8 · 6 = (12 — 8) · 6 = 4 · 6 = 24. Аналогично рассмотреть еще несколько примеров, подтверждающих данное утверждение. 5. № 75 стр. 16 (устная работа цепочкой). По очереди учащиеся отвечают, если следующий ученик не согласен с предыдущим ответом, он имеет возможность исправить ошибку. Если возникнут трудности при обосновании ответов, то надо вспомнить таблицу № 38. (Ответ: 1 слагаемое 37 843 и 2 слагаемое 54 321 не делятся на 2, так как эти числа нечетны, но их сумма будет четным числом, следовательно, будет делиться на 2 и т. д.) IX. Самостоятельная работа Взаимопроверка. Вариант I. № 69 (первые две строчки) стр. 15, № 62, № 64 (а) стр. 14. Вариант II. № 69 (вторые две строчки) стр. 15, № 62, № 64 (б) стр. 14. — У кого возникли вопросы по проверке? — Покажите с помощью карточек ваше отношение к процессу проверки. X. Повторение изученного материала 1. Решите устно. 7х = 2; 2х = 7; 8х = 3; 3х = 8. — Как найти неизвестный множитель? (Надо произведение разделить на известный множитель.) 2. № 84 (1, 2) стр. 16 (на доске и в тетрадях). Решение:  (Ответ: n = 127,75; а = 16,5.) № 82 стр. 16 (самостоятельно, устная проверка). Образец решения: (на доске показывает учитель)  (Ответы: 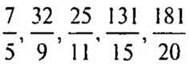 ). ).XI. Подведение итогов урока — Покажите с помощью карточек, какое настроение преобладало у вас на протяжении всего урока. — Какое задание вас заинтересовало больше других? Домашнее задание Учебник стр. 14, выучить правила; № 86, 88 стр. 16; № 90, 91 (а, в) стр. 17. |
