Предмет
|
Алгебра
|
ФИО педагога
|
|
Раздел :Применение производной
|
Дата :
|
|
Класс 10 ЕМН
|
Присутствующие
|
Отсутствующие
|
Тема урока
|
Признаки возрастания и убывания функции
|
Цели обучения по учебной программе
|
10.4.1.26-знать необходимое и достаточное условие возрастания (убывания) функции на интервале;
|
Цели урока
|
Научиться находить промежутки возрастания и убывания
|
ХОД УРОКА
|
Этапы урока
Время
|
Действия педагога
|
Действия ученика
|
Оценивание
|
Ресурсы
|
Начало урока
|
Орг момент . Проверка готовности к уроку
Актуализация знаний
Проводится фронтальный опрос
Что называется функцией?
Что называется областью определения функции?
Какая функция называется возрастающей на промежутке?
Какая функция называется убывающей на промежутке
Что называется приращением аргумента?
Что называется приращением функции?
Что называется первой производной функции?
Повтор пройденных материалов.
Ф. Обратная связь учителя.
|
Приветствует учителя
Дает ответы на поставленные вопросы
|
ФО
Обратная связь учителя
Коментарии одноклассников
|
http://xn--i1abbnckbmcl9fb.xn--p1ai/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/564728/
|
Середина урока
|
К. Проблемный вопрос. Прогноз погоды в Астане.
-Что объединяет эти два графика?
Классификация учащимися представленных графиков функций (возможно, учащиеся предложат свой вариант классификации).
Г. Изучение нового материала.
Определение монотонных функций с помощью производной. Свойства монотонных функций. Свойства графиков монотонных функций.
Учащиеся разбиваются на четыре группы.
Задание для микро группам:
Доказать самостоятельно в группах по определениям возрастающей и убывающей на промежутке функций свойства функций на слайде. Каждая группа представляет свое доказательство. По алгоритму решает первый пример.
Критерий оценивания:
-приводит доказательство теоремы.
-анализирует свои выводы.
-придерживается алгоритму.
-решает задачу.
Если f/(x) > 0 на некотором интервале, то функция возрастает на этом интервале.
Если f/(x) < 0 на некотором интервале, то функция убывает на этом интервале
Следует отметить, что:
Если функция возрастает (убывает) на нескольких промежутках, то следует их перечислить, а не записывать, используя знак объединения промежутков. В последнем случае может нарушаться определение монотонной функции (можно показать на примере обратной пропорциональности).
График функции может «расти» (убывать) выпуклостью вверх или вниз.
Алгоритм:
Указать область определения функции.
2. Найти производную функции.
3. Определить промежутки, в которых
f/(x) > 0 и f/(x) < 0.
4. Сделать выводы о монотонности
функции.
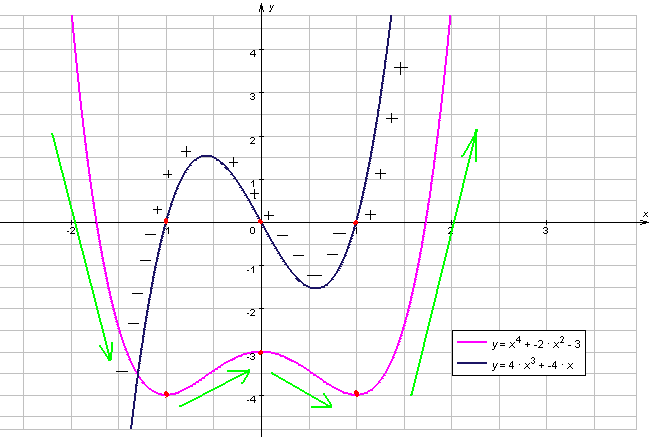
Образец решения по алгоритму:

f(х) = х4 - 2х2 ,
1. D(f) = R
2. f/(x) = 4х3 - 4х,
3. f/(x)>0, если 4х3 - 4х >0, х3 - х >0, х(х-1)(х+1)>0
4. Функция убывает на промежутках (-∞;-1)] и [(0; 1)] .
Функция возрастает на промежутках [(-1; 0)] и [(1; + ∞)]
Наблюдение.
Ф. Взаимопроверка. Учащиеся презентуют свои работы.
К. Первичное закрепление знаний.
Решение онлайн-задач по сайту http://bilimland.kz/ru/#lesson=11460
http://bilimland.kz/ru/#lesson=11811
онлайн-оценивание
Ф.Взаимооценивание.
Анализ и оценка итогов урока.
Учащимся раздать критерий оценивания по уроку.
Учащиеся могут оценить себя по критериям.
|
Работают в группе
По окончанию работы, спикер демонстрирует решение заданий
|
ФО
"Большой палец"
Обратная связь учителя
Коментарии учеников
|
Слайд3
|
http://bilimland.kz/ru/#lesson=11460
http://bilimland.kz/ru/#lesson=11811
|
Конец урока
|
Рефлексия. Учащимся предлагается письменно заполнить таблицу из трех граф. В графу «П» - «плюс» записывается все, что понравилось на уроке, информация и формы работы, которые вызвали положительные эмоции, либо по мнению ученика могут быть ему полезны для достижения каких-то целей. В графу «М» - «минус» записывается все, что не понравилось на уроке, показалось скучным, вызвало неприязнь, осталось непонятным, или информация, которая, по мнению ученика, оказалась для него не нужной, бесполезной с точки зрения решения жизненных ситуаций. В графу «И» - «интересно» учащиеся вписывают все любопытные факты, о которых узнали на уроке и что бы еще хотелось узнать по данной проблеме, вопросы к учителю.
|
|
|
таблица
|
 Скачать 59.02 Kb.
Скачать 59.02 Kb.