курсовая работа. сопротивление материалов ответы. Прочность
 Скачать 0.77 Mb.
|
|
Прочность, жесткость, устойчивость. Прочность– это способность элементов конструкции сопротивляться действию приложен-ных к ним сил без разрушения.  Жесткость – способность элементов конструкции сопротивляться изменению размеров и формы под действием внешних сил в пределах заданных (обычно весьма малых) величин, допусти-мых при условии нормальной эксплуатации. Устойчивость – это способность элементов конструкции под действием внешних сил сохра-нять свою первоначальную форму равновесия. Реальный объект и его расчетная схема. Исследование вопроса о прочности реального объекта начинается с выбора расчётной схемы путём отбрасывания тех факторов, которые не могут заметным образом повлиять на его работоспо-собность в целом. Это совершенно необходимо, так как решение с полным учётом всех свойств реального объекта является принципиально невозможным в силу их бесчисленного множества. Реальный объект, освобожденный от несущественных особенностей, называется расчетной схемой, выбор которой начинается со схематизации свойств материалов на основе гипотез о твердом деформируемом теле. Основные гипотезы о твердом деформируемом теле: 1. Общепринятым считается рассматривать все материалы как однороднуюсплошнуюсреду, независимо от особенностей их микроструктуры. Эта гипотеза позволяет использовать математи-ческий аппарат бесконечно малых величин. Под однородностью материала понимается независимость его свойств от величины выде-ленного объёма. 2. Материал конструкции принимается изотропным, т.е., предполагается, что упругие свойства его одинаковы по всем направлениям. 3. Материал конструкции принимается идеально упругим. Упругость- это свойство тела восстанавливать свои первоначальные размеры частично или полностью после снятия нагрузки. Если тело восстанавливает свои размеры полностью, то оно называется идеально упругим. 4. Гипотеза Сен-Венана:если к некоторой части тела приложена самоуравновешенная система сил (рис.1.1), то эффект действия этих сил (напряжения, деформация) быстро убывает по мере удаления от места их приложения (принцип Сен-Венана). 5. Гипотеза плоских сечений:поперечные сечения бруса плоские и перпендикулярные к оси до нагружения остаются плоскими и перпендикулярными к ней после нагружения. Это допущение называется гипотезой плоских сечений или гипотезой Бернулли 6. Гипотеза неизменности первоначальных размеров. Даже при максимально допустимых нагрузках деформации в конструкциях предполагаются настолько малыми, что можно пренебречь изменениями положения сил в процессе нагружения Силы внешние и внутренние Понятия внутренней и внешней силы применяются к системе тел. Силы, которые действуют между телами, входящими в систему, называются внутренними. Силы, которые действуют со стороны тел, не входящими в систему, называю внешними. Например, для системы молекул газа в замкнутом сосуде, силы притяжения и отталкивания между молекулами – внутренние силы. Сила притяжения молекул к Земле – внешняя сила. Одна и та же сила может быть внутренней или внешней в зависимости от того, какая система тел рассматривается. Метод сечений. Метод сечений заключается в том, что тело мысленно рассекается плоскостью на две части, любая из которых отбрасывается и взамен ее к сечению оставшейся части прикладываются внутренние силы, действовавшие на нее до разреза со стороны отброшенной части. Внутренние силовые факторы. Внутренние силовые факторы. В процессе деформации бруса , под нагрузкой происходит изменение взаимного расположения элементарных частиц тела, в результате чего в нем возникают внутренние силы . По своей природе внутренние силы представляют собой взаимодействие частиц тела, обеспечивающее его целостность и совместность деформаций . Центральное растяжение (сжатие). Растяжение (сжатие) – это такой вид нагружения стержня, при котором в его поперечном сечении возникает внутренняя продольная сила Ν, действующая вдоль центральной оси z. Продольная сила Ν – это равнодействующая всех внутренних нормальных сил в сечении. Для вычисления продольной силы применяется метод сечений. Правило знаков для продольной силы Ν: при растяжении продольная сила положительна, при сжатии отрицательная. Нормальные напряжения в сечении при растяжении (сжатии) вычисляются по формуле 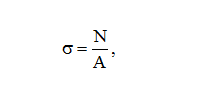 Продольные силы и их определение. Определение продольных сил. Центральное растяжение и сжатие прямого стержня вызывается действием осевых нагрузок. В их состав входят сосредоточенные силы и нагрузки, распределенные по длине всего стержня или его некоторого участка 8 Правило знаков продольных сил Правило знаков продольной силы. Растягивающие продольные усилия принято считать положительными, а сжимающие — отрицательными. При построении эпюры продольных сил положительные значения N обычно откладывают вверх от горизонтальной линии или вправо от вертикальной линии; отрицательные значения N соответственно откладывают в противоположном направлении (либо вниз, либо влево). Абсолютная и относительная продольные деформации. Абсолютная деформация выражает абсолютное изменение какого-либо линейного или углового размера, площади сечения или участка граничной поверхности элемента, выделенного в деформируемом теле, или всего тела. Относительная деформация характеризует относительное изменение тех же величин. Обычно относительную деформацию определяют как отношение абсолютного изменения какого-либо размера к его первоначальному значению. Закон Гука. Закон Гука является основным законом теории упругости, который гласит: сила упругости, возникающая при упругой деформации тела (растяжении или сжатии пружины) пропорциональна удлинению тела (пружины) и направлена в сторону, противоположную направлению перемещений частиц тела при деформации. Если обозначить удлинение тела через x, а силу упругости через Fупр, то закон Гука можно представить в виде формулы: Fупр = - kx, где k – коэффициент пропорциональности, называемый жесткостью тела. Знак минус указывает на то, что силы упругости и удлинения x противоположны. Единицей жесткости в СИ является ньютон на метр (1 Н/м). Сила упругости Fупр (в законе Гука), как и любая другая сила, измеряется в Ньютонах, обозначается как Н. Механические характеристики материалов. Механические характеристики материалов – числовые значения, характери-зующие прочность, жесткость, пластичность, упругость, вязкость и другие свойства. Они определяются экспериментально, на основе результатов испытаний образцов. Допускаемые напряжения. Коэффициент запаса прочности. Допускаемые напряжения. Коэффициент запаса прочности. Механические характеристики материалов позволяют определить величину допускаемых напряжений [σ], входящих в выражения условий прочности. Допускаемое напряжение - это наибольшее напряжение для материала конструкции, при котором в данных условиях нагружения гарантированы необходимая прочность и надежность работы. Понятие о напряженном состоянии в точке. Напряженное состояние в точке – совокупность напряжений, действующих по всевозможным площадкам, проведенным через эту точку. Виды напряженного состояния. В зависимости от величин главных напряжений различают следующие виды напряженного состояния: · линейное, когда только одно главное напряжение отлично от нуля; 14. · плоское, когда два главных напряжения не равны нулю; · объемное, когда все три главных напряжения не равны нулю. Линейное напряженное состояние. Напряженное состояние называется линейным или одноосным, если два главных напряжения равны нулю. Проверка прочности при линейном напряженном состоянии проводится по условию прочности:  Определение нормальных и касательных напряжений при линейном напряженном состоянии. плоском (или линейном) напряженном состоянии удобнее говорить не о направлении осей, а о направлении напряжений (рис. 6): положительное нормальное напряжение вызывает на площадке растяжение, отрицательное – сжатие; положительное касательное. напряжение вызывает поворот площадки по часовой стрелке относительно любой точки на внутренней нормали к площадке, отрицательное – против часовой. Понятие о деформированном состоянии в точке. Деформированное состояние в точке – это совокупность относительных ли-нейных деформаций и углов сдвига для всевозможных направлений осей, проведенных через данную точку. Обобщенный закон Гука.  Основные теории прочности. Первая теория прочности ( Гипотеза наибольших нормальных напряжений ).  Эта теория дает удовлетворительные результаты лишь для некоторых хрупких материалов (бетона, камня, кирпича) и неприменима для пластичных материалов. Вторая теория прочности ( Гипотеза наибольших относительных удлинений ).  Экспериментально эта теория не подтверждается. Третья теория прочности ( Гипотеза наибольших касательных напряжений ) или теория прочности Треска — Сен-Венана. 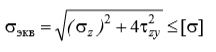 Теория подтверждается для пластичных материалов, одинаково сопротивляющихся растяжению и сжатию. Четвёртая теория прочности ( энергетическая теория прочности ). 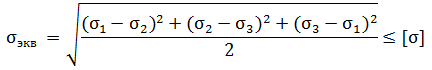 Теория подтверждается для пластичных материалов, одинаково сопротивляющихся растяжению и сжатию. Теория прочности Мора (пятая гипотеза прочности).  Понятие об устойчивости. Усто́йчивость — способность системы сохранять текущее состояние при влиянии внешних воздействий. Если текущее состояние при этом не сохраняется, то такое состояние называется неустойчивым. Определение критической нагрузки шарнирноопорного сжатого стержня (формула Эйлера). Для шарнирно опертого стержня, сжатого по концам, формула Эйлера для определения критической нагрузки:  (коэффициент приведения длины  ).где Е – модуль Юнга;  – минимальный главный центральный момент инерции поперечного сечения стержня (очевидно, что при потере устойчивости изгиб стержня произойдет в плоскости наименьшей изгибной жесткости);  – коэффициент приведения длины, зависящий от формы потери устойчивости; l – длина стержня. Произведение  - приведенная длина стержня.Геометрические характеристики поперечных сечений. Основными геометрическими характеристиками сечений являются пло-щадь, статические моменты плоских сечений, положение центра тяжести, моменты инерции, радиусы инерции и моменты сопротивления. Понятие об изгибе. Изгибом называется вид деформации, при котором искривляется продольная ось бруса. Прямые брусья, работающие на изгиб, называются балками. Прямым изгибом называется изгиб, при котором внешние силы, действующие на балку, лежат в одной плоскости (силовой плоскости), проходящей через продольную ось балки и главную центральную ось инерции поперечного сечения. Изгиб называется чистым, если в любом поперечном сечении балки возникает только один изгибающий момент. Изгиб, при котором в поперечном сечении балки одновременно действуют изгибающий момент и поперечная сила, называется поперечным. Линия пересечения силовой плоскости и плоскости поперечного сечения называется силовой линией. Виды изгиба. При изгибе балки ее продольная ось деформируется: волокна расположенные на выпуклой стороне растягиваются, а на вогнутой стороне - сжимаются. Слой балки, в котором не возникают при изгибе деформации растяжения - сжатия называютнейтральным слоем, а линия пересечения этого слоя с поперечным сечением балки-нейтральной линией (осью). Если силовая плоскость совпадает с одной из главных плоскостей балки, то изгиб называютпрямым илиплоским (рис. 6.1,а). Если силовая плоскость не совпадает ни с одной из главных плоскостей, то такой изгиб называюткосым (рис. 6.1,б). Если в поперечных сечениях балки возникает только внутренний изгибающий момент, то изгиб называют чистым. Если в поперечных сечениях балки возникают внутренние изгибающий момент и поперечная сила, то изгиб называют поперечным. Следует отметить, что как чистый, так и поперечный изгибы могут быть прямыми и косыми. Правило Верещагина. А.К. Верещагин в 1925г. предложил более простой способ решения (формулы) интеграла Мора. Он предложил вместо интегрирования двух функций перемножать эпюры: умножать площадь одной эпюры на ординату второй эпюры под центром тяжести первой. Этим способом можно пользоваться, когда одна из эпюр прямолинейна, вторая может быть любой. Кроме того, ордината берется прямолинейной эпюры. Когда эпюры обе прямолинейны, то тут совсем не важно, чью брать площадь, а чью ординату. Таким образом, эпюры по Верещагину перемножаются по следующей формуле: V=MF⋅M¯¯¯¯¯=ωC⋅M¯¯¯¯¯C Статически неопределимые конструкции. В сопромате статически неопределимыми называются конструкции, в элементах которых усилия не могут быть определены из уравнений статики. Кроме уравнений статики при решении статически неопределимых задач необходимо использовать также уравнения, учитывающие деформации элементов конструкций. Все статически неопределимые конструкции имеют так называемые лишние связи в виде закреплений, стержней или других элементов. Лишними» такие связи называются потому, что они не являются необходимыми для обеспечения равновесия конструкции и ее геометрической неизменяемости, а обусловливаются требованиями к прочности н жесткости конструкции. Число лишних неизвестных, или степень статической неопределимости системы, устанавливается разностью между числом неизвестных, подлежащих определению, и числом уравнений статики. При одной лишней неизвестной система называется один раз или однажды статически неопределимой, при двух - дважды статически неопределимой и т. д. Определение внутренних усилий в статически неопределимых системах при воздействии внешней нагрузки. Понятие о кручении. Основные понятия о кручении. Кручение круглого бруса. Кручением называют такой вид деформации, при котором в любом поперечном сечении бруса возникает только крутящий момент, т. е. силовой фактор, вызывающий круговое перемещение сечения относительно оси, перпендикулярной этому сечению, либо препятствующий такому перемещению. Крутящий момент и его определение. Крутящий момент – это сила, которая умножена на плечо ее приложения, которую может предоставить мотор машине для преодоления тех или иных сопротивлений движению. M = P х 9550 / N. Косой изгиб. Косым изгибом называется разновидность сложного сопротивления, при которой плоскость действия результирующего изгибающего момента не совпадает ни с одной из плоскостей симметрии поперечного сечения Определение положения нейтральной оси и напряжений при косом изгибе бруса. При прямом изгибе нейтральная ось проходит через центр тяжести поперечного сечения бруса и перпендикулярна плоскости изгибающего момента. При косом изгибе нормальные напряжения в центре тяжести поперечного сечения равны нулю, в чем легко убедиться, подставив в формулу (4.9) значения (т. е. координаты центра тяжести). Внецентренное растяжение (сжатие). При внецентренном растяжении - знак “ +” , при сжатии – знак “–“. Таким образом, внецентренное растяжение или сжатие есть частный случай совместного действия изгиба с растяжением или сжатием, причем усилия во всех поперечных сечениях будут одинаковы и все сечения - равноопасные. 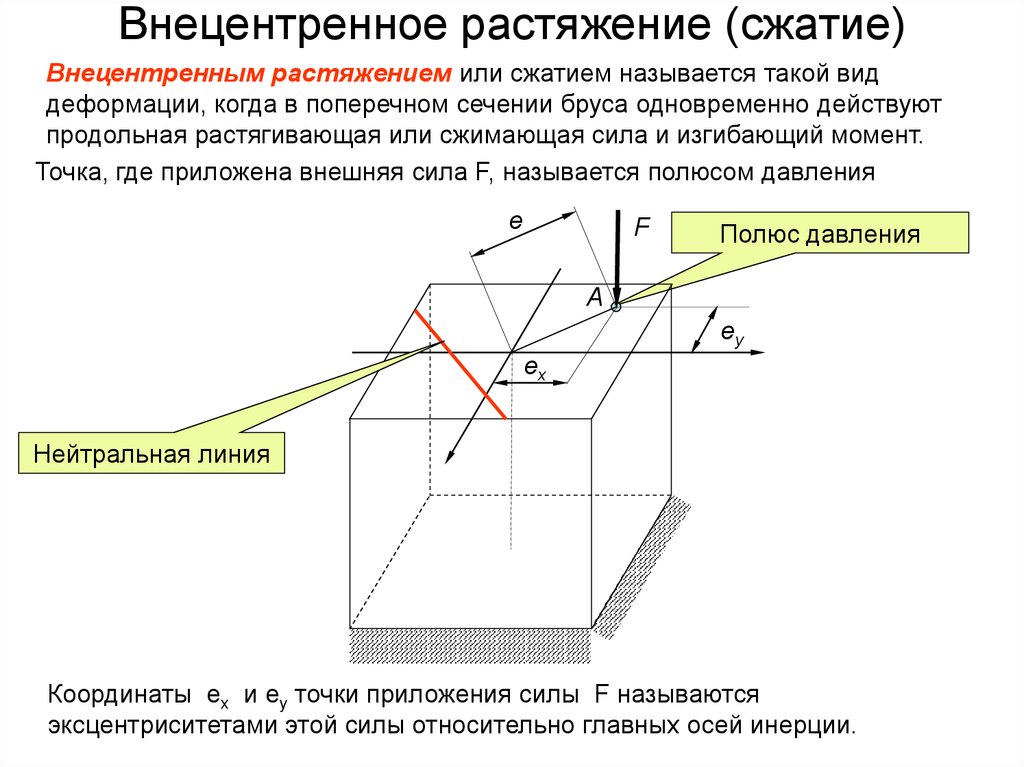 Определение положения нейтральной оси и напряжений при внецентренном растяжении (сжатии). 34 Опоры и опорные реакции. Реакция опоры – это та сила, которая возникает в опоре от действия внешней нагрузки. В зависимости от конструкции опоры и ее назначения, в ней может появляться разное количество реакций, это может быть как сила, так и момент. Шарнирно подвижная опора Шарнирно неподвижная опора Жесткая заделка 35Внутренние силовые факторы при изгибе. 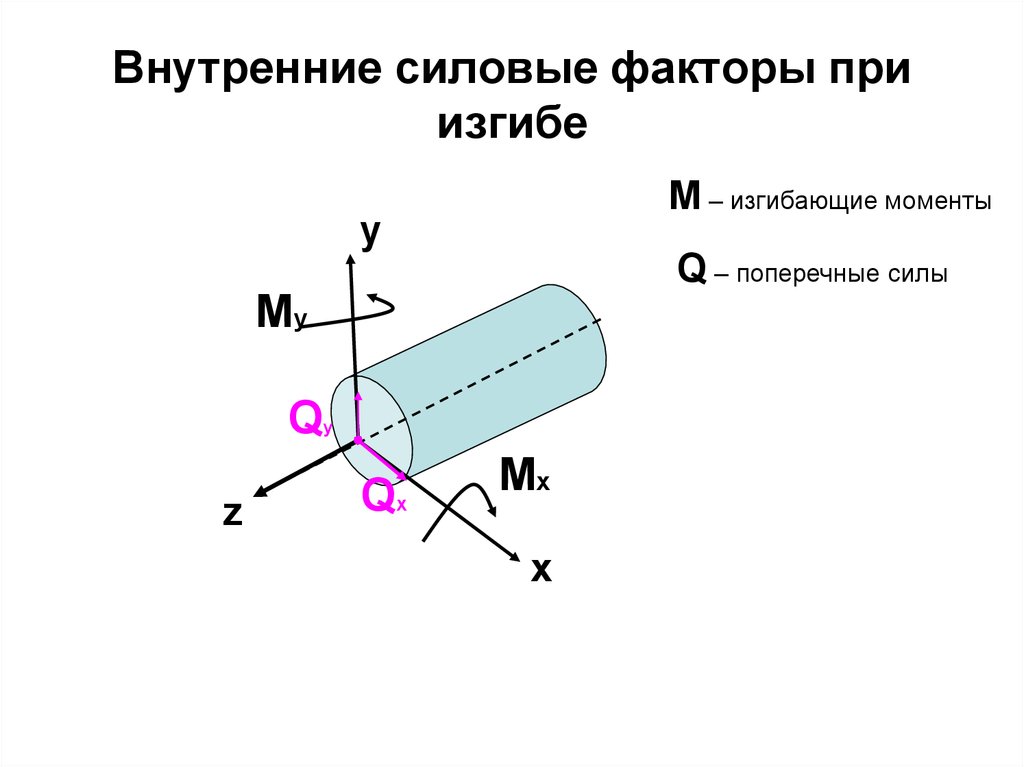 Правило знаков поперечных сил и изгибающих моментов. 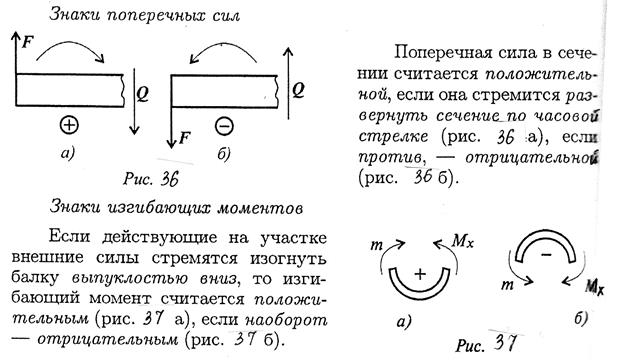 Зависимость между моментами инерции при повороте осей.  Условия прочности и жесткости при кручении. Условие прочности при кручении с учетом принятых обозначений формулируется следующим образом: максимальные касательные напряжения, возникающие в опасном сечении вала, не должны превышать допускаемых напряжений и записывается в виде τ = Mкmax/Wр ≤ [τк], где - берется либо на основании опытных данных, либо (при отсутствии нужных опытных характеристик) по теориям прочности, соответствующим материалу; Mкmax - максимальный крутящий момент в сечении вала; Wр - полярный момент сопротивления. Момент инерции поперечных сечений: статический, осевой, центробежный, полярный. Главные центральные оси инерции. Осевой момент инерции фигуры - этоинтеграл произведений элементарных площадей на квадраты их расстояний до рассматриваемой оси. Формулы осевого момента инерции произвольной фигуры (см. рис. 4.1) относительно осей x и y:  Полярный момент инерции фигуры относительно данной точки (полюса) - это интеграл произведений элементарных площадей на квадраты их расстояний до полюса:  Если через полюс проведена система взаимно перпендикулярных осей x и y, то  , и формула полярного момента инерции равна сумме осевых моментов инерции относительно осей x и y: Из формул осевых и полярного моментов инерции видно: значения осевых и полярного моментов инерции всегда положительны, так как координаты  и расстояние  возведены в квадрат.Центробежный момент инерции фигуры - этоинтеграл произведений элементарных площадей на их расстояния до осей x и y:  Моменты инерции измеряются в единицах длины в четвертой степени (как правило, см4). Понятие момента инерции поперечного сечения ввел в 1834 г. французский ученый Н. Перси. Момент сопротивления поперечного сечения.  Плоское напряженное состояние. Плоское напряженное состояние (ПНС) имеет место при деформации тонкой пластины (пластина считается тонкой, если ее толщина намного, на несколько порядков, меньше двух других ее размеров) силами, приложенными в ее срединной плоскости или равномерно распределенными по ее толщине Определение нормальных и касательных напряжений при плоском напряженном состоянии. Напряженное состояние называется плоским, если одно из главных напряжений равно нулю. Определим нормальные и касательные напряжения в наклонном сечении (см. рис. 1.9). Их можно представить как сумму нормальных и касательных напряжений, возникающих отдельно от 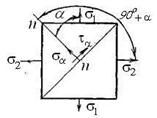 и  . ,где  и  — нормальные напряжения в наклонной площадке, возникающие соответственно от и . Рисунок 1.9 Значение можно определить по формуле (1.1), так как угол между напряжением и нормалью n-n составляет  , а — по формуле (1.3), так как угол  , но в формулу вместо нужно подставить : (1.5)Аналогично для касательных напряжений:  Определение максимальных касательных напряжений и угла закручивания при кручении бруса круглого сечения. Максимального значения касательные напряжения достигают в сечениях волокон, наиболее удаленных от оси закручивания бруса, т. е. на внешней поверхности бруса: если r = R, то τ = τmax. Дифференциальные зависимости между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом. Между изгибающим моментом, поперечной силой и интенсивностью распределённой нагрузки существуют дифференциальные зависимости, основанные на теореме Журавского, которая формулируется следующим образом: поперечная сила равна первой производной от изгибающего момента по абсциссе сечения балки Определение нормальных напряжений при чистом изгибе. Для определения нормальных напряжений необходимо знать положение нейтрального слоя, то есть ρ. Для этого рассмотрим условия равновесия между нагрузочным моментом, действующим на какое-нибудь симметричное сечение F и внутренними силами σdF, распределенными по этому сечению Поперечный изгиб. Поперечный изгиб – изгиб, при котором в сечениях стержня кроме внутрен-него изгибающего момента возникает и поперечная сила Интеграл Мора Интеграл Мора равен произведению площади эпюры (любого очертания) на ординату прямолинейной эпюры расположенную под центром тяжести эпюры , деленному на жесткость стержня . Интеграл (значение) считается положительным, если обе эпюры изгибающих моментов расположены по одну сторону от оси балки.  Зависимость критической силы от условий закреплений сжатого стержня. Пределы применимости формулы Эйлера при потере устойчивости сжатого стержня. Определение перемещений и углов поворота сечений в балках постоянного сечения способом Верещагина. Существует несколько способов (методов) определения перемещений при изгибе: метод начальных параметров; энергетический метод; метод Мора и способ Верещагина. Графо- аналитический способ Верещагина по сути является частным случаем метода Мора при решении сравнительно простых задач, поэтому его еще называют способом Мора – Верещагина Запишем формулу Верещагина y = (1/EJ)*ωг*М1г, (1.14) где y –перемещение в интересующем сечении; E –модуль упругости; J –осевой момент инерции; Удар. Удар - это происходящее в результате соприкосновения взаимодействие движущихся тел. Удар характеризуется резким изменением скоростей частиц взаимодействующих тел за малый промежуток времени, при этом сила удара достигает очень большого значения. В качестве примера можно привести действие кузнечного молота на кусок металла, удар падающего груза при забивке свай, воздействие колеса вагона на рельс при перекатывании через стык. 51 Основные допущения и понятия теории удара За время совершения удара очень трудно произвести измерения, связанные с определением силы удара. Поэтому обычно производится условный расчет на удар, по которому определяются внутренние силы и перемещения, возникающие в стержне. Сначала определяется наибольшее динамическое перемещение точки стержня, по которой наносится удар, а затем определяется напряженное состояние стержня. Существуют следующие допущения при расчете стержня на удар: Допущение 1: деформация стержня, вызванная ударной нагрузкой, описывается законом Гука, а сам стержень является линейно деформируемой системой. При этом модуль Юнга имеет такое же значение, как и при статическом нагружении стержня; Допущение 2: работа, совершаемая падающим грузом, полностью переходит в потенциальную энергию деформации стержня; Допущение 3: масса стержня, воспринимающего удар, пренебрежимо мала по сравнению с массой падающего груза; Допущение 4: удар считается неупругим. Статически неопределимые стержневые системы. Статически неопределимыми называются системы, для которых внешние реакции и внутренние силовые факторы не могут быть определены только из уравнений равновесия твёрдого тела. В таких системах связей больше, чем необходимо для равновесия Метод сил Метод сил. Суть этого метода заключается в том, что заданная статически неопределимая система освобождается от дополнительных связей как внешних, так и внутренних, а их действие заменяется соответствующими силами и моментами. Канонические уравнения метода сил. Канонические уравнения метода сил отрицают перемещения в основной системе по направлению лишних неизвестных от совместного действия внешней нагрузки и неизвестных сил в отброшенных связях. Этим и отождествляется работа заданной статически неопределимой расчетной схемы балки и ее статически определимой основной системы. Оценка прочности стержней круглого сечения при изгибе с кручением по 3-ей и 4-ой теориям прочности. III теория прочности  В нашем случае  (III)IV теория прочности  В нашем случае  (IV)Формулы (I)-(IV) используются для проверки прочности валов с заданными размерами сечений. I и II теории прочности рекомендуются для валов из хрупких материалов (чугун), для которых  (растяжение). III и IV теории прочности (т.п.) рекомендуется для валов из пластических материалов (стали и т.д.). При наличии в опасном сечении вала  ,  вычисляется с ее учетом (14) |