реферат по теории и исп карт. Проекции морских карт
 Скачать 194.92 Kb. Скачать 194.92 Kb.
|
|
Содержание
Введение Морские навигационные карты являются одним из важнейших пособий для обеспечения безопасного плавания судов. На морские навигационные карты наносят отдельные участки моря с указанием глубин и грунтов, очертания береговой линии и рельефа, навигационные знаки и опасности. Значение морских навигационных карт в судовождении очень велико. Являясь уменьшенным изображением участков земной поверхности на плоскости, морская навигационная карта как бы рассказывает судоводителю о тех районах и условиях, в которых проходит плавание судна. Морская навигационная карта предупреждает моряка об опасностях и одновременно подсказывает, как ему лучше проложить свой курс. Способ условного изображения поверхности Земли на плоскости называют картографической проекцией. Известно, что при плавании судна одним и тем же неизменным курсом его путь на поверхности земного шара изобразится кривой линией, называемой локсодромией («косой бег»), которая пересекает все меридианы под одним углом. Поскольку поверхность Земли имеет форму шара, то ее изображение на плоскости невозможно осуществить без искажений. Значит, не существует такой картографической проекции, которая бы не искажала изображаемую на ней земную поверхность. Из большого числа различных картографических проекций можно, однако, подобрать такую, которая удовлетворяла бы основные требования, предъявляемые к морской карте. Аэронавигационные карты предназначены для навигационной подготовки и навигационного обеспечения полетов самолетов. При решении различных задач навигации возникает необходимость определять географические координаты точек, измерять направления и углы, измерять расстояния между двумя пунктами, разности этих расстояний и т. п. В этой связи при оценке и выборе проекций для аэронавигационных карт, прежде всего, учитывается характер искажений проекции и величины этих искажений; вид сетки меридианов и параллелей, характер изображения линий пути и линий положения. Проекция карты должна обеспечить изображение ортодромии (геодезической линии) практически прямой линией для каждого этапа маршрута. В данном реферате рассмотрены проекции, используемые для морской и аэронавигации. 1 Проекции морских карт Различают морские навигационные карты и аэронавигационные карты. Особенностью морских навигационных карт является использование проекции Меркатора, которая удобна для навигатора тем, что путь корабля, идущего постоянным курсом (по определенному азимуту), изображается на ней прямой линией. Наряду с сеткой меридианов и параллелей на навигационные карты дополнительно наносят специальные координатные сетки для определения положения корабля радионавигационными средствами. Выделяются также объекты, дающие отражение на экранах локаторов. В проекции Меркатора с удалением от главной параллели искажения очень быстро нарастают. Чтобы в пределах выделенного пространства искажения были как можно меньше, для морских навигационных карт, создаваемых в проекции Меркатора, для разных акваторий используются разные официально установленные главные параллели. Широты главных параллелей некоторых крупных водоемов указаны в таблице 1. Таблица 1 – Главные параллели проекции Меркатора для морских карт
В полярных районах проекция Меркатора совершенно неприменима. Как известно, в этой проекции полюса на карте вообще не отображаются. Поэтому в полярных районах ее заменяет равноугольная азимутальная стереографическая проекция. Для решения специальных навигационных задач применялись и другие картографические проекции: гномоническая, двуазимутальная, двуэквидистантная, Литтрова. Азимутальная гномоническая проекцияприменяется благодаря ее замечательному для навигации свойству: как уже отмечалось, в ней ортодромия изображается прямой линией. Если в проекции Меркатора прямой линией изображается локсодромия и проекция удобна для того, чтобы вести корабли по заданному постоянному курсу, то с помощью азимутальной гномонической проекции навигацию можно осуществлять по кратчайшему расстоянию между заданными пунктами. В двуазимутальной проекцииортодромии также изображаются прямыми линиями. Кроме того, не искажаются углы с двух центральных точек на любые другие точки карты. В этих центральных точках устанавливаются радиопеленгаторы. Проекция служит для местоопределения корабля в море. Двуазимутальная проекция может быть получена аффинным преобразованием гномонической проекции путем сжатия ее в направлении, параллельном линии, соединяющей упомянутые две центральные точки. При совмещении двух центральных точек в одну проекция превращается в гномоническую. Проекцию независимо предложили дважды: в Германии в 1914 г. (Н.Маигег, 1868-1945) и в Англии в 1922 г. (Ch.F.Close, 1865-1952). В двуэквидистантной проекциисохраняются ортодромические расстояния по прямым линиям от любой точки до двух центральных точек на карте. Проекция используется для определения местоположения корабля по измеренным расстояниям от корабля до двух заданных центральных точек. В этих точках устанавливаются радиостанции дальномерной радионавигационной системы. Двуэквидистантную проекцию независимо предложили авторы двуазимутальной проекции — в Германии (1919) и в Англии (1921). Проекция Литтрова(J. J. Littrow) разработана в Австрии в 1833 г. В этой проекции центральный меридиан и отстоящий от него на 90° меридиан изображаются прямыми линиями, остальные меридианы — гиперболы. Параллели — эллипсы, кроме экватора, который прямолинеен и является большой осью эллипсов. Таким образом, картографическая сетка представляет собой систему со-фокусных эллипсов и гипербол. Весь земной шар в этой проекции отобразить невозможно. Особенностью проекции является то, что в ней сохраняются углы между прямой линией, параллельной центральному меридиану, и направлением на точку на этом центральном меридиане. В XIX в. проекция использовалась Британским флотом для определения направлений с текущих точек в море на центральный пункт. В настоящее время благодаря внедрению Глобальных навигационных спутниковых систем и сопутствующих электронных навигационных комплексов, обеспечивающих высокоточное определение местоположения корабля и вождение судна по кратчайшему расстоянию или иному произвольной траектории маршруту, все эти проекции теряют практическое значение и постепенно становятся достоянием истории [1]. 2 Проекции аэронавигационных карт 2.1 Назначение аэронавигационных карт. Основные проекции, используемые при их создании Авиационные карты по назначению подразделяются на: полетные (применяемые для самолетовождения по маршруту и районам полетов); бортовые (применяемые для самолетовождения с использованием радиотехнических и астрономических средств); специальные (карты магнитных склонений, часовых поясов, для определения места воздушных судна с помощью гиперболических систем, радиомаяков, радионавигационные и др.); карты для выполнения специальных полетов, связанных с отысканием малых объектов на местности, не обозначенных на полетных картах. Аэронавигационные карты ИКАО, выпускаемые странами, входящими в международную организацию гражданской авиации, включают карты различных типов, которые применяются только в международной гражданской авиации и не распространяются на полеты государственных судов (военных, таможенных, полицейских и т.п.). В их состав, например, входят карты для использования в ходе полета между этапами взлета и посадки: карты районов, маршрутные карты, карты стандартного вылета и прибытия по приборам, карты захода на посадку по приборам и карты визуального захода на посадку. Другая группа таких карт включает карты аэродромных препятствий, карты местности для точного захода на посадку и т.п. Третья группа карт предназначена для использования во время наземного аэродромного движения воздушных судов. В четвертую группу входят карты, предназначенные для визуальной аэронавигации, прокладки линий пути и использования в целях планирования. В эту группу например, входят аэронавигационные карты ИКАО масштабов 1:1000 000, 1:500 000, аэронавигационная карта мелкого масштаба и карта для прокладки курса. Имеется группа карт ИКАО специального назначения, на которых отображаются необходимые сведения для самолетовождения на различных его этапах, главным образом, посадки. Создаются также карты для счисления и прокладки пути (преимущественно по магнитному компасу, угломерным радиотехническим средствам - радиомаяку и радиопеленгатору) и радионавигационные карты, основанные на принципах пеленгации, выполнения измерений дальности и их разностей, т.е. карты с дальномерными или гиперболическими сетками. Таким образом, исходя из назначения аэронавигационных карт и географических особенностей картографируемых территорий, все аэронавигационные карты можно разделить на площадные, полимаршрутные, маршрутные и аэродромные, создаваемые в различных масштабах и картографических проекциях. Для площадных карт используются: проекция Меркатора; проекции Гаусса-Крюгера и UTM; равноугольная коническая проекция; равноугольная азимутальная проекция эллипсоида; гномоническая проекция; видоизмененная простая поликоническая; равнопромежуточная вдоль вертикалов азимутальная проекция; равновеликая азимутальная проекция. Для маршрутных и полимаршрутных карт используются проекция Меркатора и равноугольная коническая проекция в косой ориентировке, обеспечивающие хорошую ортодромичность и локсодромичность в пределах полосы полетов по отдельным маршрутам или совокупности маршрутов. Для аэронавигационных карт подходов и аэродромов часто используются проекции топографических карт и сами эти карты. При создании аэронавигационных карт специального назначения применяются равноугольная коническая проекция, проекция Меркатора, гномоническая проекция и равно-промежуточная вдоль вертикалов азимутальная проекция. Могут быть использованы двуазимутальная и двуэквиди-стантная проекции, а также проекция Литтрова. Отметим, что при определении длин и азимутов по картам, составленным в проекциях Гаусса-Крюгера, UTM, конической и азимутальной проекциях, можно воспользоваться формулами редукции в азимуты и в длины за кривизну изображения геодезических линий и за изменения масштабов длин, приведенные в данного раздела [2]. 2.2 Двуазимутальные проекции Прямоугольные координаты точек проекции определяются в соответствии со следующими заданными условиями: все дуги больших кругов (ортодромии) на проекции изображаются прямыми линиями; углы в двух заданных точках, например, в точках положения радиопеленгаторных станций не искажаются (рис.1). Формулы для вычисления прямоугольных координат текущих точек в данной проекции шара с особыми точками 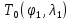 и и 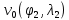 принимают вид принимают вид 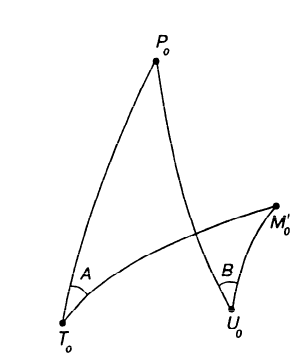 Рисунок 1- Построение двуазимутальной проекции 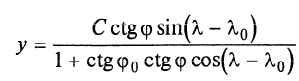 Здесь: 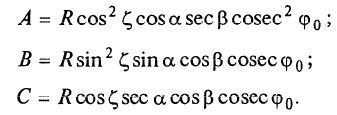 Величины 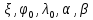 определяются из выражений определяются из выражений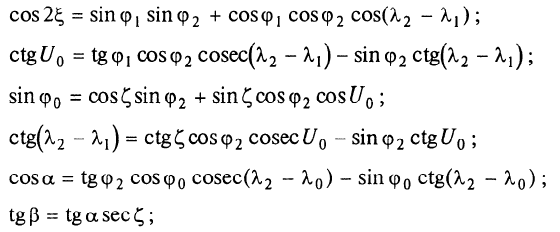 R - радиус Земли, устанавливаемый из условия отсутствия искажений длин в особых точках. Проекция является аффинным преобразованием гномони-ческой проекции. Она может быть использована для прокладки радиопеленгов [2]. 2.3 Эквидистантная по двум особым точкам проекция Прямоугольные координаты точек проекции определяют, исходя из следующего. Пусть на рисунке 2 PA, OA- прямолинейные отрезки, равные ортодромическим расстояниям до данной текущей точки А от двух фиксированных точек Р и О. Первую примем за полюс полярной системы координат, а вторую - за начало прямоугольной системы координат хоу, ось х которой направлена вдоль линии ОР (Г.М.Кирьяков, 1965).  Рисунок 2 – Эквидистантная по двум особым точка проекция Согласно условию имеем 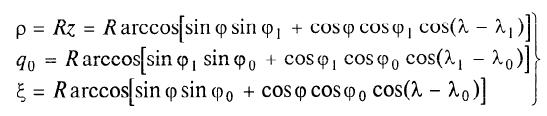 (1) (1)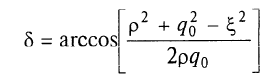 (2) (2)В принятой системе координат прямоугольные координаты проекции определяются по формулам 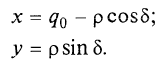 Частные масштабы длин вдоль вертикалов и альмукантаратов нетрудно найти из 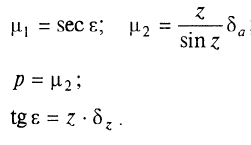 Здесь частные производные 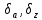 и другие определяются с использованием формул (1), (2), а также выражений и другие определяются с использованием формул (1), (2), а также выражений 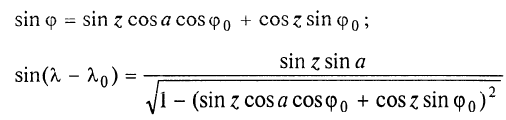 Поскольку получаемые при этом формулы вычисления весьма громоздки, то значения частных масштабов целесообразнее определять численными методами по прямоугольным координатам данной проекции [2]. 2.4 Проекция Литтрова Пусть на рисунке 3 линия 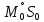 - геометрическое место - геометрическое местоточек, азимуты ортодромии с точек  которых на пункт которых на пункт 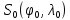 имеют постоянную величину. Такие линии называются изоазимутами. имеют постоянную величину. Такие линии называются изоазимутами.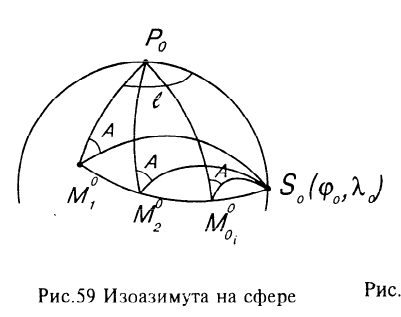 Рисунок 3 – Изоазимута на сфере Для каждой из точек  изоазимуты можно записать по формуле четырех смежных элементов сферического треугольника P0S0M°соотношение изоазимуты можно записать по формуле четырех смежных элементов сферического треугольника P0S0M°соотношение откуда Чтобы изображение изоазимута в некоторой проекции было прямой линией, образующей c осью х некоторый угол α = A, плоские прямоугольные координаты х,у точек М изображения изоазимута в этой проекции должны быть связаны соотношением (рис.4) у = (х0-x)tgα.  Рисунок 4 – Изоазимута на плоскости (в проекции Литтрова) Если положить, что формулы прямоугольных координат проекции имеют вид то приведенные выше уравнения удовлетворяются, прямые SMизображают изоазимуты точек осевого меридиана (l=0, y=0), ось абсцисс - это изображение меридиана λ=λ0=0, ось ординат - это изображение экватора φ = 0. Частные масштабы длин данной равноугольной проекции определяются из выражения 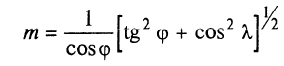 Параллели в проекции - эллипсы, а меридианы - гиперболы. Каждая точка картографической сетки изображает две точки шара 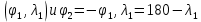 . S - изображение точки пересечения изоазимуты с осью абсцисс. Картографическую сетку проекции Литтрова называют еще сеткой Вейра [2]. . S - изображение точки пересечения изоазимуты с осью абсцисс. Картографическую сетку проекции Литтрова называют еще сеткой Вейра [2].Список литературы 1. Серапинас Б.Б. Математическая картография: Учебник для вузов. - М.: Издательский дом «Академия», 2005 2. Бугаевский Л.М. Математическая картография: Учебник для вузов. – М.: 1998 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
