курсовая работа по дисциплине конструкция ад. Курсовой конструкция. Проект конструкции узла турбины высокого давления
 Скачать 0.92 Mb.
|
|
Схема нагружения диска (см. приложение Д) 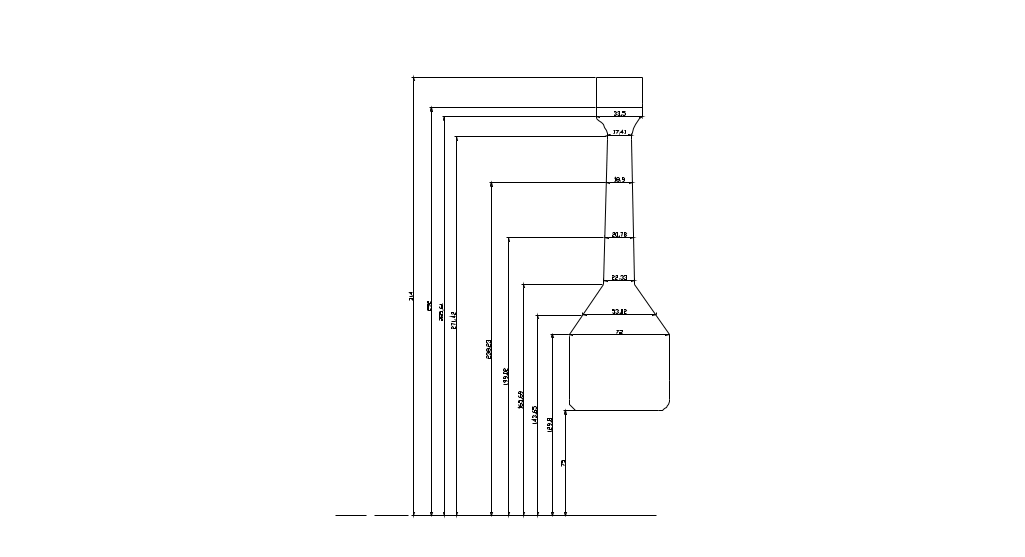 Рис. 17. Схематичное изображение диска 3.4. Определение контурной нагрузки, приложенной к ободу диска. Для определения контурной нагрузки, приложенной к ободу диска необходимо знать массу пера лопатки и массу выступа диска. a) масса пера лопатки  см. 2.7.б) масса выступа диска  где  =33.5 мм -толщина выступов диска,  =8150 кг/м3 - плотность материала,  =314 мм -радиус впадин диска,  =320 мм - радиус корневого сечения лопатки, Z=72 – количество лопаток в диске, Vкарм=0,0000048 м3 3.5. Определение расчётного режима по частоте вращения. В данной работе мы исследуем диск только на одном режиме – максимальном. Прочностные расчёты на меньших режимах можно опустить. Частоту вращения ротора на этом режиме мы берём из задания -  .3.6. Определение зависимости предела длительной прочности материала диска от радиуса. Вычислим предел прочности согласно [5, стр.61]. Для этого рассчитаем уровень нагружения  . Затем 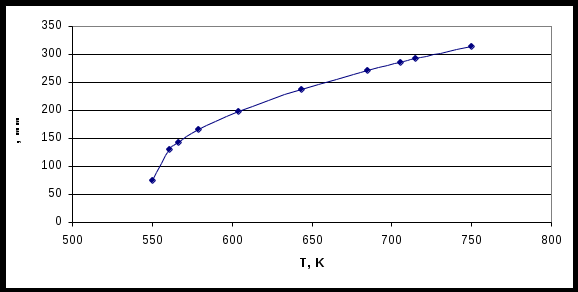из графика [5, стр.61] подставив значения Р найдём значения στ в необходимых сечениях диска. Так как распределение температуры по радиусу диска – прямая (см. п. 3.2.), то мы можем найти температуру по уравнению прямой.Тогда:                                Рис. 18 Изменение температуры по радиусу диска 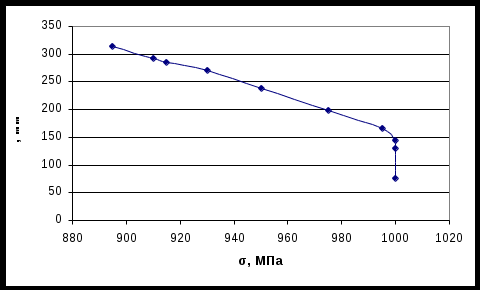 Рис. 19 Изменение σДЛ по радиусу диска 3.7. Расчёт коэффициентов запаса. Для начала введём следующие исходные данные в программу «Strong»:  (см. п. 3.5.) N=10 (см. п. 3.3.) Z=87 (см. п. 2.3.)  (см. п. 2.7.) (см. п. 3.4.)  Табл. 5 Исходные данные.
Результаты расчета:           Теперь построим зависимость К от радиуса диска. 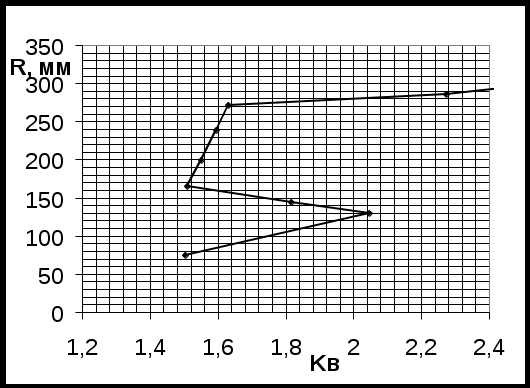 Рис. 20. Распределение коэффициентов запаса по радиусу диска. 3.8. Оценка работоспособности диска по условиям прочности. В п. 3.7. мы получили коэффициенты запаса прочности по 9 сечениям. Согласно рекомендациям [3, стр.24] К не может быть меньше 1,4. Видно, что наш диск удовлетворяет условиям прочности и корректировки его геометрии не требуется. 3.9 Анализ результатов 4. Расчет лопатки на колебания. 4.1 Методика определения низшей собственной частоты колебаний лопатки. Расчетное определение собственных частот колебаний лопатки является пространственной задачи динамической теории упругости. Для ее решения используются методы и модели, различающиеся точностью, возможностью учета тех или иных особенностей конструкции и условий работы лопатки и, разумеется, трудоемкостью. Стержневые модели используют для приближенных расчетов собственных частот изгибных и крутильных колебаний лопаток. Стержневые модели позволяют с достаточно высокой точностью определять несколько низших собственных частот, они непригодны для анализа пластиночных и смешанных форм колебаний, не позволяют учитывать влияние полок. В основе этих моделей лежит допущение о том, что напряженное состояние лопатки одноосное. В случае изгибных колебаний принимается по внимание только нормальное напряжение в направлении оси лопатки; оно считается распределенным по сечению лопатки по линейному закону, нейтральная линия при изгибе совпадает с осью наименьшей жесткости корневого сечения. В случае крутильных колебаний аналогичные допущения принимаются относительно касательного напряжения. Расчет собственных частот по стержневой модели сводится к анализу уравнения в частных производных. В аналитическом виде удается определять собственные частоты и формы колебаний лопаток постоянного поперечного сечения без учета закрутки профиля и изменения температуры по длине и сечению лопатки. Для лопаток переменного по длине сечения наиболее простым и, в то же время, достаточно точным методом определения низшей собственной частоты изгибных колебаний является энергетический метод (метод Рэлея). В его основе лежит идея расчета частоты колебаний по заданной собственной форме; форма колебаний задается априорно, исходя из самых приближенных представлений, а собственная частота рассчитывается с использованием закона сохранения энергии. Рассмотрим применение метода Рэлея для расчета низшей собственной частоты изгибных колебаний невращающейся лопатки. Если пренебречь потерями энергии, в любой момент времени сумма кинетической энергии К и потенциальной энергии П колеблющейся лопатки согласно закону сохранения энергии есть величина постоянная: К+П=const . В 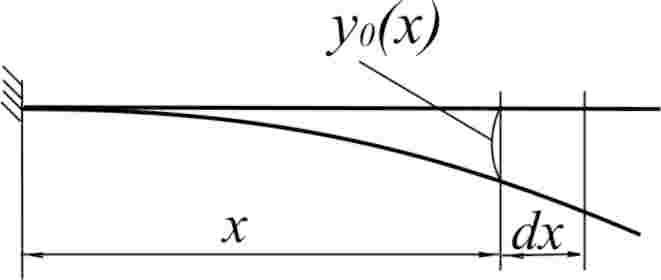 Рис.21. К расчету собственной частоты колебаний невращающейся лопатки положении равновесия потенциальная энергия равна нулю, а кинетическая энергия достигает максимума Кmax. В положении максимального отклонения от равновесия, наоборот, кинетическая энергия равна нулю, а потенциальная - максимальна Пmax. Следовательно Кmax=Пmax. Для определенности будем рассматривать лопатку как консольно закрепленный стержень длиной L (рис.17) с плотностью материала ρ, модулем упругости E, изменяющимися по длине площадью сечения F(x) и моментом инерции I(x). Рассматриваем гармонические колебания с круговой собственной частотой р. Перемещения произвольной точки оси лопатки с координатой x задаем в виде произведения гармонической функции времени на функцию y0(x) , которая представляет собой распределение амплитуд колебаний по координате, то есть форму колебаний:  .Форму колебаний y0(x) будем считать известной. Для элемента лопатки dx(рис.21) максимальная кинетическая энергия равна  Д  ля всей лопатки максимальная кинетическая энергия определяется интегрированием Потенциальная энергия лопатки в момент максимального отклонения от положения равновесия определяется известным из сопротивления материалов соотношением для потенциальной энергии изогнутого стержня: 0  где M(x) – изгибающий момент, соответстыующий прогибу y(x) , который в соответствии с уравнением изогнутой оси стержня равен:  Находим круговую собственную частоту 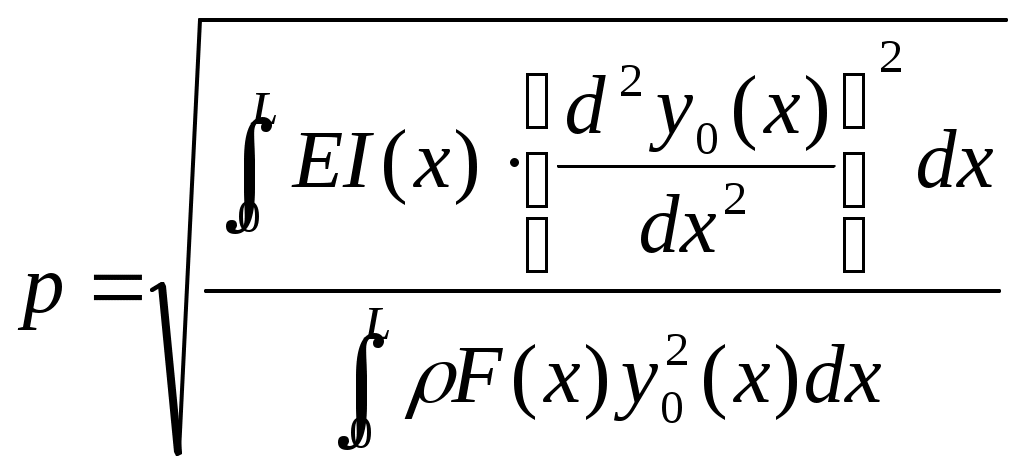 Методом Рэлея может быть получено соотношение для первой собственной частоты крутильных колебаний: 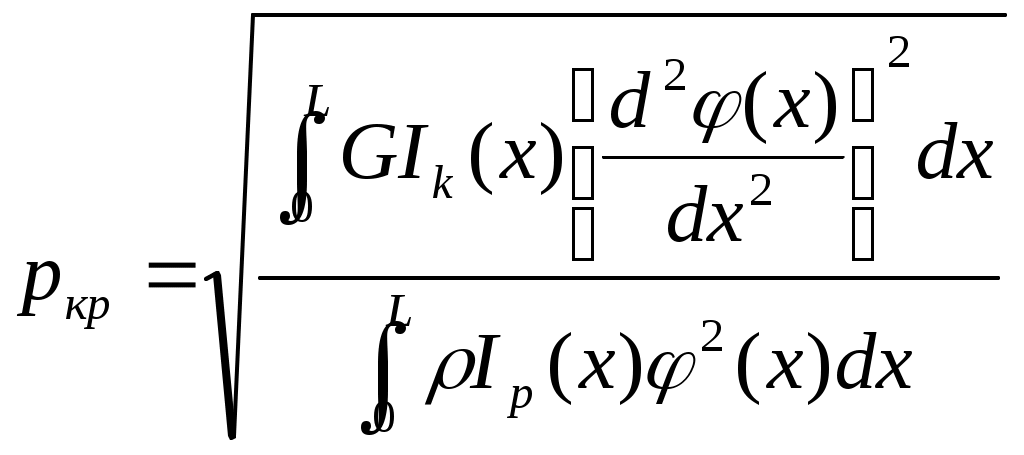 где φ(x) – приближенная форма крутильных колебаний. Форма колебаний в методе Рэлея задается априорно, она лишь должна удовлетворять граничным условиям. Для изгибных колебаний, например, это отсутствие перемещений и поворота сечения в заделке (корневом сечении):  Получающиеся методом Рэлея приближенные значения собственных частот всегда выше точных и тем ближе к ним, чем ближе к действительной заданная приближенно собственная форма. Практика расчетов показывает, что соотношение дает достаточно точные результаты, если форму колебаний принимать совпадающей с функцией прогибов от равномерно распределенной статической нагрузки. При применении метода Рэлея можно с достаточной для практических расчетов точностью получать только частоты колебаний по первой изгибной и первой крутильной формам. Для более высоких собственных частот формы колебаний более сложны, и априорно задать их с достаточной точностью трудно. 4.2 Подготовка исходных данных для определения низшей собственной частоты. Данные используются те же, что в п. 2.7, с той лишь разницей, что вместо параметра R в расчетах используется параметр x – координата сечения в радиальном направлении, считая от корня пера. Табл. 6. Исходные данные.
 |