Курсовая проектирование синхронного генератора. Проектирование синхронного генератора
 Скачать 1.99 Mb. Скачать 1.99 Mb.
|
11 РАСЧЁТ ПРЕВЫШЕНИЯ ТЕМПЕРАТУРЫ ОБМОТКИ СТАТОРА152 Удельный тепловой поток на 1 м2 внутренней поверхности статора 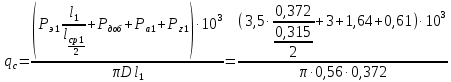 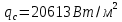 153 Превышение температуры внешней поверхности статора над температурой охлаждающего воздуха 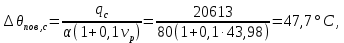 где 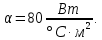 154 Плотность теплового потока с внешней поверхности лобовых частей 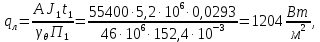 где удельная проводимость меди при 75 ○С 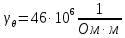 , периметр паза (без учета клина) П1 = 152,410–3 м. , периметр паза (без учета клина) П1 = 152,410–3 м.155 Превышение температуры внешней поверхности лобовых частей обмотки статора над температурой охлаждающего воздуха 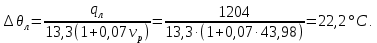 Перепад температуры в пазовой изоляции обмотки статора (см. п. 30). 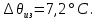 156 Среднее превышение температуры обмотки статора 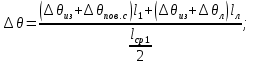 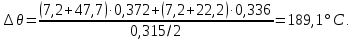 12 ОПРЕДЕЛЕНИЕ ТОКОВ КОРОТКОГО ЗАМЫКАНИЯ157 Ударный ток короткого замыкания 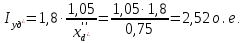 158 Уточненное значение тока короткого замыкания 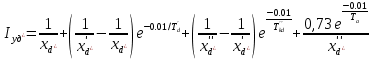 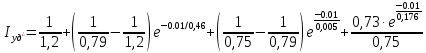 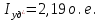 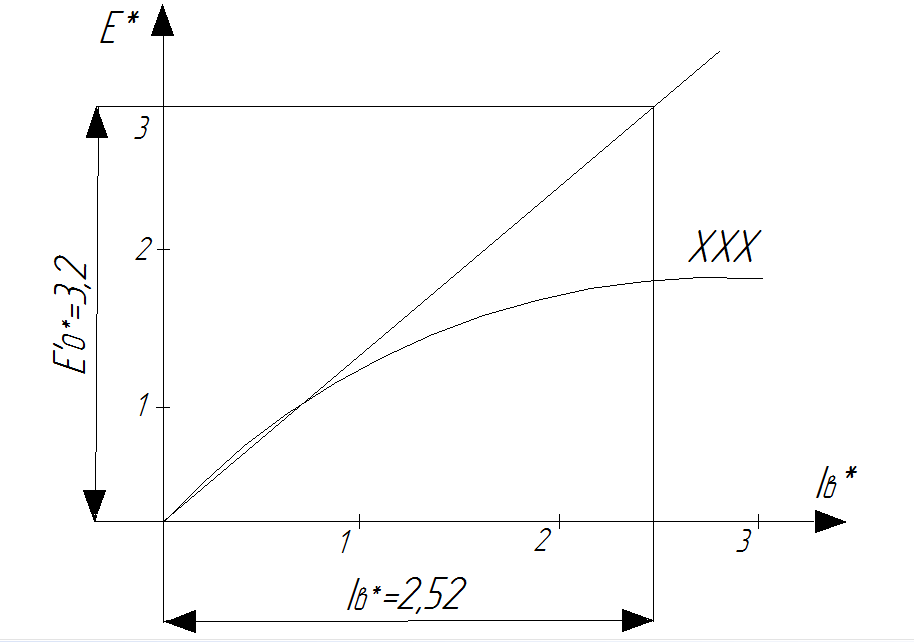 Рисунок 12.1 - Характеристика холостого хода. К расчёту кратности тока короткого замыкания при номинальном токе возбуждения 159 Кратность тока короткого замыкания при возбуждении холостого хода (ОКЗ) 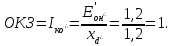 Величина Е′он* определяется по продолжению спрямлённой части характеристики холостого хода при Iв*= 1. 160 Кратность тока короткого замыкания при номинальном возбуждении 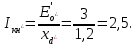 Величина Е′о* определяется по продолжению спрямлённой части характеристики холостого хода при номинальном токе возбуждения Iвн*= 2,52 (рисунок 12.1). 13 РАСЧЁТ И ПОСТРОЕНИЕ ХАРАКТЕРИСТИК ГЕНЕРАТОРА161 Угловая характеристика 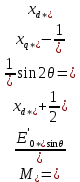 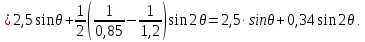 Статическая перегружаемость генератора определяется по угловой характеристике, рисунок 13.1, 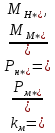 где 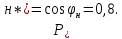 Из рисунка 13.1 Мм*=2,5, 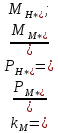 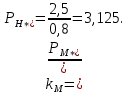 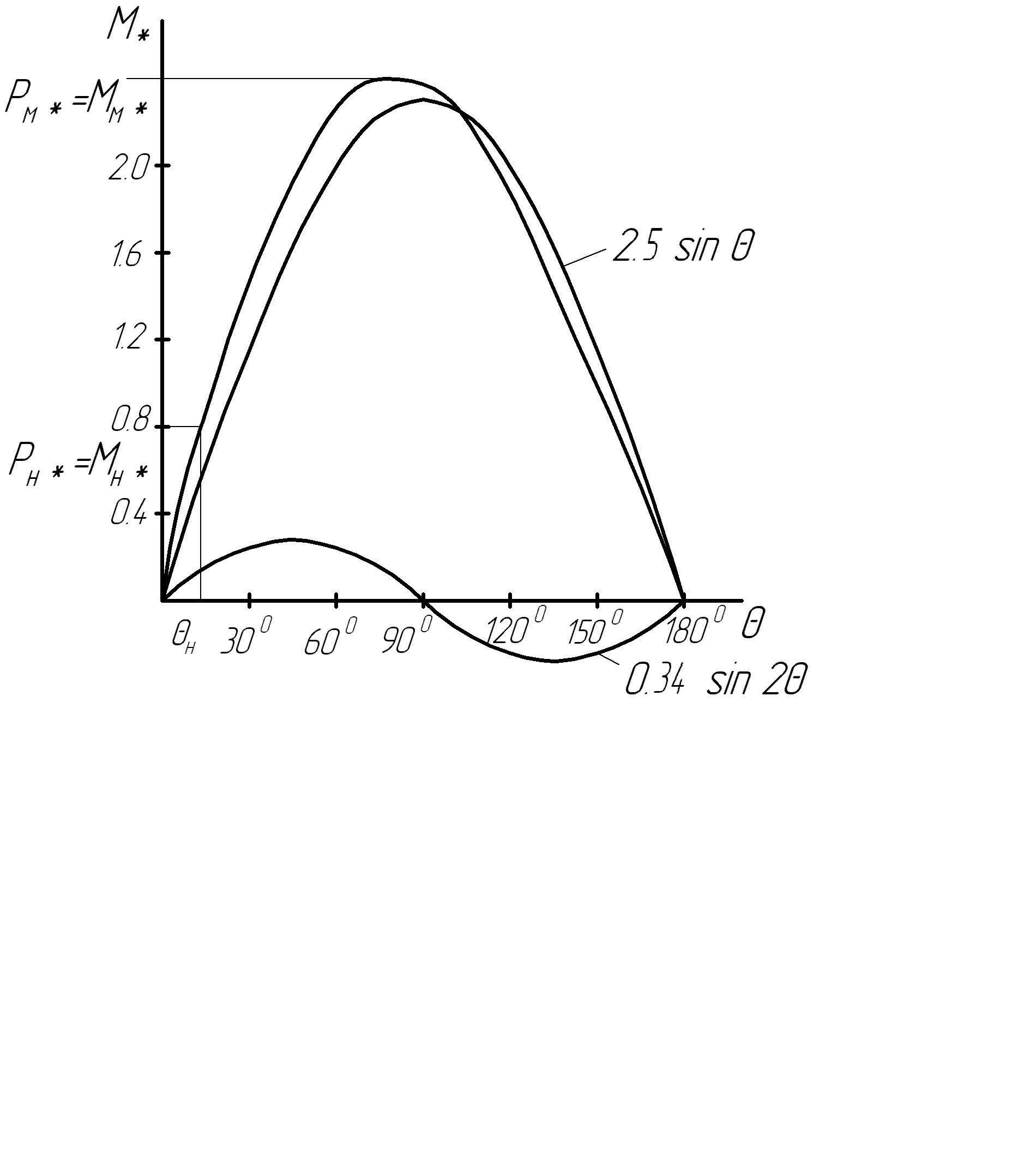 Рисунок 13.1 – Угловая характеристика 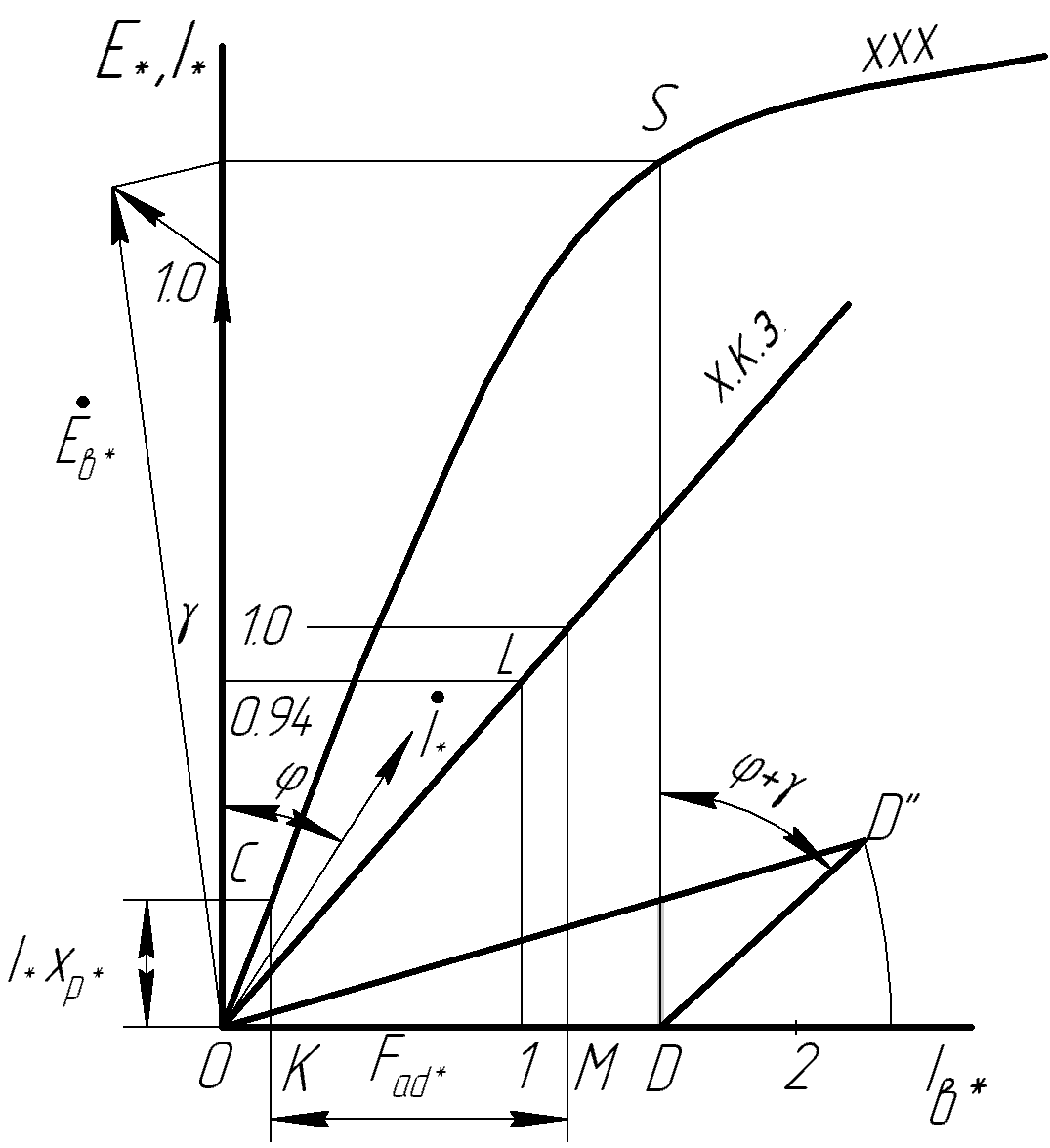 Рис. 13.2. Диаграмма Потье для 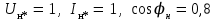 Опишем построение диаграммы Потье для случая U*=1; I*=1, cos φ = 0,8. На основании уравнения генератора 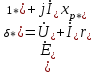 определяем вектор определяем вектор 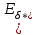 , как это было сделано при построении диаграммы Блонделя. , как это было сделано при построении диаграммы Блонделя.Пользуясь значением ЭДС 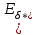 , по характеристике холостого хода находим ток возбуждения , по характеристике холостого хода находим ток возбуждения 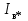 , необходимый для её создания (на рис. 13.2 отрезок OD). , необходимый для её создания (на рис. 13.2 отрезок OD).При построении диаграммы Потье применяют реактивное сопротивление Потье 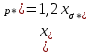 . Использование . Использование 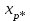 вместо вместо 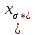 учитывает повышенное насыщение магнитной цепи индуктора от потока рассеяния возбуждения. МДС реакции якоря определяется по характеристике короткого замыкания, которую строим как прямую из начала координат через точку L, для которой учитывает повышенное насыщение магнитной цепи индуктора от потока рассеяния возбуждения. МДС реакции якоря определяется по характеристике короткого замыкания, которую строим как прямую из начала координат через точку L, для которой 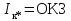 и и 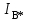 = 1. = 1.Для I* = 1 по характеристике короткого замыкания определяем МДС 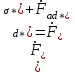 (отрезок 0М), отложив на оси ординат (отрезок 0М), отложив на оси ординат 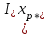 (отрезок 0К). Тогда (отрезок 0К). Тогда 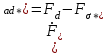 (отрезок КМ). (отрезок КМ).Чтобы получить МДС, соответствующую полному току возбуждения 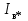 , необходимо геометрически сложить векторы , необходимо геометрически сложить векторы 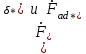 , при этом учитываем, что МДС , при этом учитываем, что МДС 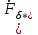 опережает опережает 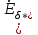 на 90°, а МДС на 90°, а МДС 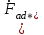 совпадает по направлению с током якоря совпадает по направлению с током якоря 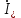 . Результирующий ток возбуждения находим, прибавляя к отрезку ОD отрезок DD' = КМ, причем КМ проводим под углом (φ+γ) к отрезку DS. . Результирующий ток возбуждения находим, прибавляя к отрезку ОD отрезок DD' = КМ, причем КМ проводим под углом (φ+γ) к отрезку DS.Принимая, что падение напряжения 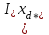 и реакция якоря и реакция якоря 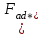 прямо пропорциональны току якоря, можно построить подобные диаграммы для различных значений тока I* , напряжения U* и cosφ. прямо пропорциональны току якоря, можно построить подобные диаграммы для различных значений тока I* , напряжения U* и cosφ.На рис. 11 построены диаграммы для U*, равных 1,0; 1,1; 1,15; cosφ=0,8. При этом принято, что 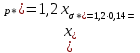 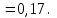 Падением напряжения на активном сопротивлении пренебрегаем. Данные построения сведены в табл. 13.1. Падением напряжения на активном сопротивлении пренебрегаем. Данные построения сведены в табл. 13.1.Таблица 13.1
По данным табл. 5 на рис. 12 построены регулировочные характеристики для напряжений U*, равных 1,0; 1,1; 1,15. 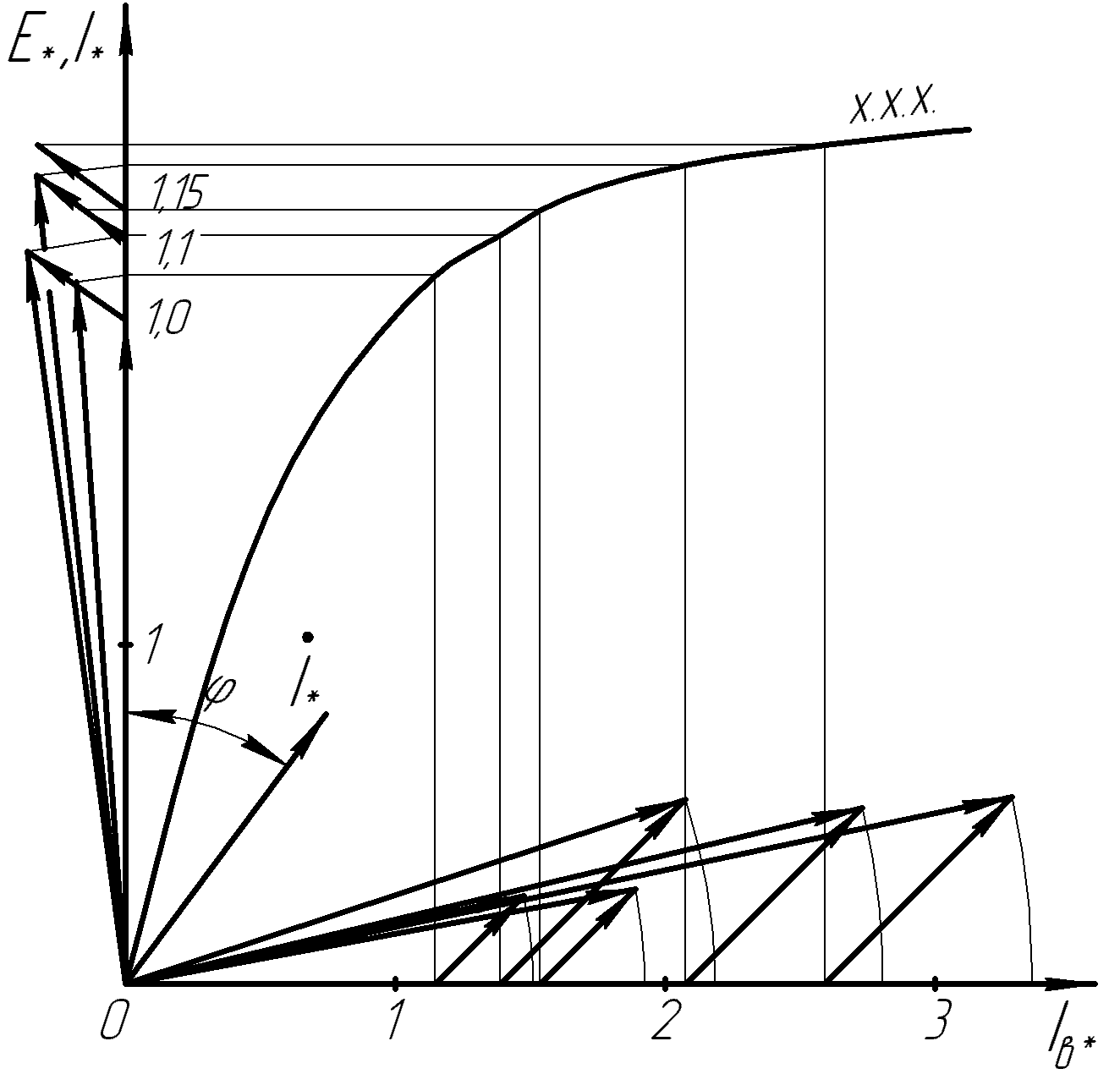 Рис. 13.3. Диаграмма Потье для построения регулировочных характеристик 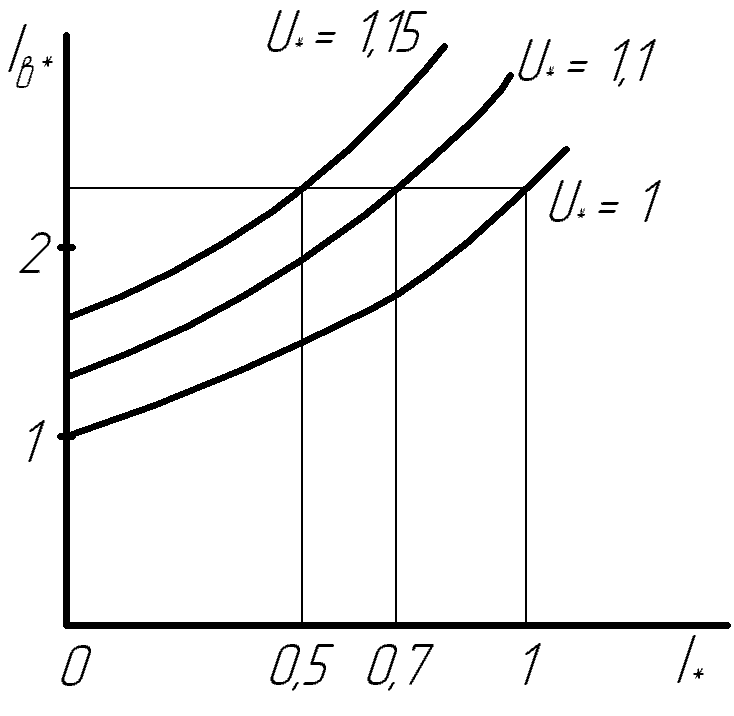 Рис. 13.4. Регулировочные характеристики 162. Внешняя характеристика U*= f(I*). Внешнюю характеристику можно построить, используя семейство регулировочных характеристик (рис. 13.4). Из точки, соответствующей U* = 1 и I* =1, проведем прямую параллельно оси абсцисс. Точки пересечения этой прямой с регулировочными характеристиками дадут значения тока I* при U* = 1,1 и U* = 1,15. Значение U* при I* =0 получим по характеристике холостого хода для Iвн*. Данные расчета сведены в табл. 13.2. Таблица 13.2
По данным табл. 13.2 на рис. 13.5 построена внешняя характеристика. 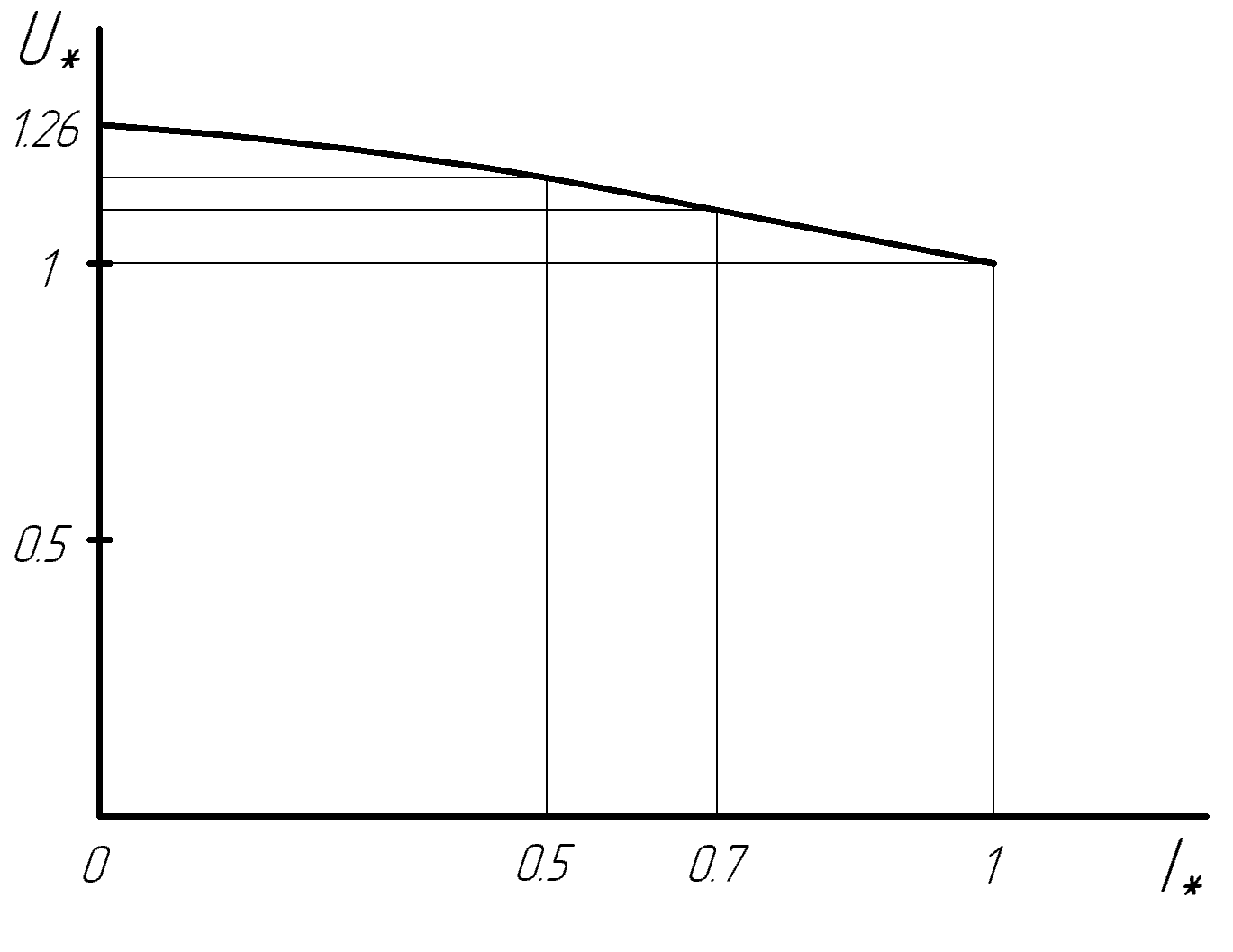 Рис. 13.5. Внешняя характеристика 163. U-образная характеристика I*=f( 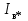 ). ).При построении U-образной характеристики должно быть обеспечено выполнение условий 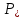 =const и =const и 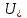 = const. Принимая во внимание, что = const. Принимая во внимание, что 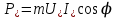 , можно отметить, что активная составляющая тока якоря , можно отметить, что активная составляющая тока якоря 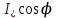 также постоянна. также постоянна.Для U-образной характеристики при U*=Uн* и Р*=Р*н=cosφ=0,8 активная составляющая тока 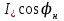 равна 0,8. Для характеристик при равна 0,8. Для характеристик при 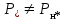 , например при , например при 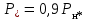 , активная составляющая , активная составляющая 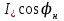 = 0,9·0,8 =0,72 и т.д. = 0,9·0,8 =0,72 и т.д. U-образную характеристику для случая Р*=0,8; U* =Uн* строим следующим образом. Откладываем по оси абсцисс в масштабе вектор напряжения 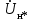 . С ним совпадает по направлению вектор активного тока Iн*cosφн (рис. 14). Затем задаемся несколькими значениями тока I*, например двумя I(1)* =1, I(2)* =0,9 для индуктивной нагрузки (φ>0), одним для активной нагрузки I(3)* = =Iн*cosφн и одним I(4)* =0,88 для емкостной нагрузки (φ<0), и размещаем их, как показано на рис. 13.6. Определяем для этих токов углы φ. . С ним совпадает по направлению вектор активного тока Iн*cosφн (рис. 14). Затем задаемся несколькими значениями тока I*, например двумя I(1)* =1, I(2)* =0,9 для индуктивной нагрузки (φ>0), одним для активной нагрузки I(3)* = =Iн*cosφн и одним I(4)* =0,88 для емкостной нагрузки (φ<0), и размещаем их, как показано на рис. 13.6. Определяем для этих токов углы φ.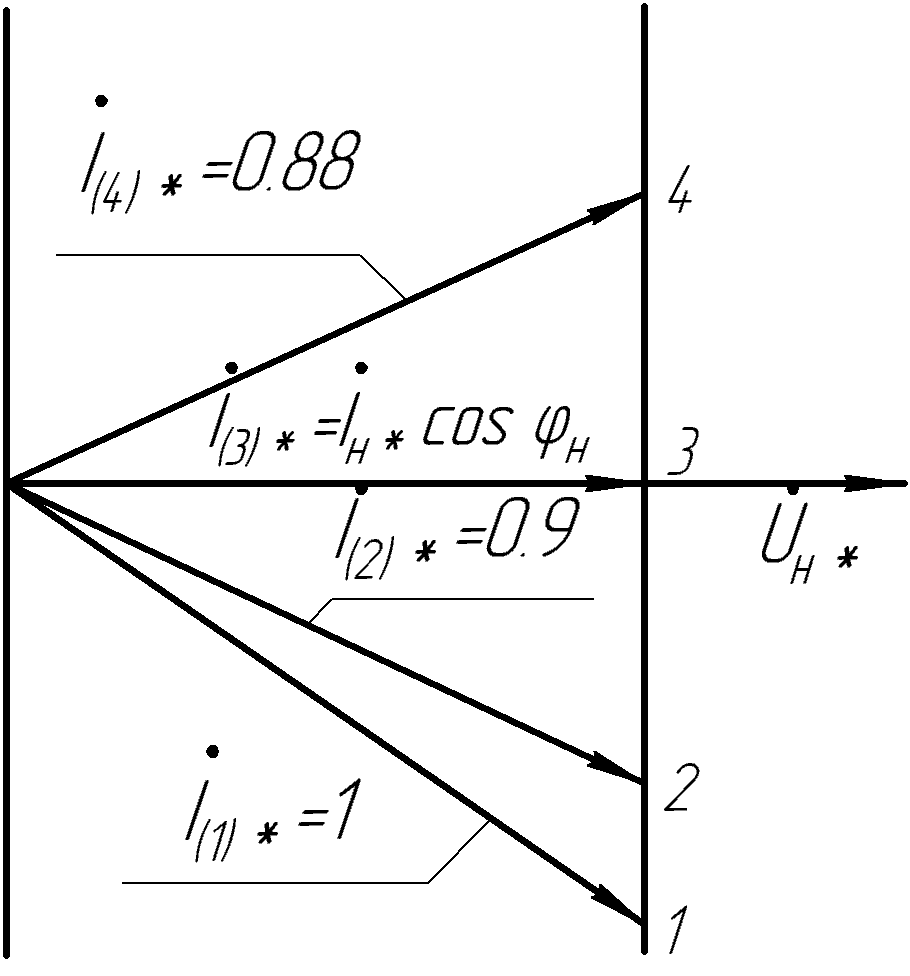 Рис. 13.6. Векторные диаграммы (к построению U-образной характеристики) 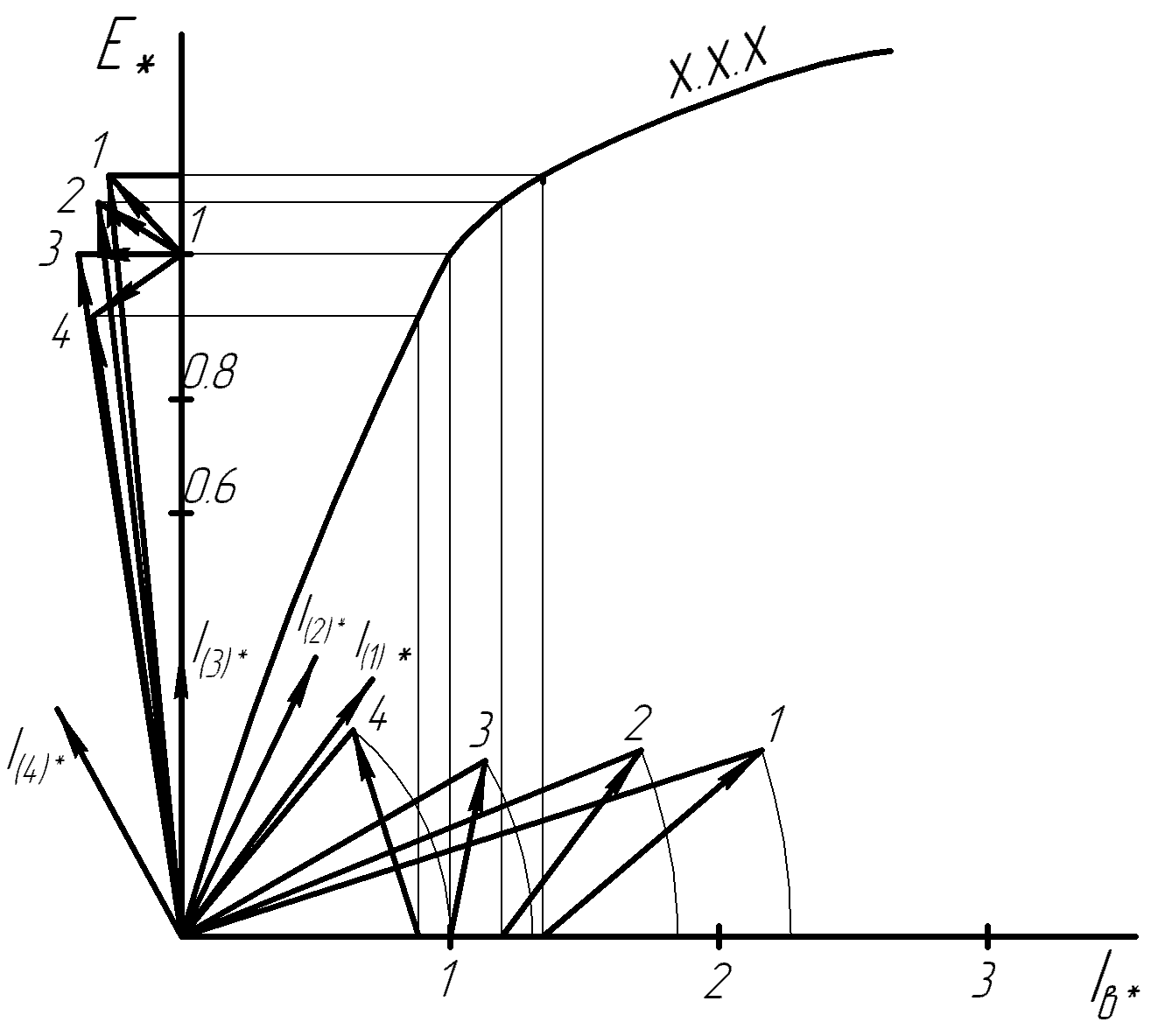 Рис. 13.7. Диаграмма Потье (к построению U-образной характеристики) Для каждого значения I(1,2,3,4)* и φ(1,2,3,4) строим диаграмму Потье, как это делалось при построении регулировочных характеристик (рис. 13.7). Данные расчёта сводим в табл. 13.3 Таблица 13.3
По данным табл. 13.3 строим U-образную характеристику (рис. 13.8). U-образная характеристика I*=f( 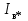 ) может быть построена без учёта насыщения магнитопровода. При этом будем считать синхронную машину неявнополюсной (аналогично допущению при построении диаграммы Потье) с синхронным индуктивным сопротивлением ) может быть построена без учёта насыщения магнитопровода. При этом будем считать синхронную машину неявнополюсной (аналогично допущению при построении диаграммы Потье) с синхронным индуктивным сопротивлением 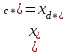 . Учтём ранее указанное соотношение . Учтём ранее указанное соотношение 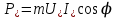 , откуда следует постоянство активной составляющей тока якоря , откуда следует постоянство активной составляющей тока якоря 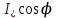 . С другой стороны, электромагнитная мощность неявнополюсной машины . С другой стороны, электромагнитная мощность неявнополюсной машины 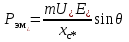 . Пренебрегая незначительной разницей между его выходной электрической и электромагнитной мощностями, будем считать, что выполнение условия постоянства мощности, необходимого для построения U-образной характеристики, обеспечивается также постоянством произведения . Пренебрегая незначительной разницей между его выходной электрической и электромагнитной мощностями, будем считать, что выполнение условия постоянства мощности, необходимого для построения U-образной характеристики, обеспечивается также постоянством произведения 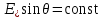 (т.к. остальные параметры формулы для определения (т.к. остальные параметры формулы для определения 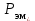 являются постоянными). Следствием полученных условий построения U-образной характеристики, а именно: являются постоянными). Следствием полученных условий построения U-образной характеристики, а именно: 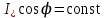 и и 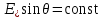 , является то, что конец вектора тока якоря при изменении угла φ перемещается вдоль линии тока I, а конец вектора ЭДС возбуждения – вдоль линии ЭДС E (рис.13.9). Промежуточные относительные значения тока якоря и возбуждения могут быть получены пропорциональным пересчётом соответствующих длин векторов тока якоря и ЭДС возбуждения по отношению к указанным величинам для базовой векторной диаграммы для номинального режима (на рис.13.9 базовая диаграмма 1 выделена утолщёнными линиями). С учётом допущения о неучёте насыщения можно считать , является то, что конец вектора тока якоря при изменении угла φ перемещается вдоль линии тока I, а конец вектора ЭДС возбуждения – вдоль линии ЭДС E (рис.13.9). Промежуточные относительные значения тока якоря и возбуждения могут быть получены пропорциональным пересчётом соответствующих длин векторов тока якоря и ЭДС возбуждения по отношению к указанным величинам для базовой векторной диаграммы для номинального режима (на рис.13.9 базовая диаграмма 1 выделена утолщёнными линиями). С учётом допущения о неучёте насыщения можно считать 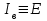 . В качестве примера на рис. 17 показано построение диаграмм для отстающего (1), активного (2) и опережающего (3) тока для номинальной мощности, а также для активного (2’) тока при 50 % процентной мощности. . В качестве примера на рис. 17 показано построение диаграмм для отстающего (1), активного (2) и опережающего (3) тока для номинальной мощности, а также для активного (2’) тока при 50 % процентной мощности. 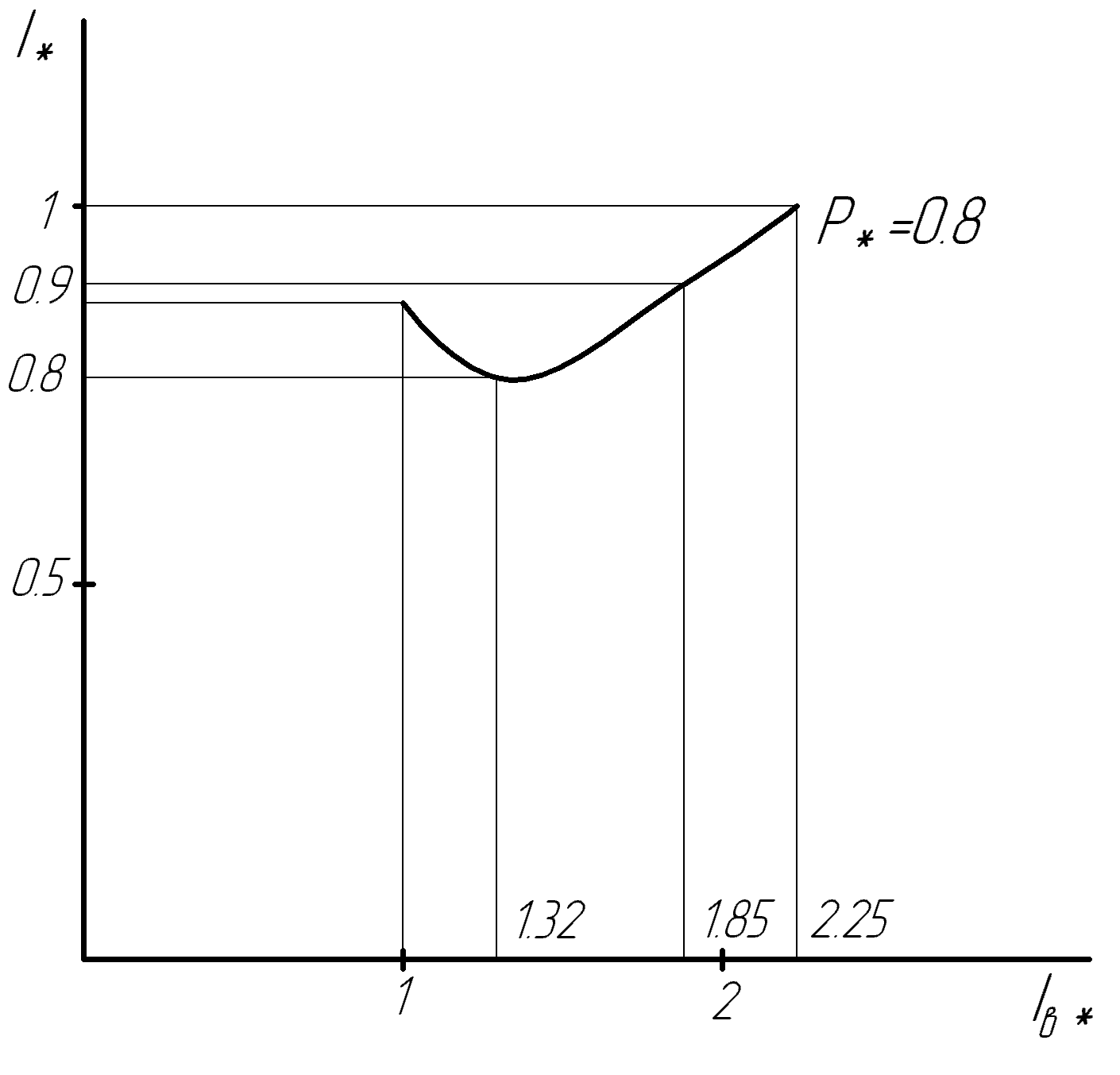 Рис. 13.8. U-образная характеристика 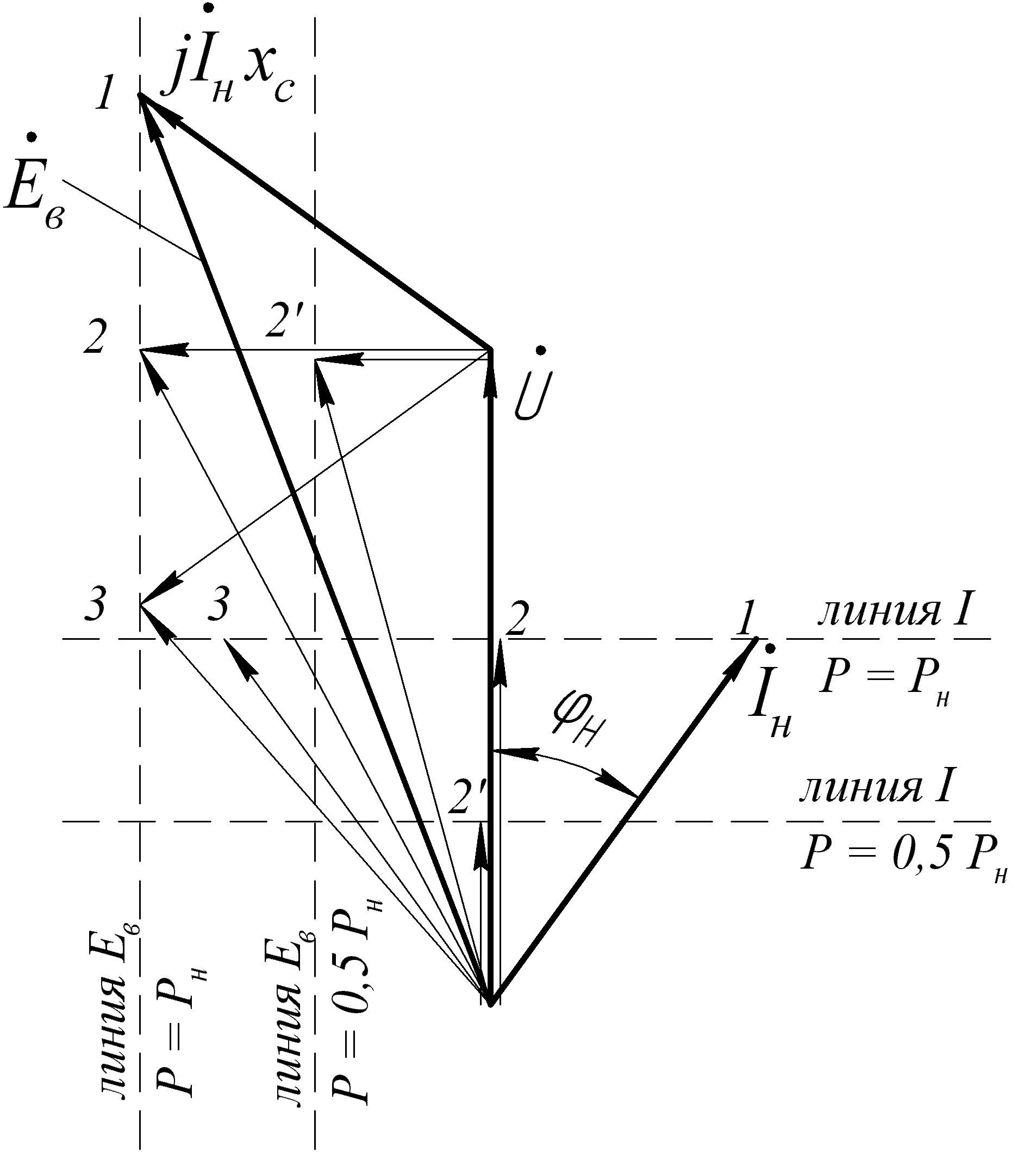 Рис. 13.9. Векторная диаграмма (к построению U-образной характеристики без учёта насыщения стали) ЗАКЛЮЧЕНИЕПроектирование электрической машины – задача неоднозначная, так как число исходных расчетных уравнений, описывающих электромагнитные связи в ней, меньше числа неизвестных величин. Потому номинальные данные могут быть обеспечены при различных соотношениях основных размеров и электромагнитных нагрузок машины. Оптимальный результат в значительной мере зависит от опыта проектировщика и достигается обычно при сопоставлении нескольких вариантов. В качестве универсального критерия оптимальности наиболее часто принимают минимум суммарных затрат, т.е. стоимость материалов, затрат на изготовление и эксплуатацию. Затраты на эксплуатацию, в свою очередь, зависят от КПД, коэффициента мощности, качества, ремонтопригодности и ряда других факторов. СПИСОК ЛИТЕРАТУРЫ1. Проектирование электрических машин: Учеб. пособие для вузов: В 2 кн./ И.П. Копылов, Б.К. Клоков, В.П.Морозкин и др.; Под. ред. И.П. Копылова.– 2-е изд., перераб. и доп. М.:Энергоатомиздат, 1993. Кн. 2. 384 с. 2. Буханцов Е.И. Методические указания к курсовому проекту по электрическим машинам. Синхронные генераторы/ НПИ. Новочеркасск, 1984. 48 с. 3. Буханцов Е.И. Методические указания. Пример расчёта синхронного генератора/ НПИ. Новочеркасск, 1985. 40 с. 4. Электротехнический справочник/ Под ред. П.Г. Грудинского, Г.Н. Петрова, М.И. Соколова, А.М. Федосеева, М.Г. Чиликина, И.В. Антика. Изд. 5–е. М.: Энергия, 1974. Т. 1. 775 с. 5. Видеман Е., Келлепбергер В. Конструкции электрических машин/Сокр. пер. с нем.; Под ред. Б.Н. Красовского. Л.: Энергия, 1972.; 520 с. 6. Виноградов Н.В. Производство электрических машин. М.: Энергия,1970. 288 с.    | |||||||||||||||||||||||||||||||||||||||||||||||||||||
