Выпарной аппарат. Проектирование выпарной установки для концентрированного водного раствора хлорида аммония, производительностью 22 кгс по концентрированному раствору
 Скачать 7.18 Mb. Скачать 7.18 Mb.
|
Таблица 3.2 - Температурный режим работы выпарной установки
3.3 Тепловой баланс выпарного аппарата 3.3.1 Расход теплоты на выпаривание Тепловая нагрузка 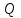 выпарного аппарата равна: выпарного аппарата равна: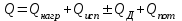 , (3.9) , (3.9)где 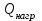 - расход теплоты на нагревание раствора, кВт; - расход теплоты на нагревание раствора, кВт; 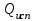 - расход теплоты на испарение влаги кВт; - расход теплоты на испарение влаги кВт; 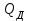 - теплота дегидратации. Обычно, эта величина мала по сравнению с другими статьями теплового баланса и ею можно пренебречь; - теплота дегидратации. Обычно, эта величина мала по сравнению с другими статьями теплового баланса и ею можно пренебречь;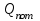 - расход теплоты на компенсацию потерь в окружающую среду. - расход теплоты на компенсацию потерь в окружающую среду.Расход теплоты на нагревание раствора 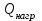 , определяется по формуле: , определяется по формуле: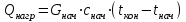 , (3.10) , (3.10)где 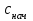 - теплоемкость разбавленного раствора, определяется по формуле: - теплоемкость разбавленного раствора, определяется по формуле: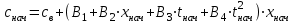 (3.11) (3.11)где 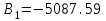 , , 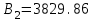 , , 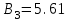 , , 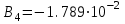 , , 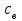 - удельная теплоемкость воды, определяется по формуле: - удельная теплоемкость воды, определяется по формуле: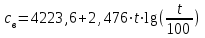 (3.12) (3.12)где 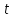 - температура воды, - температура воды,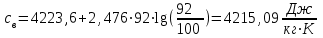 . .Тогда по формуле 3.11 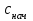 будет равна: будет равна: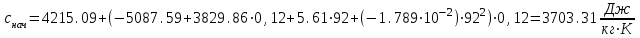 и по формуле 3.10 получим: и по формуле 3.10 получим: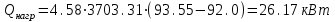 . .Расход теплоты на испарение определяется по формуле: 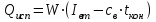 (3.13) (3.13)где 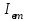 - энтальпия вторичного пара, - энтальпия вторичного пара, 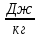 при температуре при температуре 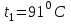 . .По (/1/, табл. LVI, стр. 548) находим 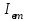 : :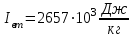 . .Теплоемкость воды по формуле 3.12 при температуре 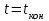 будет равна: будет равна: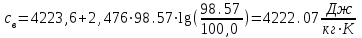 , ,тогда по формуле 3.13 находим расход теплоты на испарение: 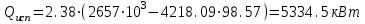 . .Расход теплоты на компенсацию потерь в окружающую среду 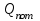 ,при расчете выпарных аппаратов принимают 3-5% от суммы ,при расчете выпарных аппаратов принимают 3-5% от суммы 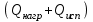 . Таким образом, . Таким образом, 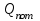 равняется: равняется: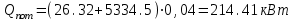 . .Следовательно, количество теплоты, передаваемой от греющего пара к кипящему раствору, по формуле 3.9 равняется: 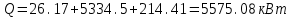 . .3.3.2 Определение расхода греющего пара Расход греющего пара 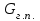 (в кг/с) в выпарном аппарате определяем по уравнению: (в кг/с) в выпарном аппарате определяем по уравнению: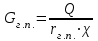 , (3.14) , (3.14)где 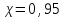 - паросодержание (степень сухости) греющего пара; - паросодержание (степень сухости) греющего пара; 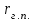 - удельная теплота конденсации греющего пара, - удельная теплота конденсации греющего пара, 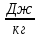 . Из (/1/, табл. LVII, стр. 550) находим для температуры . Из (/1/, табл. LVII, стр. 550) находим для температуры 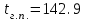 , , 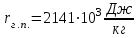 . .И получаем: 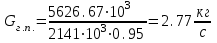 . .Удельный расход греющего пара: 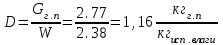 3.4 Расчет греющей камеры выпарного аппарата Выпарная установка работает при кипении раствора в трубах при оптимальном уровне. При расчете выпарного аппарата мы приняли высоту труб 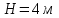 . При расчете установки мы приняли: тепловая нагрузка . При расчете установки мы приняли: тепловая нагрузка 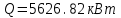 ; средняя температура кипения раствора хлорида аммония ; средняя температура кипения раствора хлорида аммония 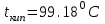 ; температура конденсации сухого насыщенного водяного пара ; температура конденсации сухого насыщенного водяного пара 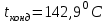 . Для кипящего раствора коэффициент теплопроводности раствора NH4Cl мы рассчитываем по формуле: . Для кипящего раствора коэффициент теплопроводности раствора NH4Cl мы рассчитываем по формуле: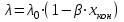 , (3.15) , (3.15)где 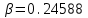 , , 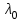 - коэффициент теплопроводности воды, - коэффициент теплопроводности воды, 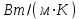 : :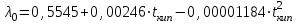 , (3.16) , (3.16)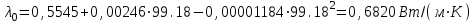 . .Тогда по формуле 2.15 получаем: 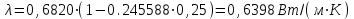 Средняя разность температур: 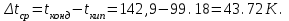 Находим коэффициент теплоотдачи от конденсирующегося водяного пара к поверхности вертикальных труб по формуле: 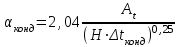 , (3.17) , (3.17)где 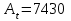 (/1/, табл. 4.6, стр. 162). (/1/, табл. 4.6, стр. 162).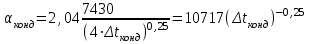 ; ;Следовательно, 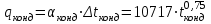 . .Коэффициент теплоотдачи от стенки труб к кипящему раствору: 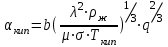 , (3.18) , (3.18)где 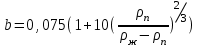 , (3.19) , (3.19)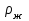 и и 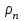 - соответственно плотности раствора и его пара при средней температуре кипения - соответственно плотности раствора и его пара при средней температуре кипения 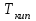 , К; , К; 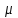 - динамический коэффициент вязкости, - динамический коэффициент вязкости, 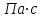 ; ; 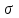 - поверхностное натяжение раствора, Н/м, при - поверхностное натяжение раствора, Н/м, при 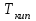 и и 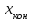 . .Плотность раствора, рассчитанная по формулам 3.6 и 3.7, равна: 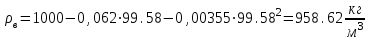 ; ;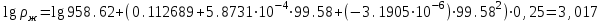 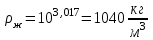 . .Плотность пара 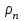 находим по (/1/, табл. LVI, стр. 548): находим по (/1/, табл. LVI, стр. 548):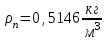 . .Таким образом, по формуле 3.19 получаем: 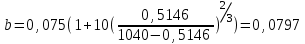 . .Динамический коэффициент вязкости рассчитывается по формуле: 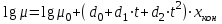 , (3.20) , (3.20)где 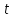 - температура раствора, - температура раствора,  , , 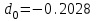 , , 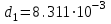 , , 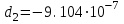 ; ; 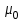 - вязкость воды, - вязкость воды, 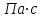 : :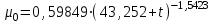 (3.21) (3.21)При средней температуре кипения раствора получаем: 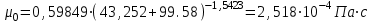 . .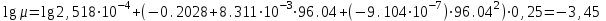 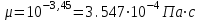 . .Поверхностное натяжение берем по (/1/, табл. XXIII, стр. 526) для хлорида аммония 10% концентрации: 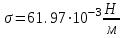 . .Подставляя найденные значения в формулу 3.18 получаем: 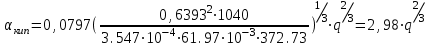 Принимаем тепловую проводимость загрязнений (/1/, табл. XXXI, стр. 531) стенки со стороны греющего пара 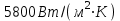 и со стороны кипящего раствора и со стороны кипящего раствора 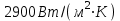 . Коэффициент теплопроводности стали по (/1/, табл. XXVIII, стр. 529) принимаем равным: . Коэффициент теплопроводности стали по (/1/, табл. XXVIII, стр. 529) принимаем равным: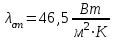 , ,по (/3/, табл. 2.2, стр. 16) толщину труб принимаем равной 2 мм. Тогда 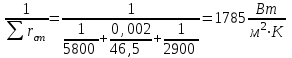 . .Ввиду того, что 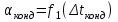 и и 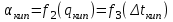 , для расчета коэффициента теплопередачи принимаем метод последовательных приближений. , для расчета коэффициента теплопередачи принимаем метод последовательных приближений.Для определения исходного значения 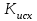 , учитывая: что при установившемся режиме теплопередачи , учитывая: что при установившемся режиме теплопередачи 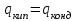 , выражаем , выражаем 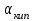 через через 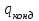 : :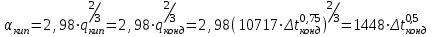 . .Затем рассчитываем исходные значения 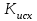 и и 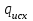 , принимая , принимая 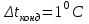 : :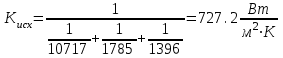 ; ;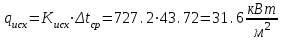 . .Находим значение 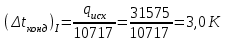 . .Составляем расчетную таблицу 3.3, в которую записываем исходные данные 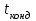 , , 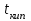 , , 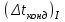 , , 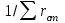 и результаты последующих расчетов. и результаты последующих расчетов.Таблица 3.3 Температурный режим работы выпарной установки
Первое приближение: 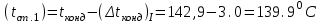 ; ;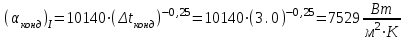 ; ;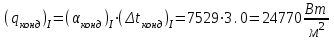 ; ;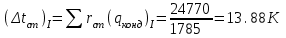 ; ;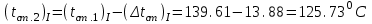 ; ;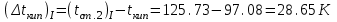 ; ;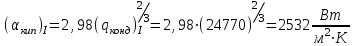 ; ;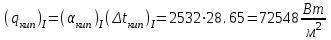 . .В первом приближении: 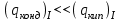 . .II. Второе приближение. Рассчитываем по первому приближению 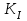 : :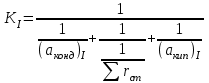 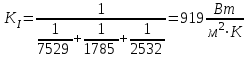 , ,тогда 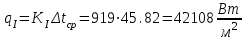 . .Величину 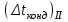 определяем, принимая определяем, принимая 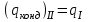 при при 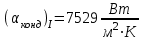 : :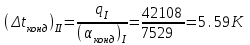 . .Затем выполняем аналогичный расчет (см. строку II в табл. 3.3). Расхождение 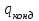 и и 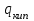 по второму расчету: по второму расчету: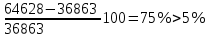 . .III. Третье приближение. Рассчитываем по второму приближению 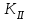 : :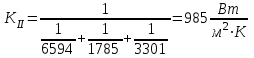 , ,тогда 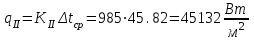 . .Величину 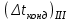 определяем, принимая определяем, принимая 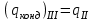 при при 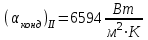 : :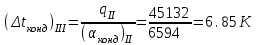 . .Затем выполняем аналогичный расчет (см. строку III в табл. 3.3). Расхождение 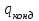 и и 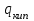 по третьему расчету: по третьему расчету: 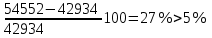 . .По результатам расчетов второго и третьего приближения строим график 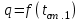 . Полагая что при малых изменениях температуры поверхностные плотности . Полагая что при малых изменениях температуры поверхностные плотности 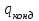 и и 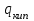 линейно зависят от линейно зависят от 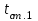 , графически определяем , графически определяем 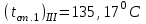 Графическая зависимость Графическая зависимость 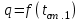 IV. Проверочный расчет (см. табл. 3.3). Расчеты аналогичны расчетам первого приближения. Расхождение 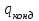 и и 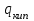 : :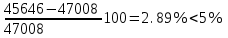 По данным последнего приближения определяем коэффициент теплопередачи: 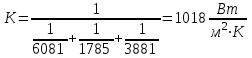 . .Площадь поверхности теплопередачи: 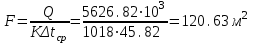 . .По (Таблице 2.2 стр. 16) принимаем аппарат Тип 1, Исполнение 2, группа А (С выносной греющей камерой и кипением в трубах), с площадью поверхности теплопередачи 132  (действительная), Трубы 38 х 2 мм, длинной Н = 4000 мм , т.е. с запасом (действительная), Трубы 38 х 2 мм, длинной Н = 4000 мм , т.е. с запасом 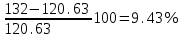 . .3.5 Полный тепловой расчет подогревателя начального раствора 3.5.1 Ориентировочный расчет теплообменного аппарата для подогрева раствора 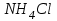 перед подачей в выпарной аппарат перед подачей в выпарной аппаратТаблица 3.4 - Основные данные для расчета подогревателя
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

