Выпарной аппарат. Проектирование выпарной установки для концентрированного водного раствора хлорида аммония, производительностью 22 кгс по концентрированному раствору
 Скачать 7.18 Mb. Скачать 7.18 Mb.
|
|
Значение усредненной по всей теплообменной поверхности разности температур рассчитывается по формуле: 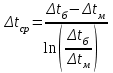 ; (3.22) ; (3.22)при этом 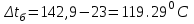 ; ;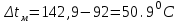 . .Получаем 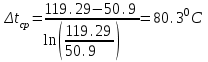 . .Средняя температура раствора 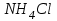 : :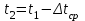 , ,где 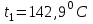 - среднее арифметическое значение температуры теплоносителя, которое изменяется на меньшую величину (в данном случае температура конденсации греющего пара); - среднее арифметическое значение температуры теплоносителя, которое изменяется на меньшую величину (в данном случае температура конденсации греющего пара);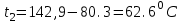 . .Расход раствора 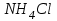 : :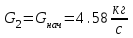 . .Расход теплоты на нагрев раствора: 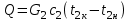 , (3.23) , (3.23)где 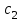 - удельная теплоемкость раствора, рассчитанная по формуле 2.11, при - удельная теплоемкость раствора, рассчитанная по формуле 2.11, при 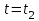 и и 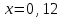 % масс. % масс.По формуле 3.12 удельная теплоемкость воды при 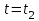 равна: равна: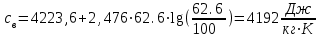 . .Тогда по формуле 3.11 получаем: 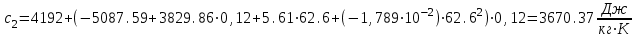 Расход теплоты на нагрев раствора по формуле 3.23 равен: 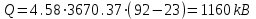 . .Расход греющего пара: 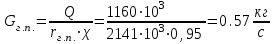 Принимая по (/1/, табл. 4.8 стр. 172) ориентировочный коэффициент теплопередачи 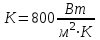 , (аппарат со свободной циркуляцией, передача тепла от конденсирующегося пара к воде), рассчитываем ориентировочную поверхность теплопередачи: , (аппарат со свободной циркуляцией, передача тепла от конденсирующегося пара к воде), рассчитываем ориентировочную поверхность теплопередачи: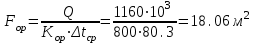 . .Проходное сечение 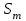 трубного пространства рассчитываем по формуле: трубного пространства рассчитываем по формуле: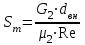 , (3.24) , (3.24)где 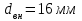 - внутренний диаметр труб; - внутренний диаметр труб; 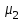 - динамический коэффициент вязкости начального раствора при средней температуре - динамический коэффициент вязкости начального раствора при средней температуре 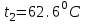 ; Re – критерий Рейнольдса. ; Re – критерий Рейнольдса.По формуле 3.21 при 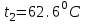 для воды получаем: для воды получаем: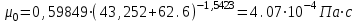 , ,а по формуле 3.20 для раствора находим: 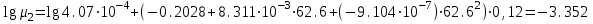 , ,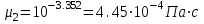 Для обеспечения интенсивного теплообмена подбираем аппарат с турбулентным режимом течения теплоносителей. Раствор направляется в трубное пространство, греющий пар – в межтрубное. Максимальное проходное сечение 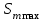 считаем при критерии Рейнольдса считаем при критерии Рейнольдса 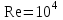 : :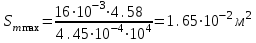 , ,минимальное – при 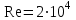 : :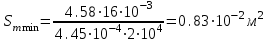 . .По полученному оценочному значению поверхности теплопередачи 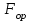 с учетом с учетом 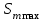 и и 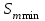 , в качестве подогревателя, мы выбираем по (/3/ табл. 1.2 стр. 6) 2-у ходовый теплообменник, с внутренним диаметром кожуха , в качестве подогревателя, мы выбираем по (/3/ табл. 1.2 стр. 6) 2-у ходовый теплообменник, с внутренним диаметром кожуха 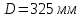 , числом труб , числом труб 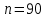 , поверхностью теплообмена , поверхностью теплообмена 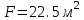 , длиной труб , длиной труб 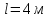 , проходным сечением , проходным сечением 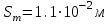 и числом рядов труб и числом рядов труб 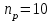 , расположенных в шахматном порядке. , расположенных в шахматном порядке.3.5.2 Подробный расчет теплообменного аппарата 3.5.2.1 Теплоотдача в трубах Находим, что теплоотдача для раствора 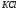 описывается уравнением: описывается уравнением: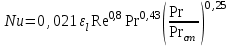 , (3.25) , (3.25)где 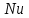 - критерий Нуссельта; - критерий Нуссельта; 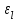 - поправочный коэффициент; Re – критерий Рейнольдса; Pr – критерий Прандтля; - поправочный коэффициент; Re – критерий Рейнольдса; Pr – критерий Прандтля; 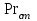 - критерий Прандтля при температуре стенки трубы. - критерий Прандтля при температуре стенки трубы.Коэффициент 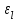 примем равным 1, полагая, что примем равным 1, полагая, что 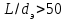 (/1/, табл. 4.3, стр. 153), где (/1/, табл. 4.3, стр. 153), где 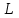 - длина труб, - длина труб, 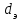 - эквивалентный диаметр. Критерий Рейнольдса рассчитываем по формуле: - эквивалентный диаметр. Критерий Рейнольдса рассчитываем по формуле: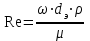 , (3.26) , (3.26)где 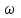 - средняя скорость потока, - средняя скорость потока, 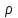 и и 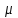 - соответственно плотность раствора и динамический коэффициент вязкости, при средней температуре - соответственно плотность раствора и динамический коэффициент вязкости, при средней температуре 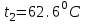 . . По формуле 3.7 плотность раствора при 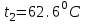 и и 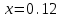 % масс. равняется: % масс. равняется: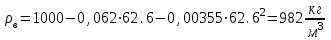 , ,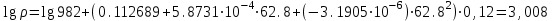 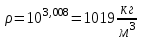 . .Среднюю скорость потока определяем по формуле: 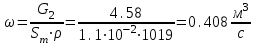 Учитывая, что для труб круглого сечения диаметр труб и эквивалентный диаметр совпадают, то для труб 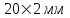 получаем: получаем: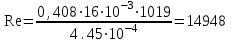 . .Критерий Прандтля находим по формуле: 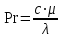 , (3.27) , (3.27)где 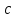 - удельная теплоемкость, - удельная теплоемкость, 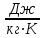 ; ; 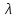 - коэффициент теплопроводности, - коэффициент теплопроводности, 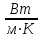 ; ; 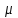 - динамический коэффициент вязкости, - динамический коэффициент вязкости, 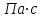 . . Коэффициент теплопроводности при 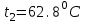 и и 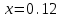 % масс. по формуле 3.15 равняется: % масс. по формуле 3.15 равняется: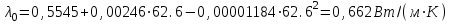 , ,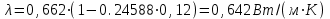 . .Таким образом, критерий Pr при 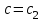 и и 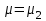 равняется: равняется: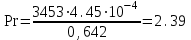 Коэффициент теплоотдачи от раствора к стенке: 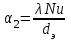 . .С учетом формулы 3.25 получаем: 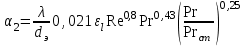 , (3.28) , (3.28)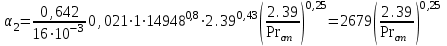 . .3.5.2.2 Теплоотдача при пленочной конденсации водяного пара Для водяного пара в случае конденсации на пучке горизонтальных труб осредненный по всему пучку коэффициент теплопередачи 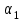 можно рассчитать по формуле: можно рассчитать по формуле: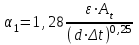 , (3.29) , (3.29)где 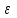 - поправочный множитель, учитывающий влияние числа труб по вертикали; - поправочный множитель, учитывающий влияние числа труб по вертикали; 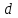 - наружный диаметр труб; - наружный диаметр труб; 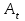 =7430 (взято из /1/, табл.4.6, стр. 162 при температуре конденсации греющего пара); =7430 (взято из /1/, табл.4.6, стр. 162 при температуре конденсации греющего пара); 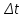 - разность средней температуры конденсации греющего пара - разность средней температуры конденсации греющего пара 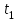 и температуры стенки со стороны греющего пара и температуры стенки со стороны греющего пара 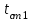 : :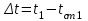 . .Поправочный множитель 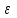 находим по (/1/, рис. 4.7, стр. 162) для шахматного расположения труби при числе рядов труб по вертикали находим по (/1/, рис. 4.7, стр. 162) для шахматного расположения труби при числе рядов труб по вертикали 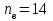 : :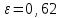 . .Имеем: 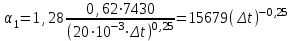 . .3.5.2.3 Расчет коэффициента теплопередачи Первое приближение. Принимаем в первом приближении 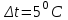 . Тогда температура стенки со стороны греющего пара равняется: . Тогда температура стенки со стороны греющего пара равняется: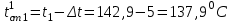 . .Тогда по формуле (3.29) получаем: 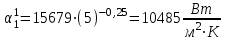 . .При этом удельный тепловой поток от пара к стенке равен: 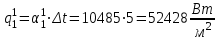 . .Сумма термических сопротивлений равна: 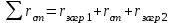 , ,где 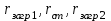 - соответственно термические сопротивления загрязнений со стороны греющего пара, стенки и со стороны раствора. - соответственно термические сопротивления загрязнений со стороны греющего пара, стенки и со стороны раствора.По (/1/, табл. XXXI, стр. 531) находим: 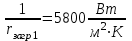 , , 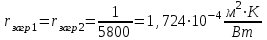 . .Для стенки: 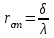 , ,где 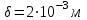 - толщина стенки, - толщина стенки, 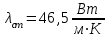 - коэффициент теплопроводности стали (/1/, табл. XXVIII, стр. 529). - коэффициент теплопроводности стали (/1/, табл. XXVIII, стр. 529).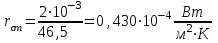 , ,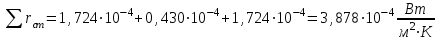 . .Поскольку удельный тепловой поток от пара к стенке 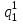 равен удельному тепловому потоку через стенку равен удельному тепловому потоку через стенку 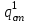 , то можно получить: , то можно получить: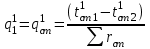 , ,при этом 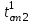 - температура стенки со стороны раствора равна: - температура стенки со стороны раствора равна: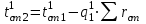 , ,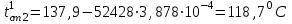 . .При температуре 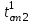 удельная теплоемкость, динамический коэффициент вязкости и коэффициент теплопроводности, вычисленные, соответственно, по формулам 3.11, 3.15, 3.20 равны: удельная теплоемкость, динамический коэффициент вязкости и коэффициент теплопроводности, вычисленные, соответственно, по формулам 3.11, 3.15, 3.20 равны: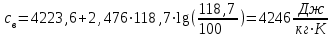 , ,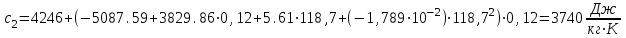 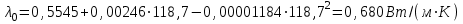 , ,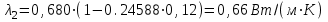 ; ;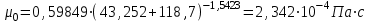 , ,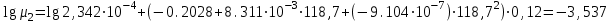 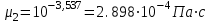 . .Подставляя найденные значения в формулу 3.27, получаем значение критерия Прандтля при температуре стенки: 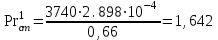 . .По формуле 3.28 находим в коэффициент теплоотдачи от раствора к стенке: 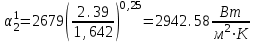 . .Тогда удельный тепловой поток от стенки к раствору равняется: 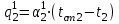 , ,где 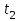 - вычисленная ранее средняя температура раствора. - вычисленная ранее средняя температура раствора.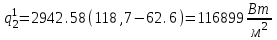 . .Расхождение между 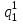 и и 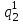 в первом приближении составляет в первом приближении составляет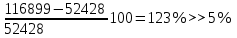 . .Составляем таблицу 3.4, в которую заносим результаты первого и второго приближений , а также проверочный расчет. Таблица 3.5
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

