Проектная работа по теме Графы. Графы. Проектная работа по теме Графы 20212022 уч г. Содержание проекта
 Скачать 415.13 Kb. Скачать 415.13 Kb.
|
|
Проектная работа по теме Графы 2021-2022 уч.г. Содержание проекта
Актуальность выбранной темы Теория графов – наука сравнительно молодая. «Графы» имеют корень греческого слова «графо», что значит «пишу». Тот же корень в словах «график», «биография». Теория графов является частью как топологии, так и комбинаторики. Свойства независимости графа свидетельствуют о том, что это топологическая теория. А удобство формулировок комбинаторных задач в терминах графов привело к тому, что теория графов стала одним из самых мощных приемов комбинаторики. Решение большинства комбинаторных задач значительно упрощается, используя концепцию графа. Использование теории графов при работе с логическими задачами значительно упрощает их решение и делает его более наглядным и интересным. Помимо школьных знаний элементы теории графов нашли свое применение и в жизненных, бытовых ситуациях. Напрашивается вывод о том, что теория графов способствуют развитию мышления и интеллекта. Поэтому тема выбранная мною актуальна и интересна. Цель и задачи проекта Цель проекта изучить понятие граф и его элементы, продемонстрировать решение задач с помощью графов. Для достижения цели, были поставлены следующие задачи: Изучить и проанализировать литературу по теме исследования, рассмотреть основные понятия. Подобрать задачи и показать, что используя понятие граф можно упростить и рационально решать многие логические задачи. Продемонстрировать с помощью графа, желание одноклассников сидеть друг с другом. Сделать выводы по результатам проведённого исследования. 3. Методы исследования, объект исследования В своём проекте я использовал следующие методы исследования: Самостоятельная работа с источниками информации (чтение книг, поиск в интернете) и наблюдение; Эксперимент; Обобщение полученных результатов. Объектом исследования моего проекта стали логические задачи, решаемы с помощью графов. 4. Основные проблемные вопросы, гипотеза Перед собой я поставил несколько проблемных вопросов, на которые планирую получить ответы в результате моих исследований. Что такое граф и его основные свойства и виды? Действительно ли с помощью графов можно упростить и рационально решать многие логические задачи? Как с помощью графа показать желание учащихся сидеть друг с другом? Где в повседневной жизни можно использовать знания о графах? Гипотезы: предположим, что с помощью графов можно упростить и рационально решать многие логические задачи; на графе можно наглядно показать желание учащихся сидеть друг с другом. 5. Теоретическая часть 5.1 Понятие графа Первая работа по теории графов принадлежит Леонарду Эйлеру. Она появилась в 1736 году в публикациях Петербургской Академии Наук и начиналась с рассмотрения задачи о кенигсбергских мостах. Через город Кенигсберг протекает река Преголя. Она делится на два рукава и огибает остров. В 17 веке в городе было семь мостов, расположенных так, как показано на рисунке. 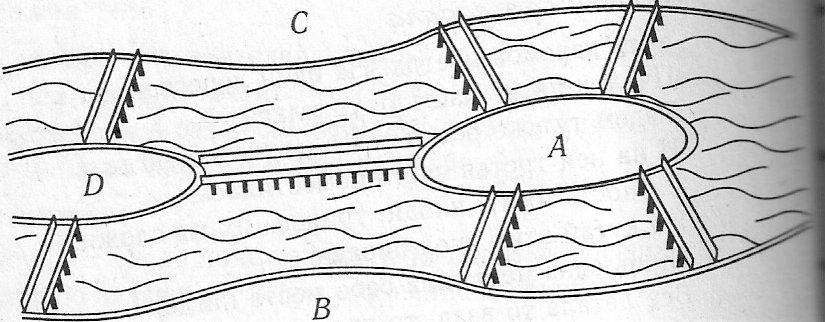 Рассказывают, что однажды житель города спросил у своего знакомого, сможет ли он пройти по всем мостам так, чтобы на каждом из них побывать только один раз и вернуться к тому месту, откуда началась прогулка. Многие горожане заинтересовались этой задачей, однако придумать решение никто не смог. Этот вопрос привлек внимание ученых из многих стран. Разрешить проблему удалось известному математику Леонарду Эйлеру, уроженец города Базеля родился 15 апреля, 1707 года. Леонард Эйлер не только решил эту конкретную задачу, но и придумал общий метод решения подобных задач. Эйлер поступил следующим образом: он «сжал» сушу в точки, а мосты «вытянул» в линии. В результате получилась фигура, изображенная на рисунке. 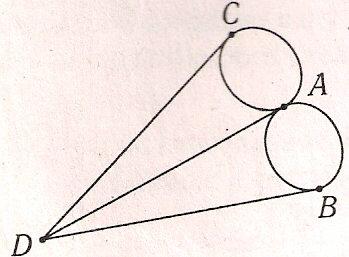 Такую фигуру, состоящую из точек и линий, связывающих эти точки, называют графом. Точки A,B,C,D называют вершинами графа, а линии, которые соединяют вершины – ребра графа. Степенью вершины называется число ребер графа, которым принадлежит эта вершина.На рисунке из вершин B,C,D выходят по 3 ребра, следовательно, степень вершин равна 3, а из вершины A – 5 ребер, значит степень вершины – 5. Вершины, из которых выходит нечетное число ребер, называют нечетными вершинами, а вершины, из которых выходит четное количество ребер – четными. 5.2 Виды графов Граф называется двудольным, если его вершины можно разбить на две группы (две доли) так, что каждое ребро в этом графе соединяет вершины, принадлежащие разным группам. Двудольный граф удобно изображать, нарисовав отдельно вершины двух долей. Например: На школьном балу каждый мальчик станцевал с тремя девочками, а каждая девочка — с четырьмя мальчиками. Этот граф может выглядеть следующим образом: 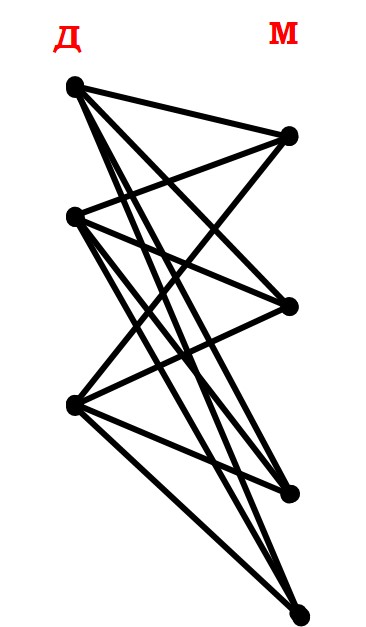 Эйлеров граф – граф, в котором содержится цикл, включающий все ребра графа ровно один раз, иначе говоря, граф, который можно нарисовать, не отрывая карандаша от бумаги. Граф считается Эйлеровим тогда и только тогда когда степень каждой его вершины четная. Приведем пример такого графа на рисунке. 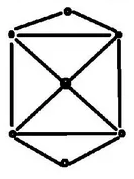 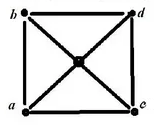 Эйлеров граф Не Эйлеров граф Граф называется связным, если любые две его вершины могут быть соединены путем, т. е. последовательностью ребер, каждое следующее из которых начинается в конце предыдущего. Граф называется несвязным, если это условие не выполняется. Деревом называется связный граф без циклов. Приведем пример такого графа на рисунке. 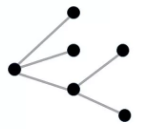 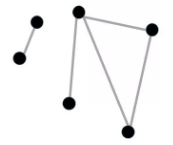 Дерево Не дерево 5.3 Свойства графов 1. Если все вершины графа четные, то можно одним росчерком (т.е. не отрывая карандаша от бумаги и не проводя дважды по одной и той же линии) начертить граф. При этом движение можно начать с любой вершины и окончить в той же вершине. 2. Граф с двумя нечетными вершинами тоже можно начертить одним росчерком. Движение нужно начинать от любой нечетной вершины, а заканчивать на другой нечетной вершине. 3. Граф с более чем двумя нечетными вершинами невозможно начертить одним росчерком. 4. Число нечетных вершин графа всегда четное. 5. Если в графе имеются нечетные вершины, то наименьшее число росчерков, которыми можно нарисовать граф будет равно половине числа нечетных вершин этого графа. 6. Практическая часть 6.1. Подтверждение первой гипотезы Задача 1. В 6 классе решили провести соревнования по игре «Морской бой». В нем приняли участие 6 учащихся: Артем, Борис, Виктория, Глеб, Диана и Екатерина. Соревнования проводятся по круговой системе, то есть каждый должен сыграть по одной партии со всеми участниками. К настоящему моменту несколько игр уже было сыграно. Известно, что Артем сыграл с Борисом, Глебом и Екатериной. Борис – с Артемом и Глебом. Виктория сыграла с Глебом, Дианой и Екатериной. Глеб – с Артемом, Викторией и Борисом. Сколько игр проведено к настоящему моменту и сколько ещё осталось? Решение: Построим граф, где вершины будут ребята, а ребра - партии. Синим цветом обозначим ребра – сыгранных партий. Так как ребята играют в круговую, то степень каждой вершины должна равняться 5. Дополним граф недостающими ребрами и обозначим их красным цветом.  Подсчитаем количество ребер каждого цвета: 7 синих, 8 красных, следовательно, 7 партий сыграно, 8 еще предстоит сыграть. Ответ: 7 партий сыграно, 8 еще предстоит сыграть. Задача 2. Десять хулиганов кидали снежки в окна школы. Первый хулиган попал в окно ровно 1 раз, второй — ровно 2 раза, …, десятый — ровно 10 раз, причём никакой хулиган не попал в одно и то же окно дважды. В каждое школьное окно либо попали снежком 5 раз, либо не попали вовсе. Сколько школьных окон пострадали от снежков? Решение: Составим двудольный граф, в котором левая доля содержит столько вершин, сколько хулиганов – 10. Количество вершин правой доли графа соответствует количеству пострадавших окон, так как эта величина не известна, обозначим ее за а. Если хулиган попал в окно, то соответствующие вершины будем соединять ребром. Тогда каждая вершина левой доли будет иметь степень 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, что соответствует количеству попаданий в окно каждым хулиганом. Соединять вершины ребрами начнем с вершины степень, которой равна 10. При этом будем учитывать, что степень вершины правой доли равна 5, так как в каждое окно по условию задачи попали ровно 5 раз. Соединяя соответствующие вершины ребрами, мы видим, что для выполнения всех условий в правой доле графа достаточно 11 вершин, а следовательно пострадавших окон от снежков тоже 11. 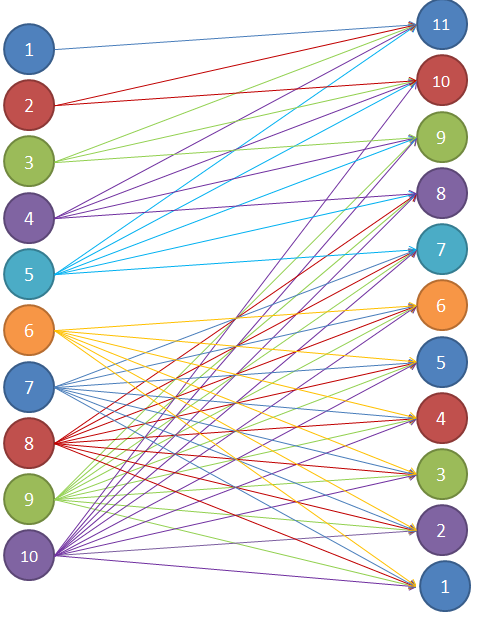 Проверить верность найденного решения, можно составив уравнение: 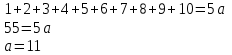 Ответ: 11 окон. Задача 3. Ученики 6 класса приехали на экскурсию в Москву. По программе учащиеся должны посетить значимые места в следующем порядке: Красная площадь, ГУМ, Музей Московского Кремля, Мавзолей В. И. Ленина, Александровский сад, ВДНХ, Музей космонавтики, Останкинская телебашня, Нескучный сад, Московский планетарий. Что бы успеть посетить все достопримечательности они составили карту, на которой указали важные места и дороги как к ним добраться. Установите, какому месту соответствуют буквы на карте, если учащиеся ни по одной дороге не проезжали более одного раза. 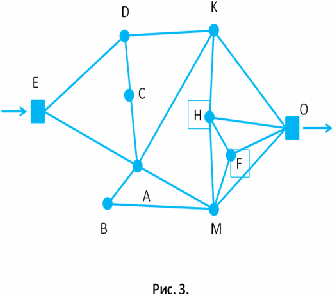 Решение: На карте видно, что экскурсия ребят началась с пункта Е и закончилась в О. В места В и С ведут только две дороги, значит по учащиеся должны были проехать по ним. Определены участки маршрута, проходящие через А: АС и АВ. По дорогам АЕ, АК и АМ ученики 6 класса не ездили, следовательно, перечеркнем их. Отметим жирной линией ЕD и перечеркнем DK. Перечеркнем МО и МН, а MF отметим жирной линией, значит, перечеркнем FHO. Линии FH, HK и КО отметим жирным. Найдем единственно возможный при данном условии маршрут. С рисунка остается только считать ответ. Ответ: Е – Красная площадь, D - ГУМ, С – Музей Московского Кремля, А – Мавзолей В.И. Ленина, В – Александровский сад, М – ВДНХ, F – Музей космонавтики, Н – Останкинская телебашня, К – Нескучный сад, О – Московский планетарий. Приведенные задачи, демонстрируют, что использование графов упрощают процесс их решения, делая его более наглядным и интересным. 6.2. Подтверждение второй гипотезы Изучая Теорию Графов, мне стало интересно, как можно с их помощью графически изобразить желание учащихся сидеть друг с другом. Я провел опрос среди одноклассников, в котором они ответили на вопрос «С кем из класса вы хотели бы сидеть?», причем указать можно было, только одно имя. После, результаты опроса, я представил в виде графа. Учащиеся это вершины (34 вершины), ребра это желания учащихся сидеть с одноклассником, красным цветом выделены ребра, если предпочтения одноклассников совпали. 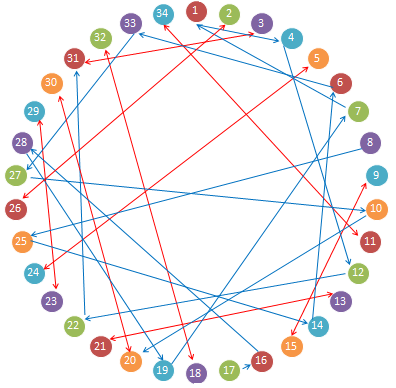 Тем самым можно сделать вывод, о том, что использование графов, может быть целесообразным не только при решении задач, но и в каких либо жизненных ситуациях, где необходимо наглядно продемонстрировать этот процесс или выстроить логическую цепочку. 7. Выводы Выполняя этот проект, я освоил основные понятия теории графов, изучил новые методы решения логических задач для школы, изучил элементы теории графов, узнал об использовании графов в науке и различных сферах жизни. Я пришел к выводу, что графы во многих отношениях облегчают нашу жизнь. Это касается не только их применения в школе, но и в реальной жизни. 8. Литературные источники Коннова Е.Г. Издательство «Легион-М» 2009 г. Энциклопедический словарь юного математика. Москва, Педагогика, 1985г. Засенок В.П. Графы в математике и в жизни/программа интеллектуального развития учащихся /выпуск 6./ Инновационно-образовательный центр-М. 1997года. Е.В. Галкин. Нестандартные задачи по математике. Задачи логического характера . Книга для учащихся 5-11 классов. “Просвещение” – “Учебная литература” Москва 1996. О.И.Мельников. Незнайка в стране графов. М.: КомКнига,2006. Л.Ю.Березина. Графы и их применение. Москва, «Просвещение», 1979 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
