проект. Проектная работа
 Скачать 99.55 Kb. Скачать 99.55 Kb.
|
|
Муниципальное бюджетное казачье общеобразовательное учреждение средняя общеобразовательная школа № 19 им. А.П.Васильева г. Курганинска ПРОЕКТНАЯ РАБОТА «Система счисления» Работу подготовил: Перевозчиков Денис Сергеевич учащийся 9 класса МБОУ СОШ№19 им. А.П. Васильева Руководитель: Ткаченко Сергей Николаевич г.Курганинск, 2022 Содержание
Введение На ранних ступенях развития общества люди почти не умели считать. Они отличали друг от друга совокупности двух и трех предметов; всякая совокупность, содержавшая большее число предметов, объединялась в понятии «много». Это был еще не счет, а лишь его зародыш. Впоследствии способность различать друг от друга небольшие совокупности развивалась; возникли слова для обозначений понятий «четыре», «пять», «шесть», «семь». Последнее слово длительное время обозначало также неопределенно большое количество. Наши пословицы сохранили память об этой эпохе («семь раз отмерь – один раз отрежь», «у семи нянек дитя без глазу», «семь бед – один ответ» и т.д.). Особо важную роль играл природный инструмент человека – его пальцы. Этот инструмент не мог длительно хранить результат счета, но зато всегда был «под рукой» и отличался большой подвижностью. Язык первобытного человека был беден; жесты возмещали недостаток слов, и числа, для которых еще не было названий, «показывались» на пальцах. Поэтому, вполне естественно, что вновь возникавшие названия «больших» чисел часто строились на основе числа 10 – по количеству пальцев на руках. На первых порах расширение запаса чисел происходило медленно. Сначала люди овладели счетом в пределах нескольких десятков и лишь позднее дошли до сотни. У многих народов число 40 долгое время было пределом счета и названием неопределенно большого количества. В русском языке слово «сороконожка» имеет смысл «многоножка»; выражение «сорок сороков» означало в старину число, превосходящее всякое воображение. На следующей ступени счет достигает нового предела: десяти десятков, и создается название для числа 100. Вместе с тем слово «сто» приобретает смысл неопределенно большого числа. Такой же смысл приобретают потом последовательно числа тысяча, десять тысяч (в старину это число называлось «тьма»), миллион. На современном этапе границы счета определены термином «бесконечность», который не обозначает какое-либо конкретное число. Современный человек в повседневной жизни постоянно сталкивается с числами и цифрами - они с нами везде. Различные системы счисления используются всегда, когда появляется потребность в числовых расчётах, начиная с вычислений учениками младших классов, выполняемых карандашом на бумаге, заканчивая вычислениями, выполняемыми на суперкомпьютерах. Поэтому эта тема для меня очень интересна, и мне захотелось узнать об этом больше. Цель изучение истории возникновения систем счисления, узнать принципы построения различных систем счисления и области их использования, классифицировать системы счисления получить необходимые навыки применения систем счисления в жизни. Гипотеза Человек использует только десятичную систему счисления, т.к. она удобна для счета, потому что у человека 10 пальцев. Основные задачи рассмотреть понятие систем счисления и их виды; изучить и проанализировать литературу, посвященную системам счисления; рассмотреть применение систем счисления в жизни человека и в компьютерной технике; разработать мини задачник по данной теме. 1.Теоретическая часть 1. 1 Виды системы счисления Все системы счисления делятся на позиционные и непозиционные. Непозиционная система счисления — это система, в которой количественный эквивалент каждой цифры не зависит от ее положения (места, позиции) в записи числа. Итак, в непозиционных системах счисления позиция, которую цифра занимает в записи числа, роли не играет. Так, например, римская система счисления непозиционная. В числах XI и IX "вес” обоих цифр одинаков, несмотря на их месторасположение. 1.2 Позиционные системы счисленияПозиционная система счисления — это система, в которой значение цифры зависит от ее места (позиции) в записи числа. Основание системы счисления количество знаков или символов, используемых для изображения числа в данной системе счисления. Основание системы счисления определяет её название: основание p - p-ая система счисления. Например, система счисления в основном, применяемая в современной математике, является позиционной десятичной системой, её основание равно десяти. Для записи любых чисел в ней используется десять всем хорошо известных цифр (0,1,2,3,4,5,6,7,8,9). Итак, мы сказали, что в позиционных системах счислениях имеет значение позиция, которую цифра занимает в записи числа. Так, запись 23 означает, что это число можно составить из 3 единиц и 2 десятков. Если мы поменяем позиции цифр, то получим совсем другое число – 32. Это число содержит 3 десятка и 2 единицы. «Вес» двойки уменьшился в десять раз, а «вес» тройки в десять раз возрос. 1.3 Развернутая запись числа Любое число N в позиционной системе счисления с основанием p может быть представлено в виде многочлена от p: N=ak pk + ak-1 pk-1+ak-2 pk-2+...+a1 p1+a0 p0+a-1 p-1+a-2 p-2+..., где N - число, p - основание системы счисления (p>1), ai - цифры числа (коэффициенты при степени p). Числа в p-ой системе счисления записываются в виде последовательности цифр: N=ak ak-1 ak-2 ...a1 a0 ,a-1 a-2... Запятая в последовательности отделяет целую часть числа от дробной. N=4567,1210=4*103+5*102+6*101+7*100+1*10-1+2*10-2 1.4 Двоичная система счисленияДля записи чисел используются только две цифры – 0 и 1. Выбор двоичной системы для использования в компьютере объясняется тем, что электронные элементы, из которых строятся ЭВМ, могут находиться только в двух хорошо различимых состояниях. По существу эти элементы представляют собой выключатели. Как известно выключатель либо включен, либо выключен. Третьего не дано. Одно из состояний обозначается цифрой 1, другое – 0. Благодаря таким особенностям двоичная система стала стандартом при построении ЭВМ. В этой системе счисления любое число может быть представлено в виде: N=ak 2k + ak-1 2k-1+ak-2 2k-2+...+a1 21+a0 20+a-1 2-1+a-2 2-2+.... Например:11001,012=1*24+1*23+0*22+0*21+1*20+0*2-1+1*2-2 (развернутая запись числа в двоичной системе счисления) 1.5 Восьмеричная система счисления
1.6 Шестнадцатеричная система счисленияДля обозначения цифр в шестнадцатеричной системе счисления используют десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и латинские буквы A(10), B(11), C(12), D(13), E(14), F(15). Эта система счисления, так же, как и восьмеричная
Развернутая запись числа в восьмеричной системе счисления: A2F,416=A*162+2*161+F*160+4*16-1 Перевод чисел в десятичную систему счисления.Алгоритм перевода Ap--A10.Представьте число в развернутой форме. Вычислите сумму ряда. Полученное число является значением числа в десятичной системе счисления.2416 = 2 * 161 + 4 * 160 = 32 + 4 = 361.7 Перевод в десятичную систему счисленияПо определению веса разряда pi = si, где i — номер разряда, а s — основание системы счисления. Тогда, обозначив цифры числа как ai, любое число, записанное в позиционной системе счисления, можем представить в виде: x = ansn + an-1sn-1 + ... + a2s2 + a1s1 + a0s0 + a-1s-1 + ... Например, для системы счисления с основанием 4: 1302.24 = 1⋅43 + 3⋅42 + 0⋅41 + 2⋅40 + 2⋅4-1 Выполнив вычисления, мы получим значение исходного числа, записанное в десятичной системе счисления (точнее, в той, в которой производим вычисления). В данном случае: 1302.24 = 1⋅43 + 3⋅42 + 0⋅41 + 2⋅40 + 2⋅4-1 = = 1⋅64 + 3⋅16 + 0⋅4 + 2⋅1 + 2⋅0,25 = = 64 + 48 + 2 + 0,5 = 114,5 Таким образом, для перевода числа из любой системы счисления в десятичную следует: пронумеровать разряды исходного числа; записать сумму, слагаемые которой получаются как произведения очередной цифры на основание системы счисления, возведенное в степень, равную номеру разряда; выполнить вычисления и записать полученный результат (указав основание новой системы счисления — 10). Примеры: 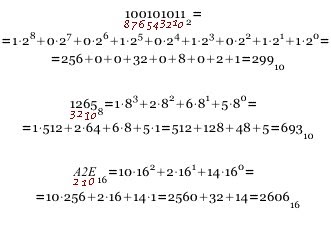 1.8 Перевод из десятичной системы счисленияВспомним пример перевода из системы счисления с основанием 4 в десятичную: 13024 = 1⋅43 + 3⋅42 + 0⋅41 + 2⋅40 = 114 Иначе это можно записать так: 114 = ((1 ⋅ 4 + 3) ⋅ 4 + 0) ⋅ 4 + 2 = 13024 Отсюда видно, что при делении 114 на 4 нацело в остатке должно остаться 2 — это младшая цифра при записи в четверичной системе. Частное же будет равно (1 ⋅ 4 + 3) ⋅ 4 + 0 Деление его на 4 даст остаток — следующую цифру (0) и частное 1 ⋅ 4 + 3. Продолжая действия, получим аналогичным образом и оставшиеся цифры. В общем случае для перевода целой части числа из десятичной системы счисления в систему с каким-либо другим основанием необходимо: Выполнить последовательное деление с остатком исходного числа и каждого полученного частного на основание новой системы счисления. Записать вычисленные остатки, начиная с последнего (т.е. в обратном порядке) Примеры: 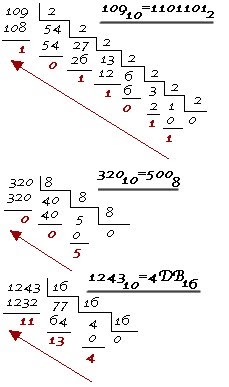 1.9 Системы счисления с кратными основаниямиПри работе с компьютерами широко применяют двоичную систему счисления (поскольку на ней основано представление информации в компьютере), а также восьмеричную и шестнадцатеричную, запись в которых более компактна и удобна для человека. С другой стороны, благодаря тому что 8 и 16 — степени 2, переход между записью в двоичной и одной из этих систем осуществляется без вычислений. Достаточно заменить каждый разряд шестнадцатеричной записи четырьмя (16=24) разрядами двоичной (и наоборот) по таблице. Примеры: 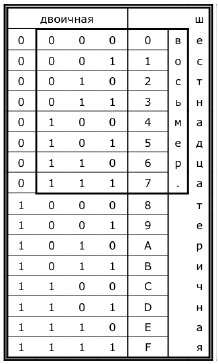 Аналогично происходит и перевод между двоичной и восьмеричной системой, только разряд восьмеричной соответствует трем разрядам двоичной (8=23) АрифметикаАрифметические операции в позиционной системе с любым основанием производятся по одним и тем же правилам: сложение, вычитание и умножение «в столбик», а деление — «уголком». Рассмотрим пример выполнения действий сложения и вычитания в двоичной, восьмеричной и шестнадцатеричной системах счисления. Сложение Двоичная система: В нулевом разряде: 1 + 0 = 0 В первом разряде: 1 + 1 = 2. 2 переносится в старший (2-й) разряд, обращаясь в единицу переноса. В первом разряде остается 2 - 2 = 0. Во втором разряде: 0 + 1 + 1 (перенос) = 2; Переносим в старший разряд, В третьем разряде: 1 + 1 + 1 (перенос) = 3; В старший разряд переносим 2, здесь остается 3 - 2 = 1. Продолжая вычисления, получим: 100110112 + 10011102 = 111010012 Восьмеричная система: Выполняем вычисления аналогично двоичной системе, но в старший разряд переносим 8. Получаем: 342618 + 44358 = 407168 Шестнадцатеричная система: A39116 + 853416 = 128C516 Вычитание Двоичная система: В нулевом разряде: 1 - 0 = 1 В первом разряде: 1 - 1 = 0. Во втором разряде: 0 - 1; необходимо занять единицу старшего разряда. Поскольку веса разрядов двоичной системы отличаются в 2 раза: 2 + 0 - 1 = 1 Из третьего разряда занимали единицу, там остался 0, поэтому вновь нужно занимать из старшего разряда. Продолжая вычисления, получим: 100110112 - 10011102 = 10011012 Восьмеричная система: Выполняем вычисления аналогично двоичной системе, но, занимая из старшего разряда, получаем 8. В результате: 342618 - 44358 = 276248 Шестнадцатеричная система: A39116 - 853416 = 1E3D16 1.10 Римская система счисления Непозиционная система счисления, в которой для записи чисел используются буквы латинского алфавита: 1 - I, 5 - V, 10 - X, 50 - L, 100 - C, 500 - D и 1000 - M. Для правильной записи больших чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц. Натуральные числа записываются при помощи повторения этих цифр. 2. История систем счисленияСистема счисления – это способ записи (изображения) чисел. Различные системы счисления, которые существовали раньше и которые используются в настоящее время, делятся на две группы: позиционные, непозиционные. Наиболее совершенными являются позиционные системы счисления. Они являются результатом длительного исторического развития непозиционных систем счисления. Цель создания системы счисления- выработка наиболее удобного способа записи количественной информации. Существует много различных систем счисления. Некоторые из них распространены, другие распространения не получили. Наиболее простая и понятная для нас система счисления - десятичная (основание 10). Понятна она потому, что мы используем ее в повседневной жизни. Единичная система В древние времена, когда люди начали считать, появилась потребность в записи чисел. Количество предметов, например, изображалось нанесением черточек или засечек на какой-либо твердой поверхности: камне, глине, дереве (до изобретения бумаги было еще очень далеко). Каждому предмету в такой записи соответствовала одна черточка. Археологами найдены такие «записи» при раскопках культурных слоев, относящихся к периоду палеолита (10–11 тысяч лет до н.э.). Ученые назвали этот способ записи чисел единичной (палочной) системой счисления. В ней для записи чисел применялся только один вид знаков – палочка. Каждое число в такой системе счисления обозначалось с помощью строки, составленной из палочек, количество которых равнялось обозначаемому числу. Неудобства такой системы записи чисел и ограниченность ее применения очевидны: чем большее число надо записать, тем длиннее строка из палочек; при записи большого числа легко ошибиться – нанести лишнее количество палочек или, наоборот, не дописать палочки. Можно предположить, что для облегчения счета люди стали группировать предметы по 3, 5, 10 штук. И при записи стали использовать знаки, соответствующие группе из нескольких предметов. Поскольку люди, при подсчете использовали пальцы рук, то первыми появились знаки для обозначения групп предметов из 5 и 10 штук (единиц). И таким образом возникли уже более удобные системы записи чисел. Древнегреческая нумерация В древнейшее время в Греции была распространена т.н. аттическая нумерация. Числа 1, 2, 3, 4 обозначались черточками , ,,. Число 5 записывалось знаком (древнее начертание буквы «пи», с которой начинается слово «пенте» – пять); числа 6, 7, 8, 9 обозначались , , , . Число 10 обозначалось (начальной буквой слова «дека» – десять). Числа 100, 1000 и 10000 обозначались , , . Числа 50, 500, 5000 обозначались комбинациями знаков 5 и 10, 5 и 100, 5 и 1000. В третьем веке до н.э. аттическая нумерация была вытеснена так называемой ионийской системой. В ней числа 1 – 9 обозначались первыми девятью буквами алфавита; числа 10, 20, 30, … , 90 – следующими девятью буквами; числа 100, 200, … , 900 – последними девятью буквами. Обозначение чисел в ионийской системе нумерации Южные и восточные славянские народы для записи чисел пользовались алфавитной нумерацией. У одних славянских народов числовые значения букв установились в порядке славянского алфавита, у других же (в том числе у русских) роль цифр играли не все буквы, а только те, которые имеются в греческом алфавите. Над буквой, обозначавшей цифру, ставился специальный значок: («титло»). Обозначение чисел в древнеславянской системе нумерации Славянская нумерация В России славянская нумерация сохранилась до конца XVII века. При Петре I возобладала так называемая «арабская нумерация», которой мы пользуемся и сейчас. Славянская нумерация сохранялась только в богослужебных книгах. При записи чисел, больших 10, цифры писались слева направо в порядке убывания десятичных разрядов (однако иногда для чисел от 11 до 19 единицы записывались ранее десяти). Для обозначения тысяч перед числом их (слева внизу) ставился особый знак . Римская нумерация Древние римляне пользовались нумерацией, которая сохраняется до настоящего времени под именем «римской нумерации». Мы пользуемся ей для обозначения веков, юбилейных дат, наименования съездов и конференций, для нумерации глав книги или строф стихотворения. В позднейшем своем виде римские цифры выглядят так: , , , , , , . В римской нумерации явственно сказываются следы пятиричной системы счисления. В языке же римлян (латинском) никаких следов пятиричной системы нет. Значит, эти цифры были заимствованы римлянами у другого народа (предположительно у этрусков). Все целые числа (до 5000) записываются с помощью повторения вышеприведенных цифр. При этом, если большая цифра стоит перед меньшей, то они складываются, если же меньшая стоит перед большей (в этом случае она не может повторяться), то меньшая вычитается из большей. Подряд одна и та же цифра ставится не более трех раз. Выполнение арифметических действий над многозначными числами в этой записи очень громоздко и трудно. Тем не менее, римская нумерация преобладала в Италии до XIII века, а в других странах Западной Европы - до XVI века. Вавилонская поместная нумерация В древнем Вавилоне примерно за 40 веков до нашего времени создалась поместная (позиционная) нумерация, т.е. такой способ изображения чисел, при котором одна и та же цифра может обозначать разные числа, смотря по месту, занимаемому этой цифрой. Наша теперешняя нумерация - тоже поместная, однако в вавилонской поместной нумерации ту роль, которую играет у нас число 10, играло число 60, и потому эту нумерацию называют шестидесятеричной. Числа, меньшие 60, обозначались с помощью двух знаков: для единицы и для десятка . Они имели клинообразный вид, так как вавилоняне писали на глиняных дощечках палочками треугольной формы. Эти знаки повторялись нужное число раз. При отсутствии промежуточного разряда применялся знак. Шестидесятеричная запись целых чисел не получила распространения за пределами ассиро-вавилонского царства, но шестидесятеричные дроби проникли далеко за эти пределы: в страны Среднего Востока, Средней Азии, в Северную Африку и Западную Европу. Они широко применялись, особенно в астрономии, вплоть до изобретения десятичных дробей. Следы шестидесятеричных дробей сохраняются и поныне в делении углового и дугового градуса (а также часа) на 60 минут и минуты на 60 секунд. Заключение Интуитивное представление о числе, так же старо, как и само человечество. Прежде чем человек научился считать или придумал слова для обозначения чисел, он, несомненно, владел наглядным, интуитивным представлением о числе, позволявшим ему различать одного человека и двух людей или двух и многих людей. Счет изначально был связан с вполне конкретным набором объектов, и самые первые названия чисел были прилагательными. Высшим достижением древней арифметики является открытие позиционного принципа представления чисел. Хорошо известно, что первой из известных систем счисления, основанных на позиционном принципе, была вавилонская 60-ричная система счисления, возникшая в Древнем Вавилоне примерно во 2-м тысячелетии до новой эры. Мы используем для повседневных вычислений десятичную систему счисления. Хорошо известно, что предшественницей десятичной системы счисления является Индусская десятичная система, возникшая примерно в 8-м столетии нашей эры. Известный французский математик Лаплас (1749-1827) выразил свое восхищение позиционным принципом и десятичной системой в следующих словах: "Мысль выражать все числа 9 знаками, придавая им, кроме значения по форме, еще значение по месту, настолько проста, что именно из-за этой простоты трудно понять, насколько она удивительна. Как нелегко было прийти к этой методе, мы видим на примере величайших гениев греческой учености Архимеда и Аполлония, от которых эта мысль осталась скрытой". Леонардо Пизанский (Фибоначчи) в своем сочинении "Liber abaci" (1202) выступил убежденным сторонником новой нумерации. Он писал: "Девять индусских знаков - суть следующие: 9, 8, 7, 6, 5, 4, 3, 2, 1. С помощью этих знаков и знака 0, который называется по-арабски "zephirum", можно написать какое угодно число". Современные компьютеры основываются на "двоичной" системе счисления. Нужно признать важность не только самой распространенной системы, которой мы пользуемся ежедневно. Но и каждой по отдельности. Ведь в разных областях используются разные системы счисления, со своими особенностями и характерными свойствами. Список использованной литературы https://nsportal.ru/ap/library/nauchno-tekhnicheskoe-tvorchestvo/2012/08/22/referat-i-prezentatsiya-na-temu-sistemy https://multiurok.ru/files/proekt-po-informatike-sistema-schisleniia.html http://qwertylike35.blogspot.com/p/blog-page_3567.html https://multiurok.ru/files/proekt-po-informatike-sistema-schisleniia.html https://www.sites.google.com/site/415ict/textbooks/numbers |
