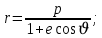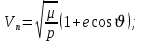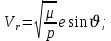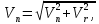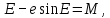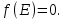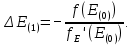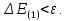Прогнозирование невозмущенного движения космического аппарата в центральном поле притяжения Земли. Баллистика ЛР2. Прогнозирование невозмущенного движения космического аппарата в центральном поле притяжения Земли
 Скачать 1.09 Mb. Скачать 1.09 Mb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное автономное образовательное учреждение высшего образования «Самарский национальный исследовательский университет имени академика С.П. Королева» (Самарский университет) Институт авиационной и ракетно-космической техники Кафедра динамики полёта и систем управления Дисциплина «Баллистика ракет» Отчёт ПО ЛАБОРАТОРНОЙ РАБОТЕ № 2 по теме «Прогнозирование невозмущенного движения космического аппарата в центральном поле притяжения Земли» Самара 2022 ЗАДАНИЕ Спрогнозировать движение КА по эллиптической орбите для ряда последовательных моментов времени 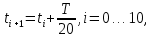 где где  – период обращения КА по орбите, a – большая полуось орбиты. – период обращения КА по орбите, a – большая полуось орбиты.Определить положение КА на траектории, то есть найти угол истинной аномалии 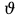 , расстояние r от центра Земли, трансверсальную , расстояние r от центра Земли, трансверсальную  и радиальную и радиальную  составляющие скорости, модуль скорости V и построение зависимостей данных параметров движения от времени. составляющие скорости, модуль скорости V и построение зависимостей данных параметров движения от времени.Проверить результаты работы путём самостоятельного приближённого решения трансцендентного уравнения. Исходные данные: 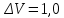 км/с – приращение скорости; км/с – приращение скорости; км – высота начальной круговой орбиты. км – высота начальной круговой орбиты.Характеристики Земли: 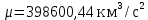 – гравитационный параметр; – гравитационный параметр;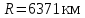 – средний радиус. – средний радиус.РЕФЕРАТ Отчёт 19 с, 8 рисунков, 1 таблица, 1 приложение. КОСМИЧЕСКИЙ АППАРАТ, ЭЛЛИПТИЧЕСКАЯ ТРАЕКТОРИЯ, СКОРОСТЬ, ТРАНСЦЕНДЕНТНОЕ УРАВНЕНИЕ, МЕТОД НЬЮТОНА. Цель работы: углублённое изучение вопросов движения КА в центральном поле притяжения планеты, развитие навыков решения с помощью ЭВМ задач динамики и теории полёта, приводящихся к многократному отысканию корней трансцендентных уравнений. СОДЕРЖАНИЕВВЕДЕНИЕВ данной работе кратко описывается физическая и математическая постановка задачи при движении КА по эллиптической траектории. Приводятся уравнение Кеплера, формулы для расчёта угла истинной аномалии 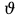 , расстояния r от центра Земли, трансверсальной , расстояния r от центра Земли, трансверсальной  и радиальной и радиальной  составляющих скорости, модуля скорости V и строятся зависимости данных параметров движения от времени. Даётся описание метода Ньютона для решения трансцендентного уравнения Кеплера, приводится графическая иллюстрация метода. составляющих скорости, модуля скорости V и строятся зависимости данных параметров движения от времени. Даётся описание метода Ньютона для решения трансцендентного уравнения Кеплера, приводится графическая иллюстрация метода.1 Постановка задачиКосмический аппарат стартует с круговой орбиты вокруг Земли высотой 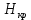 . Время работы разгонного двигателя не учитывается, и полагается, что круговая скорость КА . Время работы разгонного двигателя не учитывается, и полагается, что круговая скорость КА 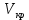 , км/с, изменяется мгновенно на величину , км/с, изменяется мгновенно на величину 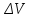 . . Рассматривается движение КА, как материальной точки, в центральном поле притяжения Земли без учёта возмущающих воздействий. В соответствии с законами механики полёта траектория при сделанных допущениях является дугой конического сечения, причём перигей орбиты полёта совпадает с точкой старта. В рассматриваемой задаче имеет место эллиптическая траектория, поэтому скорости КА определяются следующим соотношениям:
где  – параболическая скорость на высоте – параболическая скорость на высоте 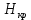 . .Необходимо сделать прогноз движения КА: для ряда последовательных моментов времени  определить положение КА на траектории, то есть найти угол истинной аномалии определить положение КА на траектории, то есть найти угол истинной аномалии 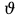 , расстояние rот центра Земли, трансверсальную , расстояние rот центра Земли, трансверсальную  и радиальную и радиальную  составляющие скорости, модуль скорости V(рисунок 1.1). составляющие скорости, модуль скорости V(рисунок 1.1).На практике эта информация необходима для решения задач, связанных с управлением полётом и наблюдением за КА. Если найден угол истинной аномалии, то искомые параметры r, V,  , ,  определяются следующими соотношениями: определяются следующими соотношениями:
где 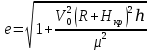 – эксцентриситет орбиты; – эксцентриситет орбиты; 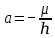 – большая полуось орбиты, км; – большая полуось орбиты, км;  – фокальный параметр орбиты, км; – фокальный параметр орбиты, км;  – постоянная интеграла энергии, – постоянная интеграла энергии,  Для определения угла 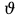 необходимо решить трансцендентное уравнение Кеплера: необходимо решить трансцендентное уравнение Кеплера:
где 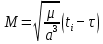 – угол среднего движения по эллиптической траектории, рад ( – угол среднего движения по эллиптической траектории, рад (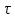 – момент времени прохождения через перицентр, с); E – угол эксцентричной аномалии, рад. – момент времени прохождения через перицентр, с); E – угол эксцентричной аномалии, рад.
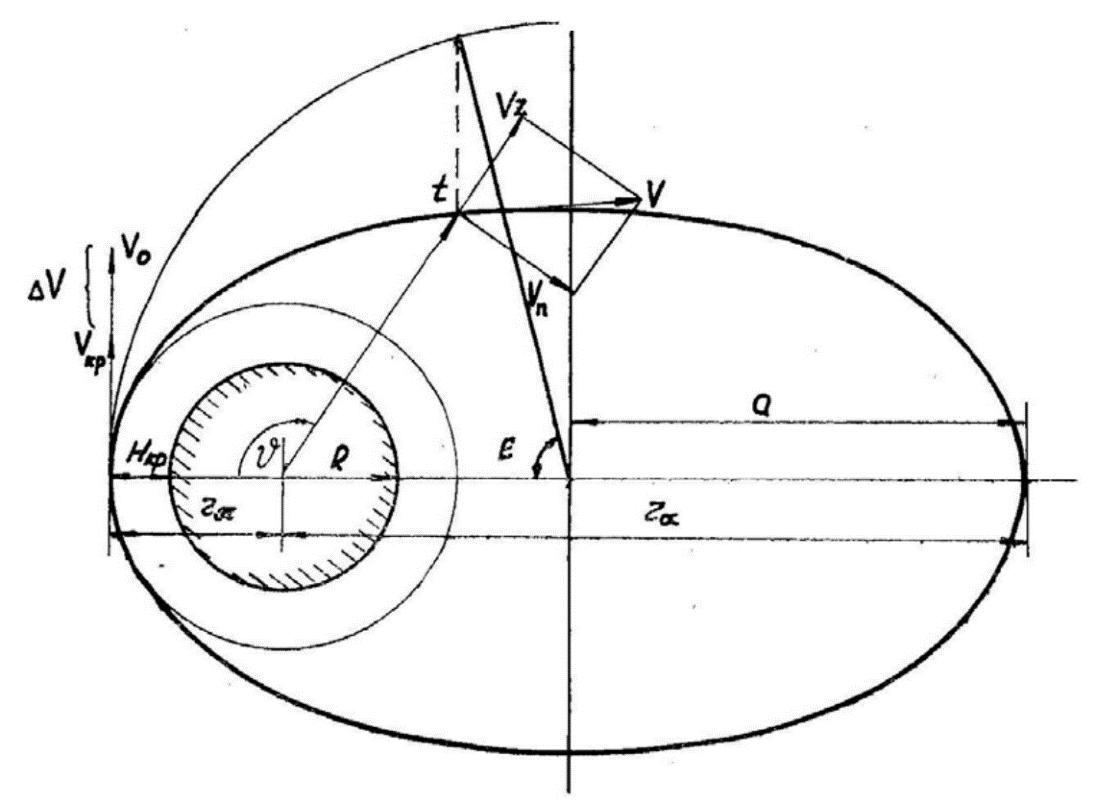 Рисунок 1.1 – Движение КА по эллиптической орбите 2 Метод решенияОсновой решения сформулированной задачи является многократное решение трансцендентного уравнения, которое выполняется приближённо одним из методов вычислительной математики. Уравнение (1.6) можно преобразовать к виду
Для решения трансцендентного уравнения применим метод Ньютона. Он относится к классу методов последовательных приближений и требует вычисления первой производной  . .Алгоритм метода Ньютона имеет следующий вид: 1) Выбор начального приближения 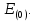 2) Вычисление  и и  в точке начального приближения в точке начального приближения 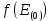 , , 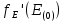 . .3) Вычисление первого приращения аргумента E:
4) Вычисление первого приближения корня по формуле:
5) Анализ выполнения критерия прекращения расчётов
Если условие (2.4) выполняется, то считается, что найдено решение уравнения (2.1) с заданной точностью  . .Геометрическая интерпретация метода представлена на рисунке 2.1. 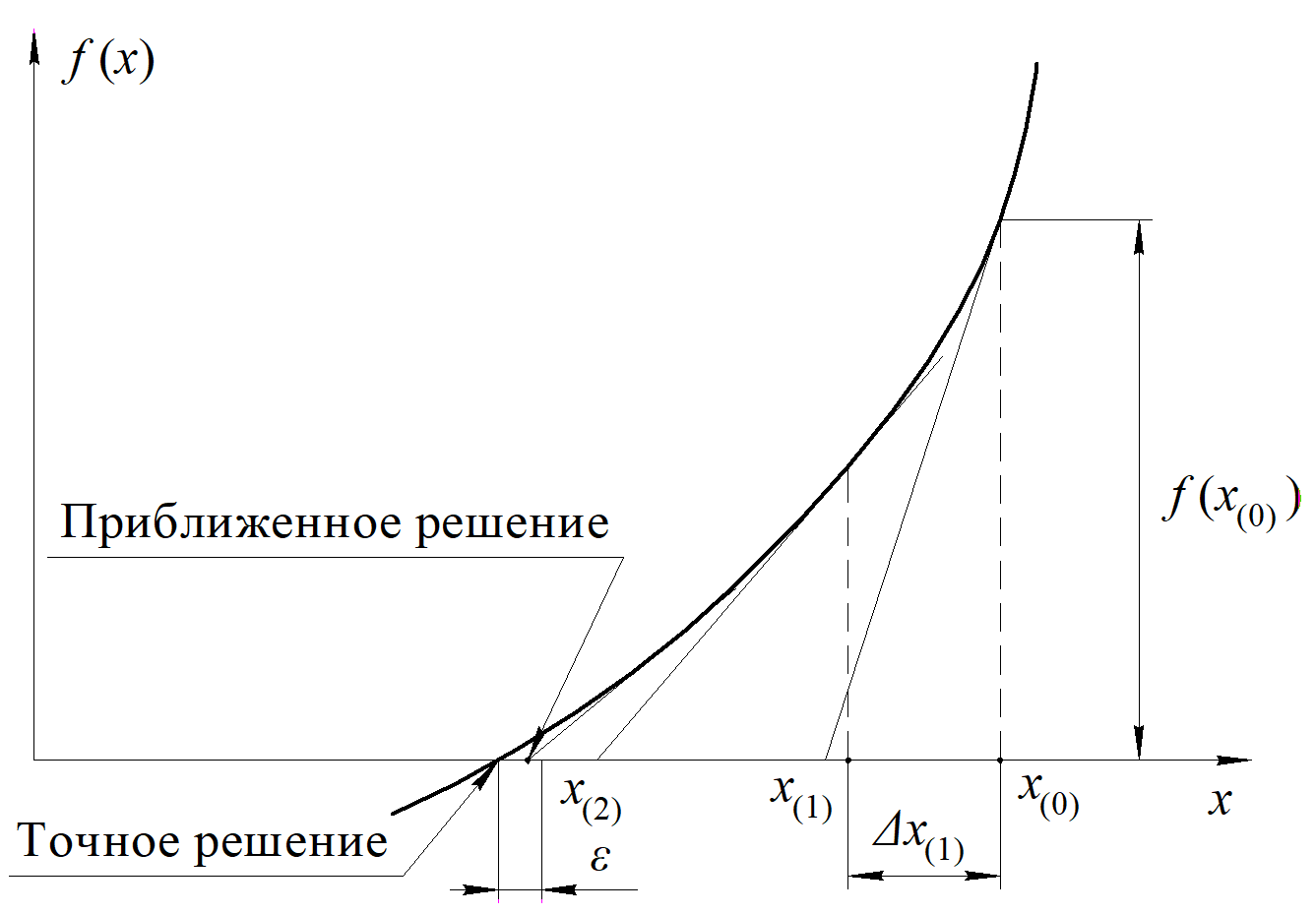 Рисунок 2.1 – Графическая иллюстрация решения уравнений методом Ньютона 3 Выполнение расчётов на ЭВМ и анализ результатовПостроение графиков 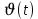 , r(t), , r(t), 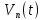 , , 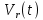 и V(t) при заданных исходных данных, изображённых на рисунках 3.1-3.5, выполнено с использованием возможностей программы Prognoz. Числовые значения расчётов приведены в приложении. и V(t) при заданных исходных данных, изображённых на рисунках 3.1-3.5, выполнено с использованием возможностей программы Prognoz. Числовые значения расчётов приведены в приложении.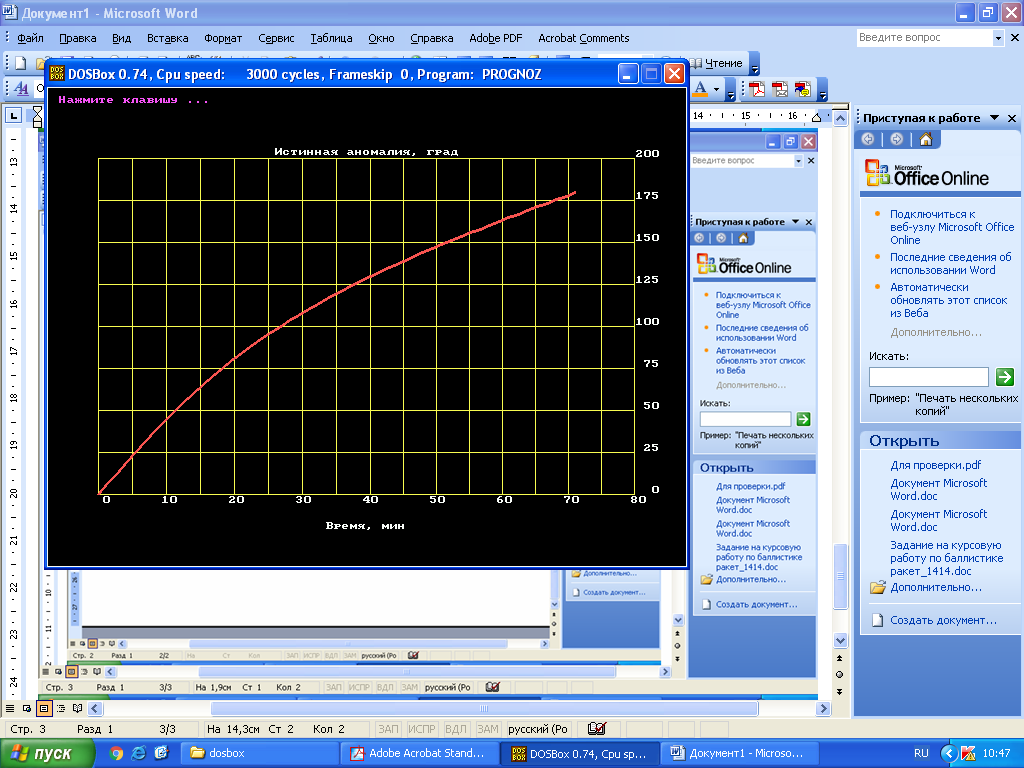 Рисунок 3.1 – Зависимость угла истинной аномалии от времени  Рисунок 3.2 – Зависимость расстояния от центра Земли от времени  Рисунок 3.3 – Зависимость трансверсальной скорости от времени  Рисунок 3.4 – Зависимость радиальной скорости от времени 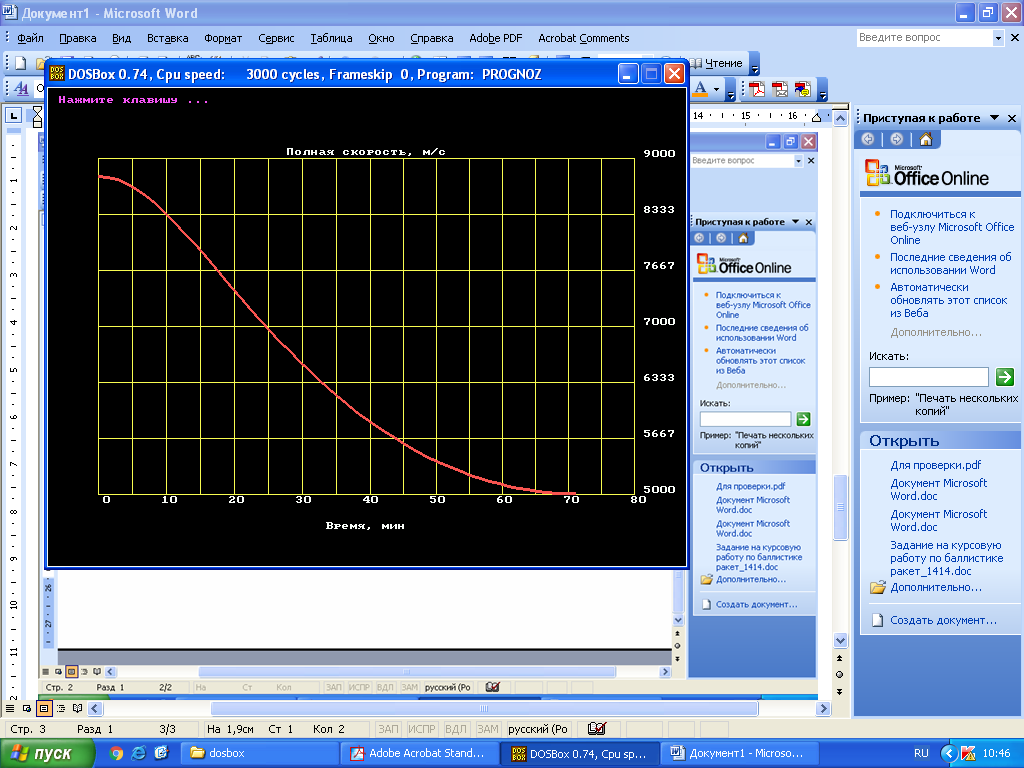 Рисунок 3.4 – Зависимость модуля скорости от времени Из построенных графиков видно, что в точке, соответствующей значению угла истинной аномалии = 0, находится перигей орбиты, а в точке = - апогей орбиты. В данных точках отсутствует радиальная составляющая скорости, но она быстро нарастает при удалении от перигея, а, пройдя примерно четверть расстояния до апогея, начинает уменьшаться. Трансверсальная составляющая скорости отлична от нуля и имеет наибольшее значение в точке перигея орбиты, что аналогично величине полной скорости КА. 4 Решение трансцендентного уравнения методом НьютонаДля решения уравнения (1.6) в момент времени  используются возможности программы Microsoft Excel. используются возможности программы Microsoft Excel.Сначала приведём уравнение (1.6) к виду (2.1) и определим его первую производную по E:   В качестве начального приближения принимаем  Теперь необходимо рассчитать все необходимые для решения параметры. 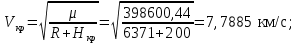  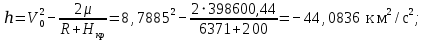 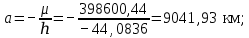 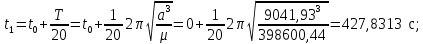  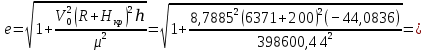  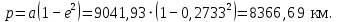 Теперь, используя значения найденных параметров, можно решить уравнение Кеплера в заданный момент времени с помощью численного метода. На рисунке 4.1 представлен график зависимости  . Результаты трёх итераций метода Ньютона представлены в таблице 4.1 и они совпадают с аналогичным расчётом программы Prognoz, который приведён в приложении. . Результаты трёх итераций метода Ньютона представлены в таблице 4.1 и они совпадают с аналогичным расчётом программы Prognoz, который приведён в приложении. Рисунок 4.1 – График зависимости  Таблица 4.1 – Решение трансцендентного уравнения
Вычислим вручную необходимые параметры движения в заданный момент времени с учётом найденного значения угла истинной аномалии 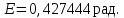  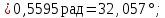 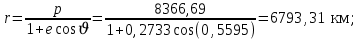 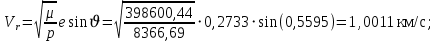   Все рассчитанные величины совпадают с расчётом программы Prognoz. ЗАКЛЮЧЕНИЕВ результате выполнения работы была изучена постановка задачи о прогнозировании невозмущенного движения КА в центральном поле притяжения планеты. Изучены основные параметры движения КА по эллиптической орбите. Построены и проанализированы графики зависимостей этих параметров от времени. Подробно рассмотрен и применён на практике метод Ньютона для численного решения нелинейных уравнений. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ1 Белоконов, В.М. Прогнозирование невозмущенного движения космического аппарата в центральном поле притяжения Земли [текст]/ В.М. Белоконов, И.В. Белоконов. Тип. УЭЗ КуАИ, 1984. - 15 с. ПРИЛОЖЕНИЕРезультаты расчётов в программе Prognoz 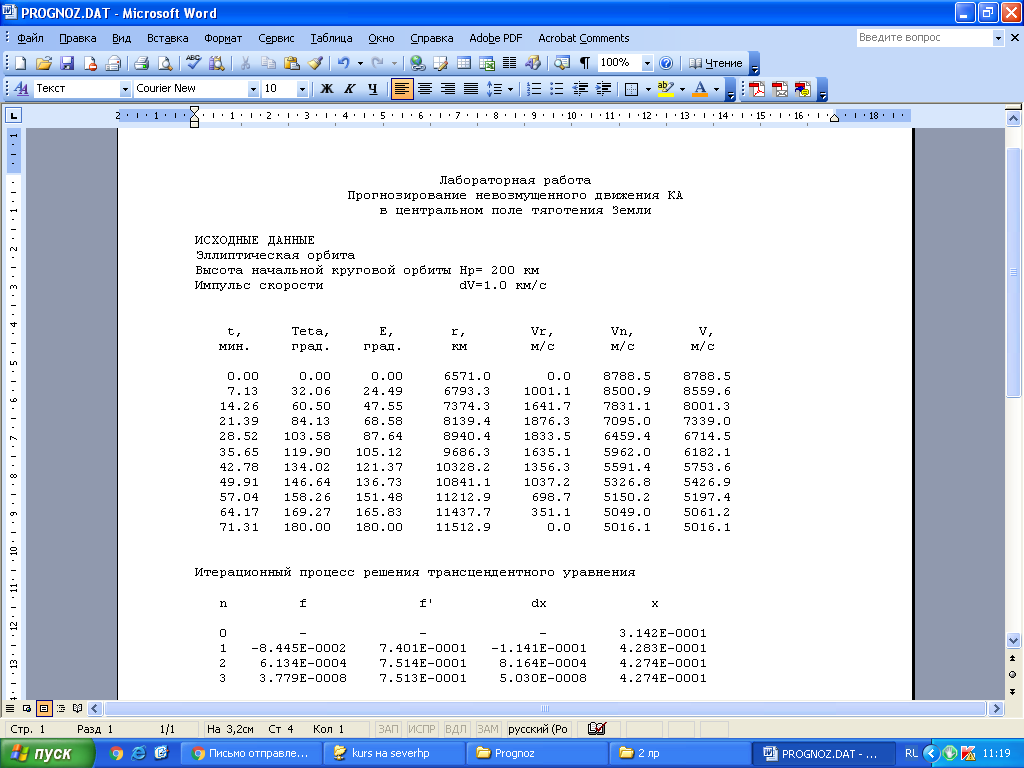 |