учебник по паскалю. Программа 5 Алгоритм 5 Свойства алгоритма 6 Формы записи алгоритма 6

• Название: Программа 5 Алгоритм 5 Свойства алгоритма 6 Формы записи алгоритма 6
• Анкор: учебник по паскалю.doc
• Дата: 03.02.2017
• Размер: 2.21 Mb.
• Имя файла: учебник по паскалю.doc
• Тип: Программа; #1964
• страница: 17 из 35

17. Матрицы и типовые алгоритмы обработки матриц

Многие задачи связаны с обработкой многомерных массивов данных. Наиболее распространены при этом двумерные массивы.

В математике двумерные массивы представляются матрицей: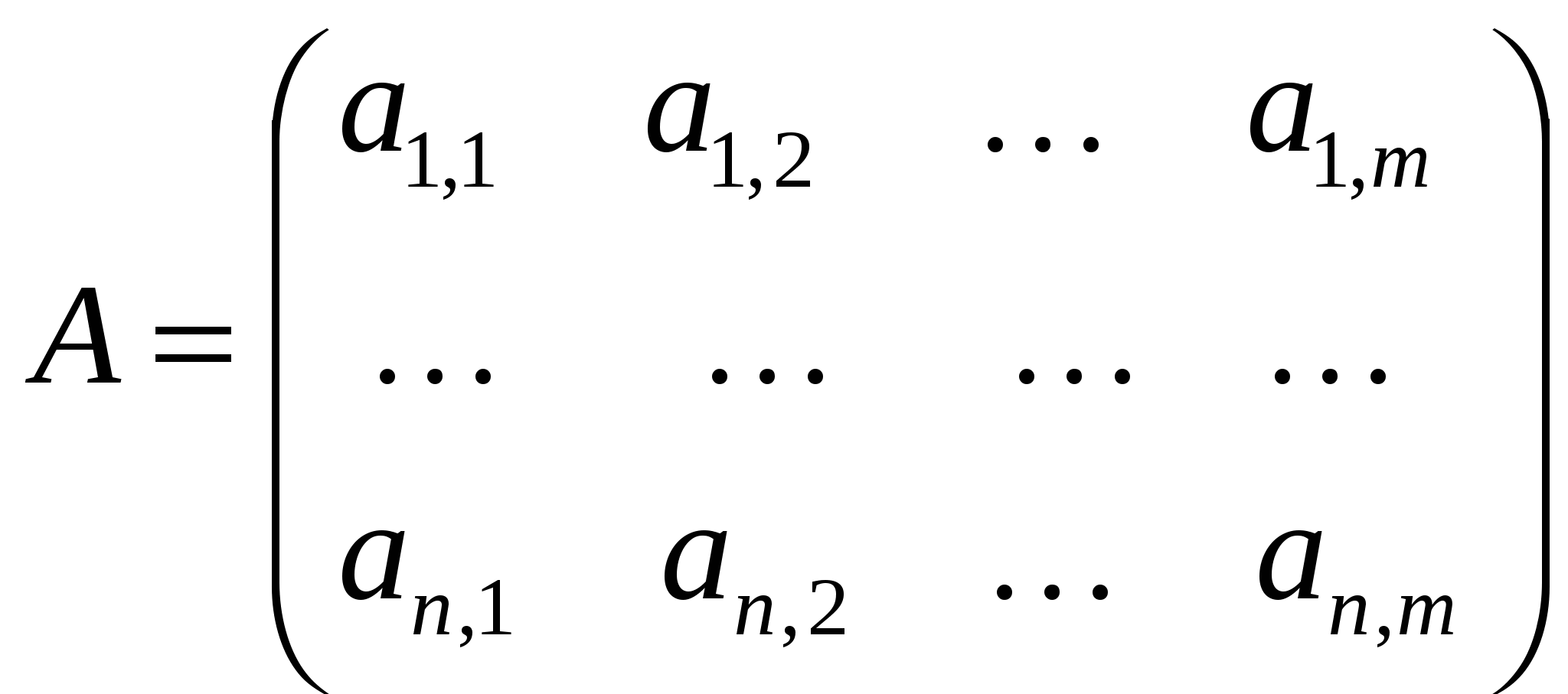



или, в сокращенной записи,

,

где n -- число строк матрицы, m -- число столбцов, i, j -- индексы (номера) текущих строки и столбца, на пересечении которых находится элемент .

Как и другие объекты данных, матрица описывается в разделе var. От вектора ее описание отличается тем, что в квадратных скобках перечисляются два оператора диапазона, указывающие, соответственно, нумерацию строк и столбцов матрицы:

var ИмяМатрицы: array

[n1..n2, m1..m2] of Тип;

Здесь n1..n2 -- диапазон значений номера строки, n1 и n2 -- целочисленные константы, m1..m2 -- диапазон значений номера столбца, значения m1 и m2 также целочисленные.

Как и векторы, матрицы могут быть образованы из элементов любого существующего в языке типа данных.

Под матрицу из n строк и m столбцов выделяется область памяти размером n*m*k байт, где k -- размер в байтах одного элемента. Для известных нам типов данных этот размер можно узнать из табл. 2.1. В оперативной памяти матрица хранится всегда построчно.

Например, для матрицы A, описанной оператором вида

var A:array [1..5,1..4] of real;

выделяется 20 ячеек памяти по 6 байт, причем в следующей за элементом A_1,4 ячейке хранится значение элемента A_2,1.

Обращение к отдельным элементам матрицы осуществляется с помощью переменной с двумя индексами, например:

a_i,j a[i,j]

a_2,1 a[2,1]

a_2n,k a[2*n,k]

Первый индекс, как и в математике, всегда показывает номер строки, а второй -- номер столбца.

Поскольку адресация памяти в любом случае линейна, следует понимать матрицу как удобный для программиста структурный тип данных. В отдельных случаях использование матрицы может быть заменено использованием вектора с тем же количеством элементов: так, матрице A_n,m всегда может быть сопоставлен вектор b из n*m элементов, а обращение к элементу A[i,j] при нумерации строк и столбцов с единицы может быть заменено на обращение к элементу b[(i-1)*m+j].

Подобно тому, как любая последовательная обработка вектора выполняется в цикле for, обработка матрицы осуществляется в двойном цикле for:

for i:=1 to n do

for j:=1 to m do

{Обработка элемента A[i,j]}

Согласно правилу выполнения кратных циклов, переменная j меняется в этом двойном цикле быстрее, чем i, таким образом, обработка всех элементов матрицы будет выполнена построчно. Для последовательной обработки всех элементов матрицы по столбцам достаточно поменять местами циклы по i и j:

for j:=1 to m do

for i:=1 to n do

{Обработка элемента A[i,j]}

Теоретически мы могли бы решить эту же задачу и перестановкой индексов в обращении к элементу матрицы (использовать запись A[j,i] вместо A[i,j]), однако, во избежание путаницы, делать этого не рекомендуется.

Приведем примеры использования двойного цикла for для ввода и вывода элементов матрицы. Пусть матрица c размерностью 42 (как мы помним, это означает, что в матрице 4 строки и 2 столбца) описана оператором вида

var c:array [1..4,1..2] of real;

В программе предусмотрено также 2 целочисленных счетчика для строк и столбцов матрицы:

var i,j:integer;

В этом случае типовой ввод матрицы с клавиатуры мог бы выглядеть так:

writeln ('Введите матрицу c ',

'размерностью 4*2');

for i:=1 to 4 do

for j:=1 to 2 do read (c[i,j]);

Иногда удобнее печатать отдельное приглашение к вводу каждого элемента:

writeln ('Введите матрицу c[4,2]');

for i:=1 to 4 do

for j:=1 to 2 do begin

write ('c[',i,',',j,']=');

readln (c[i,j]);

end;

Например, в качестве приглашения к вводу элемента c_1,1 на экране будет напечатано:

c[1,1]=

Оператор readln используется, поскольку элементы вводятся по одному.

Как и для векторов, возможны альтернативные способы ввода -- описание матрицы в разделе констант и формирование ее элементов из случайных чисел. Приведем пример описания матрицы констант размерностью 23:

const d:array [1..2,1..3] of integer=(

(1,2,3),

(4,5,6)

);

Как видно из примера, для описания матрицы констант создается список ее строк, каждая строка, в свою очередь, представляет собой список значений элементов.

Вывод на экран матрицы небольшой размерности бывает удобно реализовать в виде "одна строка матрицы на одной строке экрана". Для этого элементы матрицы во внутреннем цикле печатаются оператором write, не переводящим строку на экране, а во внешнем цикле выполняется writeln:

writeln ('Матрица c:');

for i:=1 to 4 do begin

writeln;

for j:=1 to 2 do write (c[i,j]:4:1);

end;

Разумеется, при выводе элементов матрицы можно использовать константы ширины и точности.

Базовые алгоритмы обработки матриц -- те же, что мы изучили в гл. 11-15. Отличие состоит в том, что реализацию этих алгоритмов можно условно рассматривать для двух типов задач:

• 
  алгоритмы реализуются при обработке всех элементов матрицы;
  
• 
  алгоритмы реализуются при обработке отдельных строк или столбцов матрицы.
  

В первом случае типовая учебная задача на матрицу отличается от аналогичной задачи с вектором лишь тем, что используются двойные циклы ввода, обработки и вывода.

1. Приведем пример реализации алгоритма первого типа.

В матрице A размерностью 4*4 найти сумму ее положительных элементов, произведение элементов, значения которых попадают в интервал [2, 10], а также отношение этих двух величин.

var a:array [1..4,1..4] of real;

i,j:integer;

s,p,z:real;

begin

{Цикл ввода}

writeln ('Ввод матрицы размерностью 4*4');

for i:=1 to 4 do

for j:=1 to 4 do read (a[i,j]);

{Начальные значения и цикл обработки}

s:=0;

p:=1;

for i:=1 to 4 do

for j:=1 to 4 do begin

if a[i,j]>0 then s:=s+a[i,j];

if (a[i,j]>=2) and (a[i,j]<=10)

then p:=p*a[i,j];

end;

{Вывод результатов}

writeln ('Сумма=',s:6:2);

writeln ('Произведение=',p:6:2);

if p<>0 then begin

z:=s/p;

writeln ('Отношение=',z:6:2);

end

else writeln ('p=0, отношение ',

'вычислить нельзя');

reset (input); readln;

end.

Поскольку о типе матрицы в условии задачи ничего не сказано, выбран "более общий" тип real. Способ ввода также выбран "по умолчанию" -- пользователь вводит значения элементов матрицы с клавиатуры. Искомые сумма, произведение и отношение обозначены, соответственно, s, p и z.

2. Рассмотрим пример реализации алгоритма второго типа. Отличие его в том, что алгоритм подсчета или поиска каждый раз заново реализуется во внутреннем цикле, таким образом, искомая в двойном цикле величина заново получает значение на каждом шаге внешнего цикла.

Задана матрица C размерностью 34. Найти номер строки, сумма элементов которой максимальна.

На этот раз заполним матрицу случайными числами. Обозначим s сумму элементов очередной строки, max -- максимальную из этих сумм. В качестве искомого номера строки введем целочисленную переменную imax, в которую будем заносить номер текущей строки i, если для этой строки выполняется соотношение s>max. Переменную s следует инициализировать на каждом шаге внешнего цикла по i (ведь сумма элементов ищется заново в каждой строке), тогда как переменная max ищется для всей матрицы и инициализируется один раз до двойного цикла:

var c:array [1..3,1..4] of real;

i,j,imax:integer;

s,max:real;

begin

{Формирование матрицы с ее выводом}

writeln;

write ('Матрица C');

for i:=1 to 3 do begin

writeln;

for j:=1 to 4 do begin

c[i,j]:=random*10

{вещественные числа от 0 до 10};

write (c[i,j]:6:2);

end;

end;

{Поиск номера строки и вывод результата}

max:=-1e30;

for i:=1 to 3 do begin

s:=0;

for j:=1 to 4 do s:=s+c[i,j];

if s>max then begin

max:=s;

imax:=i;

end;

end;

writeln;

writeln ('Номер строки=',imax);

end.

Аналогично могут быть реализованы типовые алгоритмы в столбце матрицы -- как описано выше, для этого достаточно поменять местами циклы по i и j.

3. Встречаются также задачи, где результаты обработки строк или столбцов матрицы должны быть занесены в вектор. Решим задачу подобного типа.

В матрице S размерностью 204 приведены оценки 20 студентов за 4 экзамена последней сессии. Подчитать и вывести на экран элементы вектора, содержащего средние баллы каждого студента.

Обозначим искомый вектор как B. Его размерность очевидна, поскольку каждый элемент вектора зависит от одной строки матрицы. Применив алгоритм обработки строк матрицы, получаем следующую программу:

var s:array [1..20,1..4] of integer;

b:array [1..20] of real;

i,j:integer;

begin

{Матрица s из случайных оценок от 3 до 5}

for i:=1 to 20 do

for j:=1 to 4 do s[i,j]:=3+random(3);

{Обрабатываем матрицу построчно,

формируя вектор B}

for i:=1 to 20 do begin

b[i]:=0;

for j:=1 to 4 do b[i]:=b[i]+s[i,j];

b[i]:=b[i]/4;

end;

{Выводим оценки со средними баллами}

writeln;

write ('Оценки':8,' Баллы');

for i:=1 to 20 do begin

writeln;

for j:=1 to 4 do write (s[i,j]:2);

write (b[i]:5:2);

end;

end.

4. Нередко встречаются задачи, требующие обработки элементов, расположенных под или над главной диагональю матрицы. Главная диагональ характеризуется тем, что номера строк и столбцов расположенных на ней элементов совпадают. Корректно это понятие определено только для квадратных матриц с одинаковым числом строк и столбцов. Соответственно, для обработки элементов, лежащих на главной диагонали матрицы A размерностью nn было бы достаточно цикла

for i:=1 to n do begin

{Обработка элемента A[i,i]}

end;

Когда требуется обработать элементы, лежащие под главной диагональю (для них номер строки больше номера столбца), двойной цикл обработки мог бы выглядеть так:

for i:=1 to n do

for j:=1 to n do begin

if i>j then begin

{Обработка элемента A[i,j]}

end;

end;

Приведенный код имеет тот недостаток, что в нем выполняются заведомо лишние шаги цикла. Действительно, для квадратной матрицы размерностью nn мы выполняем n² шагов двойного цикла, тогда как имеется всего элементов под главной диагональю. Исправить ситуацию может двойной цикл с переменной границей, подобный изученному выше:

for i:=1 to n do

for j:=1 to i-1 do begin

{Обработка элемента A[i,j]}

end;

Этот цикл выполняется ровно раз. Для обработки только элементов, лежащих над главной диагональю, этот цикл будет выглядеть следующим образом:

for i:=1 to n do

for j:=i+1 to n do begin

{Обработка элемента A[i,j]}

end;

5. Распространенный класс задач, связанных с умножением и обращением матриц, мы рассмотрим в гл. 18. Сейчас же ограничимся реализацией хорошо известного алгоритма умножения матрицы A размерностью nm на вектор b размерности m. Напомним, что в результате умножения получается вектор размерности n (обозначим его c), а само умножение состоит в том, что каждая строка матрицы скалярно умножается на вектор по формуле и результат заносится в компоненту c_i. Применив известные нам типовые алгоритмы, напишем следующую программу:

const n=3; m=4;

{размерности матрицы и векторов}

var a:array [1..n,1..m] of real;

b:array [1..m] of real;

c:array [1..n] of real;

i,j:integer;

begin

{Формируем матрицу A из случайных чисел}

writeln ('Матрица A');

for i:=1 to n do begin

for j:=1 to m do begin

a[i,j]:=random*10;

write (a[i,j]:6:2);

end;

writeln;

end;

{Аналогично для вектора b}

writeln ('Вектор b');

for j:=1 to m do begin

b[j]:=random*10;

writeln (b[j]:6:2);

end;

{Умножение совмещаем с выводом вектора с,

это возможно, т.к. компоненты вектора

ищутся последовательно}

writeln ('Вектор c=A*b');

for i:=1 to n do begin

c[i]:=0; {c[i] - сумма}

for j:=1 to m do

c[i]:=c[i]+A[i,j]*b[j];

writeln (c[i]:6:2);

end;

end.