Программа экзамена по курсу Математика 1 семестр 2021ФАВТ (1). Программа экзамена по курсу математика (1 семестр, 20212022 уч г.)

Название	Программа экзамена по курсу математика (1 семестр, 20212022 уч г.)
Дата	18.07.2022
Размер	23.07 Kb.
Формат файла
Имя файла	Программа экзамена по курсу Математика 1 семестр 2021ФАВТ (1).docx
Тип	Программа экзамена #632598

Программа экзамена по курсу

МАТЕМАТИКА (1 семестр, 2021/2022 уч.г.)

Направления подготовки:

09.03.02 Информационные системы и технологии

27.03.04. Управление в технических системах

Матрицы. Линейные операции над матрицами, умножение матриц. Определение, свойства. Транспонирование матрицы, след матрицы. Определение, свойства.
Определители матриц. Определители 2, 3, n – порядка: определение. Алгебраическое дополнение, минор элемента. Теорема Лапласа. Свойства определителей.
Обратная матрица: определение, формула обратной матрицы. Нахождение обратной матрицы с помощью элементарных преобразований.
Системы линейных уравнений (СЛУ): основные понятия. Равносильные СЛУ. Методы решения СЛУ: матричный способ решения СЛУ, теорема Крамера, метод Гаусса. Обоснование, алгоритмы.
Арифметические векторы. Операции над арифметическими векторами. Линейная зависимость/независимость системы арифметических векторов.
Ранг матрицы. Свойства ранга матрицы. Нахождение ранга матрицы.
Критерий совместности СЛУ. Теорема Кронекера-Капелли.
Однородные системы линейных уравнений. Фундаментальная система решений однородной СЛУ.
Геометрические векторы. Скалярное, векторное и смешанное произведения векторов. Определение, свойства, приложения в решении метрических задач.
Уравнения линии на плоскости. Различные уравнения прямой на плоскости. Взаимное расположение прямых на плоскости. Расстояние от точки до прямой, угол между прямыми.
Различные уравнения плоскости и прямой в пространстве. Взаимное расположение плоскостей и прямых в пространстве. Расстояние от точки до плоскости, угол между плоскостями.
Канонические уравнения кривых второго порядка: эллипс, окружность, гипербола, парабола. Основные характеристики кривых второго порядка.
Общее уравнение поверхностей второго порядка. Классификация поверхностей второго порядка. Построение методом сечения.
Векторное пространство. Определение и примеры. Свойства операций векторного пространства.
Линейная зависимость/независимость системы векторов векторного пространства. Свойства линейно зависимых систем
Базис системы векторов. Свойства базиса. Ранг системы векторов. Базис векторного пространства. Размерность пространства. Координаты вектора.
Евклидовы пространства: определение, примеры. Модуль вектора, величина угла между векторами: определение, свойства. Ортонормированный базис. Ортогонализация базиса. Свойство скалярного произведения в ортонормированном базисе.
Связь координат вектора в разных базисах. Матрица преобразования координат (перехода) от базиса к базису.
Линейный оператор: определение, примеры. Матрица линейного оператора.
Матрица линейного оператора в различных базисах. Собственные значения и собственные векторы линейного оператора: определения, свойства, алгоритм нахождения. Спектр линейного оператора.
Квадратичные формы над R. Общее уравнение линий второго порядка. Классификация линий второго порядка Приведение уравнения второго порядка к каноническому виду
Множество действительных чисел. Геометрическая интерпретация множества действительных чисел. Окрестность точки. Модуль действительного числа.
Общее понятие функции. Функция одного действительного переменного. Задание функций, свойства функций: область определения, множество значений, четность-нечетность, периодичность, монотонность, ограниченность.
Элементарные функции: линейная, квадратичная. степенная, показательная, логарифмическая, тригонометрические ( 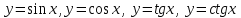), обратные тригонометрическим ( ).
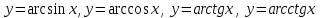Числовые последовательности и их свойства. Предел числовой последовательности.
Предел функции в точке и на бесконечности: определение, основные теоремы о пределах. Односторонние пределы.
Бесконечно малые и бесконечно большие функции: определение, свойства, примеры.
Методы раскрытия неопределенностей при вычислении пределов. Замечательные пределы.
Непрерывность функций. Классификация точек разрыва.

Литература:
1.Лубягина, Е. Н.  Линейная алгебра : учебное пособие для вузов / Е. Н. Лубягина, Е. М. Вечтомов. — 2-е изд. — Москва : Издательство Юрайт, 2021. — 150 с. — (Высшее образование). — ISBN 978-5-534-10594-0. — Текст : электронный // Образовательная платформа Юрайт [сайт]. — URL: https://urait.ru/bcode/475493 (дата обращения: 16.12.2021).
2. Потапов, А. П.  Линейная алгебра и аналитическая геометрия : учебник и практикум для вузов / А. П. Потапов. — Москва : Издательство Юрайт, 2021. — 309 с. — (Высшее образование). — ISBN 978-5-534-01232-3. — Текст : электронный // Образовательная платформа Юрайт [сайт]. — URL: https://urait.ru/bcode/469794 (дата обращения: 16.12.2021).

3.Лунгу, К. Н. Высшая математика: руководство к решению задач : учебное пособие / К. Н. Лунгу, Е. В. Макаров. – 3-е изд., перераб. – Москва : Физматлит, 2013. – Часть 1. – 217 с. – Режим доступа: по подписке. – URL: https://biblioclub.ru/index.php?page=book&id=275606 (дата обращения: 16.12.2021). – Библиогр. в кн. – ISBN 978-5-9221-1500-1. – Текст : электронный
4.Богомолов, Н. В.  Математика. Задачи с решениями в 2 ч. Часть 1 : учебное пособие для вузов / Н. В. Богомолов. — 2-е изд., испр. и доп. — Москва : Издательство Юрайт, 2021. — 439 с. — (Высшее образование). — ISBN 978-5-534-07535-9. — Текст : электронный // Образовательная платформа Юрайт [сайт]. — URL: https://urait.ru/bcode/470668 (дата обращения: 16.12.2021).

5.Богомолов, Н. В.  Математика. Задачи с решениями в 2 ч. Часть 2 : учебное пособие для вузов / Н. В. Богомолов. — 2-е изд., испр. и доп. — Москва : Издательство Юрайт, 2021. — 320 с. — (Высшее образование). — ISBN 978-5-534-07533-5. — Текст : электронный // Образовательная платформа Юрайт [сайт]. — URL: https://urait.ru/bcode/470670 (дата обращения: 16.12.2021).