задания по математике. Программа кр Производная
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
Программа КР «Производная»ТеорияМеханический смысл производной. Касательная и нормаль к кривой. Геометрический смысл производной. Уравнения касательной и нормали к графику функции. Правила дифференцирования суммы, произведения и частного двух функций. Частные случаи: производные функций Производные основных элементарных функций (таблица производных). Производная параметрически заданной функции. Дополнительные вопросы (на уровни B, C): 1) второй замечательный предел; 2) дифференцирование с применением предварительного логарифмирования; 3) дифференцирование неявных функций. Тренировочные варианты на уровень А Вариант 1 Найти угловой коэффициент нормали к графику функции Составить уравнение касательной к кривой Вариант 2Составить уравнение нормали к кривой (Ответ: Вариант 3Составить уравнение касательной к кривой (Ответ: Тренировочные варианты на уровни В,С Вариант 1 Функция Найти точку кривой (Ответ: Вариант 2 Найти угол между кривыми (Ответ: Найти точку параболы Вариант 3 Найти точку кривой (Ответ: Программа КР “Интегралы”ТеорияПервообразная. Теорема об общем виде первообразной. Неопределенный интеграл и его свойства. Таблица основных интегралов. Теорема о замене переменной. Интегрирование подведением под знак дифференциала. Интегрирование по частям. Рациональная дробь. (Не)правильная рациональная дробь. Простейшие дроби. Разложение неправильной дроби на многочлен и правильную дробь и правильной дроби на простейшие. Правило интегрирования рациональных дробей. Определенный интеграл: теорема о формуле Ньютона-Лейбница, замена переменной, интегрирование по частям. Тренировочные варианты на уровень АВариант 1Является ли функция Найти одну из первообразных функции 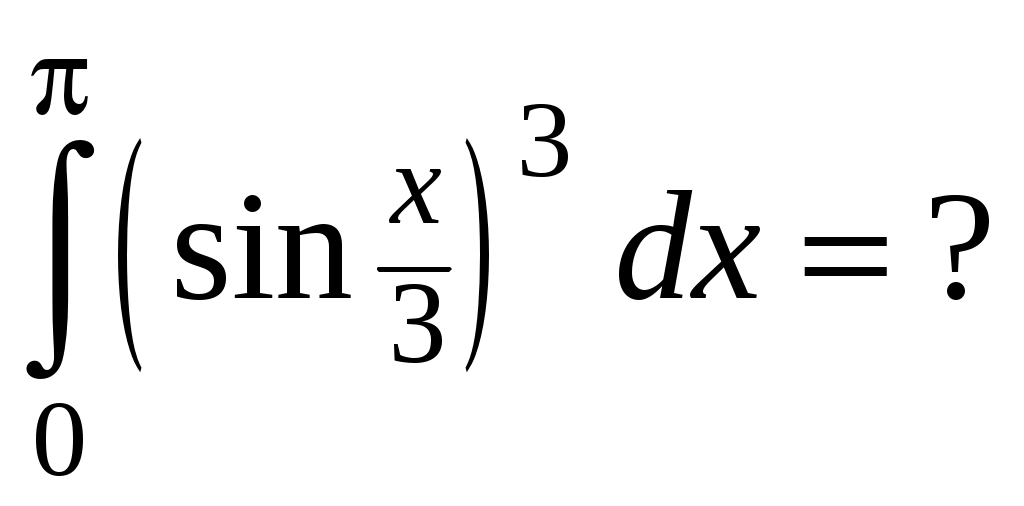 (Ответ: (Ответ: Вариант 2Найти интеграл Найти одну из первообразных функции 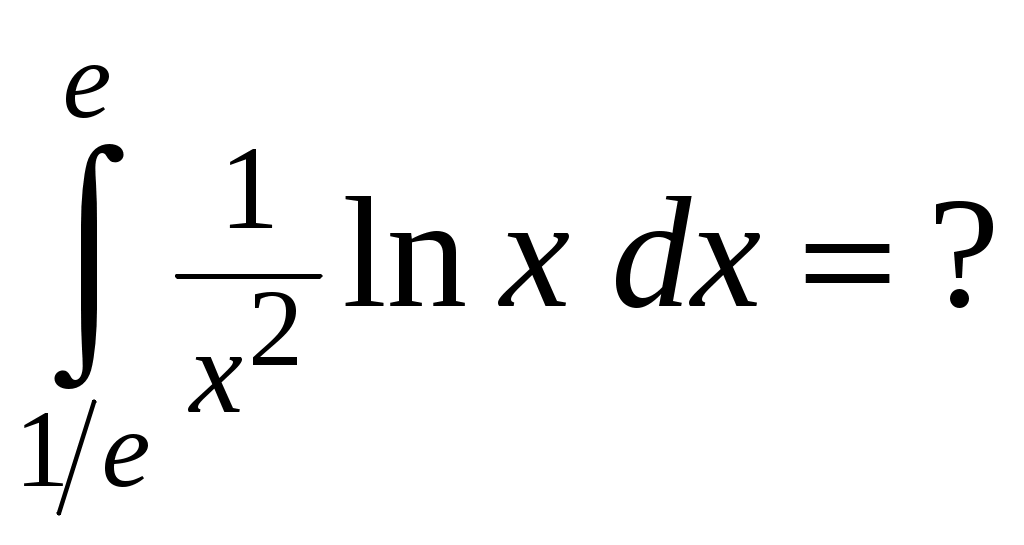 (Ответ: (Ответ: 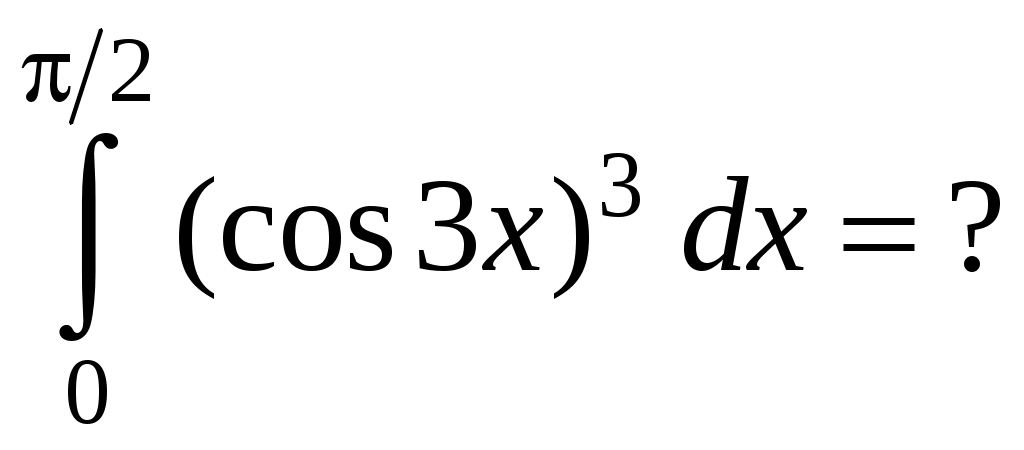 (Ответ: (Ответ: Вариант 3Написать разложение дроби (Ответ: Найти одну из первообразных функции Тренировочные варианты на уровни В, СВариант 1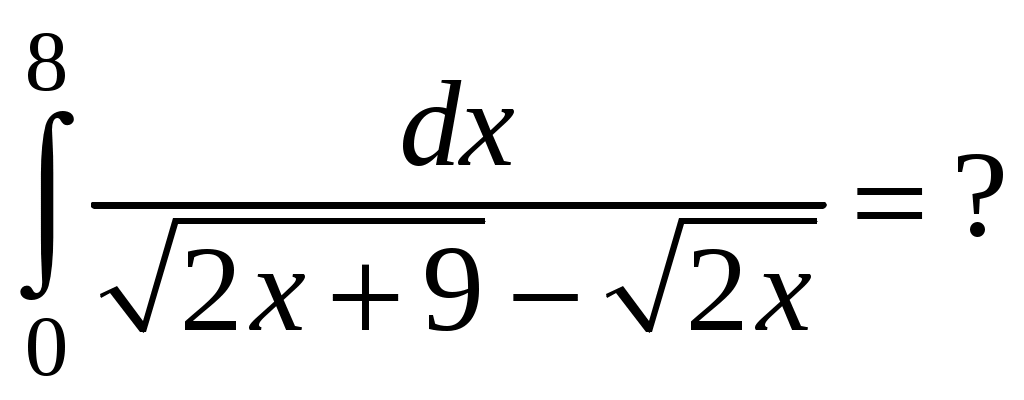 (Ответ: 6) (Ответ: 6)Вариант 2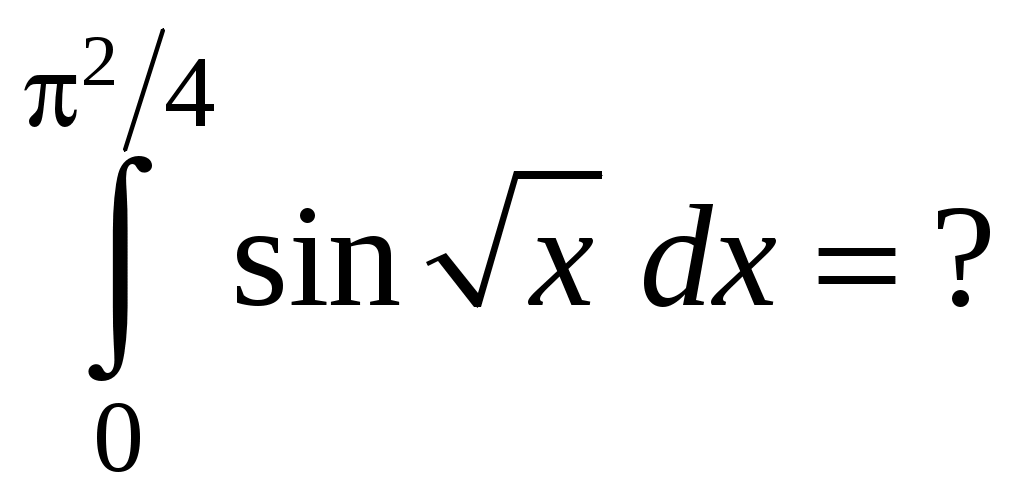 (Ответ: 2) (Ответ: 2)Вариант 3Программа КР “Функции нескольких переменных”Теория Функция двух переменных: область определения и ее геометрическое изображение, множество значений, график, приращение в точке, формула для вычисления дифференциала, приближенное вычисление приращения с помощью дифференциала. Градиент функции трех переменных, его направление и модуль. Уравнения касательной плоскости и нормали к поверхности Исследование функции двух переменных на экстремум: точка минимума (максимума, экстремума), минимум (максимум, экстремум), необходимые условия экстремума, достаточные условия экстремума. Тренировочные варианты на уровень A Вариант 1 Найти значение функции Найти и построить на плоскости (Ответ: Найти модуль градиента функции Составить уравнение касательной плоскости к поверхности (Ответ: Исследовать на экстремум функцию Вариант 2 Найти и построить на плоскости Найти градиент функции Найти приближенно (заменив дифференциалом) приращение функции Составить уравнения нормали к поверхности (Ответ: Исследовать на экстремум функцию (Ответ: функция не имеет экстремумов) Вариант 3 Найти вектор, в направлении которого функция Найти и построить на плоскости Найти модуль градиента функции Составить уравнение касательной плоскости к поверхности (Ответ: Исследовать на экстремум функцию (Ответ: Тренировочные варианты на уровни B, C Вариант 1 Найти и построить на плоскости (Ответ: Верно ли, что функция Исследовать на экстремум функцию Вариант 2 Найти и построить на плоскости (Ответ: Найти наименьшее значение функции Найти производную функции Вариант 3 Найти и построить на плоскости (Ответ: Для поверхности Исследовать на экстремум функцию Программа КР «Дифференциальные уравнения» Теория (Обыкновенное) дифференциальное уравнение (д.у.): определение, порядок, решение (частное решение), интегральная кривая. Д.у. 1-го порядка, разрешенное относительно производной: общий вид, начальное условие и его геометрический смысл, задача Коши и ее геометрическая формулировка, общее решение, поле направлений. Уравнения с разделяющимися переменными, однородные и линейные: общий вид и методы интегрирования. Д.у. 2-го порядка, разрешенное относительно второй производной: общий вид, начальные условия и их геометрический смысл, задача Коши и ее геометрическая формулировка, общее решение. Однородное линейное д.у. (о.л.д.у.) 2-го порядка: общий вид. О.л.д.у. 2-го порядка с постоянными коэффициентами: общий вид, характеристическое уравнение (х.у.), теорема о х.у., общее решение (в зависимости от вида корней х.у.). Неоднородное линейное д.у. (н.л.д.у.) 2-го порядка: общий вид, соответствующее о.л.д.у., свойства решений, теорема о структуре общего решения. Н.л.д.у. 2-го порядка с постоянными коэффициентами: общий вид, нахождение частного решения методом неопределенных коэффициентов для правой части вида Дополнительные теоретические вопросы, знание которых необходимо для решения задач на уровни B, C: теорема существования и единственности и ее геометрическая формулировка, изоклины; линейно (не)зависимая система функций, определитель Вроньского; о.л.д.у. n-го порядка: общий вид, свойства решений, линейное пространство решений, фундаментальная система решений, теорема о структуре общего решения; н.л.д.у. n-го порядка: принцип суперпозиции решений. Тренировочные варианты на уровень A Вариант 1 Что такое общее решение дифференциального уравнения Найти угол, который образует с осью x касательная к интегральной кривой дифференциального уравнения Найти кривую семейства Вариант 2 Общее решение о.л.д.у. 2-го порядка с постоянными коэффициентами в случае комплексных корней характеристического уравнения. Является ли парабола (Ответ: нет) Определить тип д. у. Вариант 3 Что такое интегральная кривая дифференциального уравнения? Является ли функция В каком виде следует искать частное решение д.у. Найти какое-нибудь частное решение д.у. Тренировочные варианты на уровни B, C Вариант 1 Изобразить на плоскости xy область(и), через каждую точку которой(ых) проходит единственная интегральная кривая уравнения Вариант 2 Доказать, что функция Вариант 3 Найти линейное дифференциальное уравнение, общее решение которого имеет вид |
