Дифуравнения. Контрольная работа 2_Матанализ. Контрольная работа 2 Задача Дифференциальные уравнения с разделяющимися переменными. Найти общее решение. 9
 Скачать 148 Kb.
|
|
КОНТРОЛЬНАЯ РАБОТА № 2 Задача 1. Дифференциальные уравнения с разделяющимися переменными. Найти общее решение. 9.  Решение. Сгруппируем слагаемые и вынесем за скобки общие множители:  Получили дифференциальное уравнение с разделяющимися переменными. Разделим обе части на 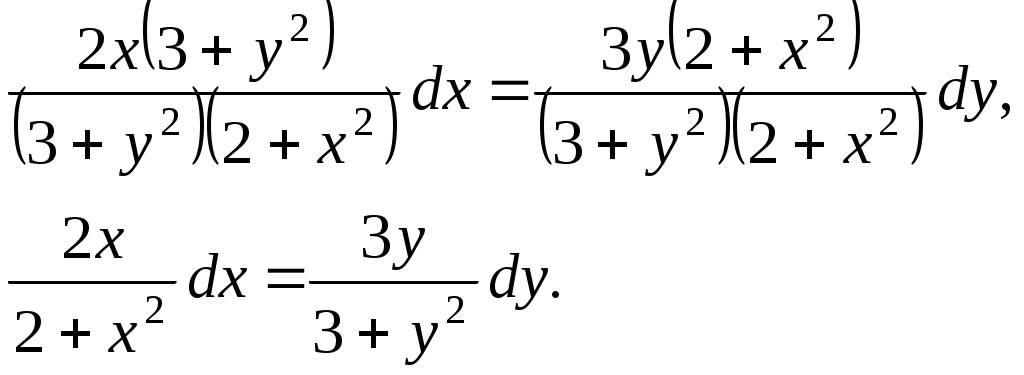 : Проинтегрируем обе части: 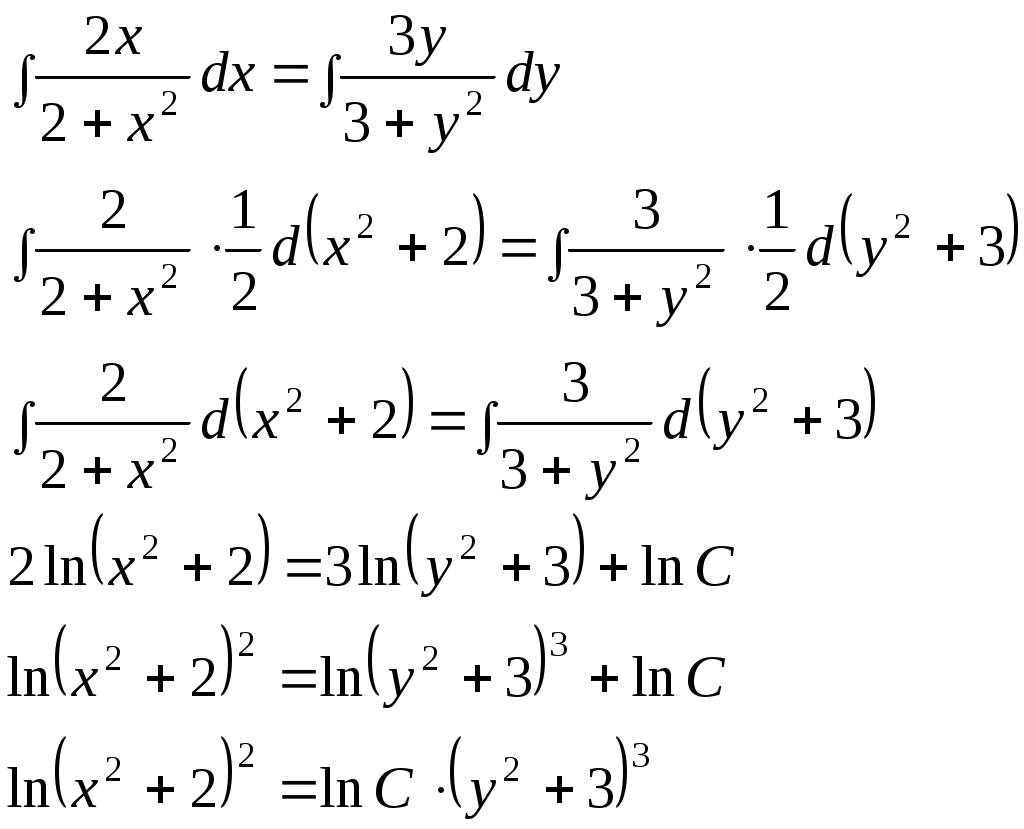  - общий интеграл дифференциального уравнения.Задача 2. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами 9.  Решение. 1) Составим и решим характеристическое уравнение: 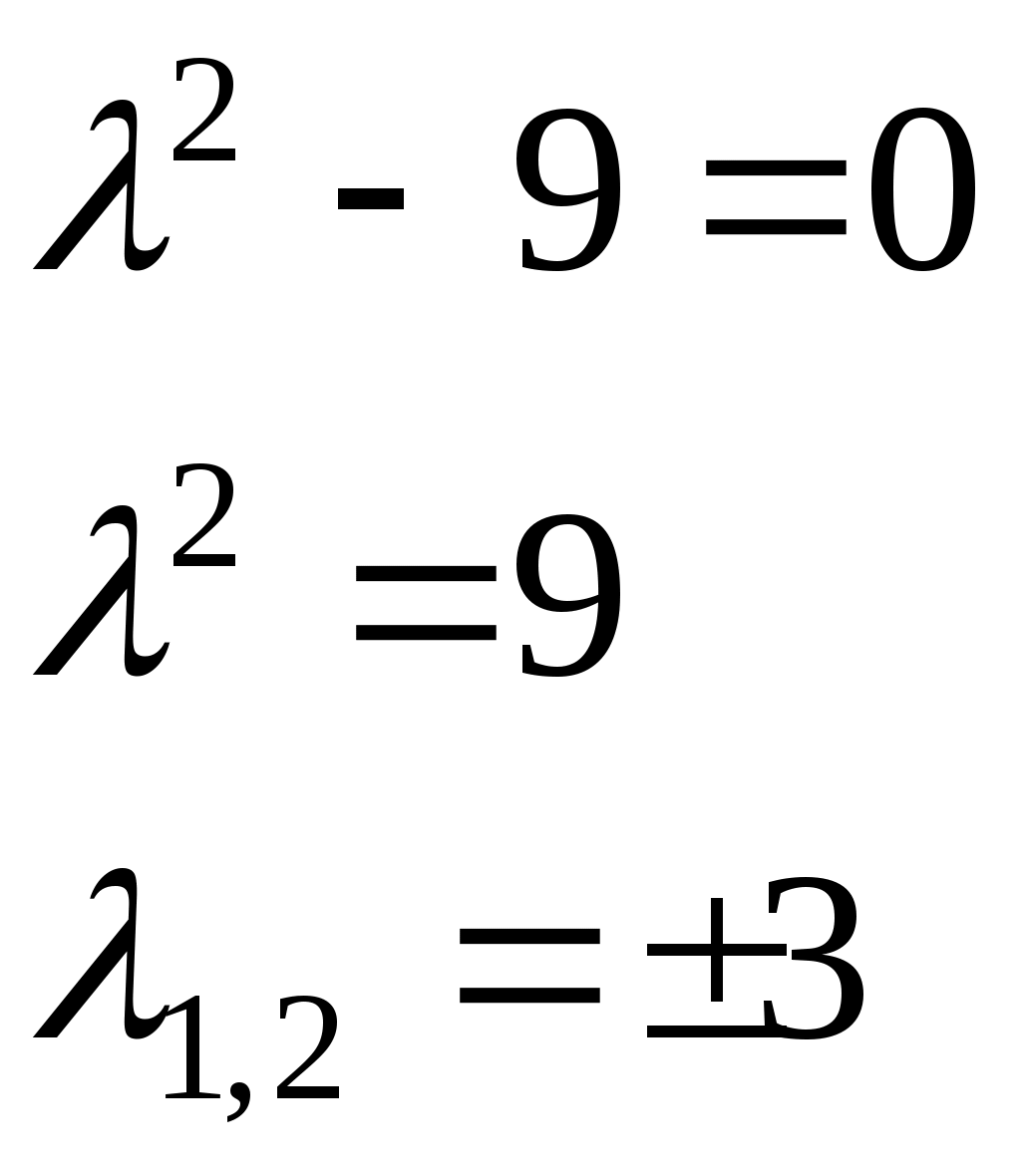 Поскольку  и  то общее решение однородного уравнения запишем в виде:  2) Найдем частное решение неоднородного уравнения. Правая часть уравнения  . Сравнивая ее с видом  заключаем =3, =0, n=0, m=0. Определим параметры частного решения. Учитывая, что =3, =0, получим, что  - однократный корень характеристического уравнения, поскольку корни  Следовательно, k = 1. l=0. Подставляя полученные параметры в  имеем:  Для определения коэффициентов А и В найдем  и   и подставим в исходное уравнение:  Итак,  3) Общее решение неоднородного дифференциального уравнения:  Задача 3. Исследовать сходимость положительного ряда, применяя какой – либо из достаточных признаков сходимости (сравнения, Даламбера, радикальный или интегральный): 9. а)  б)  с)  Решение. а) Применить признак Даламбера. Записываем n-ый член ряда:  .Тогда,  .Найдем предел отношения: 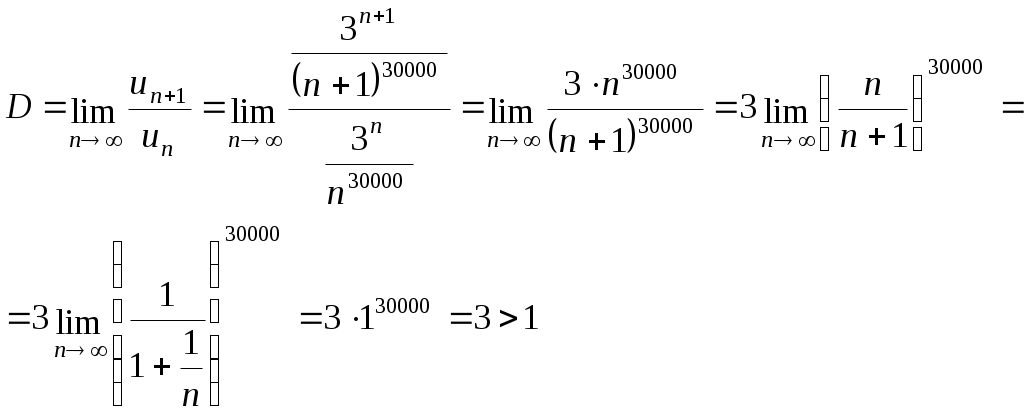 Следовательно, ряд расходится. б)  Применить признак Даламбера. Записываем n-ый член ряда:  .Тогда,  .Найдем предел отношения: 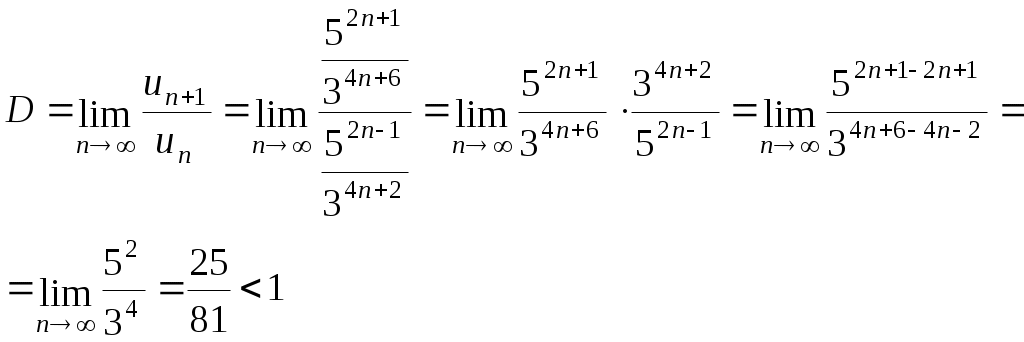 Следовательно, ряд сходится. с)  Решение. Применим первый признак сравнения. В качестве «эталонного» ряда возьмем обобщенный гармонический ряд  Показатель степени гармонического ряда p=2>, поэтому «эталонный» ряд сходящийся. Члены исходного ряда для всех n1 меньше соответствующих членов «эталонного» ряда:  Применяя первый признак сравнения, получаем, поскольку сходится «больший» эталонный ряд, то сходится и «меньший» исходный ряд. Следовательно, рассматриваемый ряд сходится. Задача 4. Найти интервал сходимости степенного ряда, исследовать его поведение на концах интервала сходимости и указать область сходимости: 9)  Решение Интервал сходимости ряда найдём с помощью признака Даламбера: 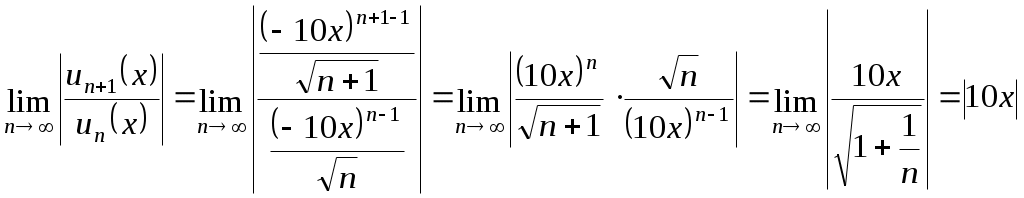 Ряд сходится при   - интервал сходимости исследуемого степенного ряда.Исследуем сходимость ряда на концах найденного интервала: 1) Подставляем значение 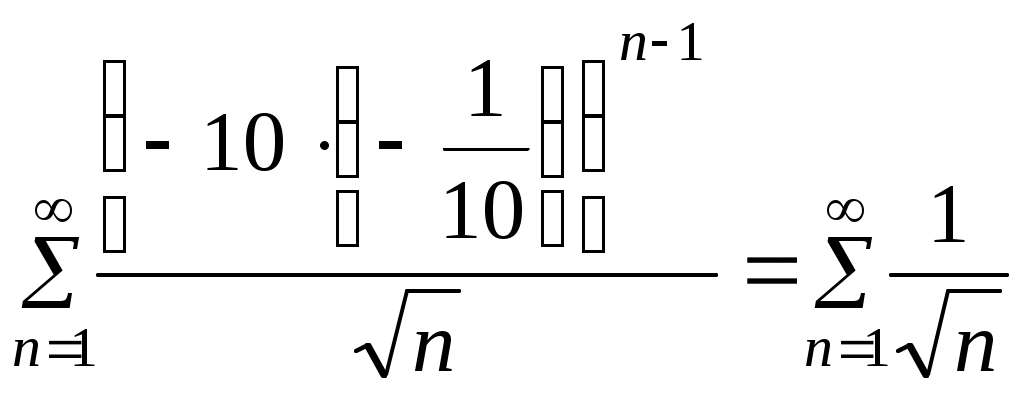 в степенной ряд  - расходится, как обобщенный гармонический ряд с показателем степени p=1/2<.2) Исследуем второй конец интервала сходимости. Подставляем значение 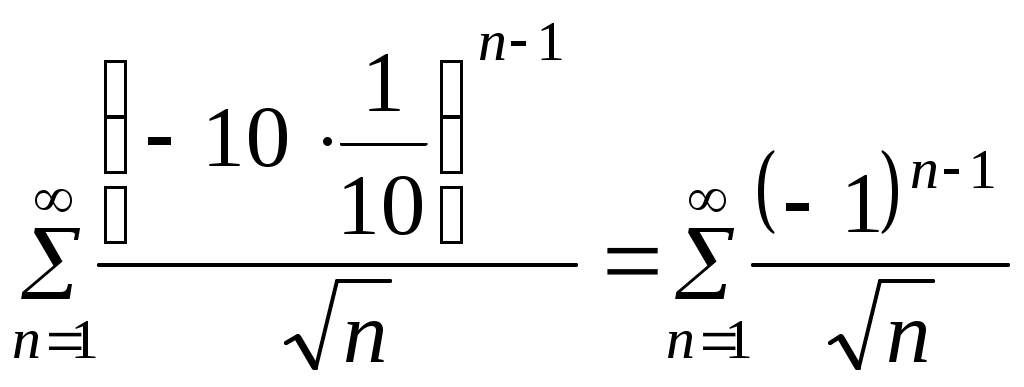 в степенной ряд  - знакочередующийся ряд.Используем признак Лейбница: – Ряд является знакочередующимся. –  – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий, значит, убывание монотонно.Вывод: ряд сходится Полученный числовой ряд не является абсолютно сходящимся поскольку  – расходится (по доказанному).Ответ:  – область сходимости исследуемого степенного ряда, при ряд сходится условно. |