|
|
11 класс алгебра — копия. Линейные однородные дифферециальные уравнения второго порядка с постоянными коэффициентами
9ПОУРОЧНЫЙ ПЛАН
Раздел:
|
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
|
ФИО педагога
|
Амантаев В.А
|
Дата:
|
12.04.2023
|
Класс:
|
Количество присутствующих:
|
Количество отсутствующих:
|
Тема урока:
|
Линейные однородные дифферециальные уравнения второго порядка с постоянными коэффициентами.
|
Цели обучения в соответствии
с учебной программой:
|
11.4.1.25. Решать линейные однородные дифференциальные уравнения 2 порядка вида ay′′ + by′ + cy = 0, где a, b, c – постоянные
|
Цели урока:
|
Отработать знания и умения а также решение задач на линейные однородные дифферециальные уравнения второго порядка с постоянными коэффициентами.
|
Ходурока
Этапурока/ Время
|
Действия педагога
|
Действияученика
|
Оценивание
|
Ресурсы
|
Приветствие, создание коллаборативной среды/ 2 мин
|
Приветствие со школьниками, определение отсутствующих. Сообщение темы и цели урока, ожидаемых результатов.
|
Принимают участие в постановке темы (цели) урока. Осмысливают поставленную цель.
|
|
|
Актуализация знаний/ 5 мин.
Проверка домашнего задания
|
Повторения пройденного материала по стратегии «Я знаю, что…..»
Корни уравнений
|
Говорят, что знают по теме урока
Взаимопроверка
|
ФО
Похвала учителя
|
|
Середина урока
35 минут
|
Данные уравнения имеют вид:
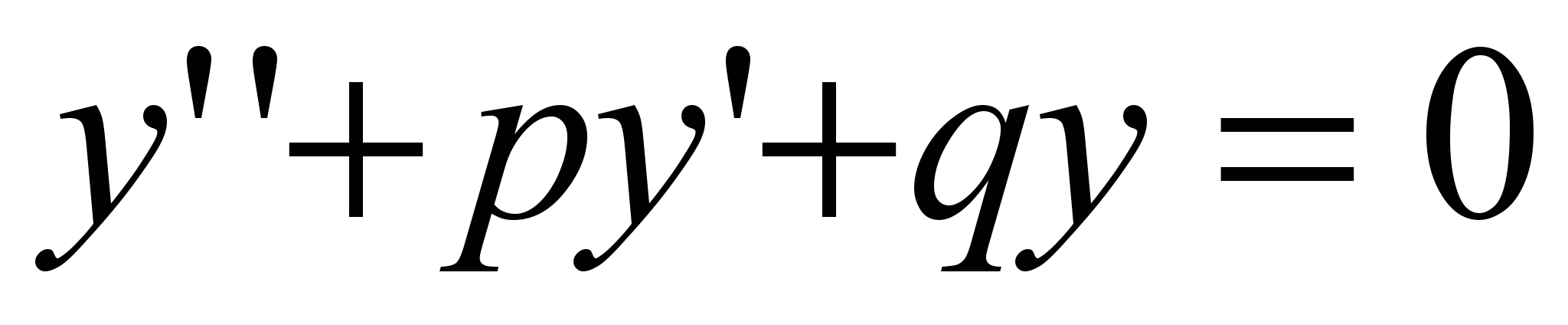 , (1) , (1)
где p и q –постоянные числа
Определение
Два решения уравнения (1) 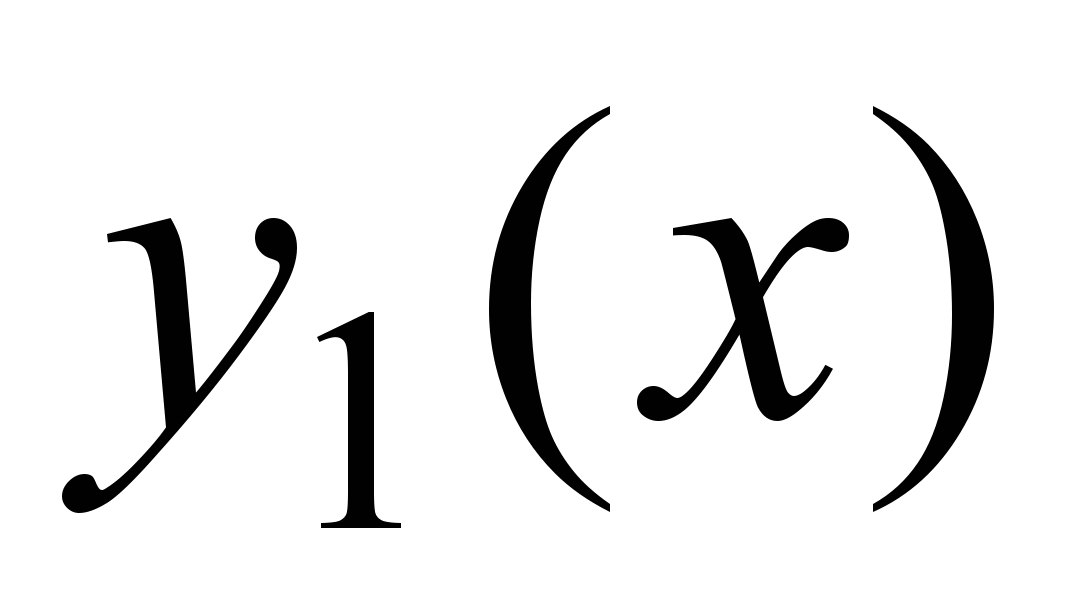 и и 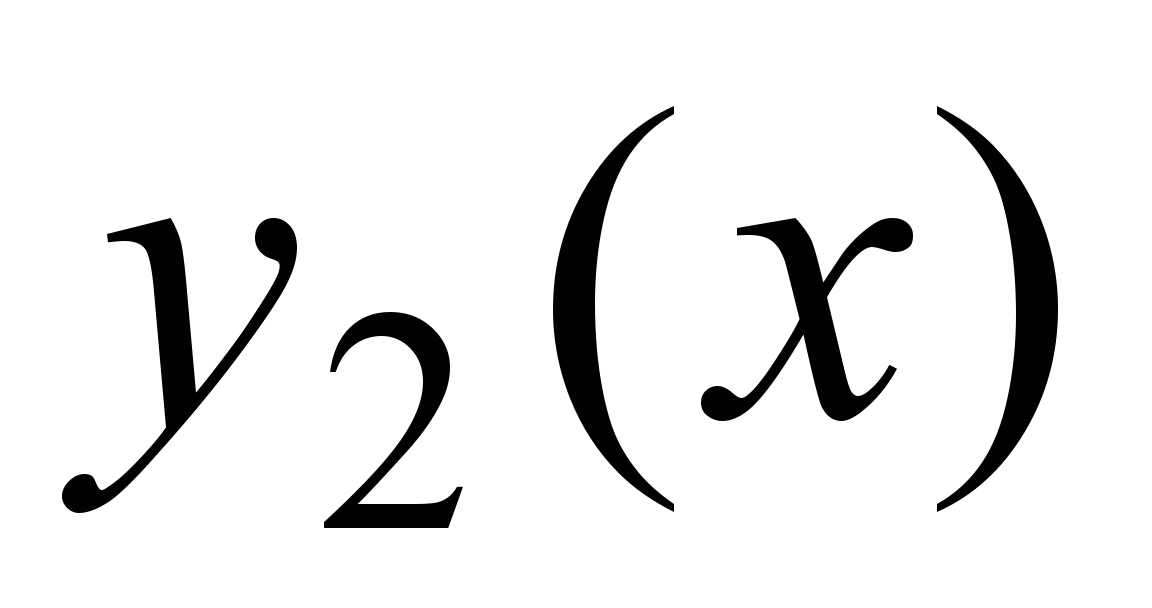 называются линейно независимыми на отрезке называются линейно независимыми на отрезке 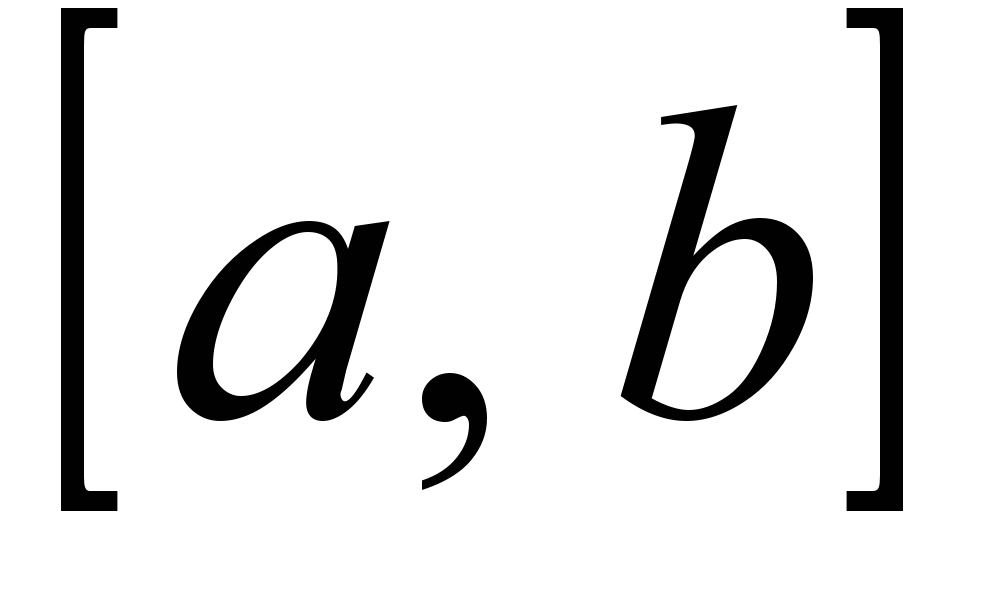 ,если их отношение на данном отрезке не является постоянным, т.е. ,если их отношение на данном отрезке не является постоянным, т.е.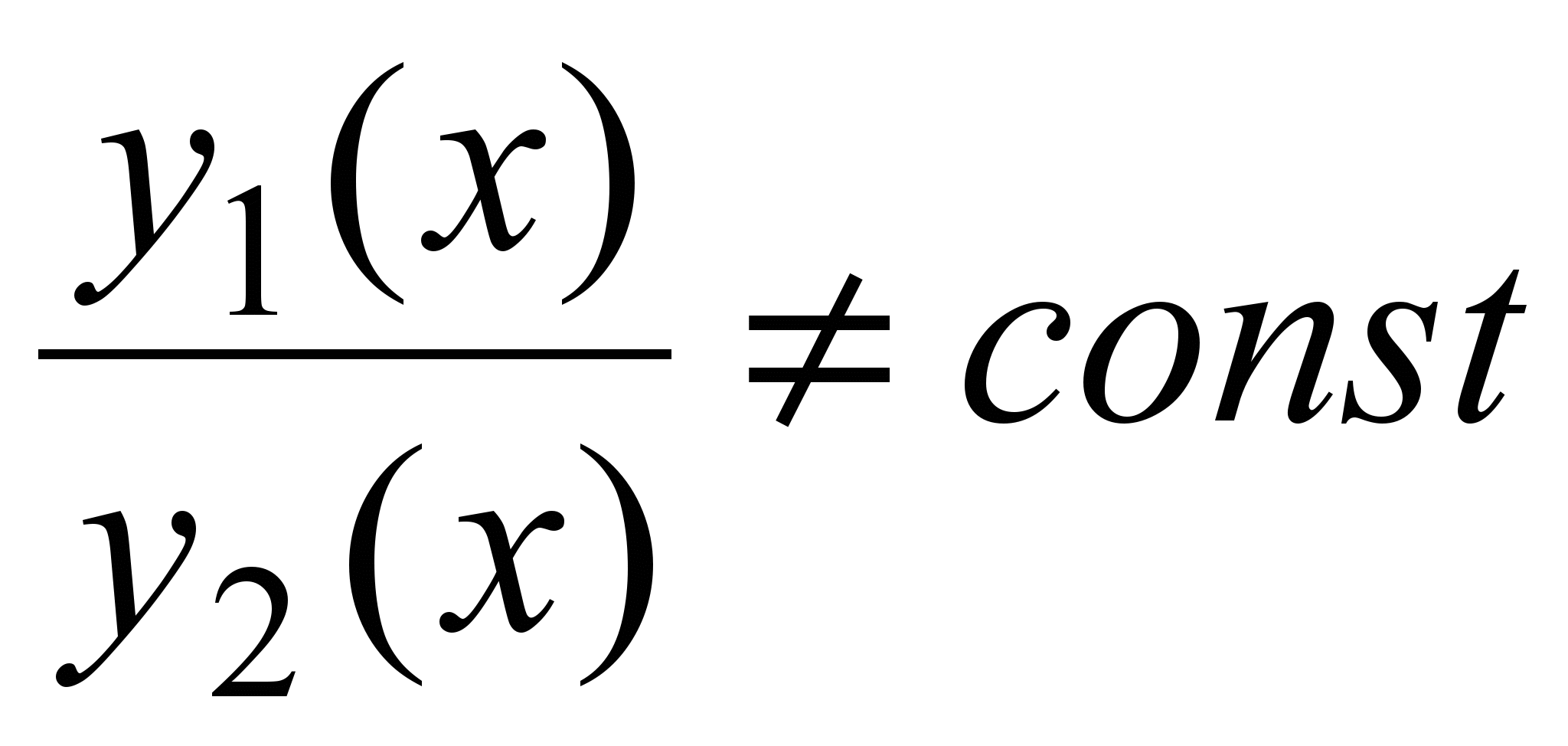 на на 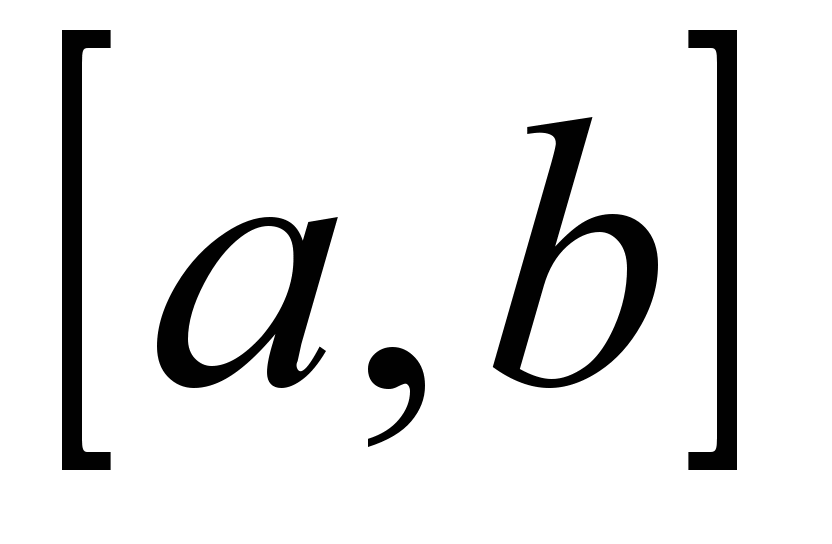
Теорема ( Об общем решении ЛОДУ)
Если 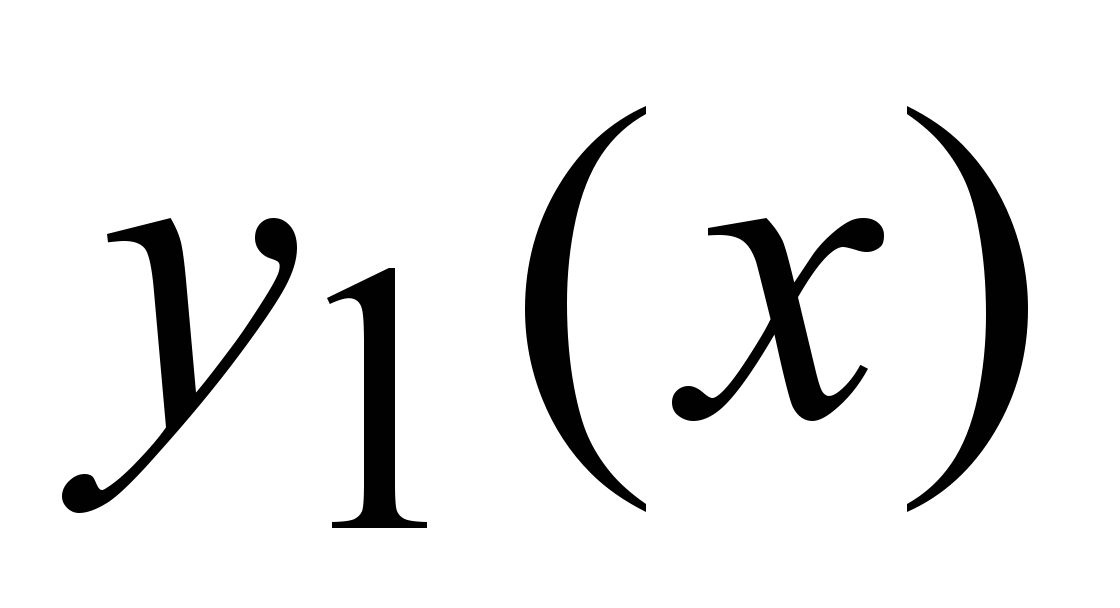 и и 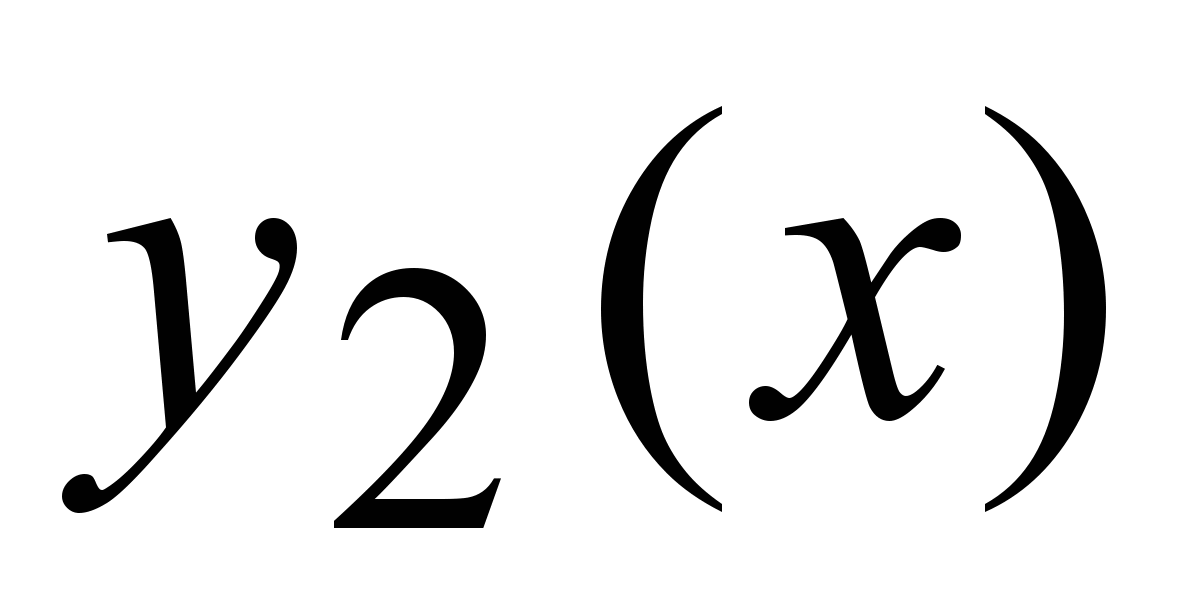 –два линейно независимых решения уравнения (1), то линейная комбинация –два линейно независимых решения уравнения (1), то линейная комбинация
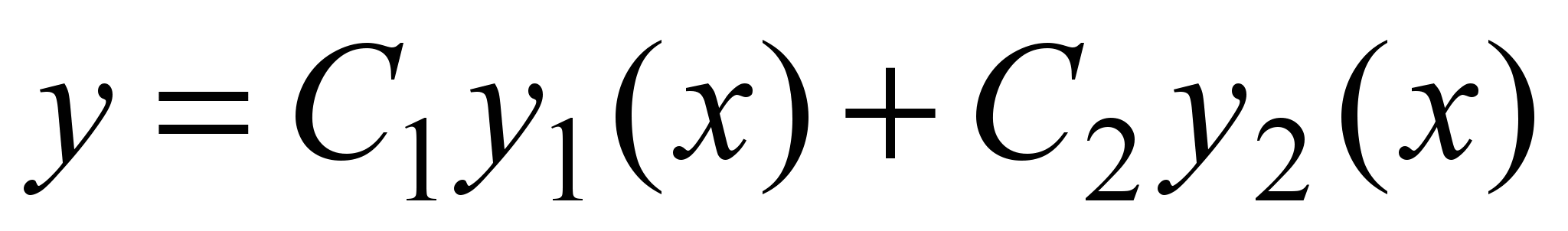 , (2) , (2)
где 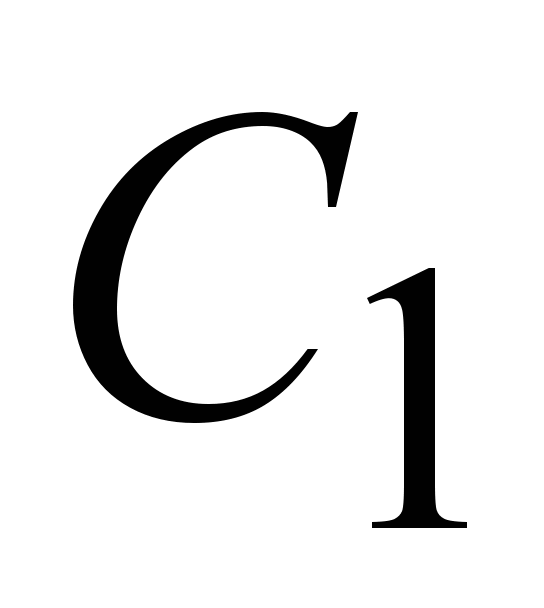 и и 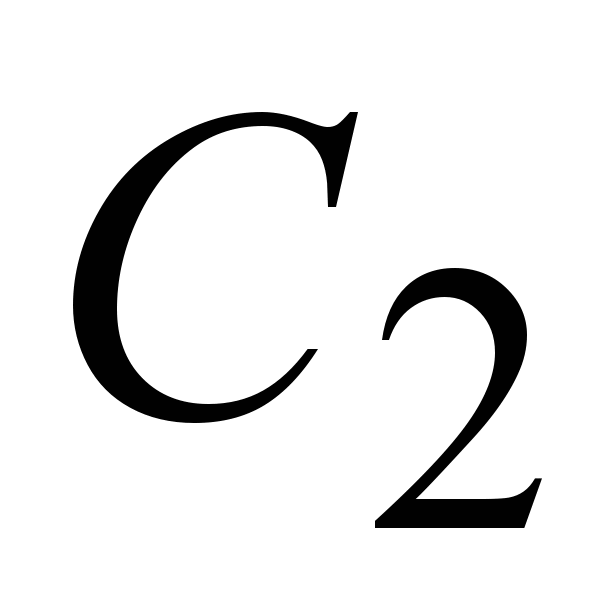 –произвольные постоянные, является его общим решением. –произвольные постоянные, является его общим решением.
Характеристическое уравнение
Для нахождения общего решения (2) следует найти два линейно независимых частных решения. Будем искать их виде 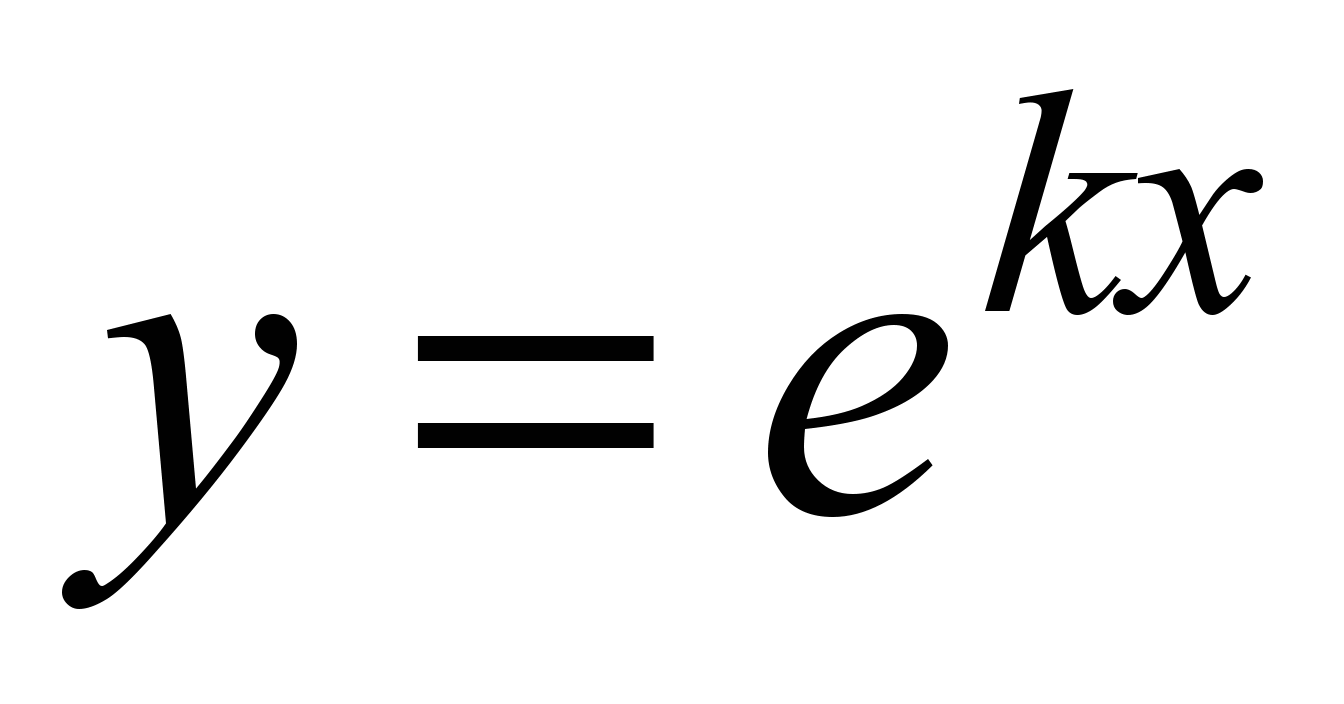 ( ( 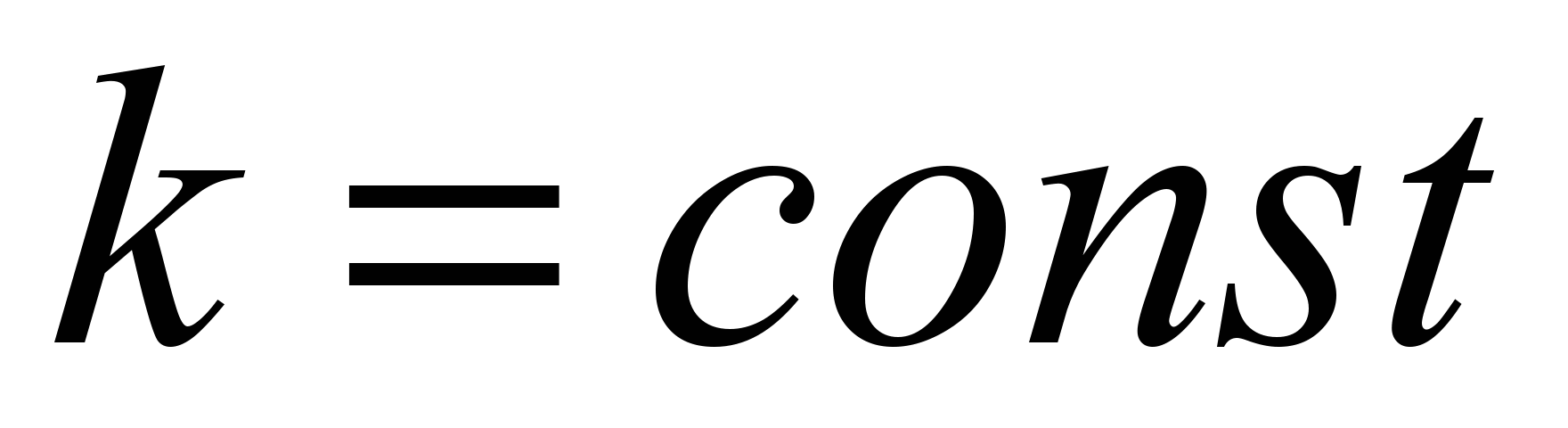 ); тогда ); тогда 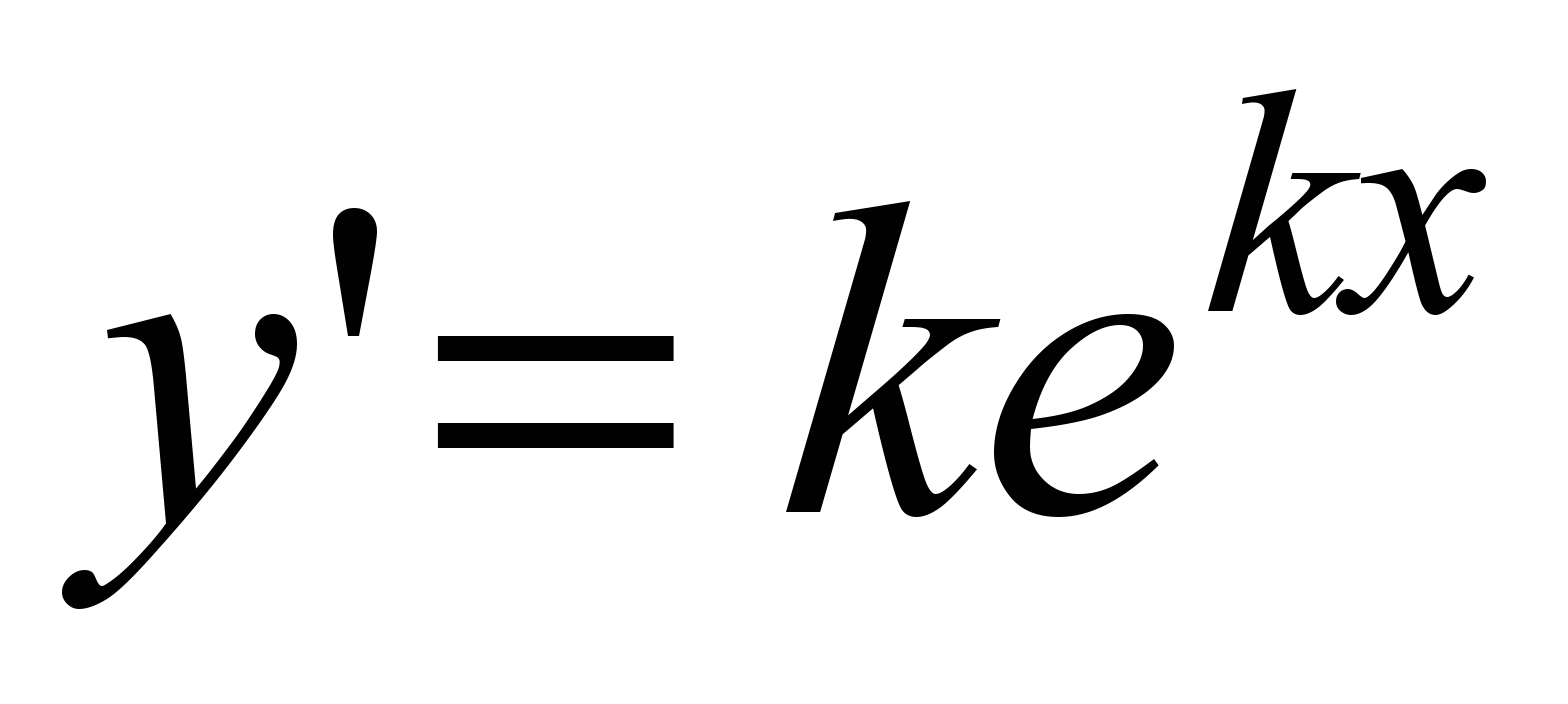 , , 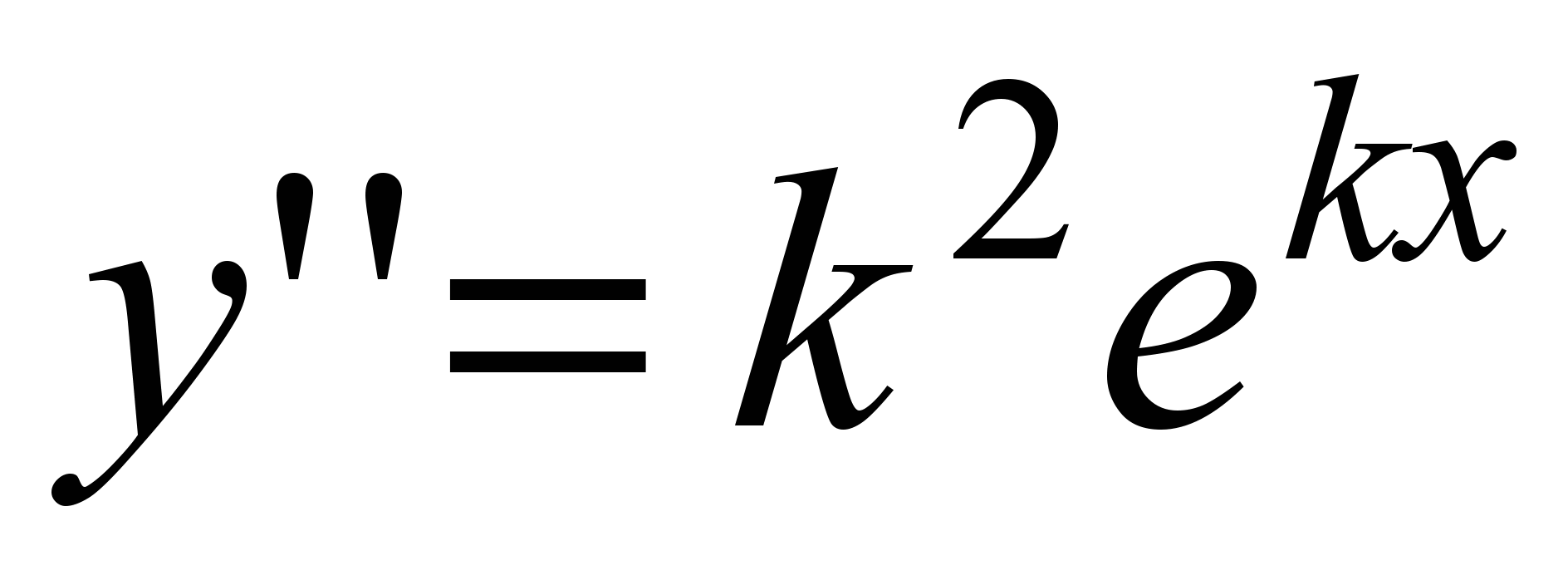 , подставим эти выражения в (1), получим , подставим эти выражения в (1), получим 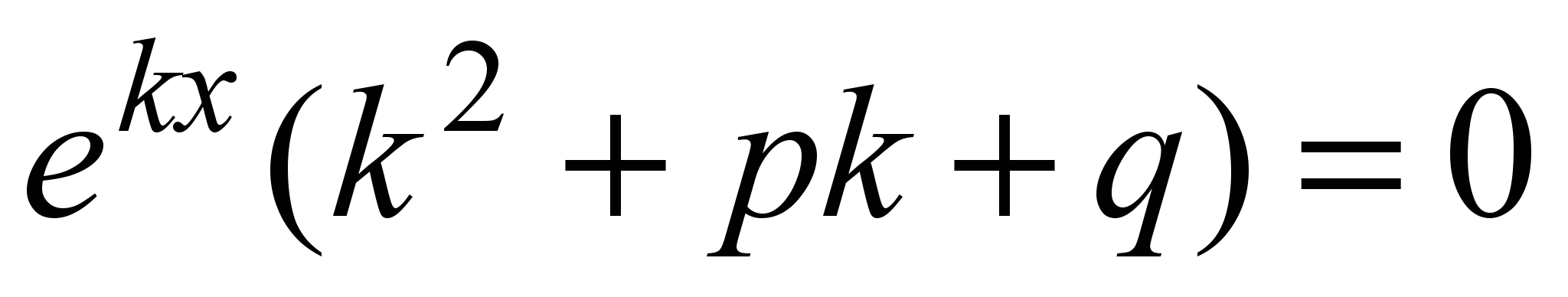 , откуда следует: , откуда следует:
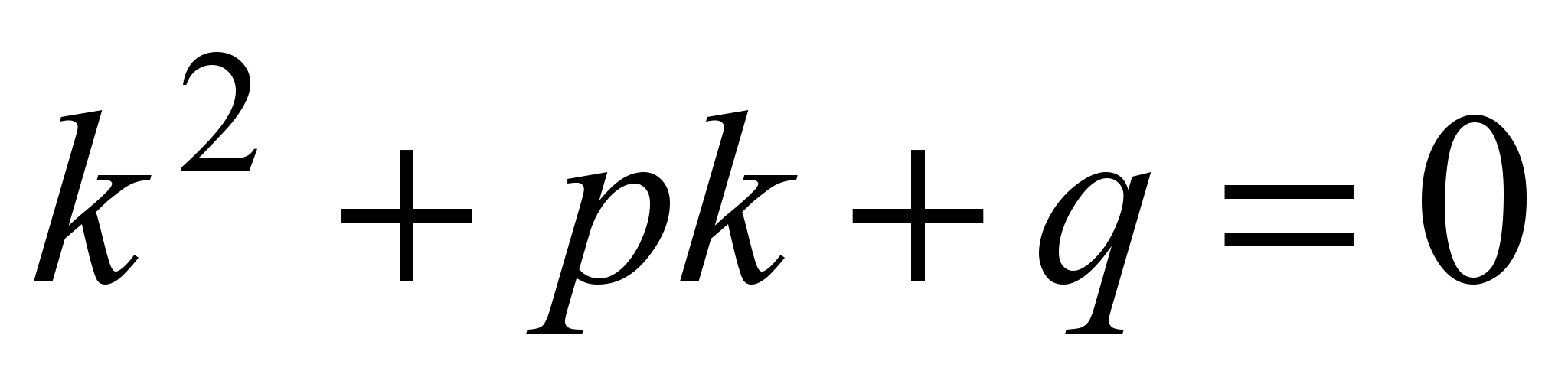 (3) (3)
-характеристическое уравнение, его корни:
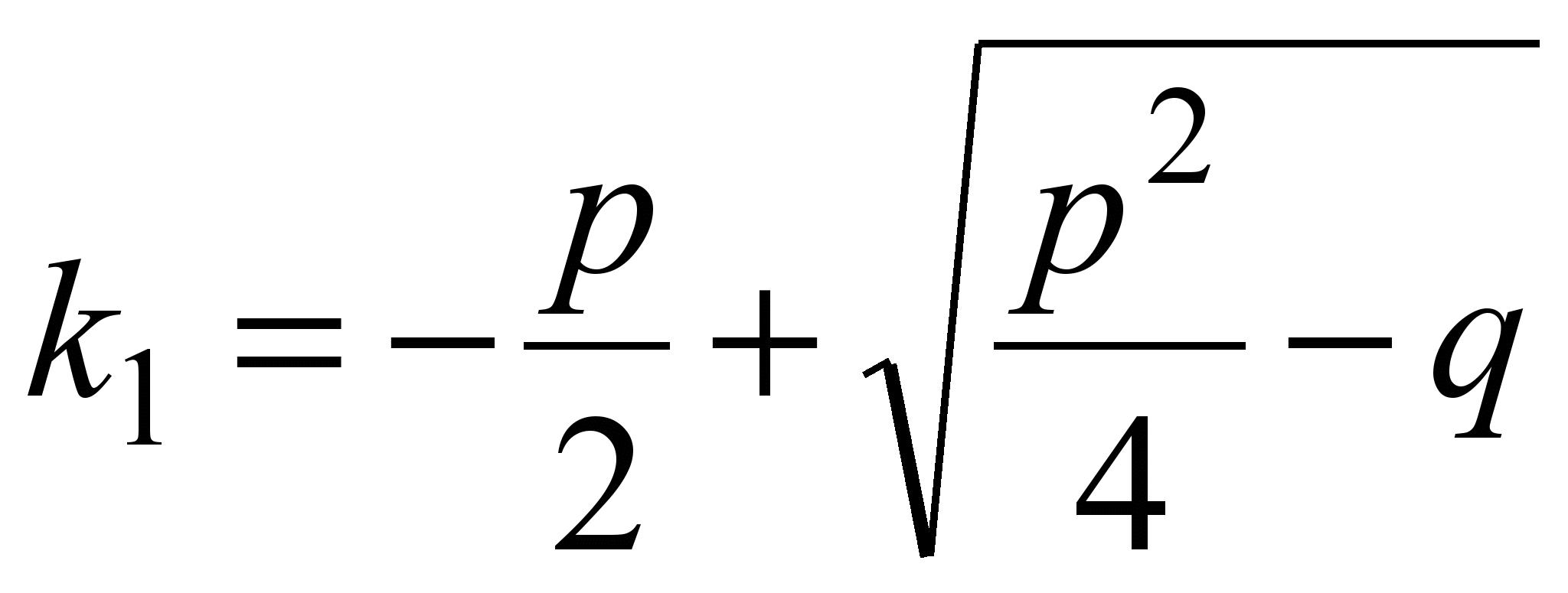 ; ; 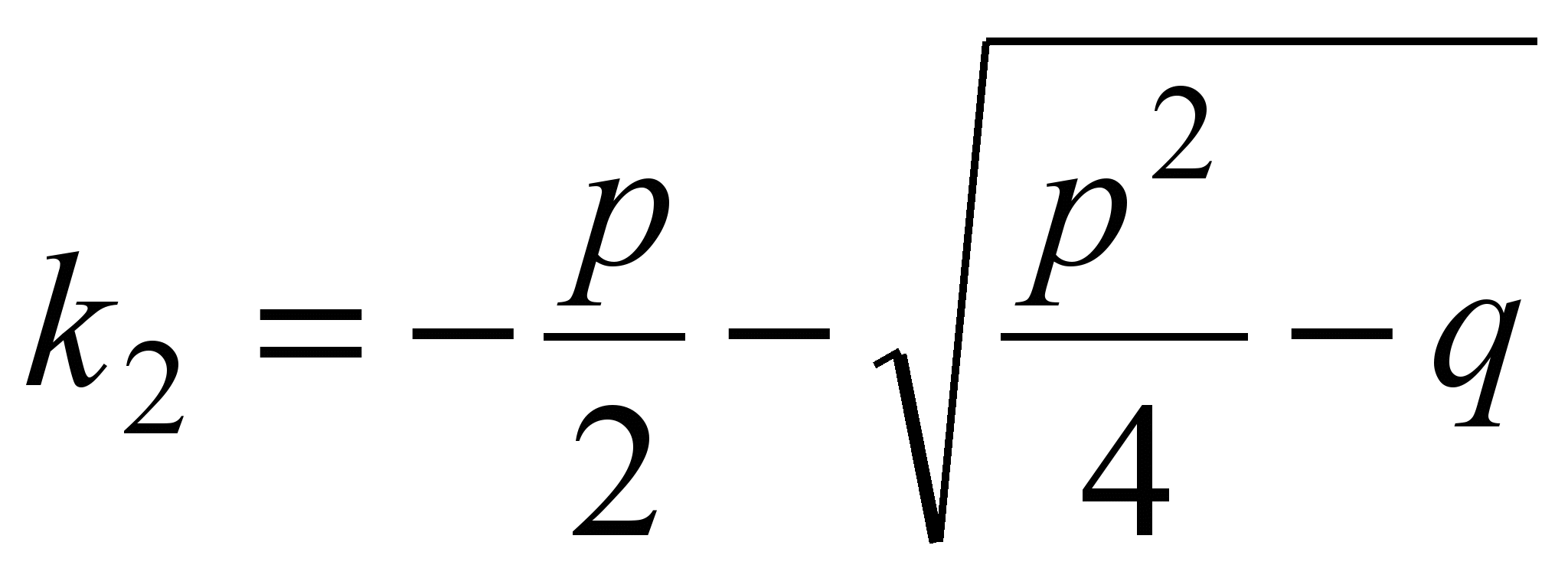 (4) (4)
Случаи решения характеристического уравнения:
I. корни 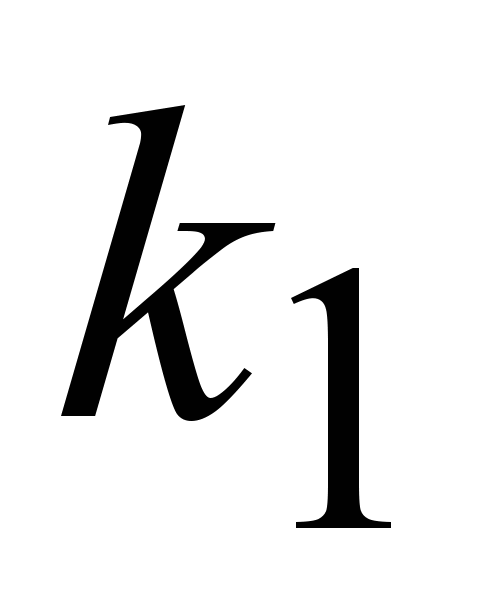 и и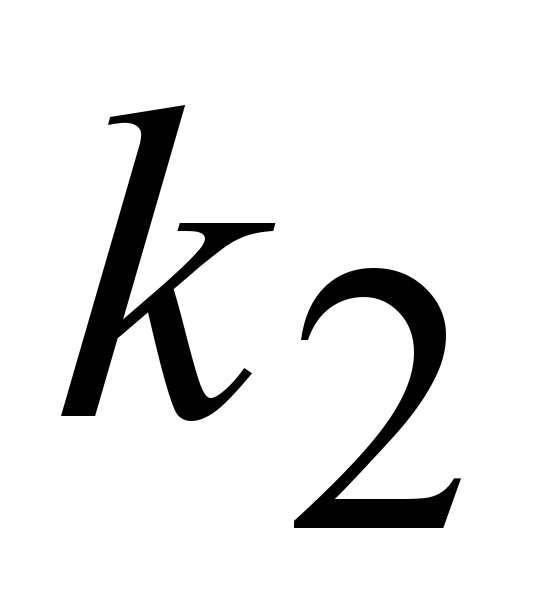 –действительные и различные (D –действительные и различные (D
II. корни 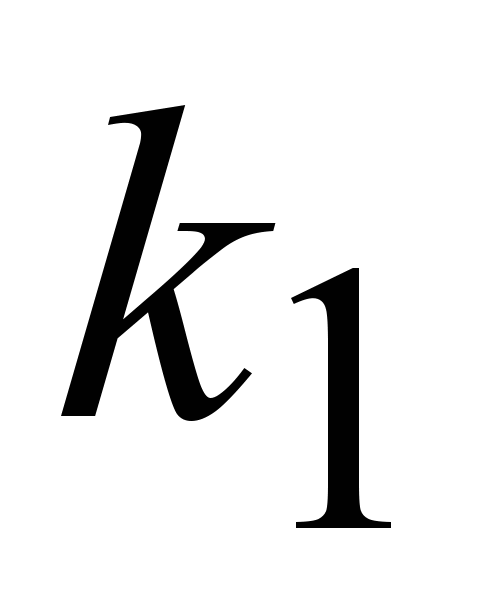 = =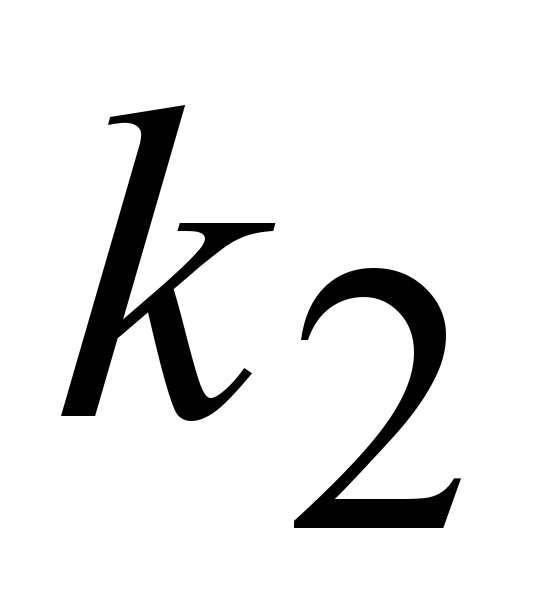 –равные действительные (D=0) –равные действительные (D=0)
III корни 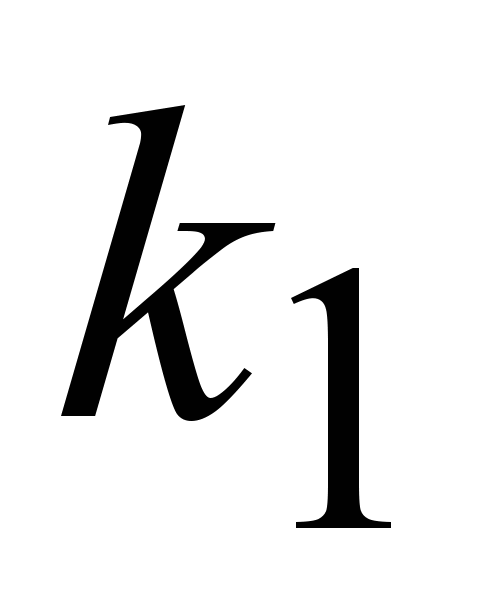 и и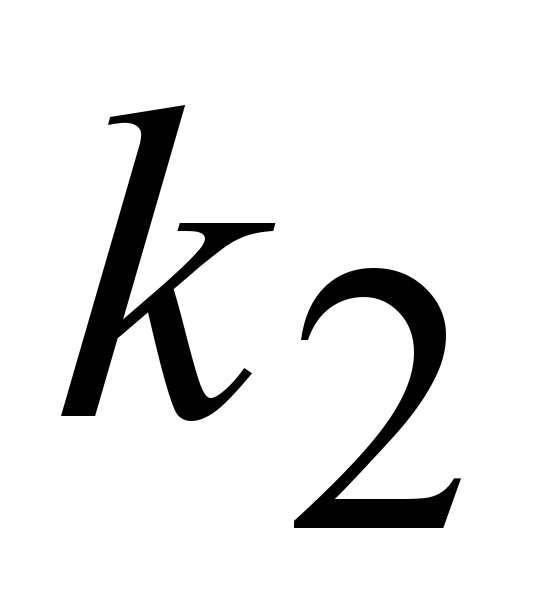 –комплексные (D<0); –комплексные (D<0);
Рассмотрим каждый случай отдельно.
I. Корни характеристического уравнения действительные и различные (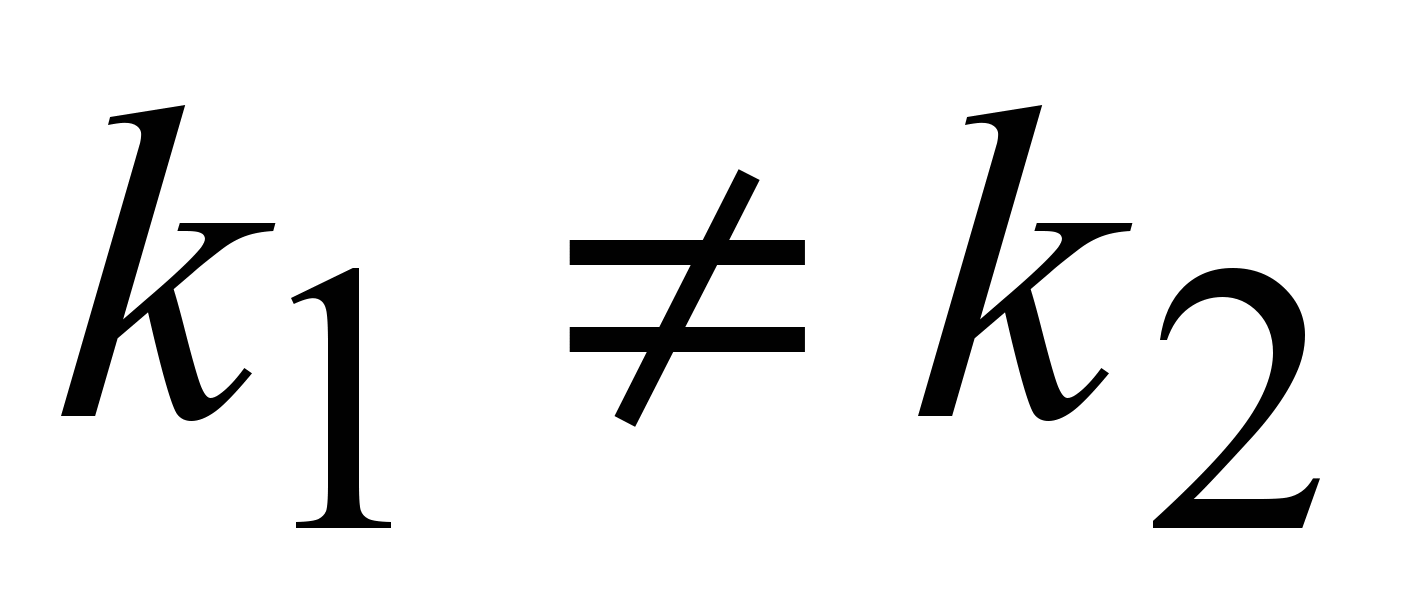 ). ).
Частными решениями будут функции 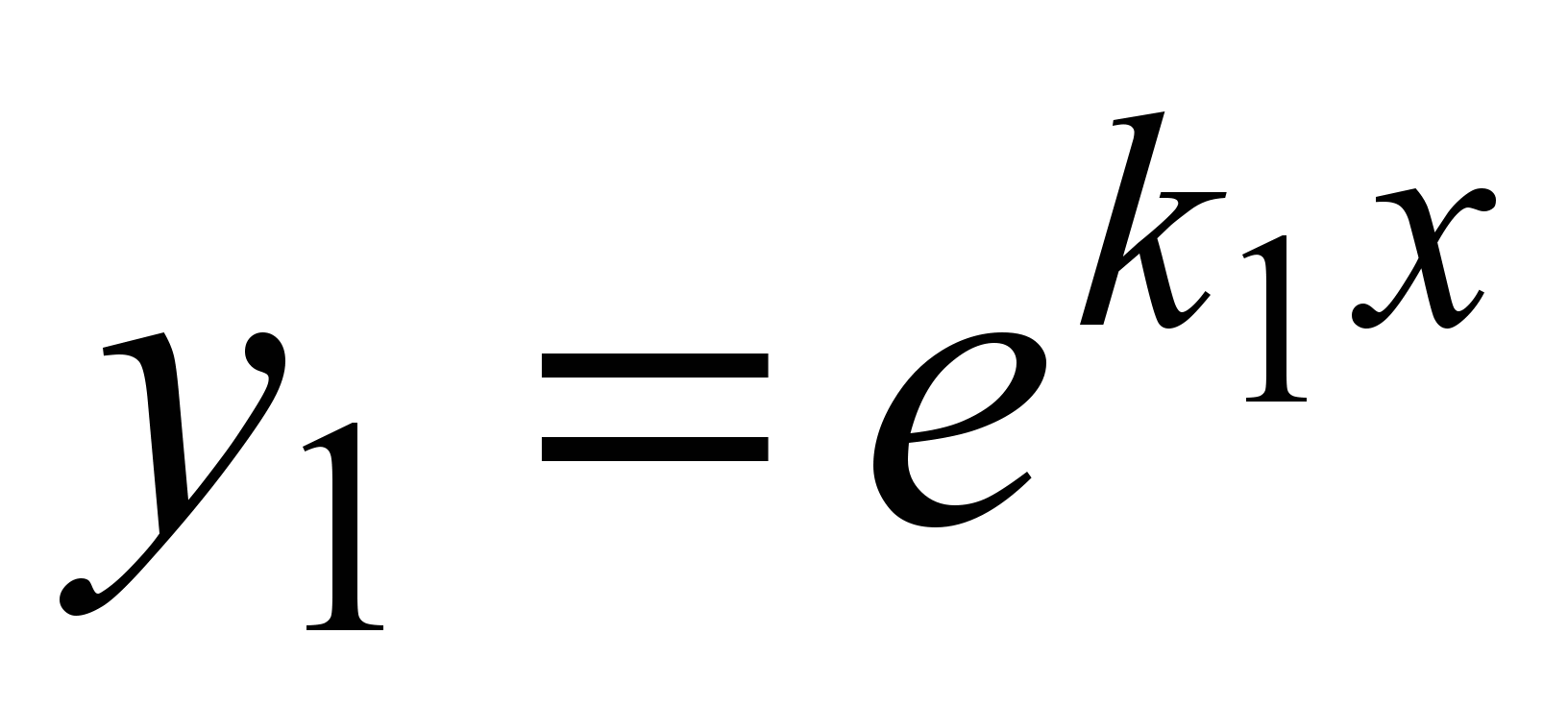 , , 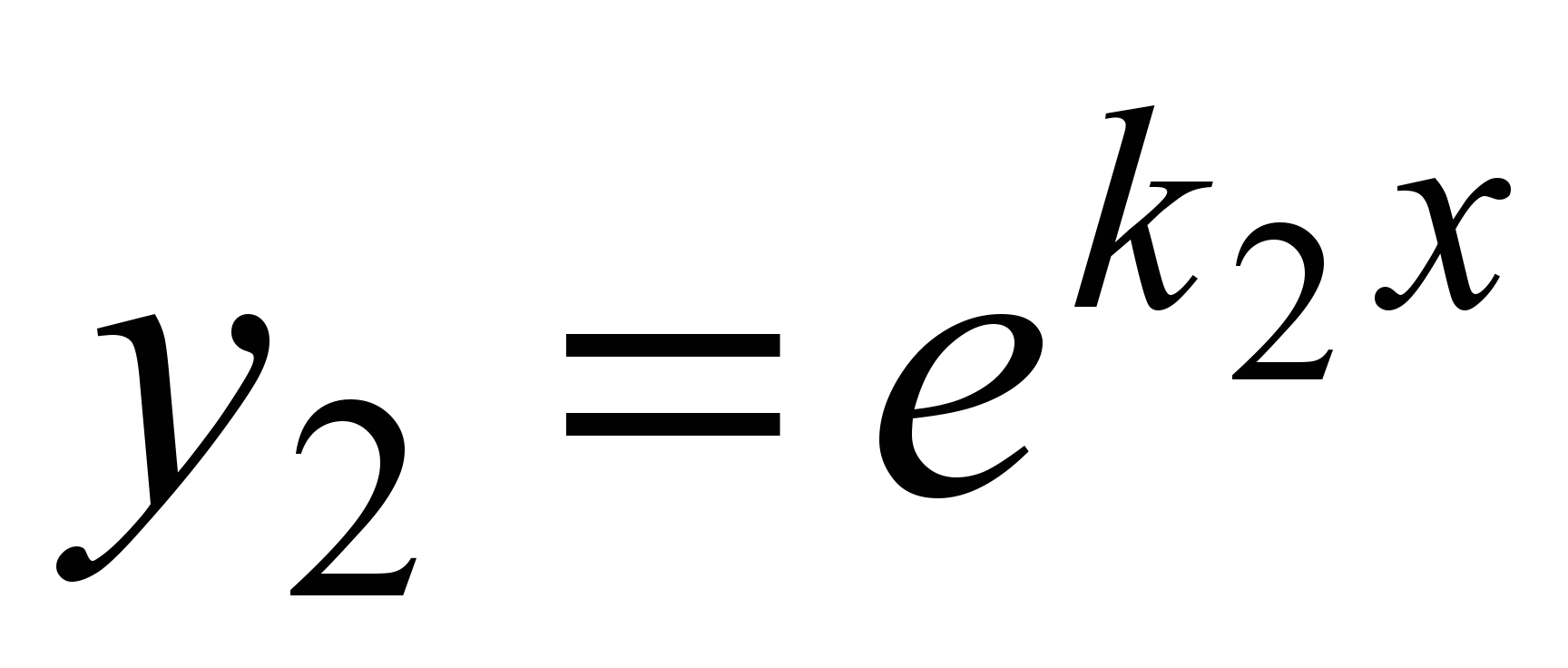
Они линейно независимы, т.к. 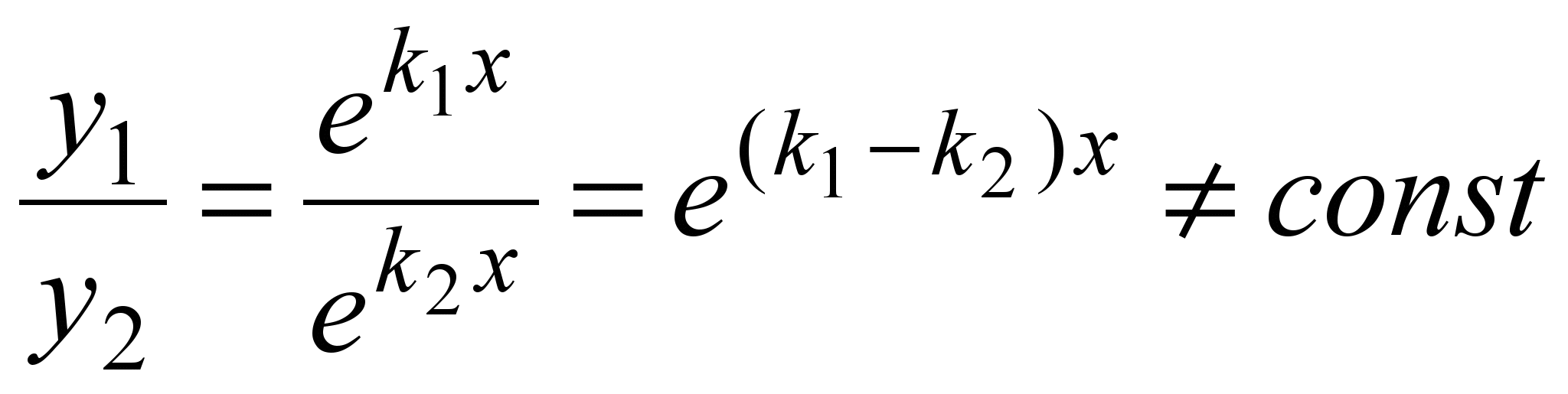
Следовательно, общее решение имеет вид: 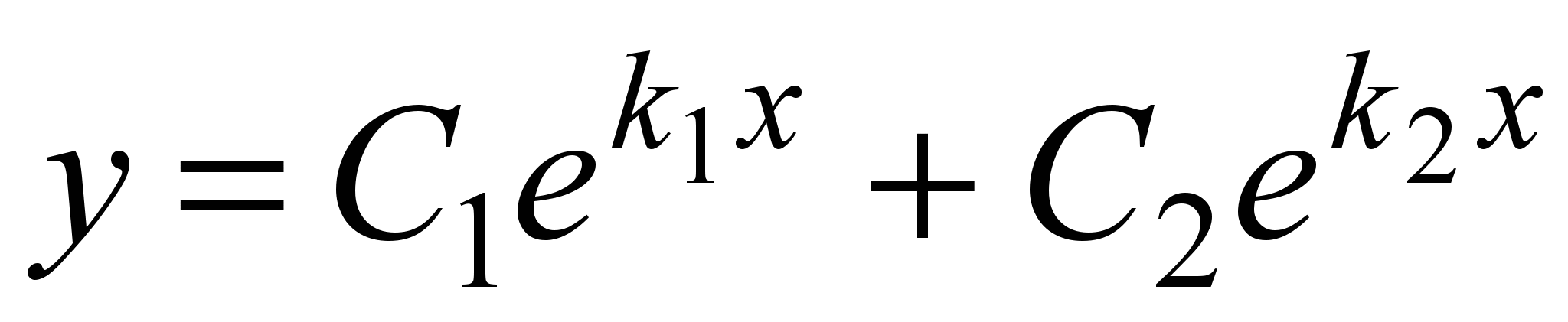
II. Корни характеристического уравнения действительные и равные (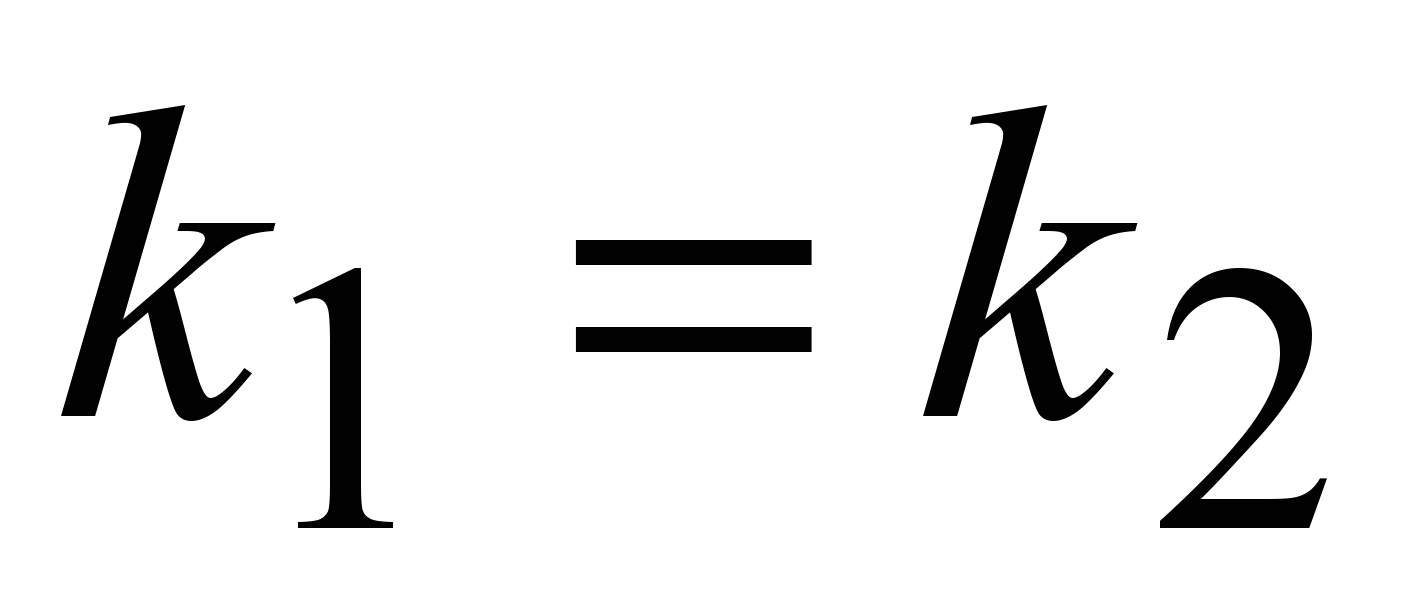 ) )
Это будет при D=0 , т.е. 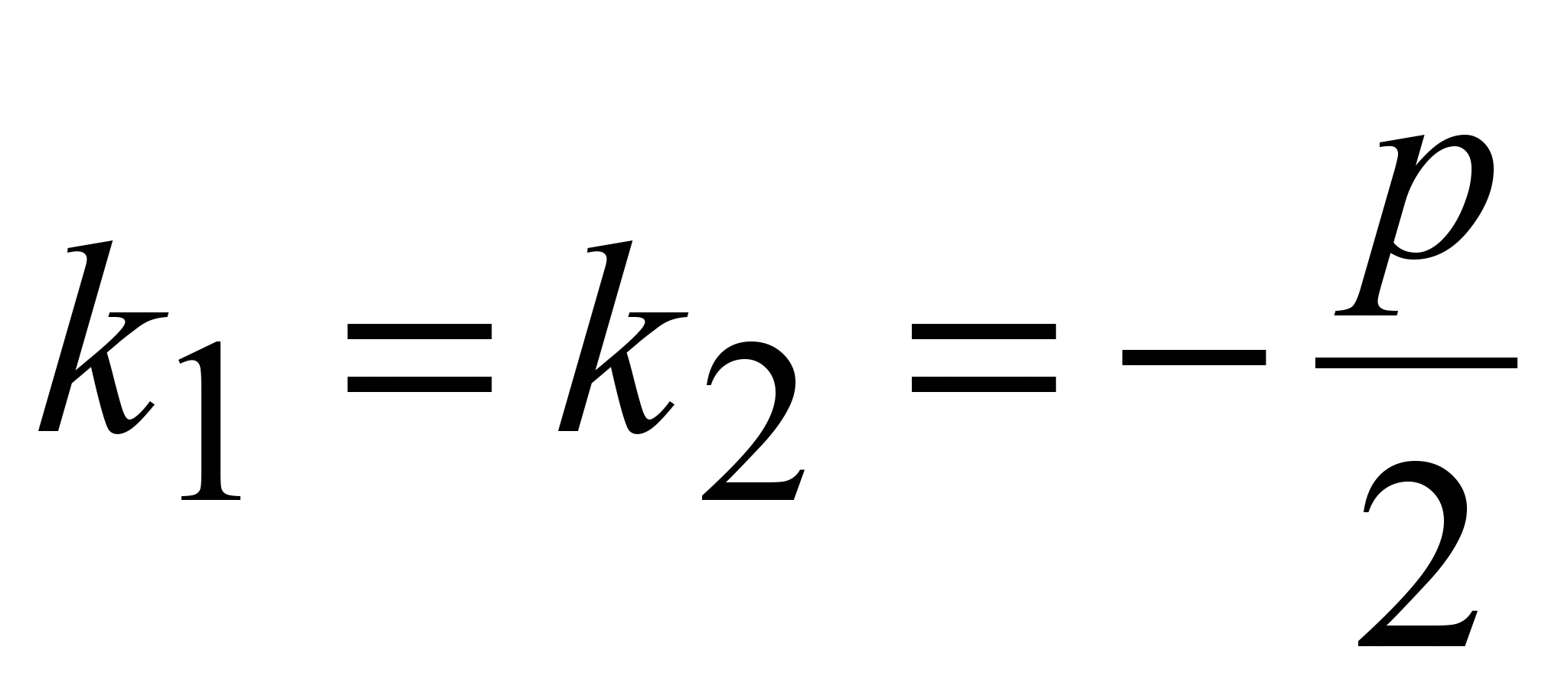 . .
В качестве первого частного решения возьмём 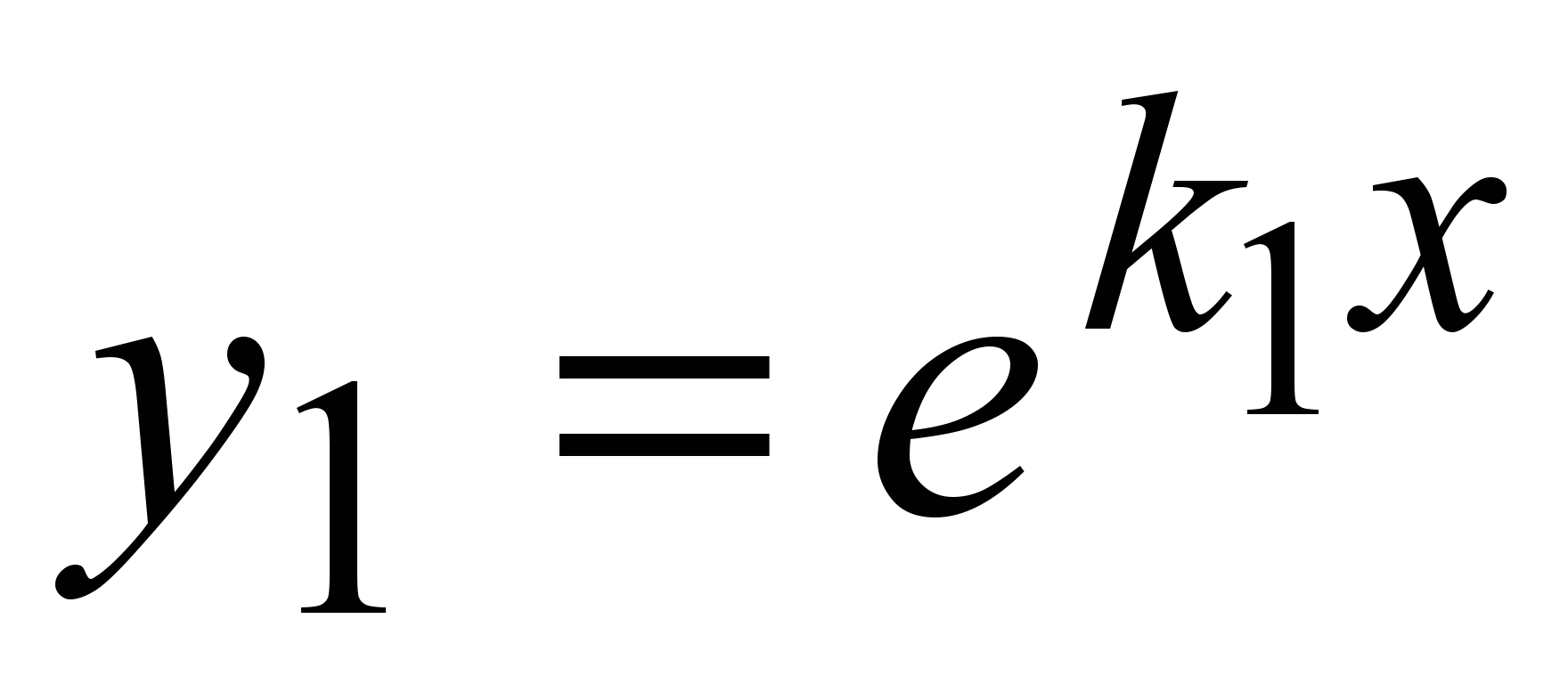 . Покажем, что в этом случае в качестве второго линейно независимого решения можно взять . Покажем, что в этом случае в качестве второго линейно независимого решения можно взять 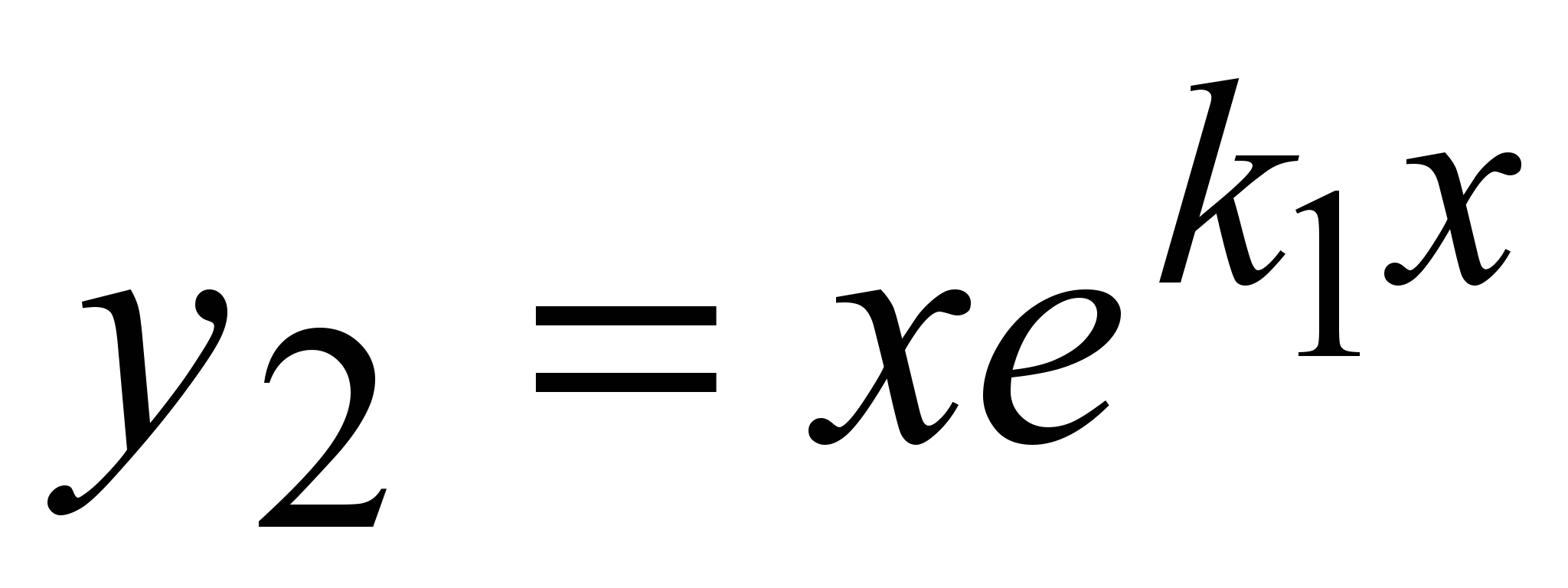 . Подставим его в уравнение (1). Сначала найдём производные: . Подставим его в уравнение (1). Сначала найдём производные:
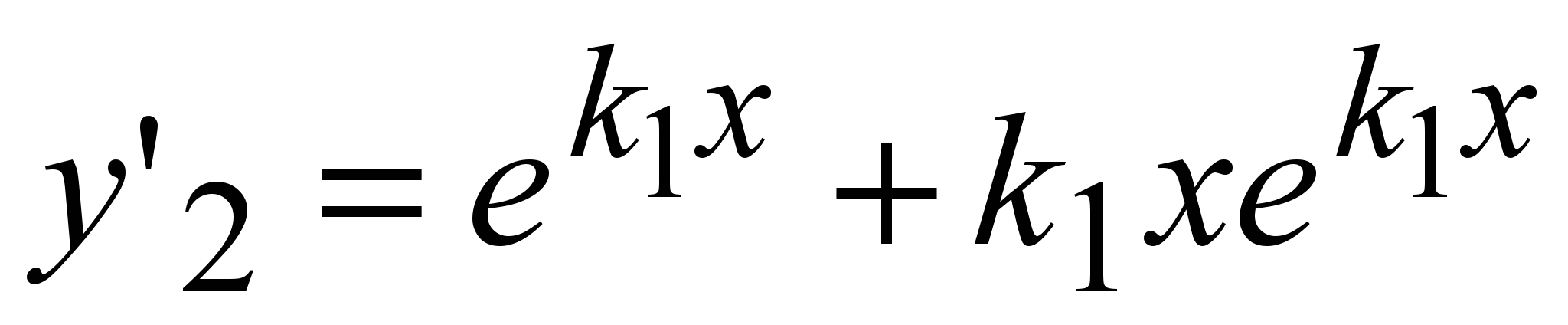 ; ; 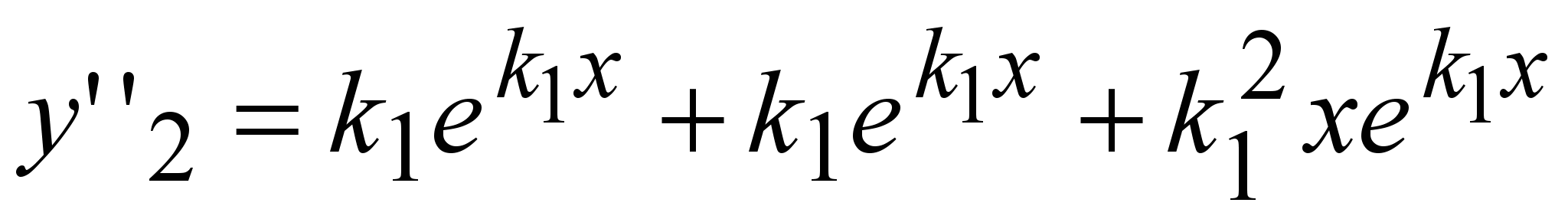
Подставим в (1):
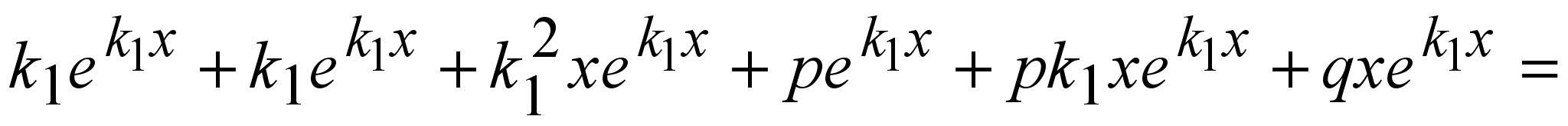
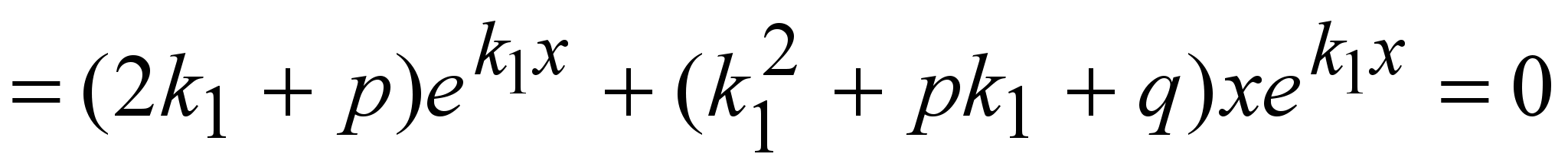 , т.к. , т.к.
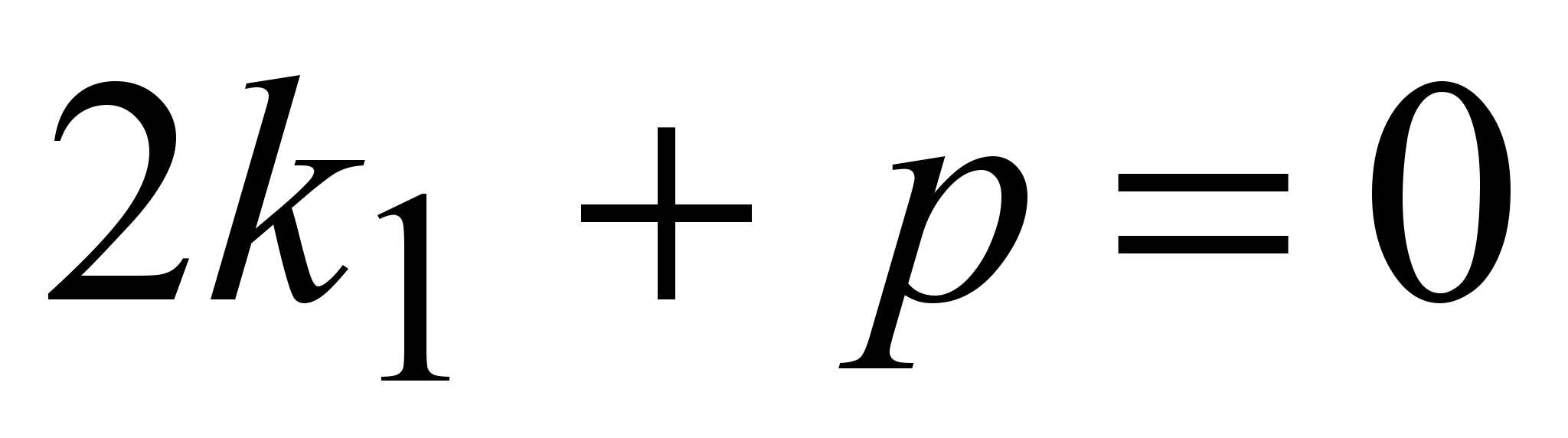 и и 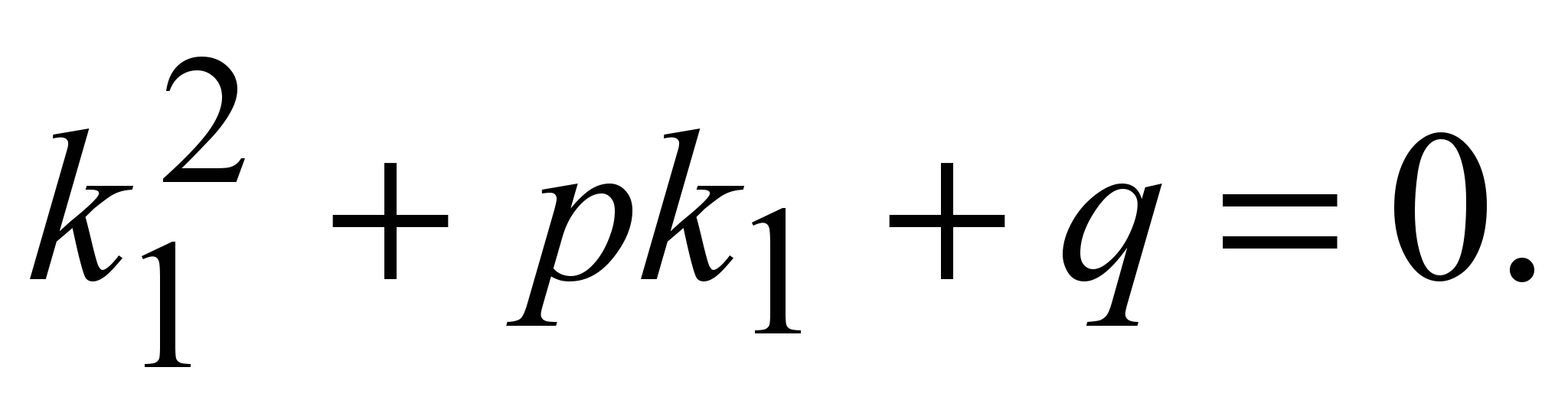
Итак, в случае 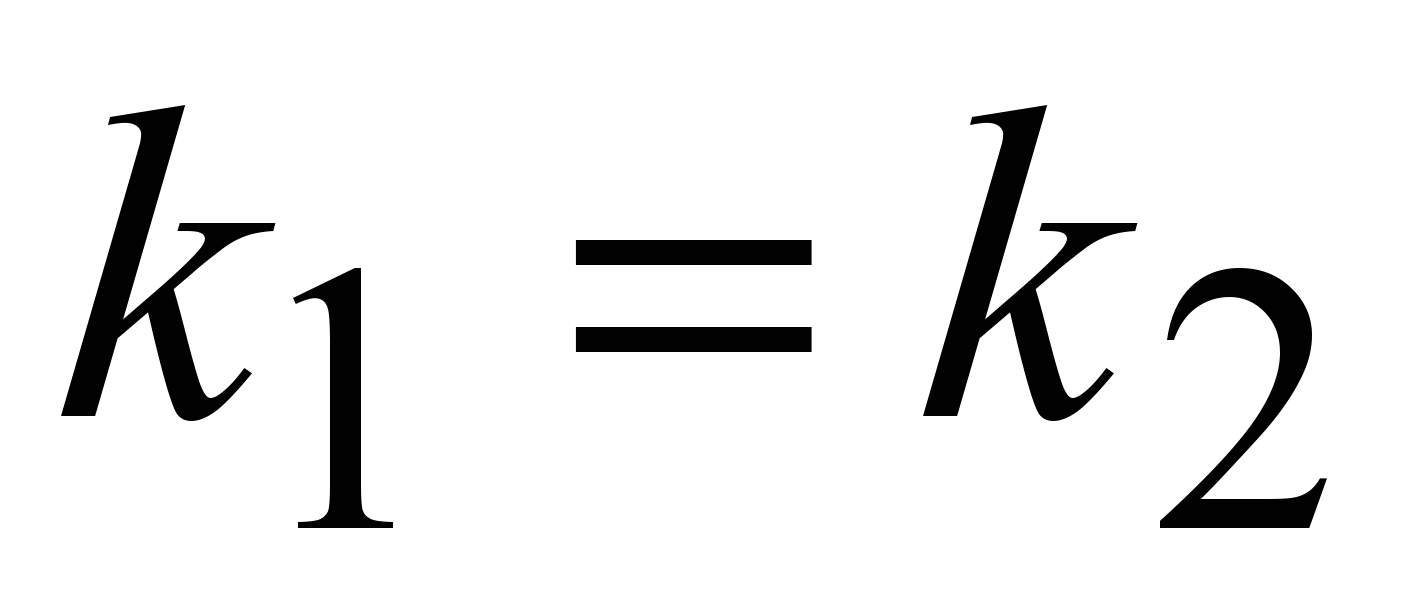 общее решение уравнения (1) имеет вид общее решение уравнения (1) имеет вид
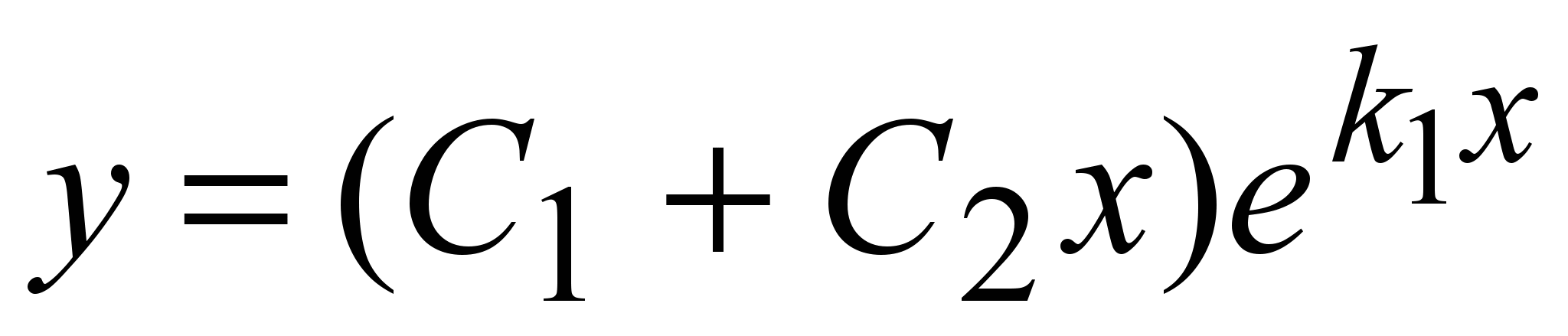 (8) (8)
IІI. Корни характеристического уравнения комплексные
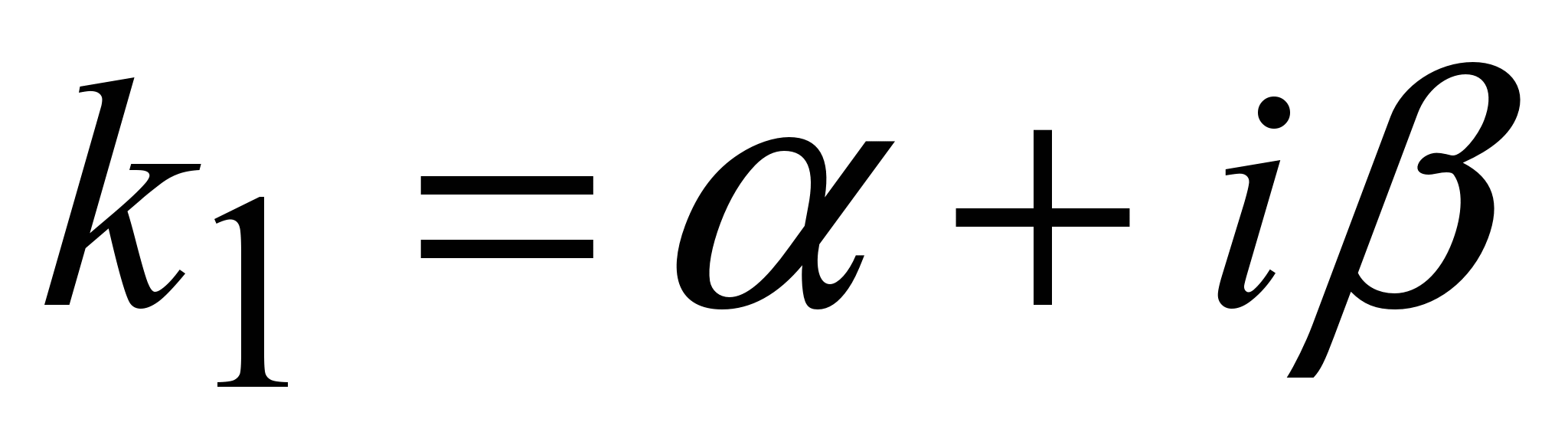 ; ; 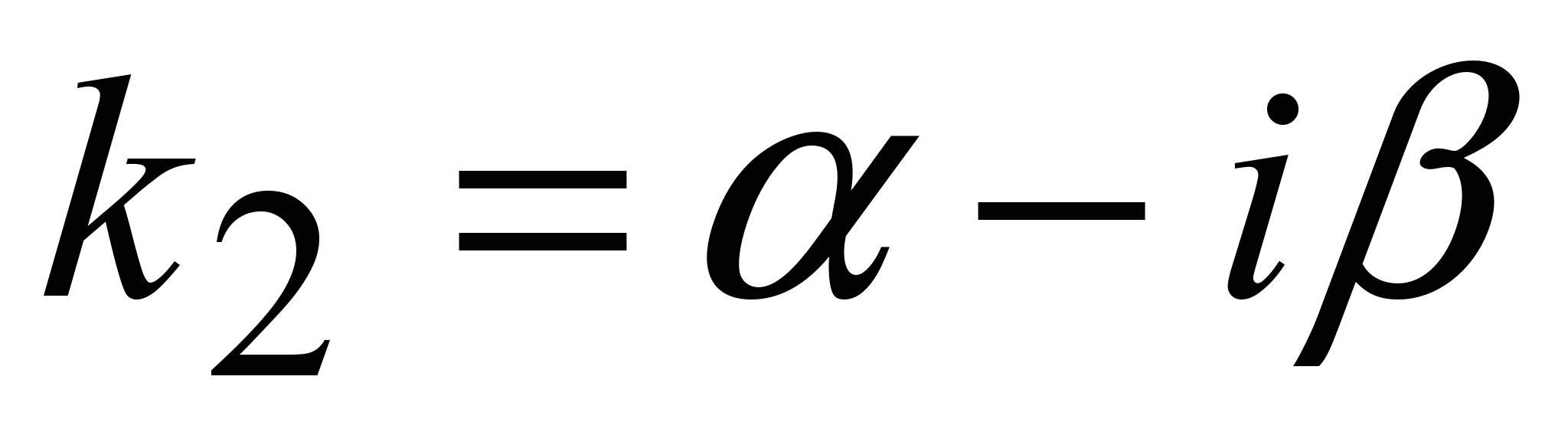 , ( , (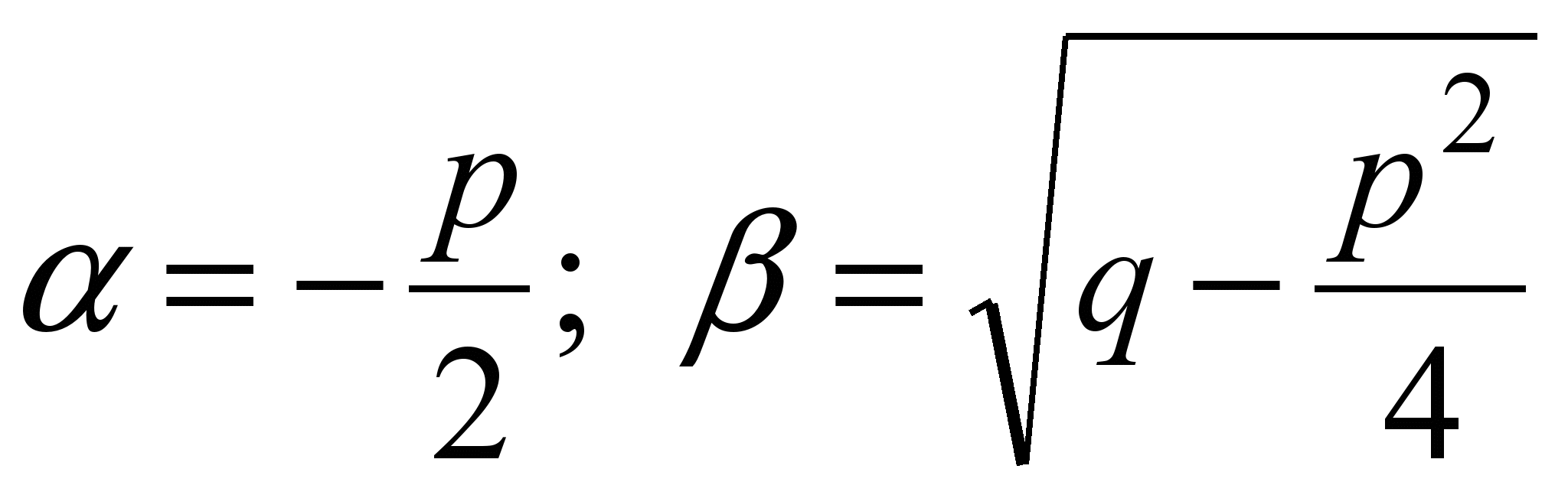 ). ).
Частные решения: 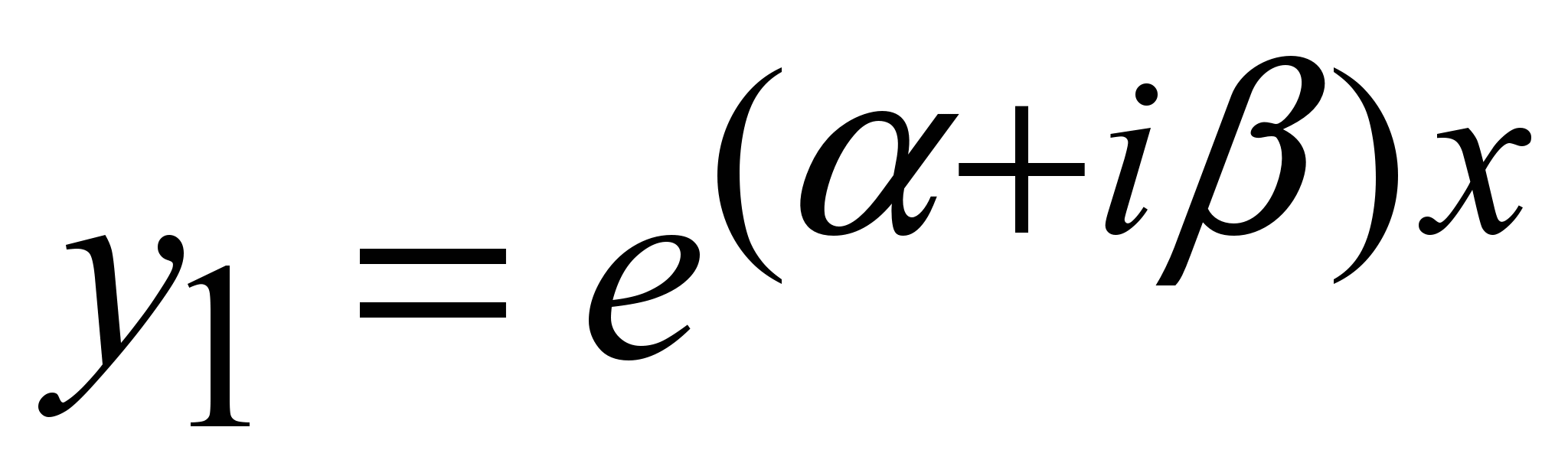 ; ; 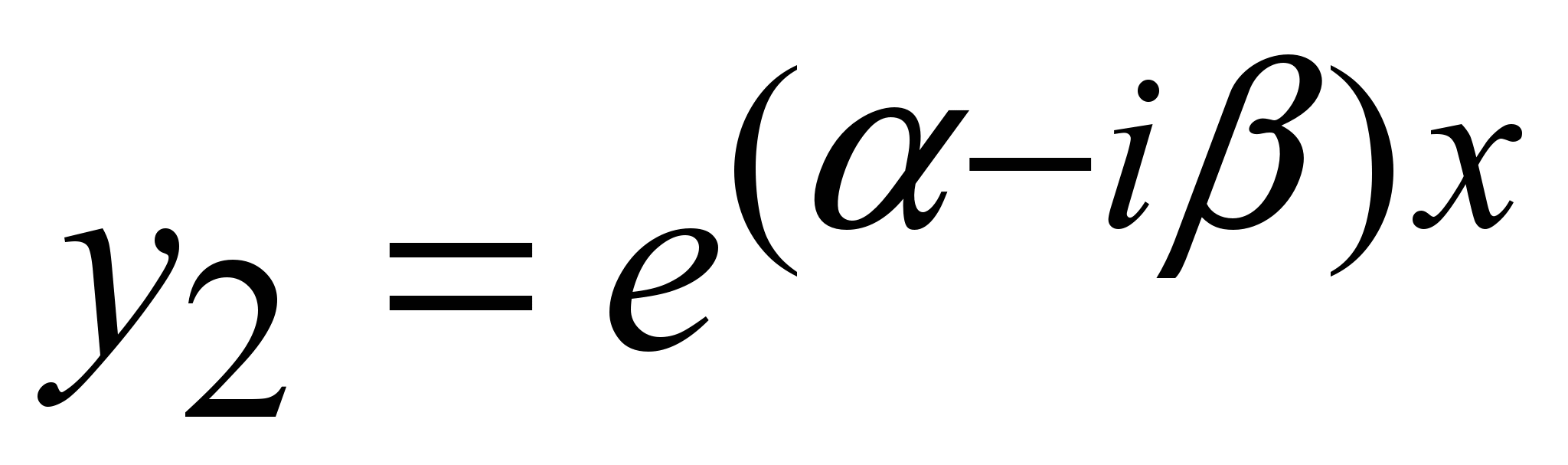 , или , или
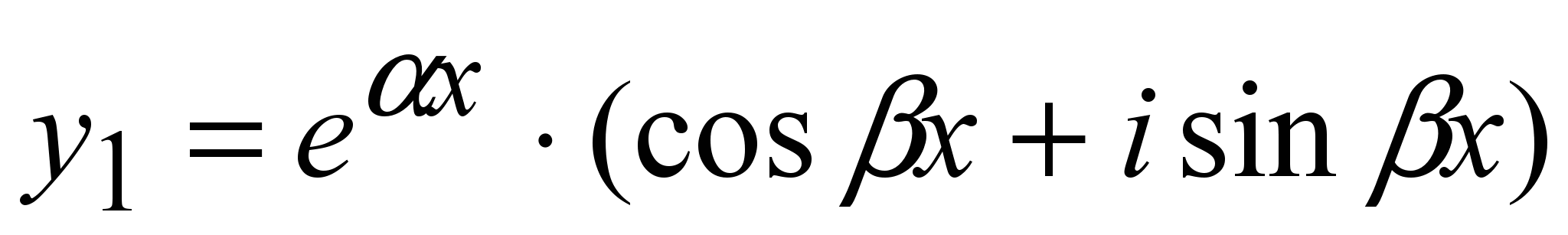 ; ; 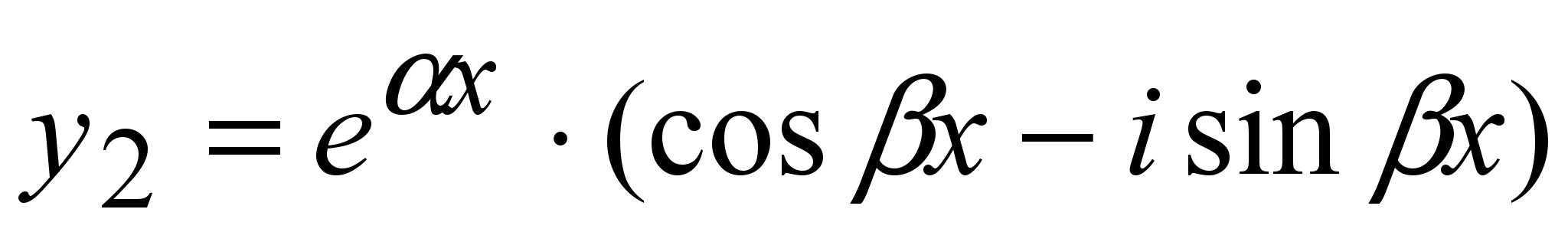 (5) (5)
Покажем, что если некоторая комплексная функция 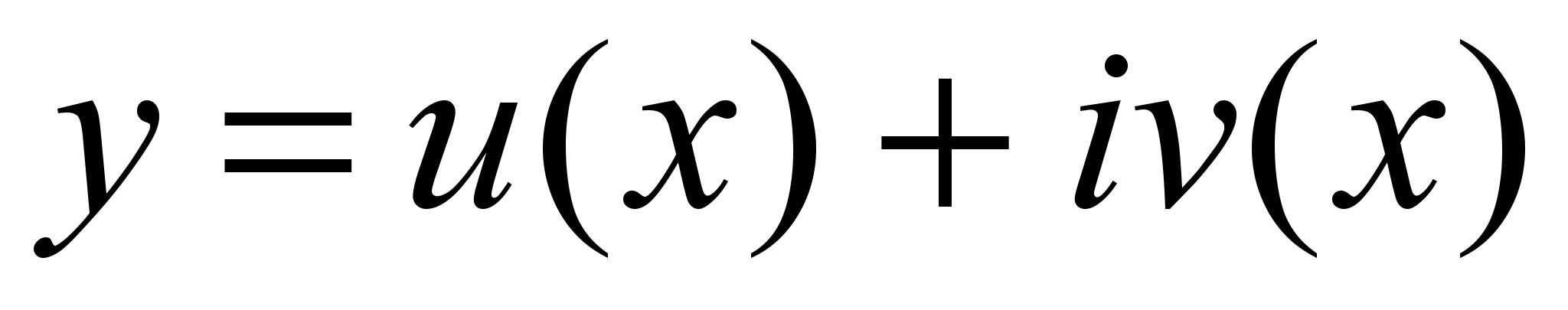 является решением уравнения (1), то каждая из действительных функций u(x) и v(x) тоже будет решением уравнения (1). для этого подставим его в уравнение (1): является решением уравнения (1), то каждая из действительных функций u(x) и v(x) тоже будет решением уравнения (1). для этого подставим его в уравнение (1):
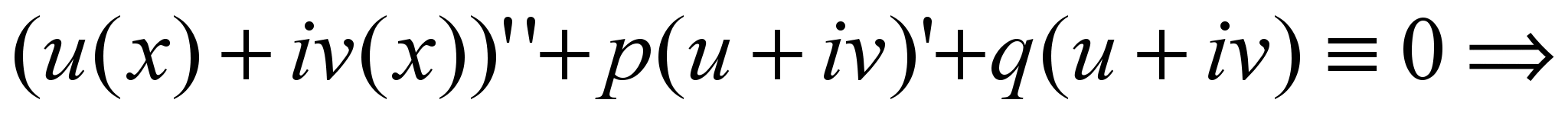
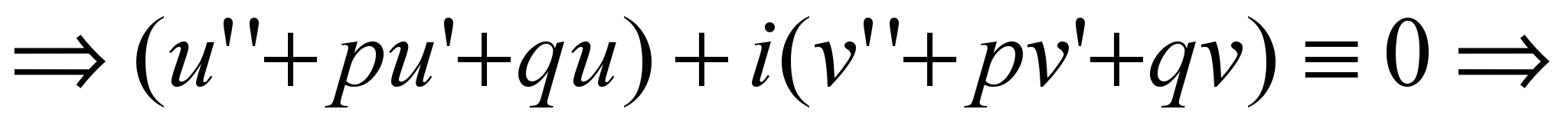 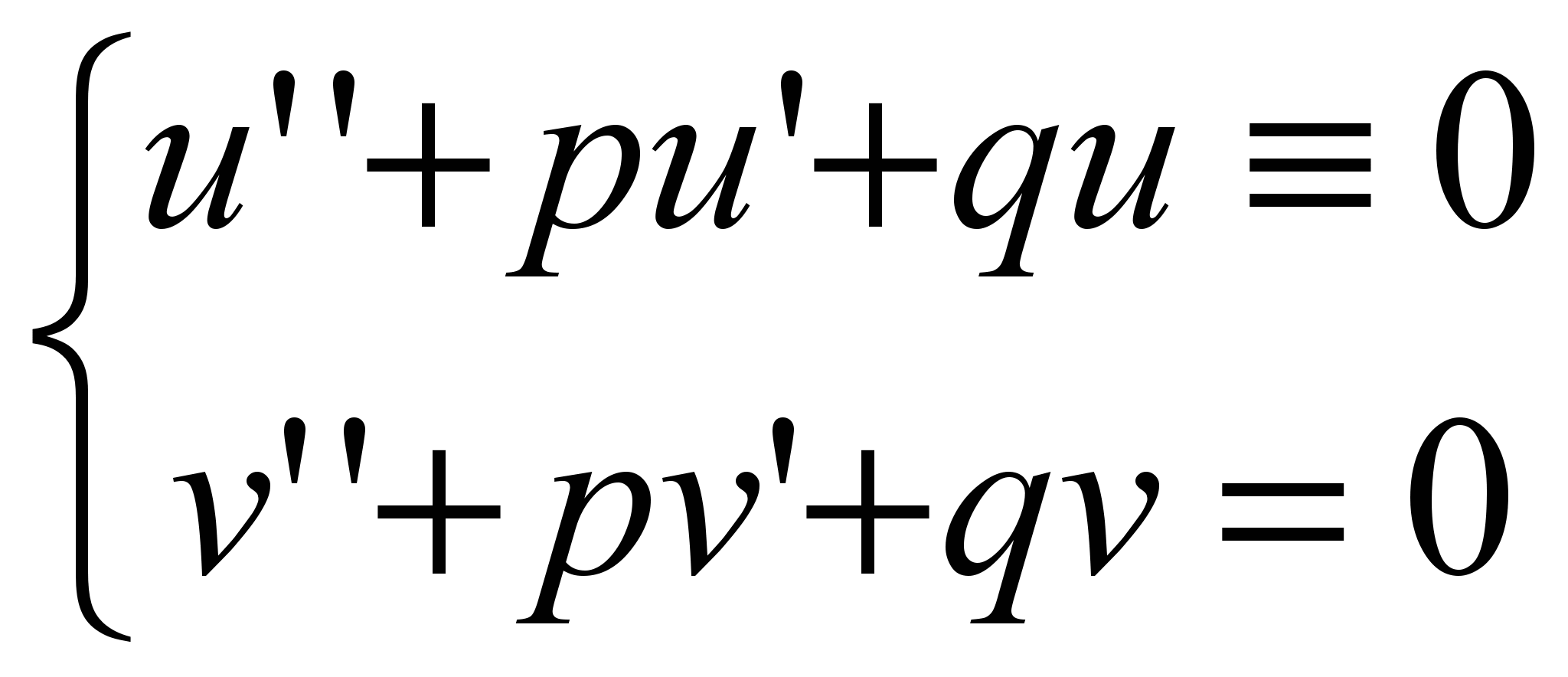 . .
Значит, в качестве частных решений уравнения (1) можно взять отдельно действительные и мнимые части решений (5):
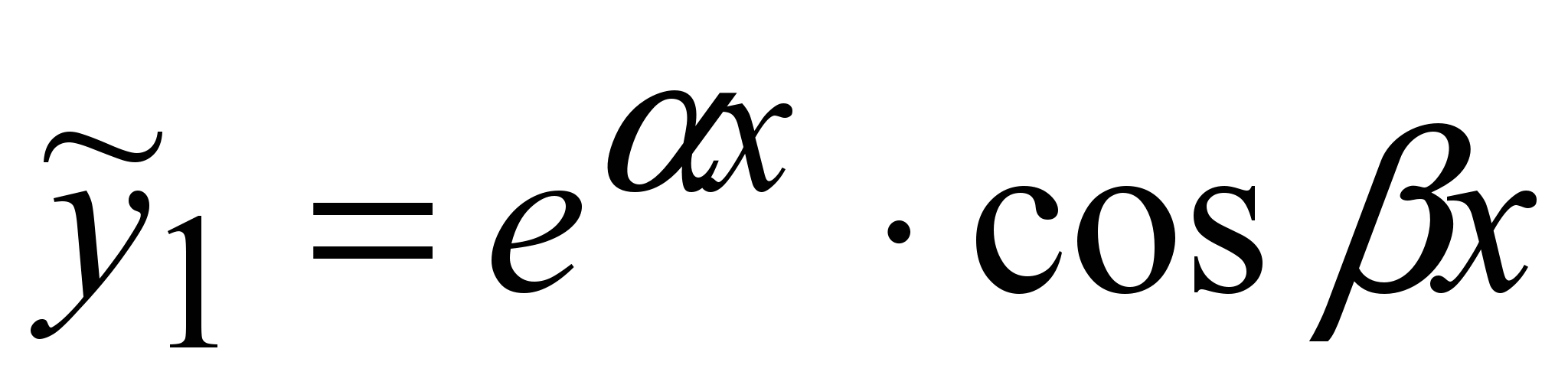 ; ; 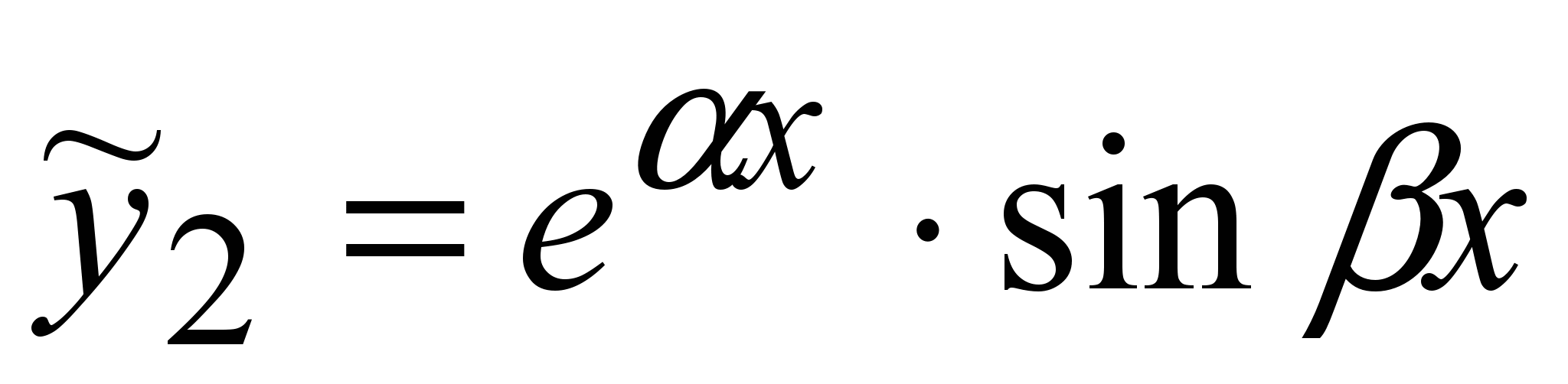 , ,
В этом случае общее решение уравнения (1) можно представить в виде
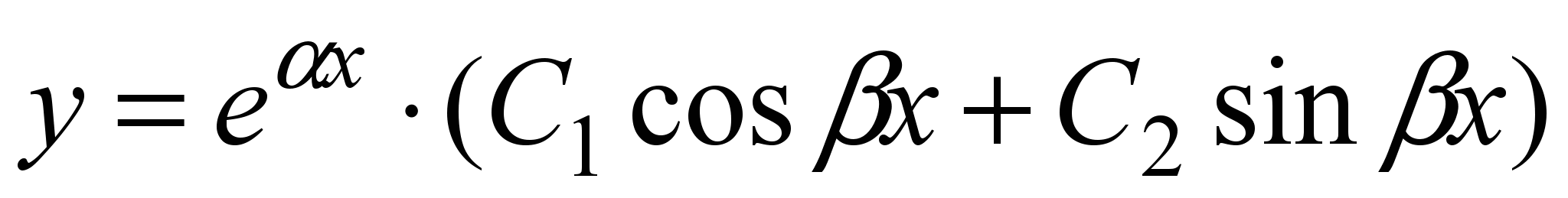 , (6) , (6)
где 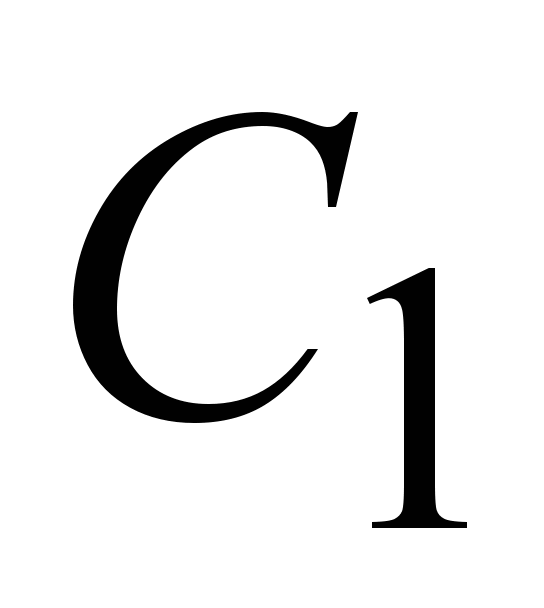 и и 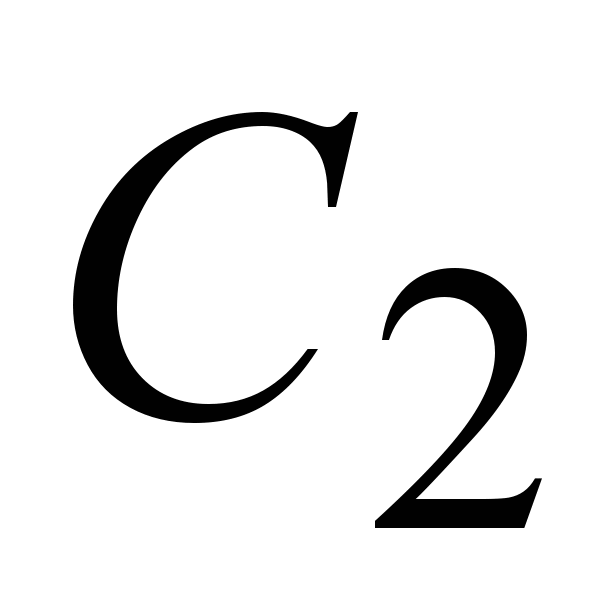 -произвольные постоянные. -произвольные постоянные.
Важным частным случаем решения (6) является случай, когда в уравнении (1) p=0 и q
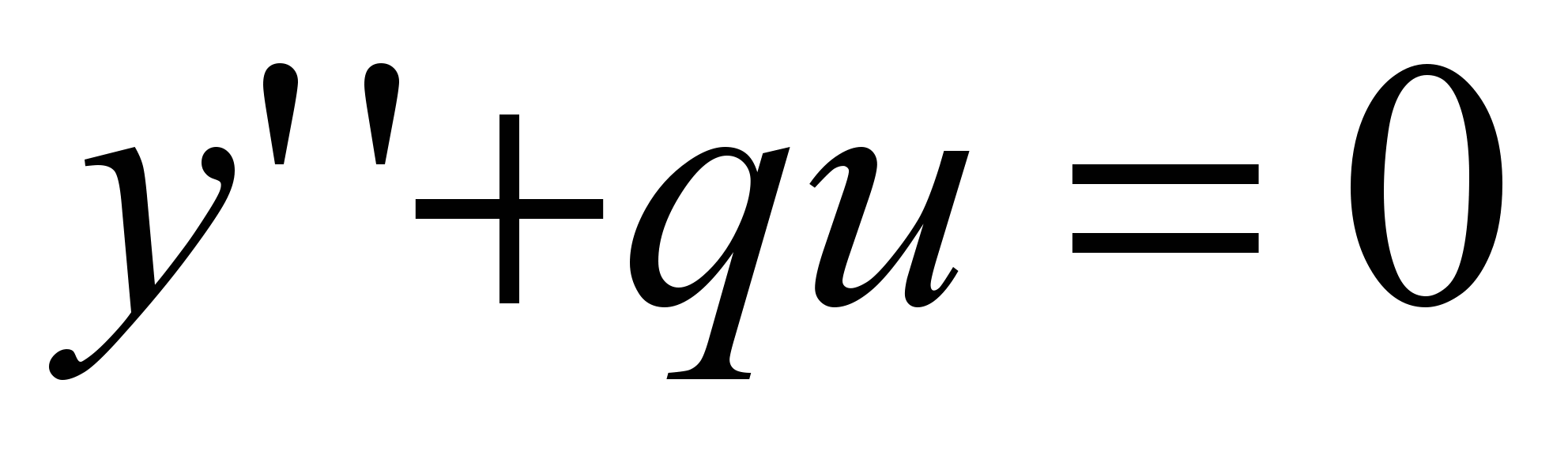 , (q , (q
При этом характеристическое уравнение 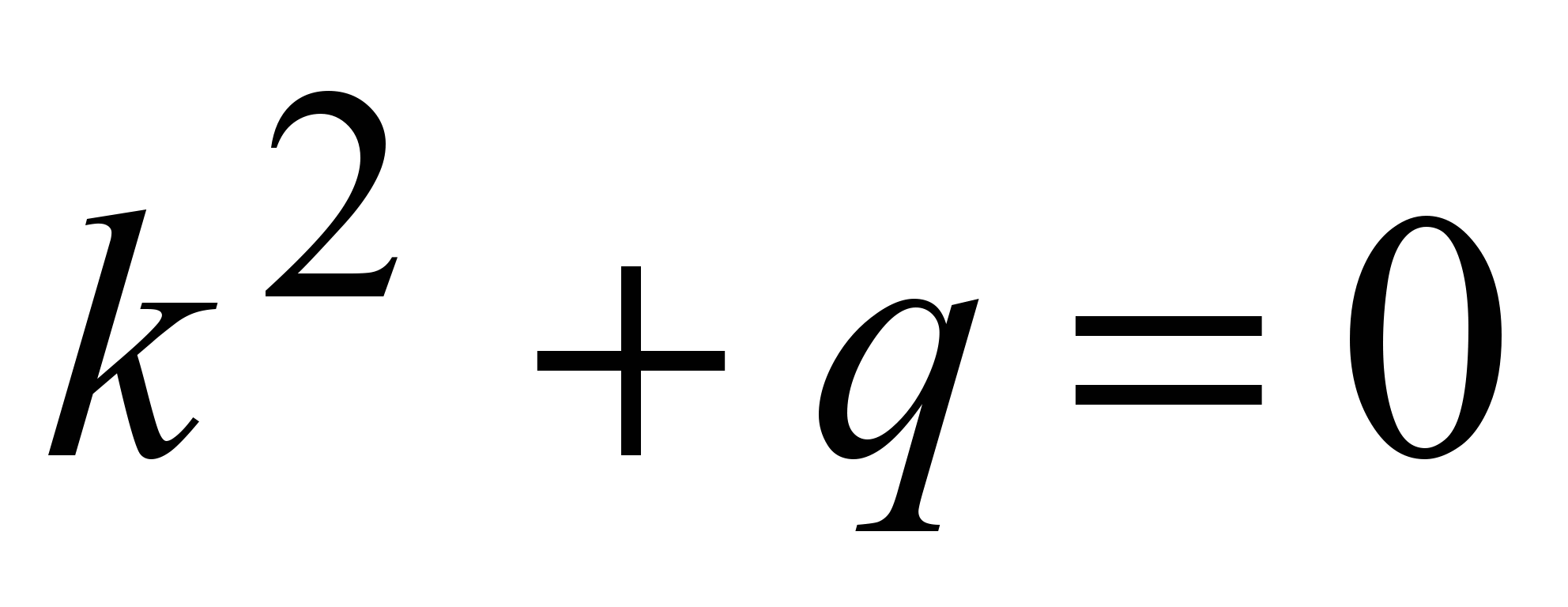 (q (q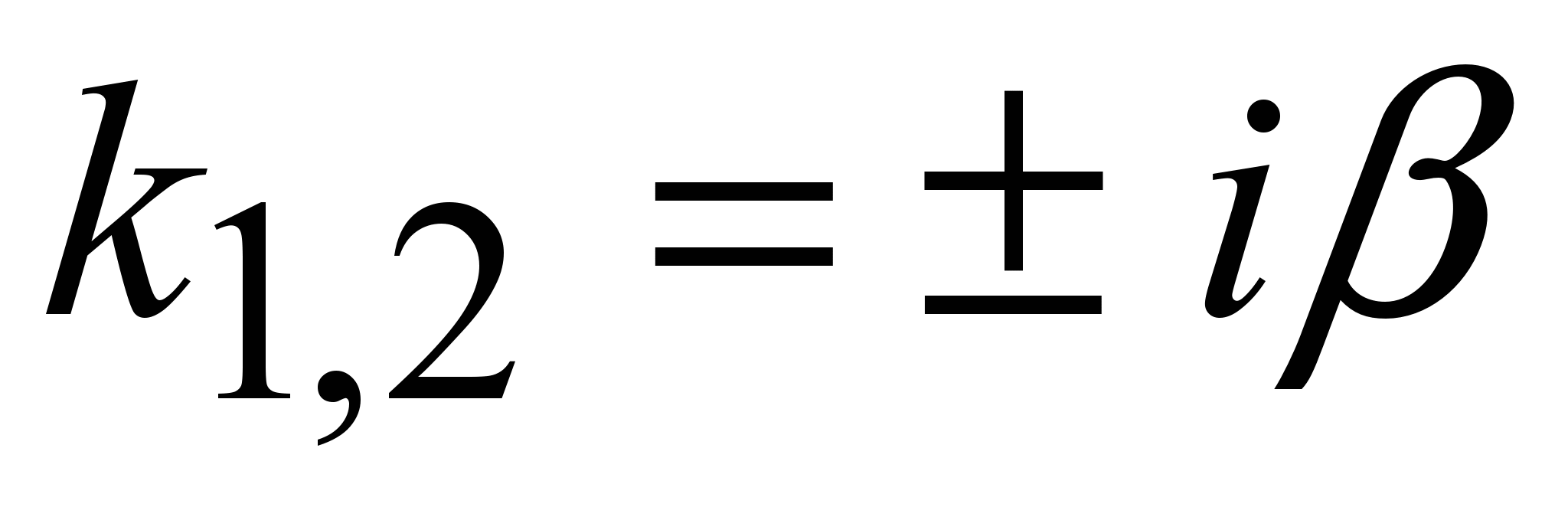 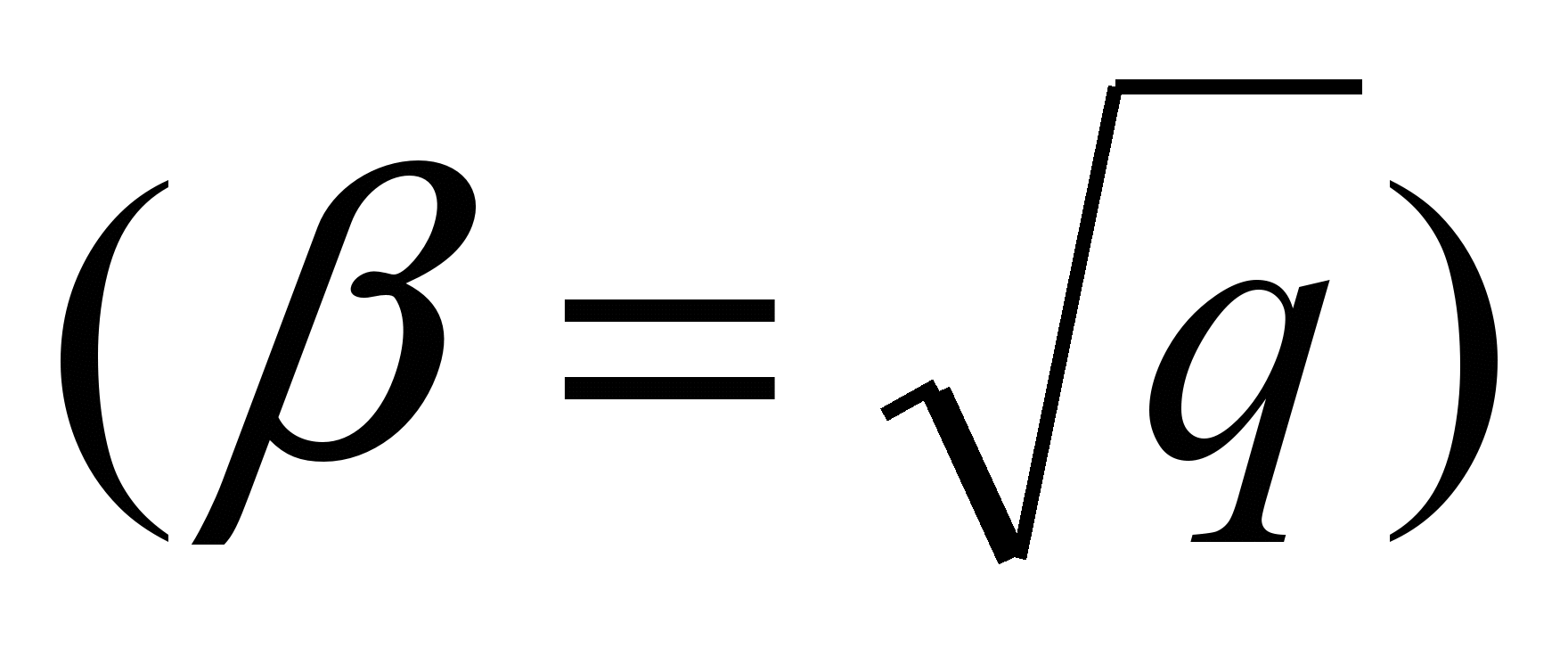 и общее решение (6) приобретает вид и общее решение (6) приобретает вид
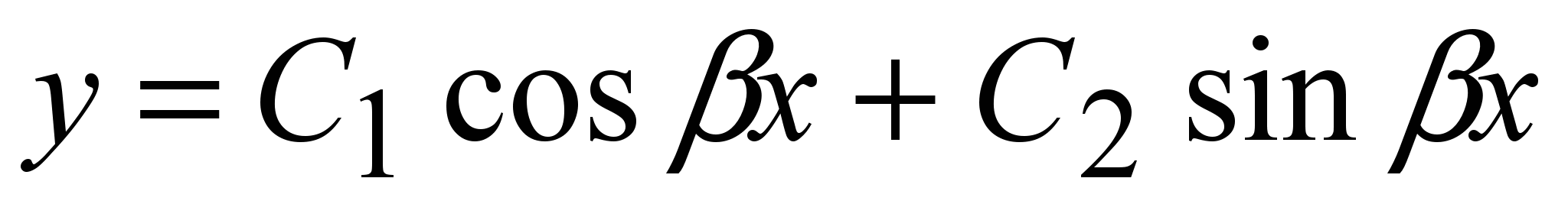 (7) (7)
Примеры:
Найти общее решение линейных однородных дифференциальных уравнений с постоянными коэффициентами.
1)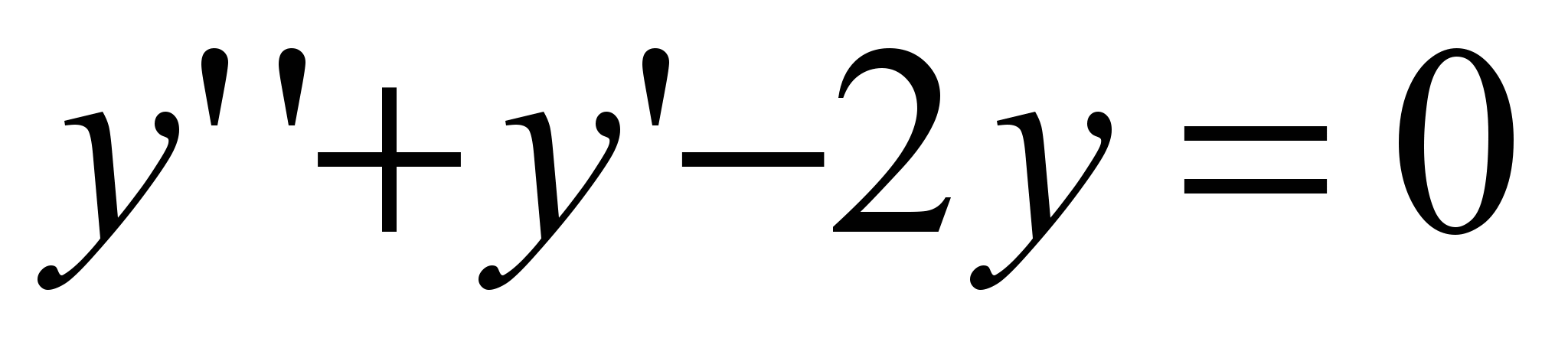
Характеристическое уравнение: 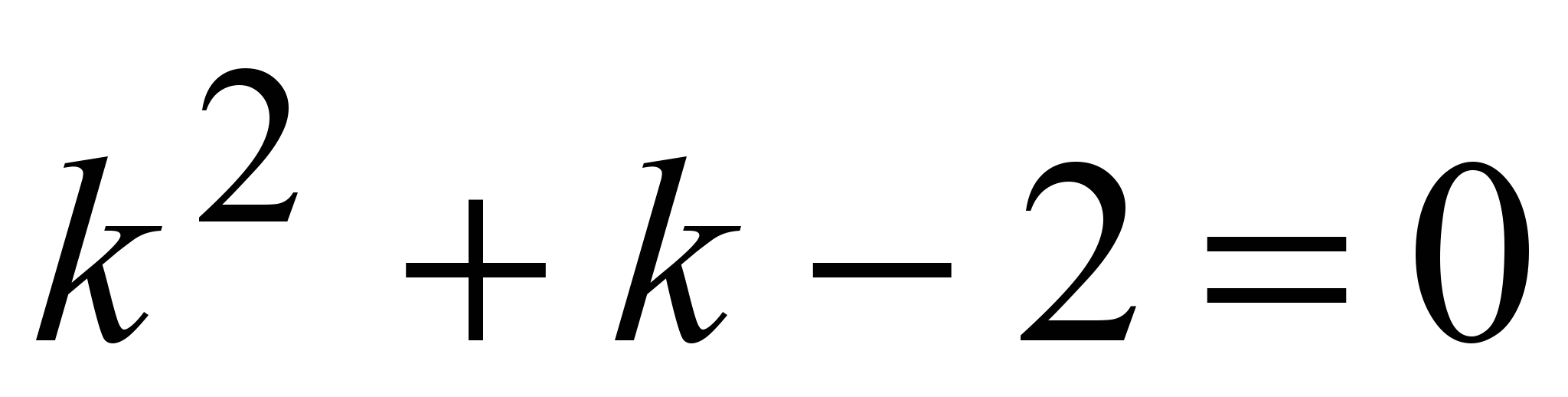 ; ; 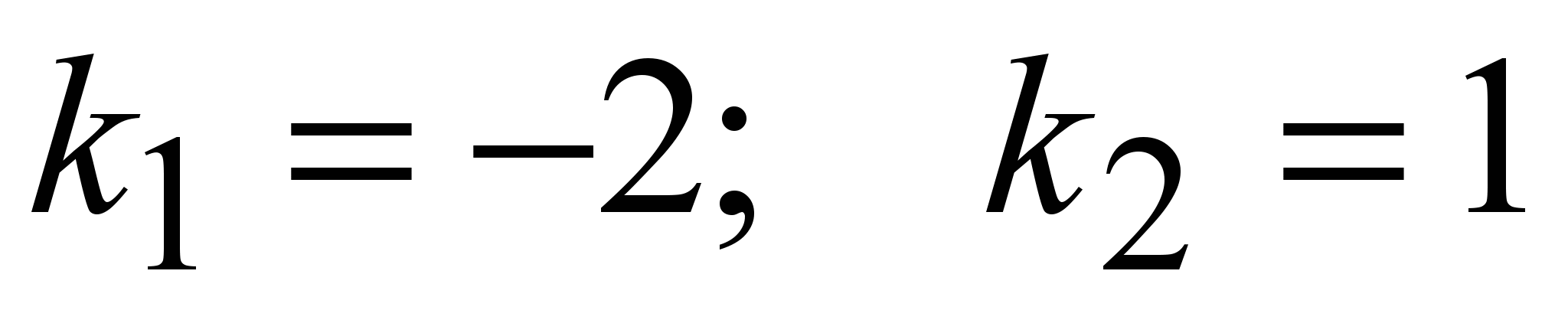 . Имеем первый случай. Общее решение: . Имеем первый случай. Общее решение: 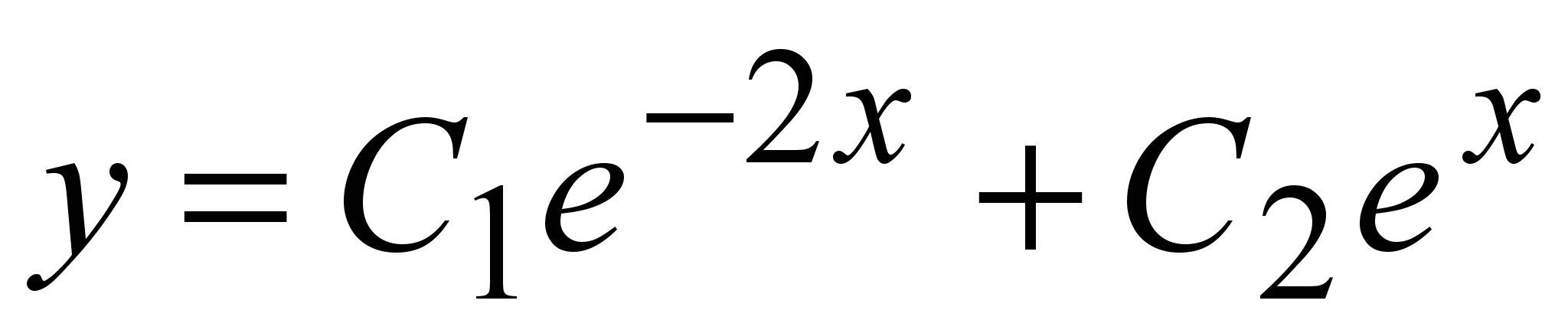
2)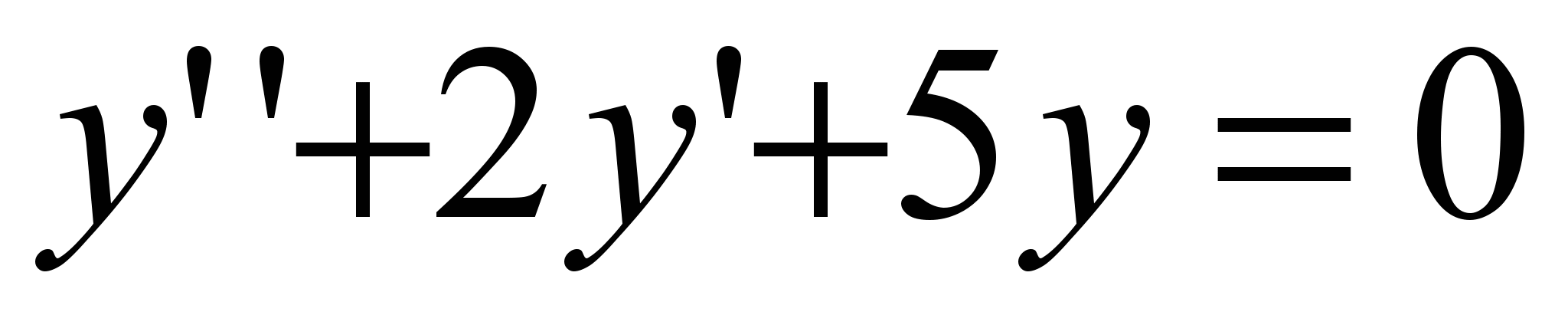 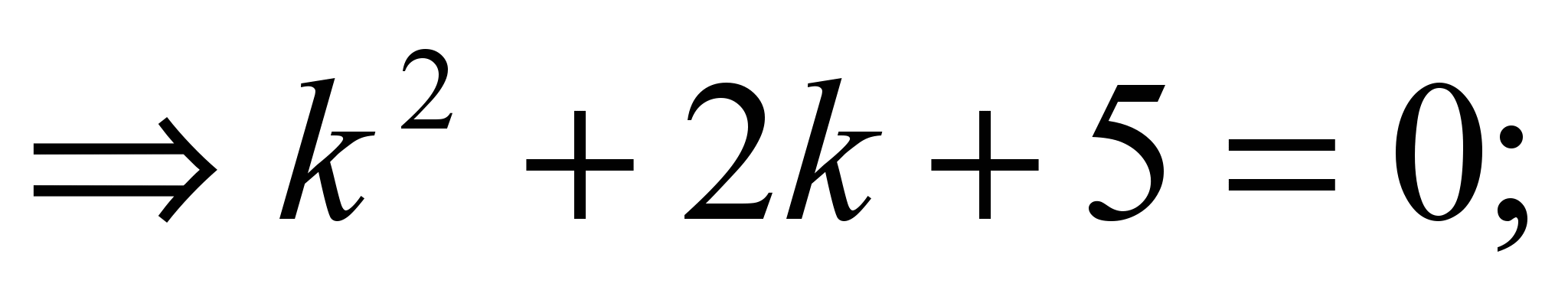 D<0. Второй случай. D<0. Второй случай. 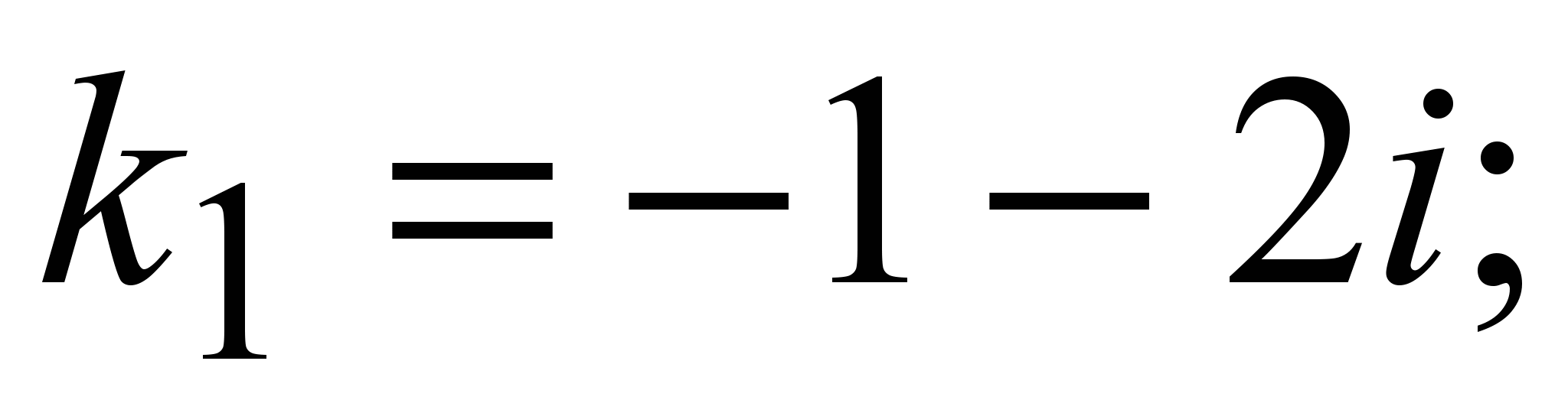 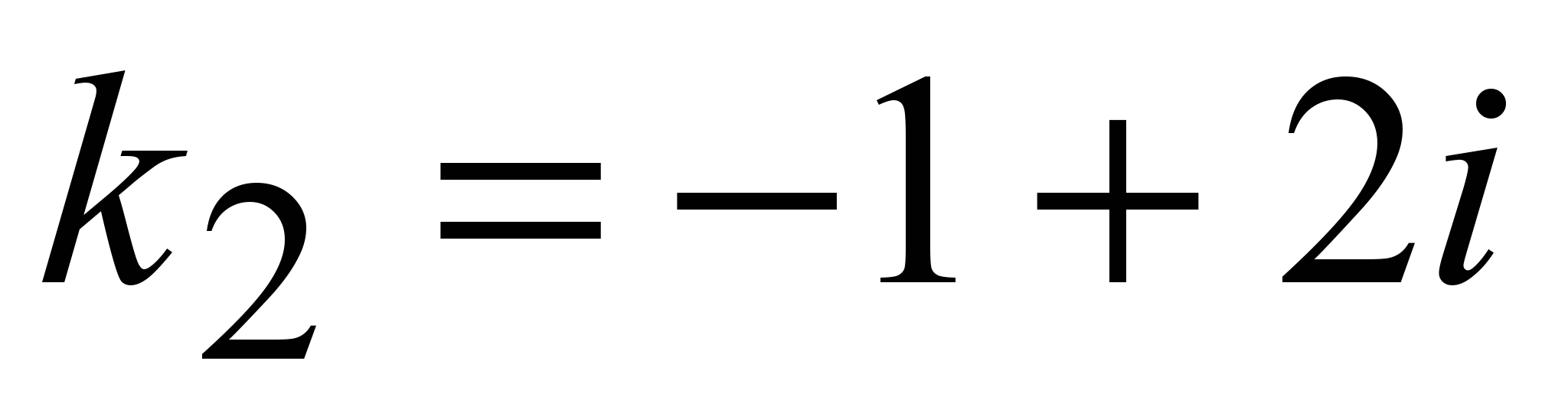
Общее решение: 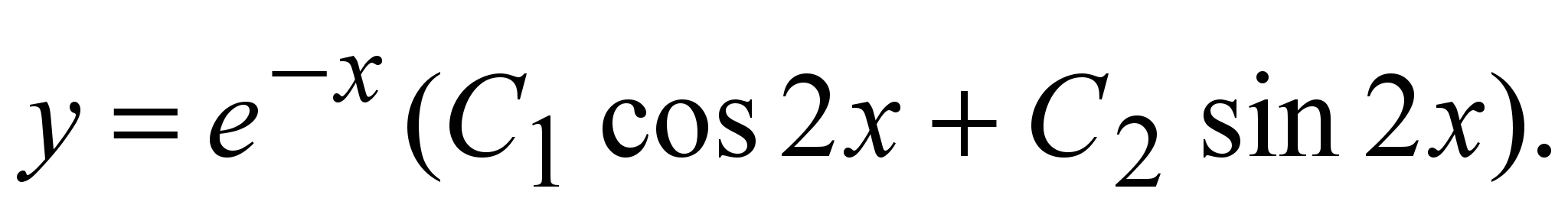
3)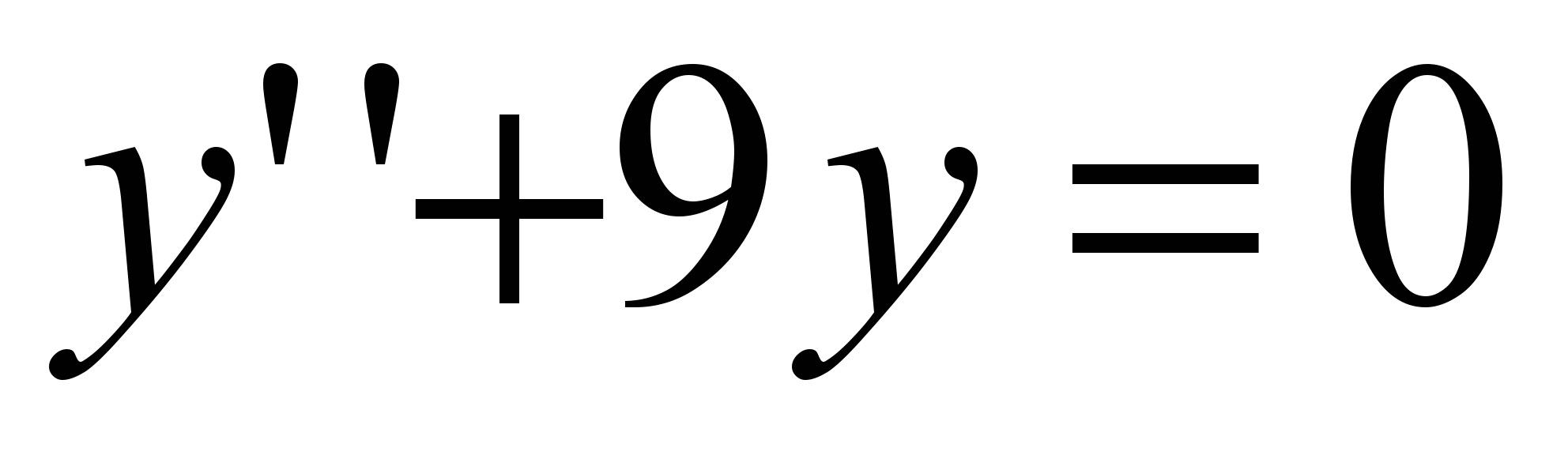 . Случай мнимых корней: . Случай мнимых корней: 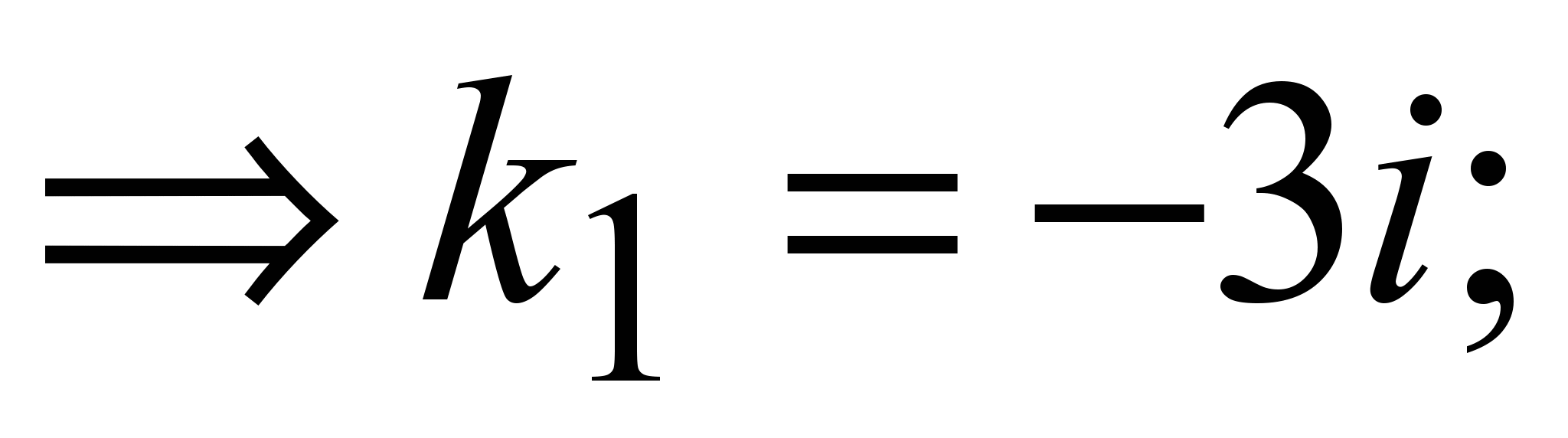 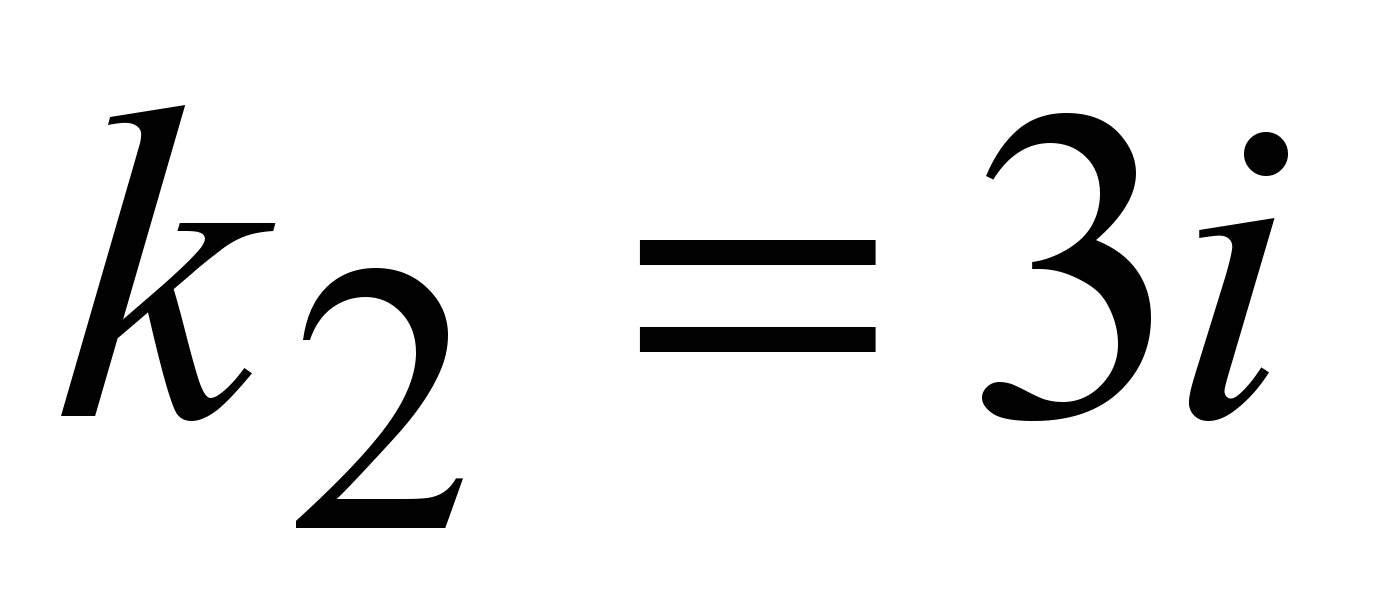
Общее решение: 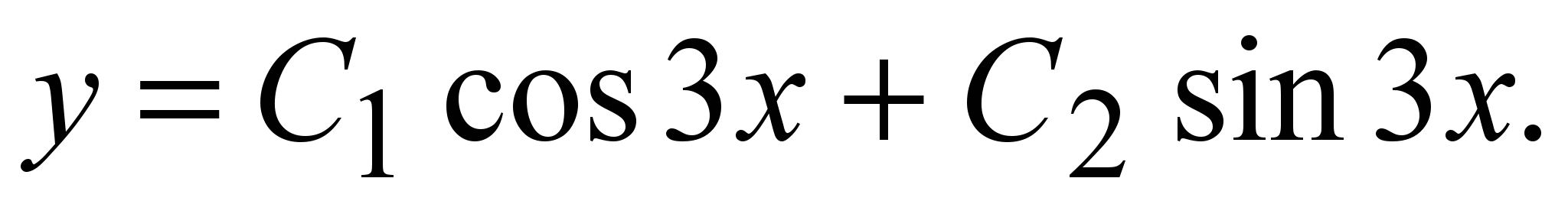
4)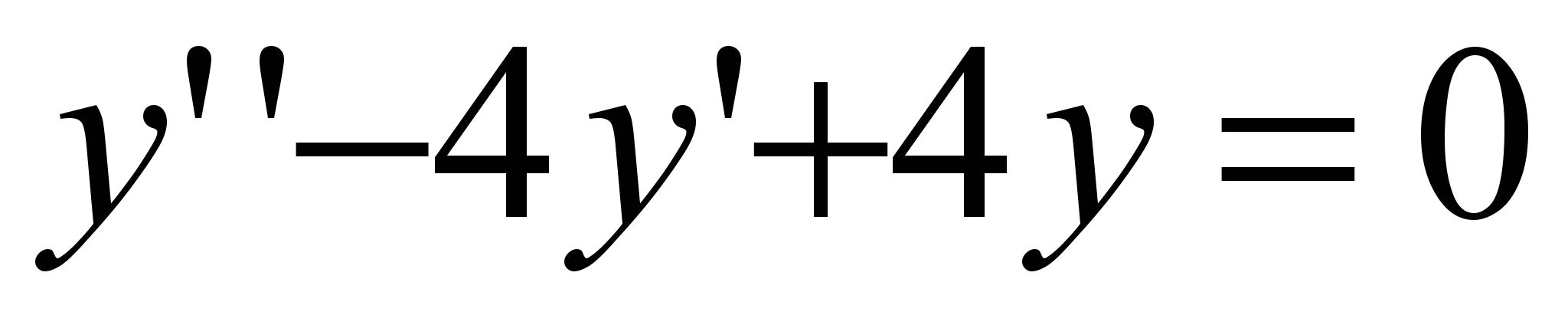 . D=0, третий случай . D=0, третий случай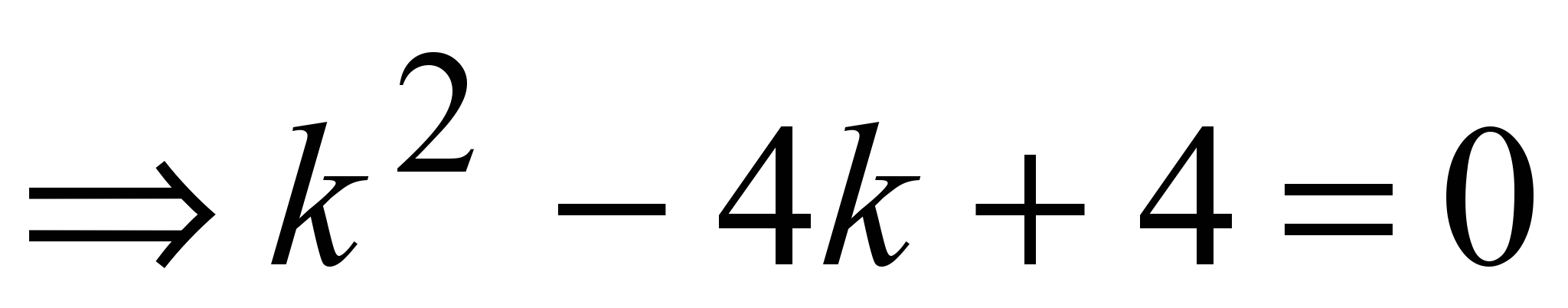 ; ; 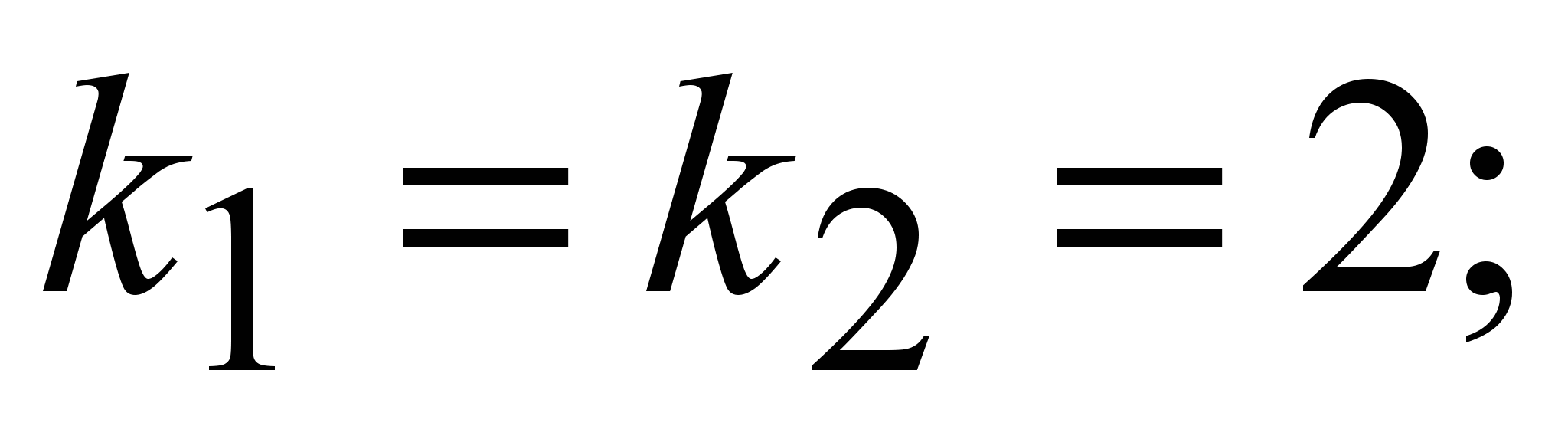
Общее решение: 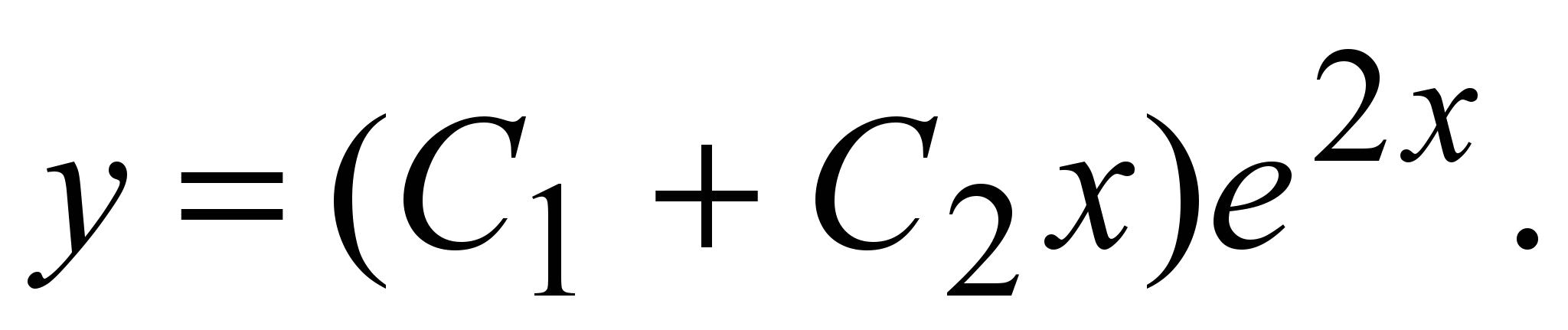
5)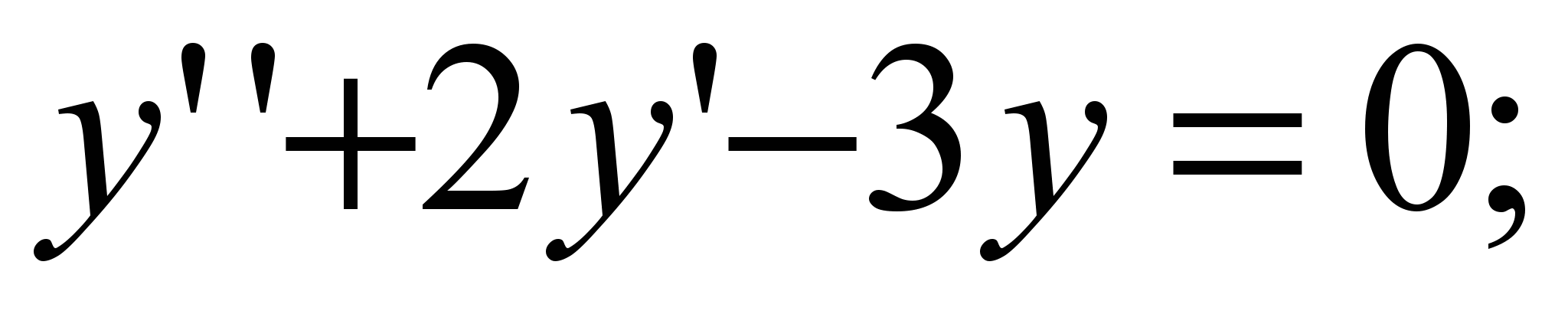 первый случай первый случай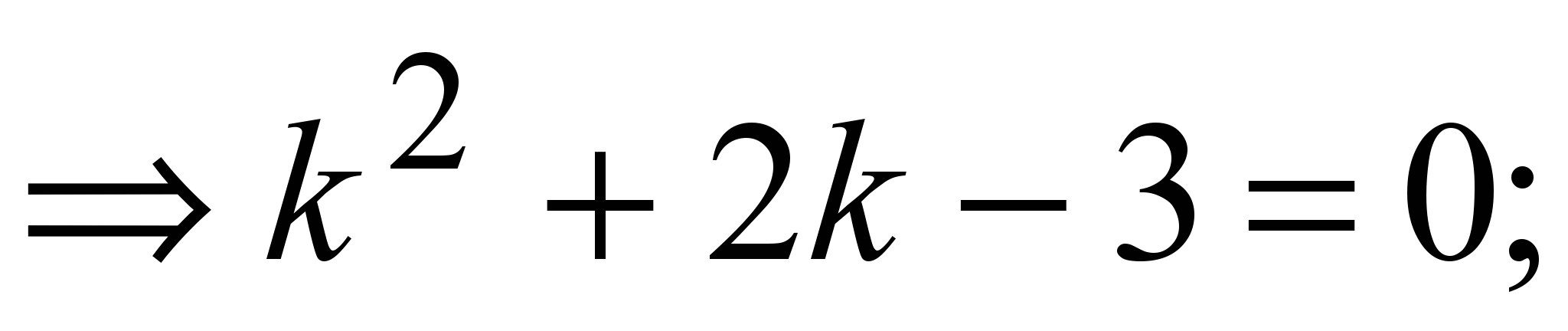 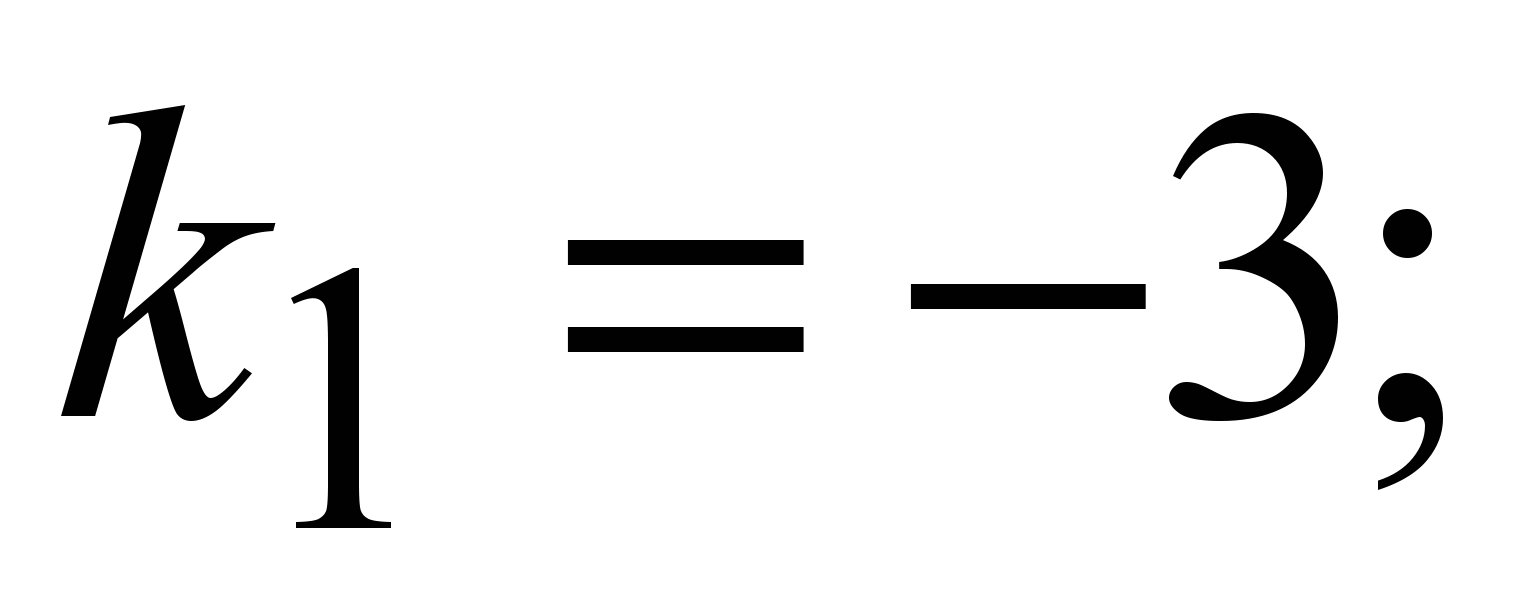 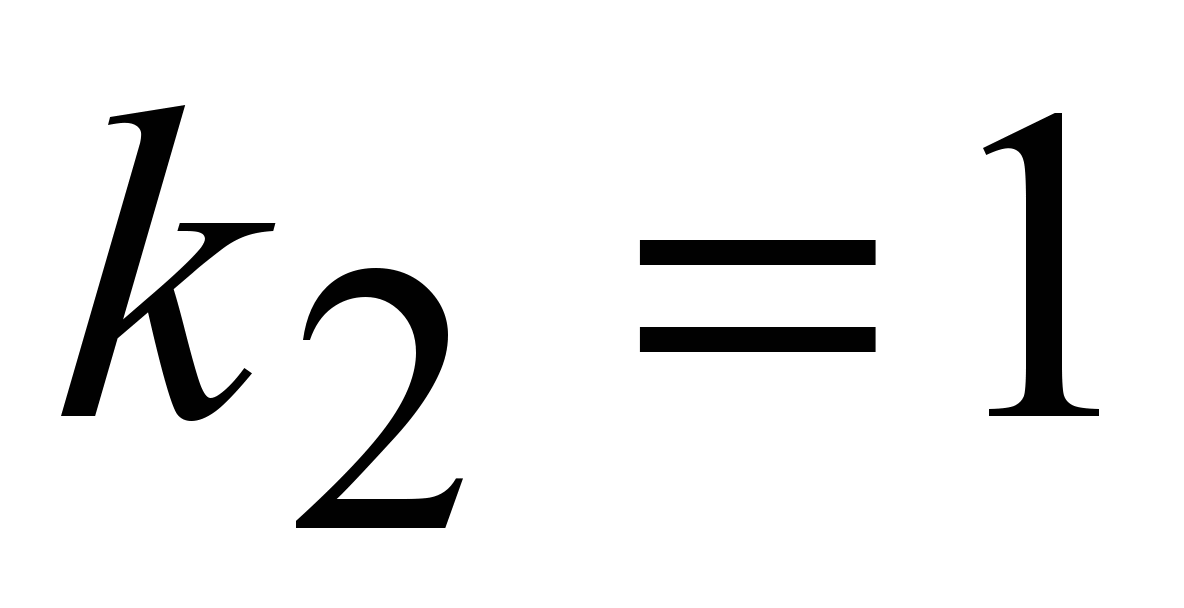
Общее решение: 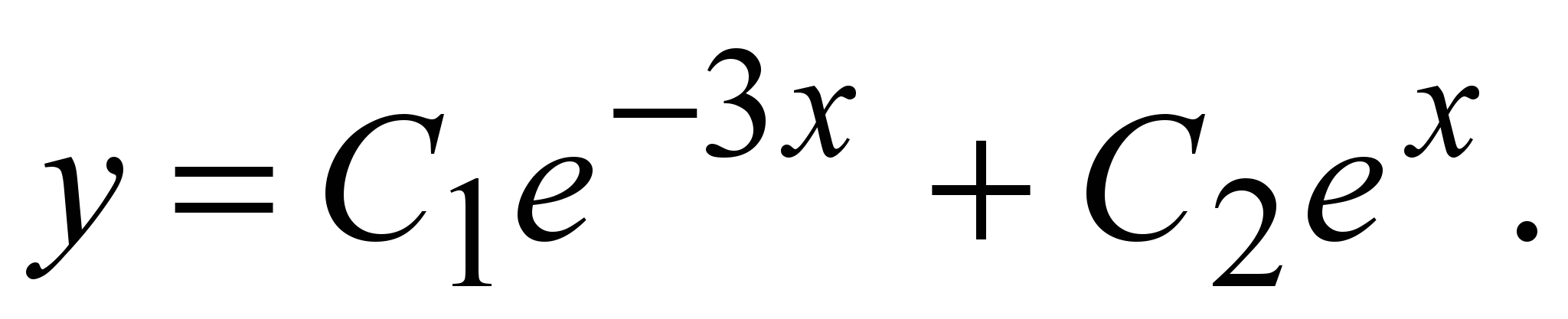
6)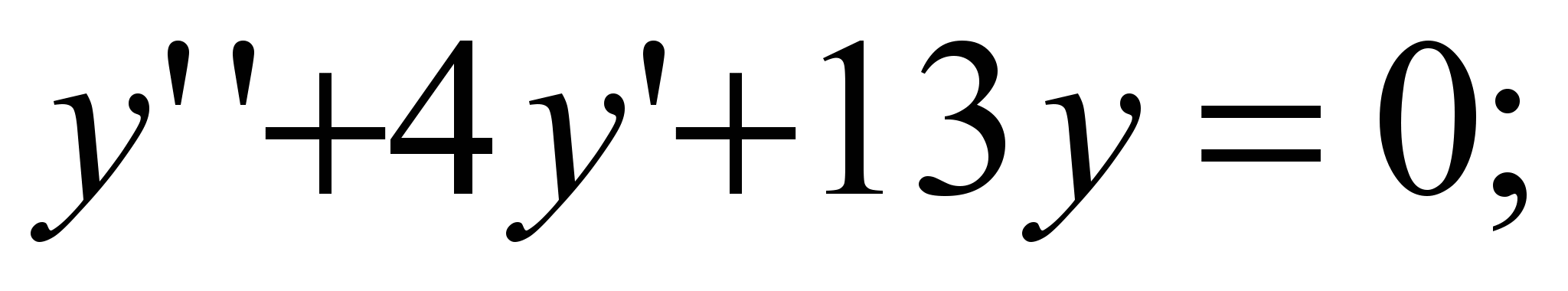 второй случай второй случай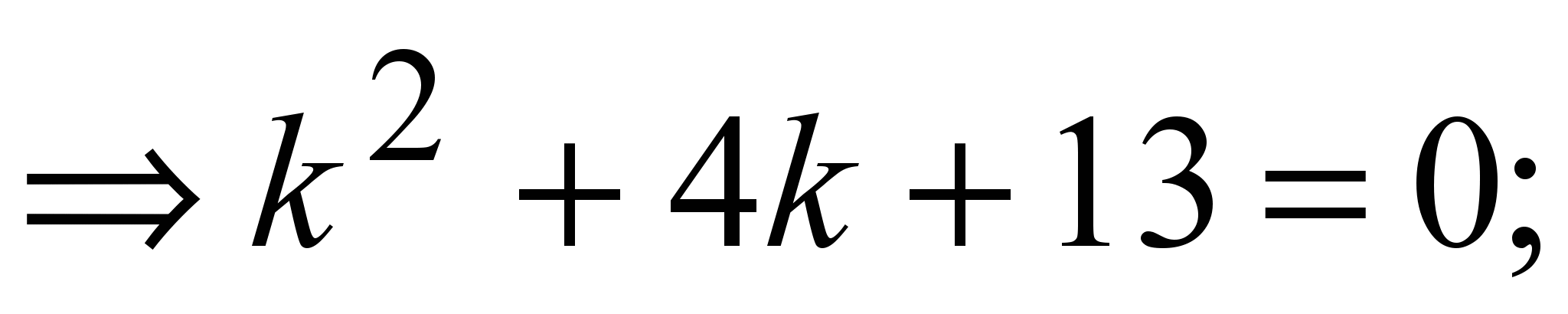 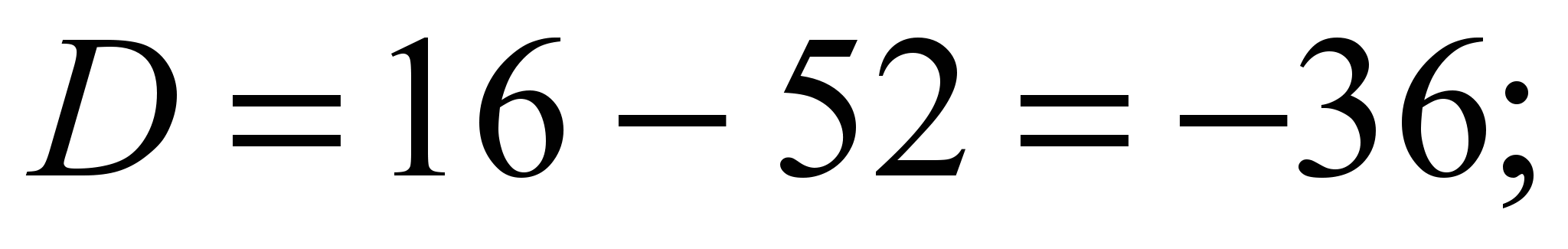 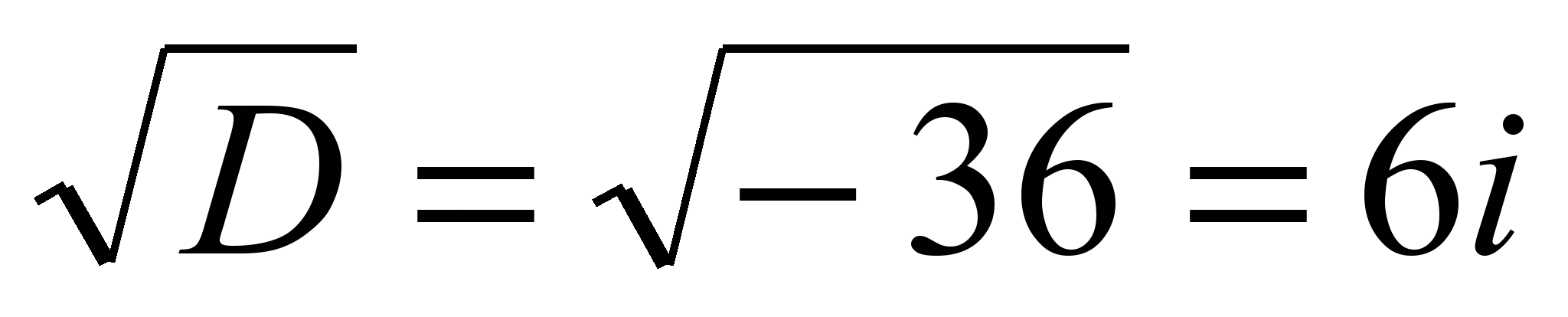 . . 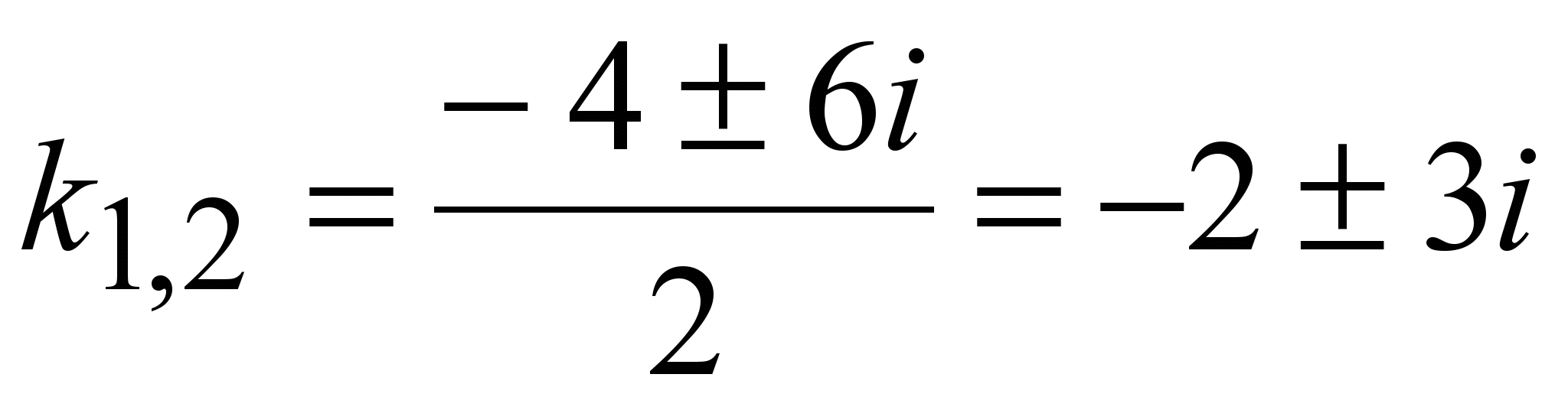 ; ; 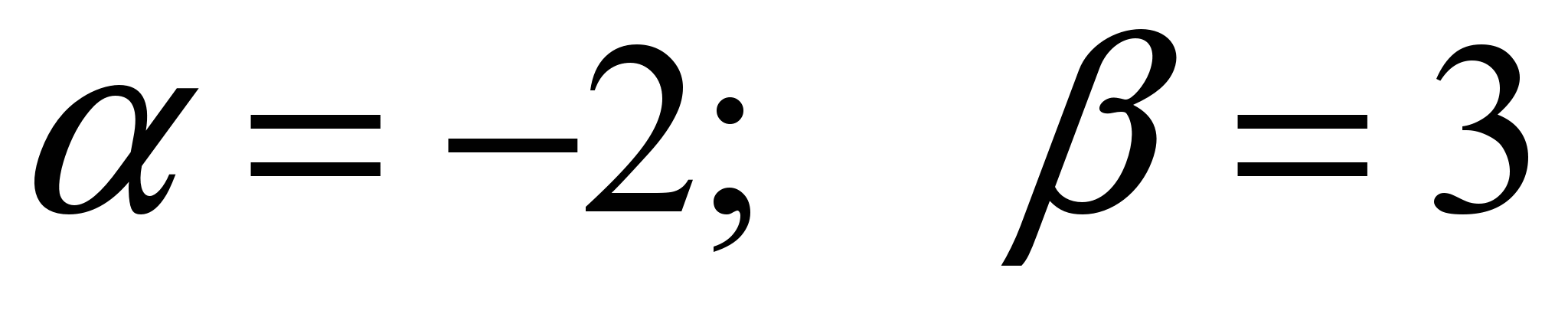 . .
Общее решение: 
7)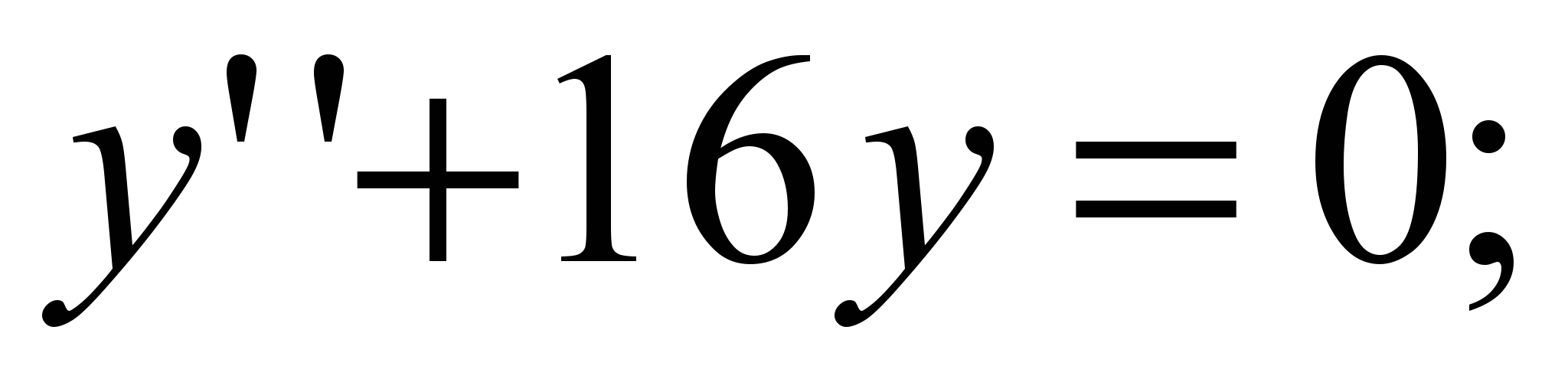 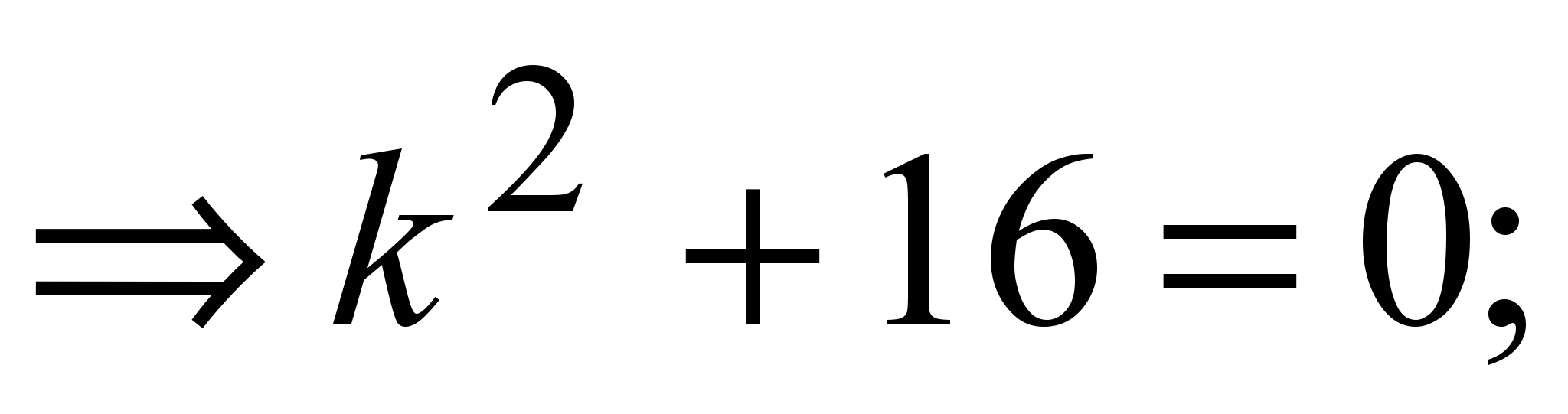 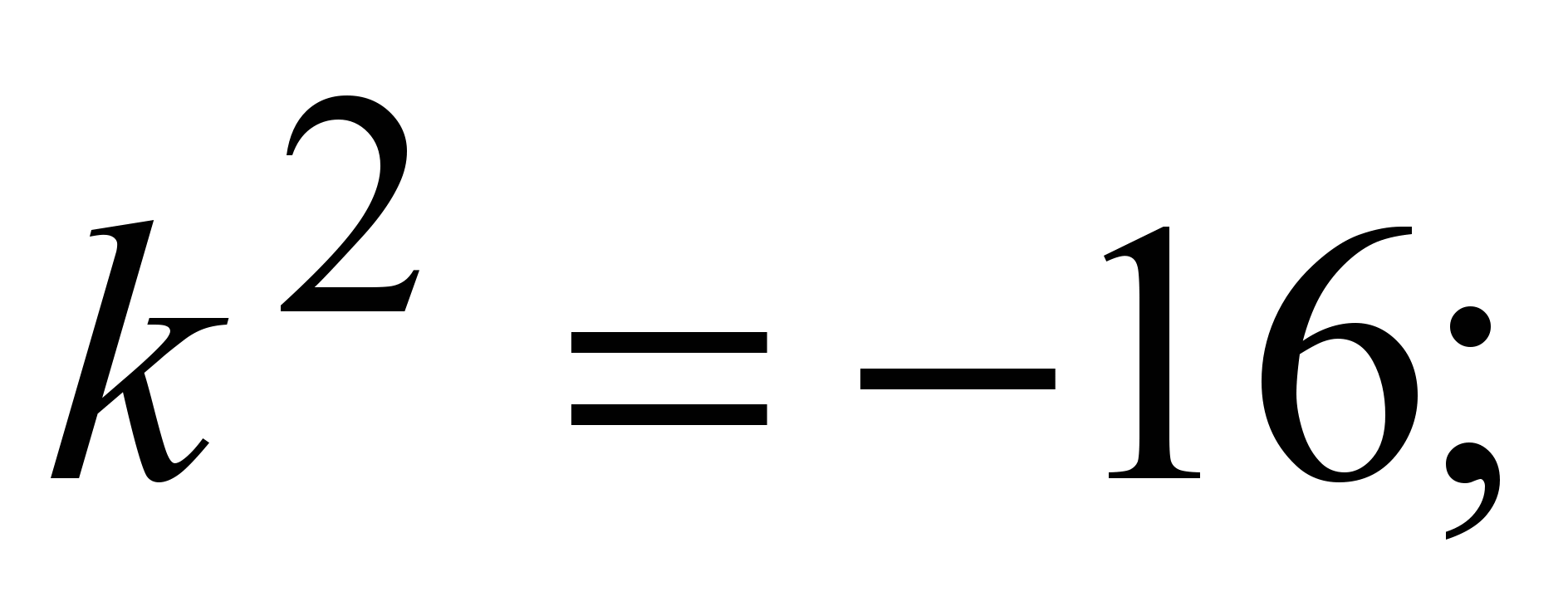 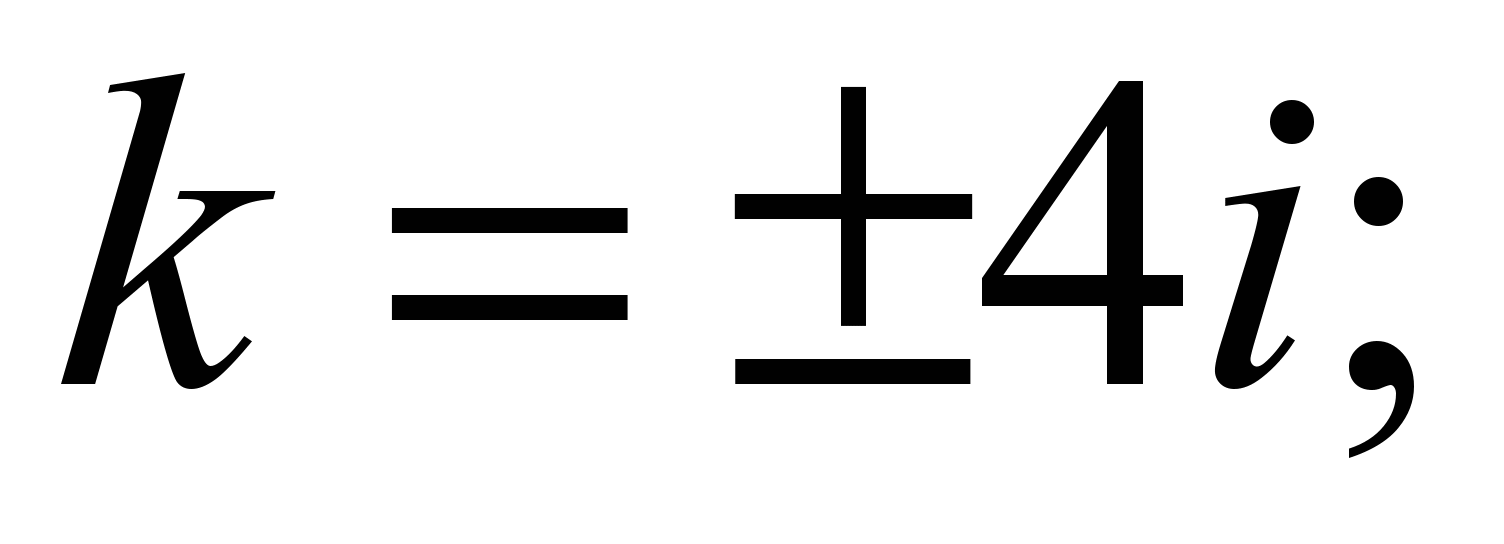
Общее решение: 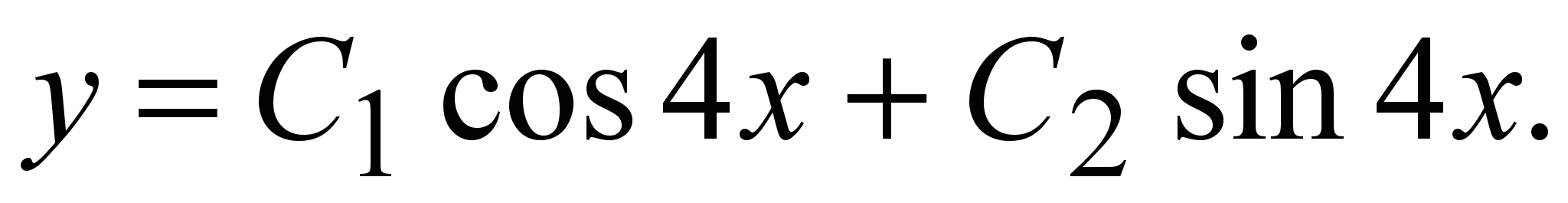
8)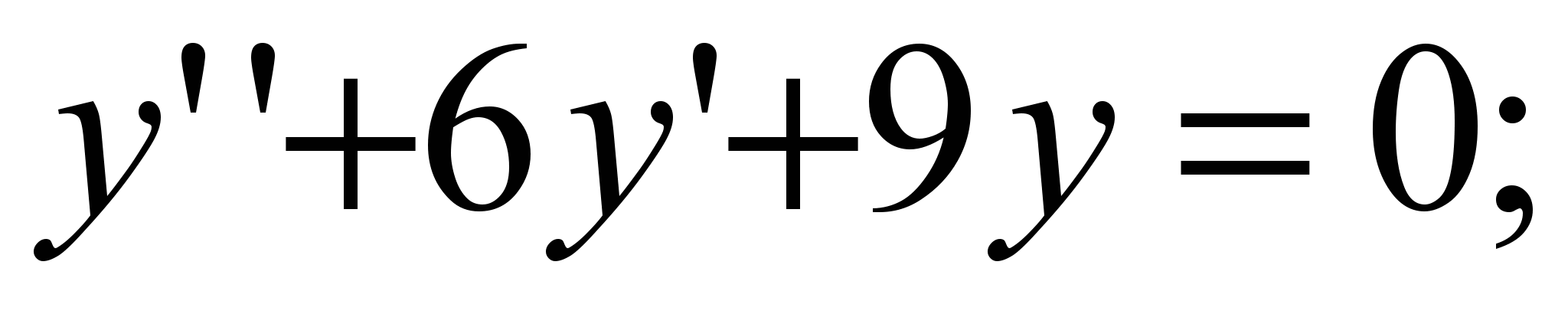 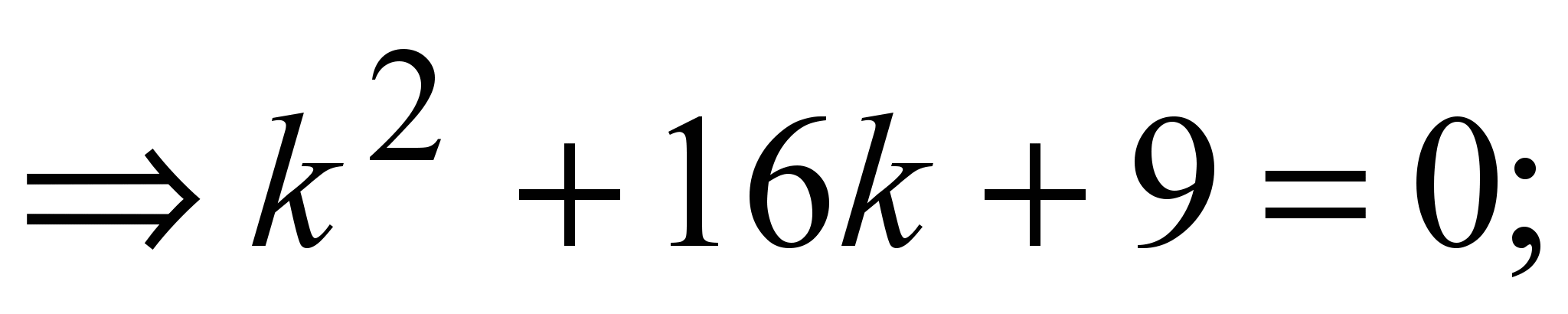 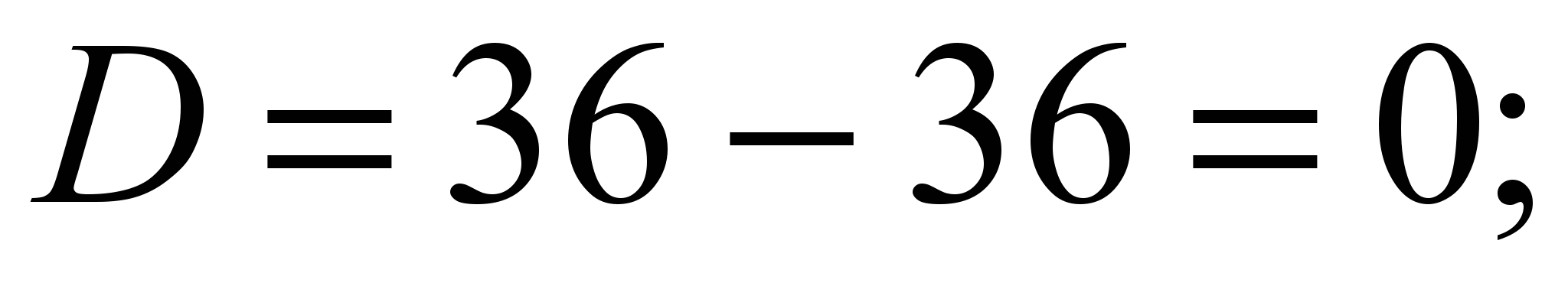 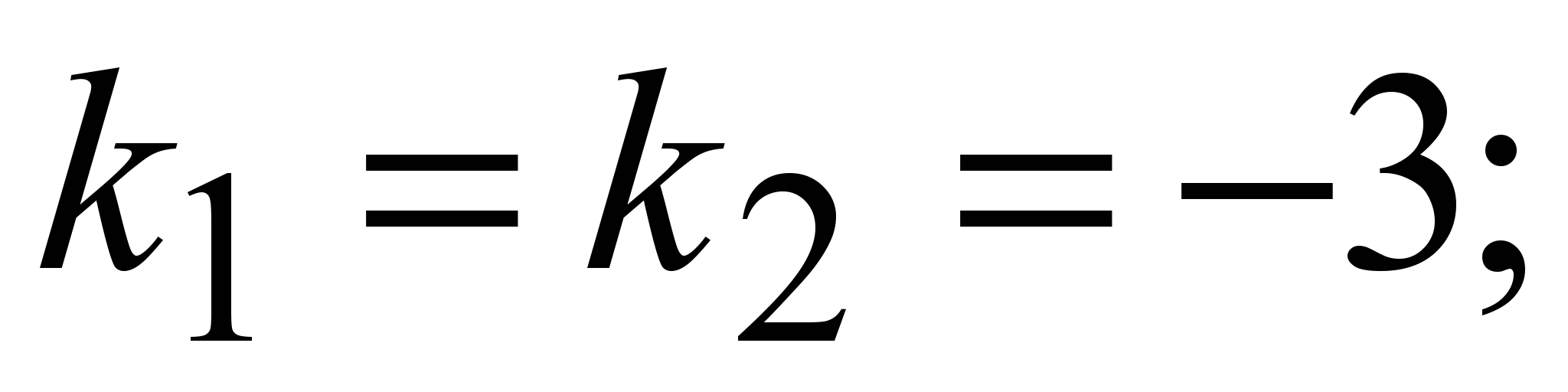
Общее решение: 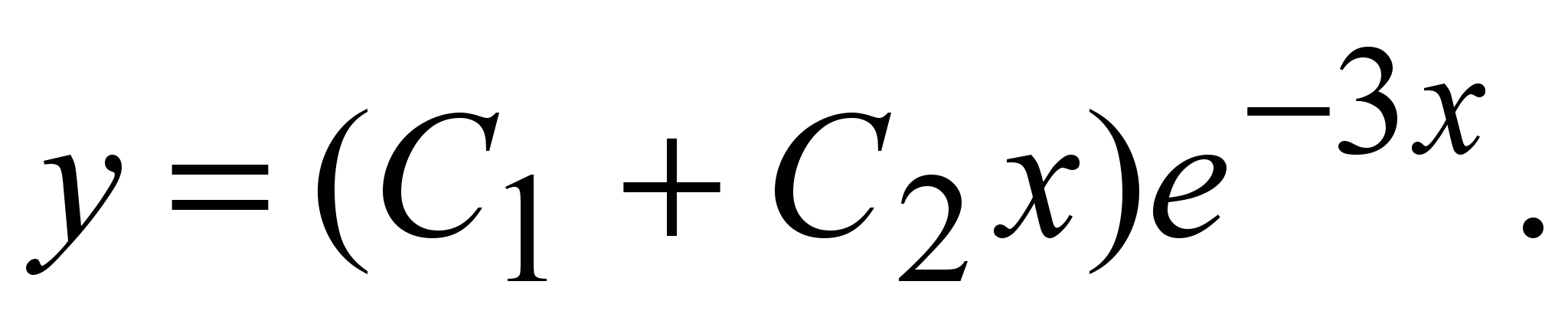
Самостоятельное работа
Найти общее решение следующих дифференциальных уравнений.
Задание 1. 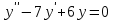
Решение:
Составим характеристическое уравнение:
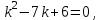
 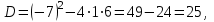
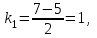 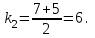
Общее решение данного дифференциального уравнения, согласно формуле(1), имеет вид:
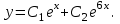
Ответ: 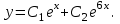
Задание 2. 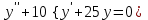
Решение:
Составим характеристическое уравнение:
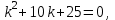
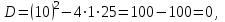
 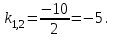
Общее решение данного дифференциального уравнения, согласно формуле(2), имеет вид:
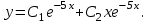
Ответ: 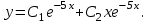
Задание 3. 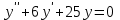 . .
Решение:
Составим характеристическое уравнение:
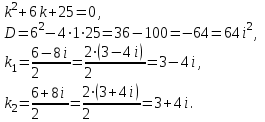
Общее решение данного дифференциального уравнения, согласно формуле(3), имеет вид:
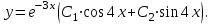
Ответ: 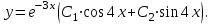
Задание 4 . 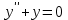
Составим характеристическое уравнение:
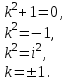
Это третий случай, где 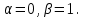
Общее решение данного дифференциального уравнения, согласно формуле(3), имеет вид:
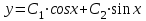
Ответ: 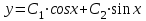
Задание 5.Найти частное решение дифференциального уравнения 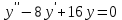 , если у(0)=1 и , если у(0)=1 и 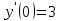 . .
Решение:
Составим характеристическое уравнение:
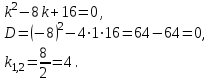
Общее решение данного дифференциального уравнения, согласно формуле(2), имеет вид:
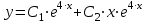
Так как заданы начальные условия, то:
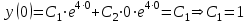
Чтобы найти значение 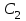 , дифференцируем общее решение. , дифференцируем общее решение.
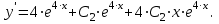
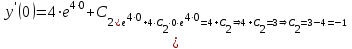
Таким образом, искомое частное решение имеет вид
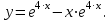
Ответ: 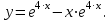
Решите дифференциальное уравнение: y′′+4y′+5y=0.
№2.Решите уравнение: y′′+25y=0.
№3. Найдите общее решение уравнения и выполните проверку: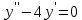
№4. Решите дифференциальное уравнение: 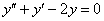
№5. Решите дифференциальное уравнение: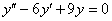
№6.Найдите общее решение уравнений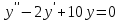 . .
№7. Решите однородное дифференциальное уравнения второго порядка: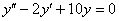
№8. Найти часное решение дифференциального уравнения, удовлетворяющее начальное условиям: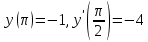 , ,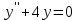 . .
Задания: 28.1, 28.2, 28.3, 28.4, 28.5, 28.6, 28.7
|
Внимательно слушает и высказывает свое мнение
Внимательно слушает и анализирует объясняемый материал
|
Устный комментарий учителя
Похвала учителя
Взаимооценивание
|
Презентация
|
Конец урока Рефлексия/3 мин.
Запись домашнего задания
|
Сегодня на уроке мне понравилось…
Сегодня на уроке я повторил…
Сегодня на уроке я закрепил…
Сегодня на уроке я поставил себе оценку …
Какие виды работ вызвали затруднения и требуют повторения…
В каких знаниях уверен…
Помог ли урок продвинуться в знаниях, умениях, навыках по предмету…
Кому, над, чем следовало бы ещё поработать…
Насколько результативным был урок сегодня…
|
производят рефлексию по пройденной теме по стратегии «незаконченные фразы»
записывают домашнее задание
|
Комментирует домашнее задание
|
| |
|
|
 Скачать 1.61 Mb.
Скачать 1.61 Mb.