ответы дифур. дифур. Решение уравнения Решить уравнение
 Скачать 194.48 Kb.
|
|
Найти общее решение уравнения   Решить уравнение   График решения дифференциального уравнения называется интегральной кривой дифференциального уравнения Решить краевую задачу   Решить уравнение   Суть метода Лагранжа заключается в вариации произвольной постоянной Решения линейной однородной системы дифференциальных уравнений асимптотически устойчивы, если действительные части всех корней характеристического уравнения отрицательны Решить краевую задачу   Указать тип уравнения:  уравнение с разделяющимися переменными Решить уравнение 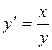  Решение дифференциального уравнения, в каждой точке которого нарушается единственность решения задачи Коши, называется особым решением дифференциального уравнения Решить уравнение   К какому типу дифференциальных уравнений относится уравнение: 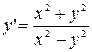 Однородному   Определить общий вид частного решения неоднородного уравнения   Найти общее решение уравнения Решить краевую задачу   Решить уравнение Решить дифференциальное уравнение   Характеристическое уравнение линейного однородного дифференциального уравнения n-го порядка с постоянными коэффициентами:  . имеет вид: Определите тип уравнения:  однородное; Указать тип уравнения:  уравнение с разделяющимися переменными Решить уравнение   К какому типу дифференциальных уравнений относится уравнение: 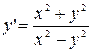 Однородному Найти общее решение уравнения   Указать тип уравнения  линейное уравнение График решения дифференциального уравнения называется интегральной кривой дифференциального уравнения 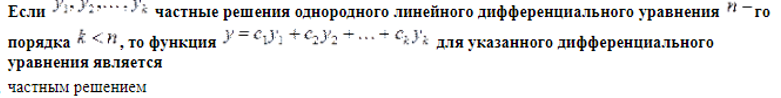  Жауап:   Жауап: 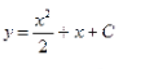 Если   образует фундаментальную систему решений однородного линейного дифференциального уравнения  го порядка, то его общее решение дается формулой Согласно методу вариации произвольных постоянных решение неоднородного линейного дифференциального уравнения n-го порядка 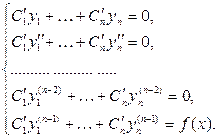 ищем в виде:  , где функции  определяются из следующей системы уравнений Дифференциальное уравнение вида  , где  и  - заданные функции, называетсядифференциальным уравнением с разделенными переменными Если в дифференциальном уравнении искомая функция есть функция одного независимого переменного, то дифференциальное уравнение называется Обыкновенным Функция  , зависящая от  произвольных постоянных  таких что:1)  удовлетворяет дифференциальному уравнению  при ,2) при заданных начальных условиях постоянные можно подобрать так, что функция  будет удовлетворять указанным начальным условиям; называетсяобщим решением дифференциального уравнения  -го порядкаРешить уравнение   Дифференциальное уравнение вида  где  - заданная функция, называется однородным дифференциальным уравнением, если  однородная функция нулевого измерения Любая система из  линейно независимых частных решений линейного однородного дифференциального уравнения  го порядка называетсяфундаментальной системой решений дифференциального уравнения Дифференциальное уравнение вида  где  - заданные функции, являетсядифференциальным уравнением с разделяющимися переменными К какому типу относится дифференциальное уравнение:  уравнение с разделенными переменными Дифференциальное уравнение вида  , где  и  - заданные функции, называется однородным дифференциальным уравнением, еслии  - однородные функции одного и того же измерения относительно  и  Соотношение, связывающее независимые переменные, искомую функцию и её производные, называется дифференциальным уравнением Найти общее решение уравнения: 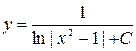  Решить уравнение   Порядком дифференциального уравнения называется порядок старшей производной, входящей в уравнение Решить уравнение   Корни характеристического уравнения  . Найти соответствующее дифференциальное уравнение Общее решение линейного неоднородного дифференциального уравнения имеет вид  где общее решение соответствующего однородного дифференциального уравнения,  частное решение исходного неоднородного дифференциального уравнения Какое из уравнений относится к уравнениям с разделяющимися переменными?  ;К уравнению первого порядка уравнение  можно привести с помощью замены Найти общее решение уравнения   Решить уравнение   Решить уравнение   Общее решение однородного линейного дифференциального уравнения первого порядка:  имеет вид: Решить систему дифференциальных уравнений 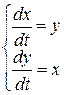   Дифференциальное уравнение Лагранжа интегрируется методом методом введения параметра К какому типу дифференциальных уравнений относится уравнение: 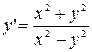Однородному Найти общее решение уравнения  Определить общий вид частного решения неоднородного уравнения   Исследовать особую точку системы 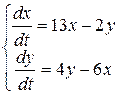 узел |