Ответы - РОСДИСТАНТ - Высшая математика 3. Итоговый тест попытка 1 Вопрос 1 Верно Баллов 1,0 из 1,0 Отметить вопрос Текст вопроса
 Скачать 3.93 Mb.
|
|
Итоговый тест попытка №1 Вопрос 1 Верно Баллов: 1,0 из 1,0  Отметить вопросТекст вопроса Даны линейные неоднородные дифференциальные уравнения второго порядка. Определите уравнение, которое можно решить методом Лагранжа неопределенных коэффициентов. Выберите один ответ:    Вопрос 2 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Разность комплексных чисел , равна: Выберите один ответ:  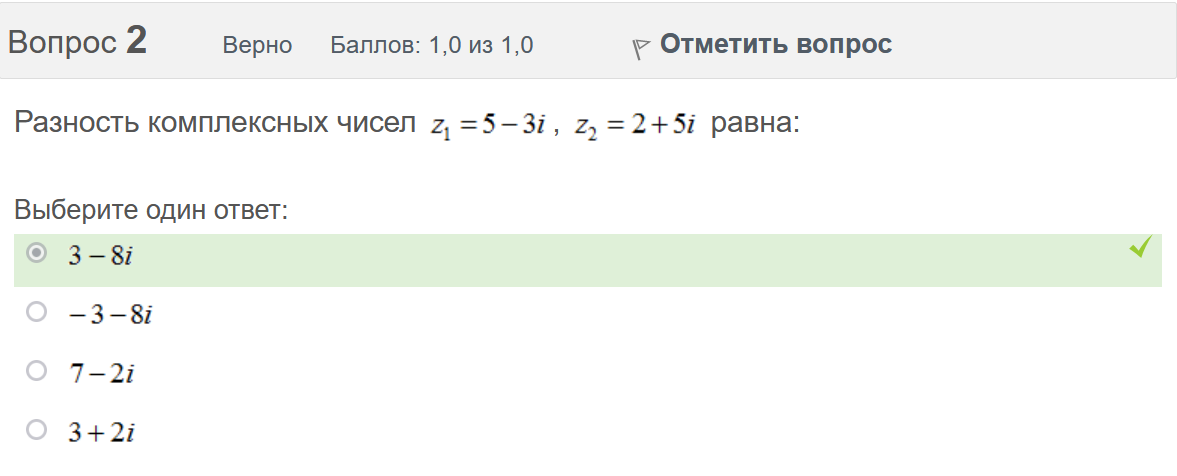Вопрос 3 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Вычислить sin(1 + i). Выберите один ответ:  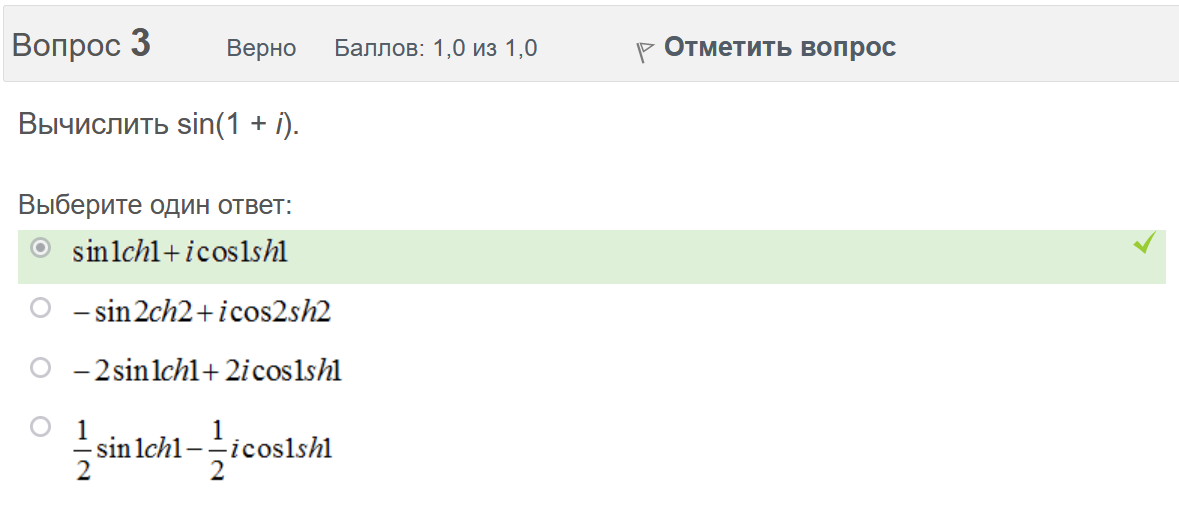Вопрос 4 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Частным решением дифференциального уравнения 1-го порядка является функция Выберите один ответ:  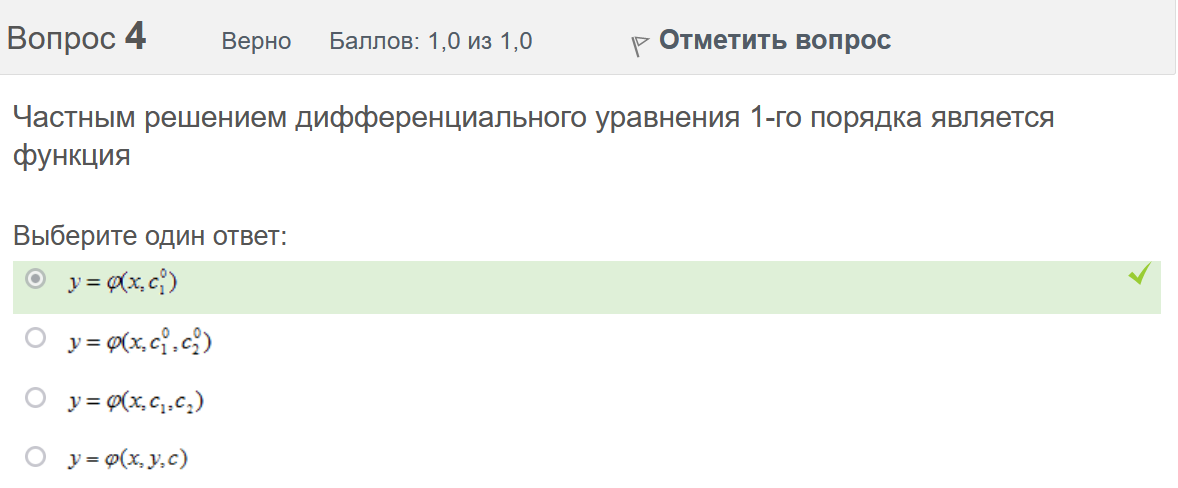Вопрос 5 Частично правильный Баллов: 0,7 из 1,0 Отметить вопросТекст вопроса Даны линейные неоднородные дифференциальные уравнения второго порядка. Определите уравнения, которые НЕ являются уравнениями с правой частью специального вида. Выберите один или несколько ответов:    Вопрос 6 Частично правильный Баллов: 0,7 из 1,0 Отметить вопросТекст вопроса Даны линейные неоднородные дифференциальные уравнения второго порядка. Определите уравнения, которые НЕ являются уравнениями с правой частью специального вида. Выберите один или несколько ответов:  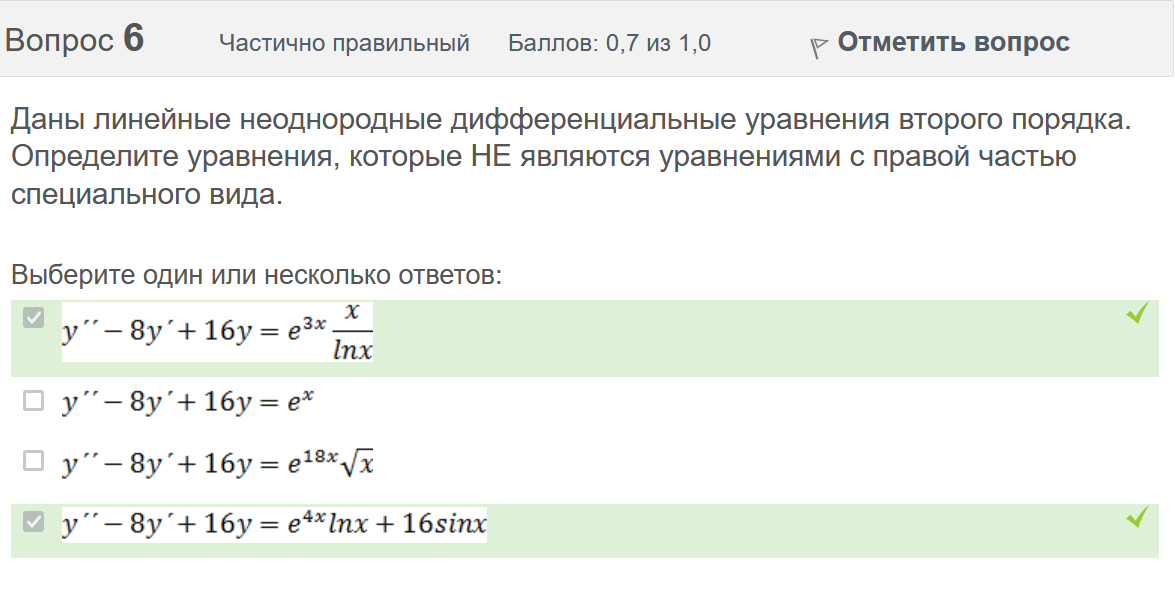Вопрос 7 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Какую из перечисленных функций вычисляют при помощи формулы ? Выберите один ответ:  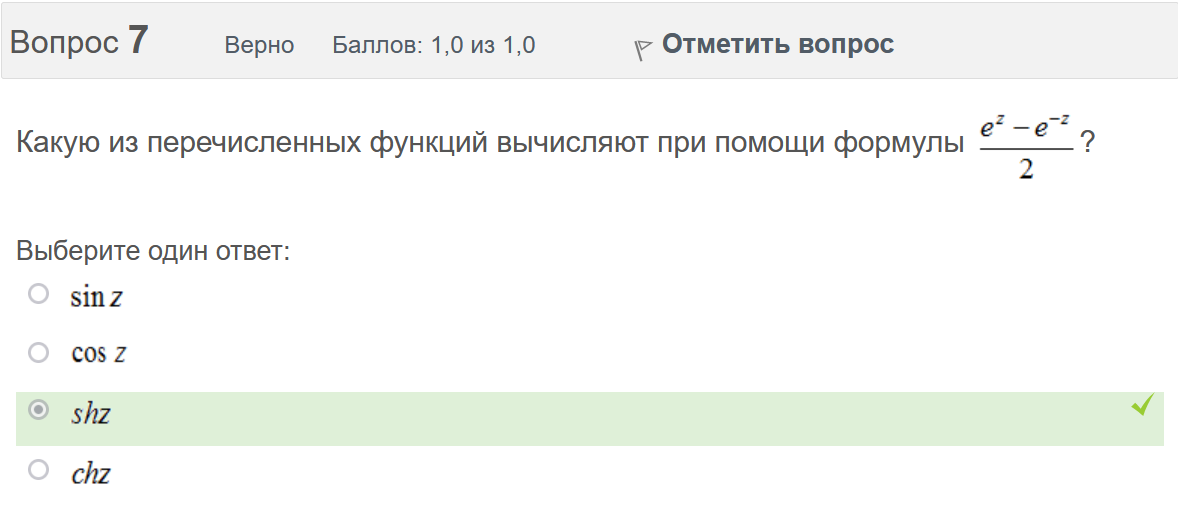Вопрос 8 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Укажите функции, которые линейно зависимы для функции . Выберите один или несколько ответов: 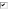 Вопрос 9 Неверно Баллов: 0,0 из 1,0 Отметить вопросТекст вопроса Замена приводит дифференциальное уравнение к уравнению с разделенными переменными, которое имеет вид: Выберите один ответ:  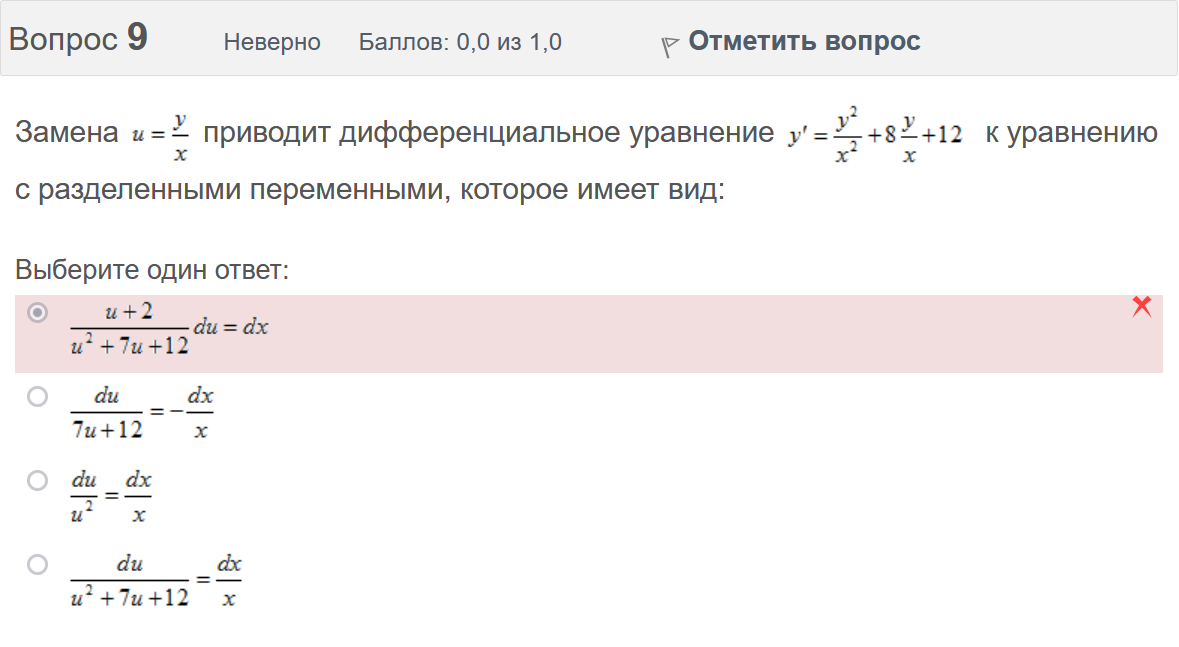Вопрос 10 Неверно Баллов: 0,0 из 1,0 Отметить вопросТекст вопроса Даны линейные неоднородные дифференциальные уравнения второго порядка. Определите уравнения, которые являются уравнениями с правой частью специального вида. Выберите один или несколько ответов: 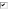 Вопрос 11 Неверно Баллов: 0,0 из 1,0 Отметить вопросТекст вопроса После применения подстановки дифференциальное уравнение приводится к уравнению вида: Выберите один ответ:  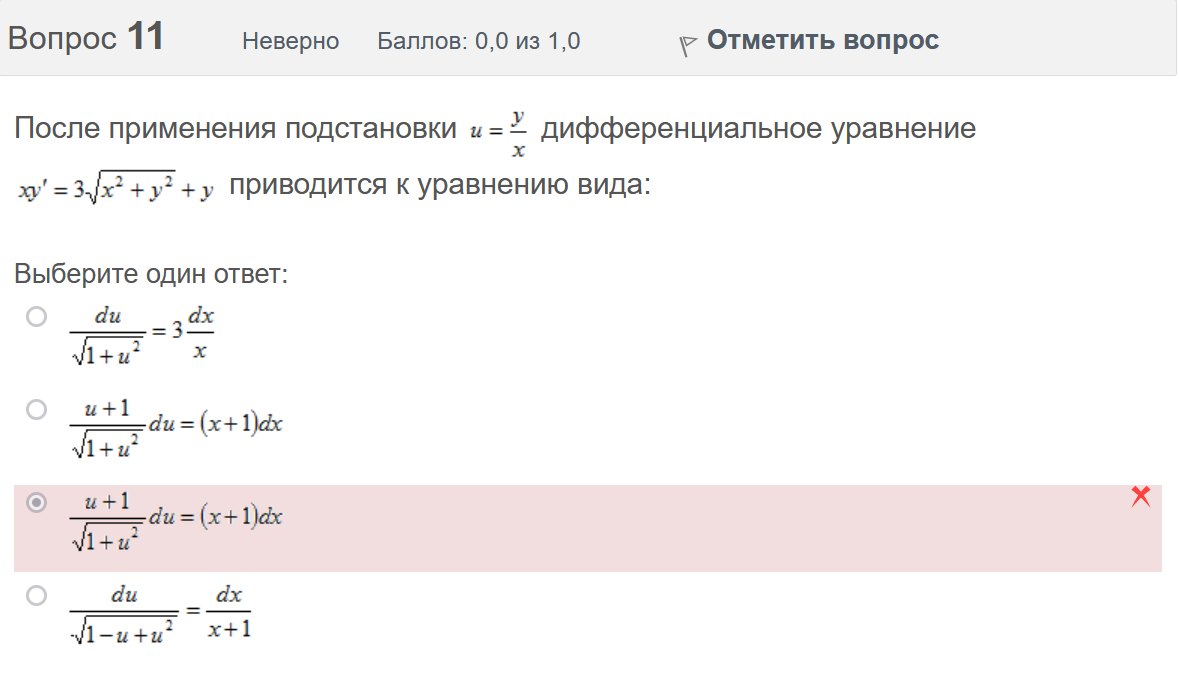Вопрос 12 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Если , то равно Ответ:  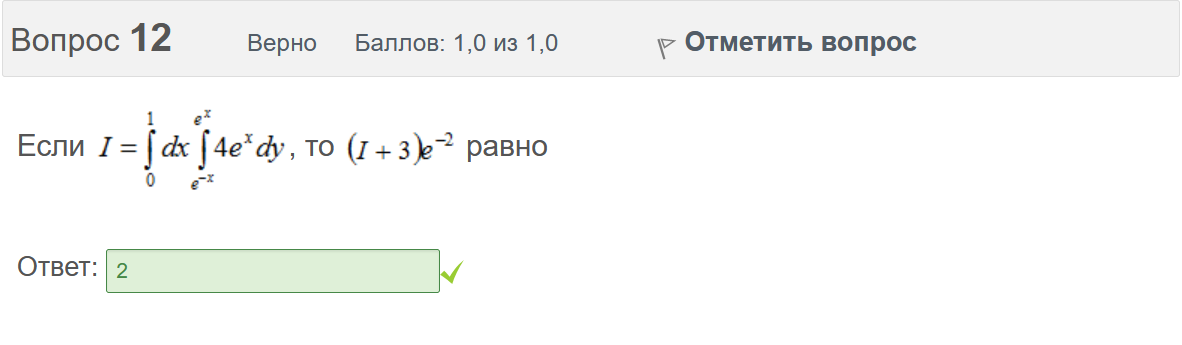 Вопрос 13 Неверно Баллов: 0,0 из 1,0 Отметить вопросТекст вопроса Дано линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами . Определите значение параметра а, при котором корни соответствующего характеристического уравнения равны. Ответ:  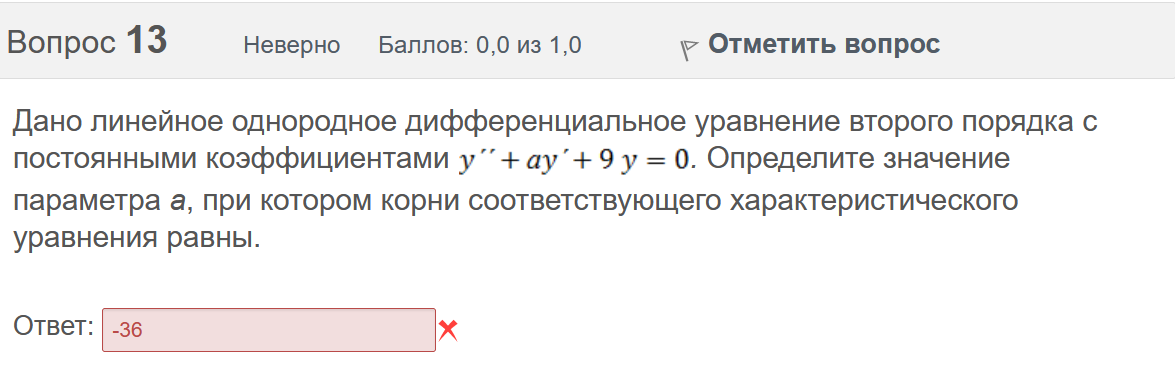 Вопрос 14 Неверно Баллов: 0,0 из 1,0 Отметить вопросТекст вопроса Чтобы уравнение было в полных дифференциалах, параметр А должен иметь значение ... Ответ:  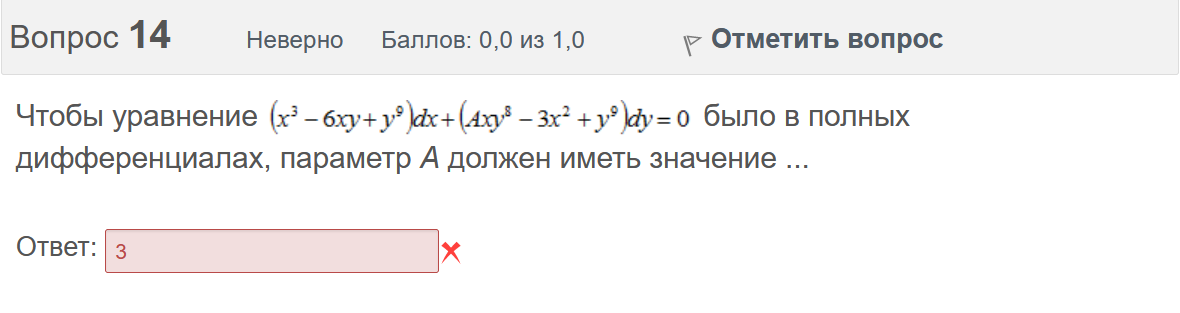 Вопрос 15 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Какие утверждения выражают свойства двойного интеграла? Выберите один или несколько ответов: Если подынтегральная функция непрерывна на области интегрирования и её границе, то внутри этой области найдётся точка, в которой значение подынтегральной функции равно двойному интегралу, делённому на площадь области интегрирования Если разделить область интегрирования D на две части D1 и D2, то двойной интеграл по области D равен произведению двойных интегралов по областям D1 и D2 Значение двойного интеграла больше произведения площади области интегрирования на наименьшее значение подынтегральной функции на этой области Двойной интеграл от большей функции будет больше двойного интеграла от меньшей функции  Вопрос 16 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Общее решение дифференциального уравнения имеет вид: Выберите один ответ:  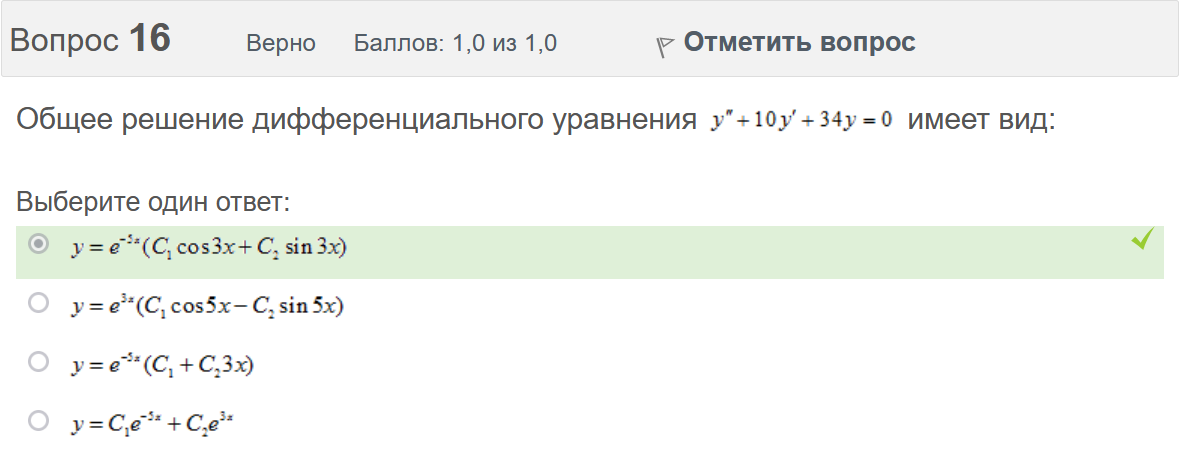Вопрос 17 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса В результате решения дифференциального уравнения второго порядка с постоянными коэффициентами получился ответ . Выберите один ответ: Это общее решение дифференциального уравнения. Это частное решение соответствующего однородного уравнения. Это частное решение дифференциального уравнения. Это общее решение соответствующего однородного уравнения.  Вопрос 18 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Даны линейные неоднородные дифференциальные уравнения второго порядка. Определите уравнения, которые НЕ являются уравнениями с правой частью специального вида. Выберите один или несколько ответов: 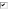 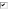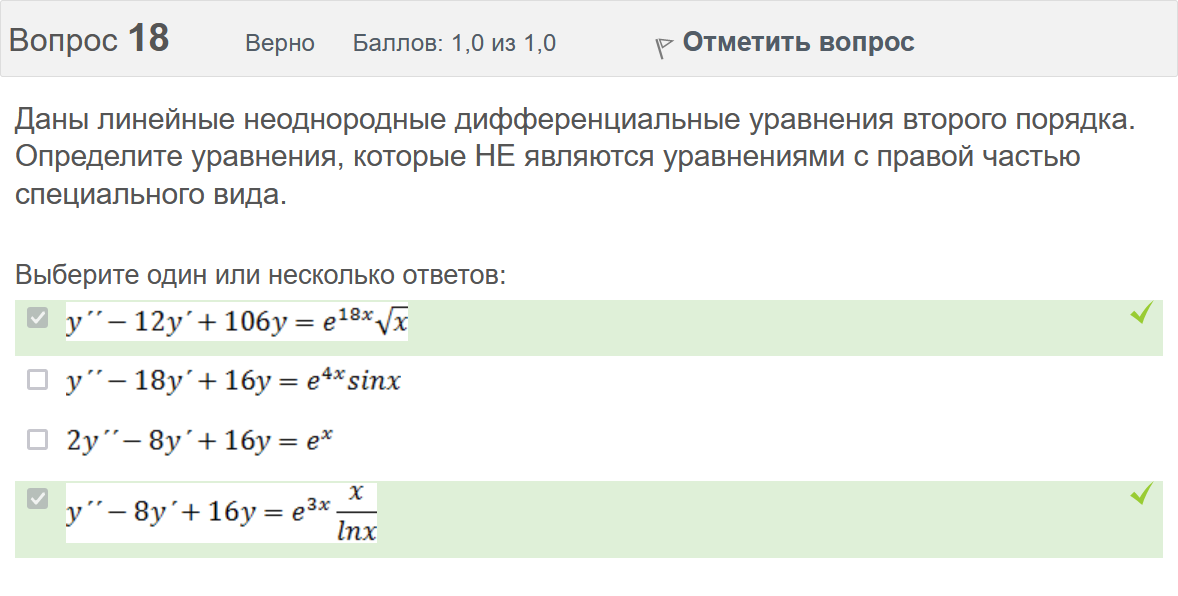Вопрос 19 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Для дифференциального уравнения указать возможный вид его частного решения. Выберите один ответ:  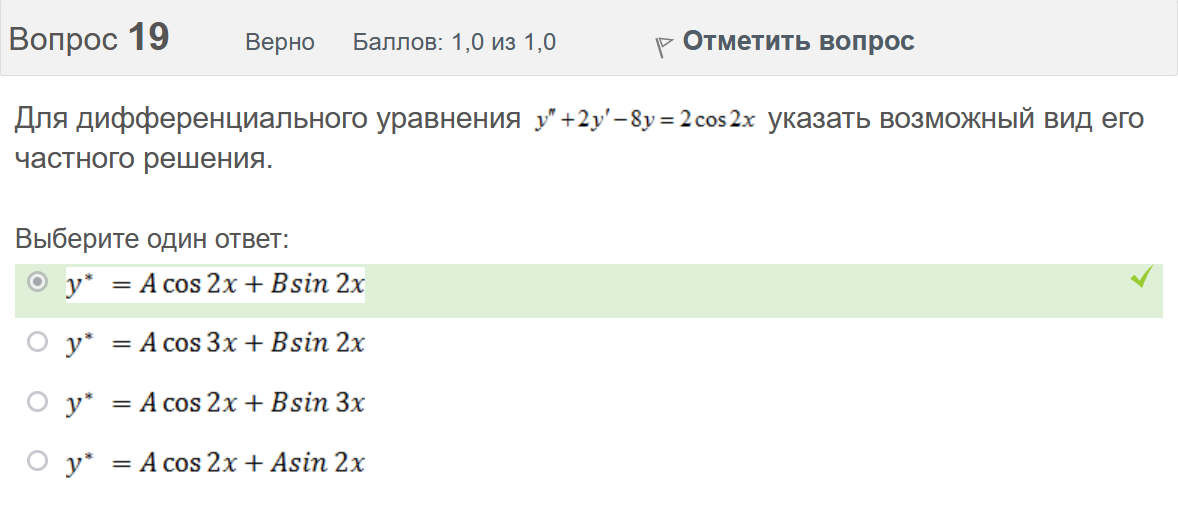Вопрос 20 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса В какой последовательности надо выполнить перечисленные ниже действия, чтобы вычислить двойной интеграл по правильной области интегрирования D?
Начало формы
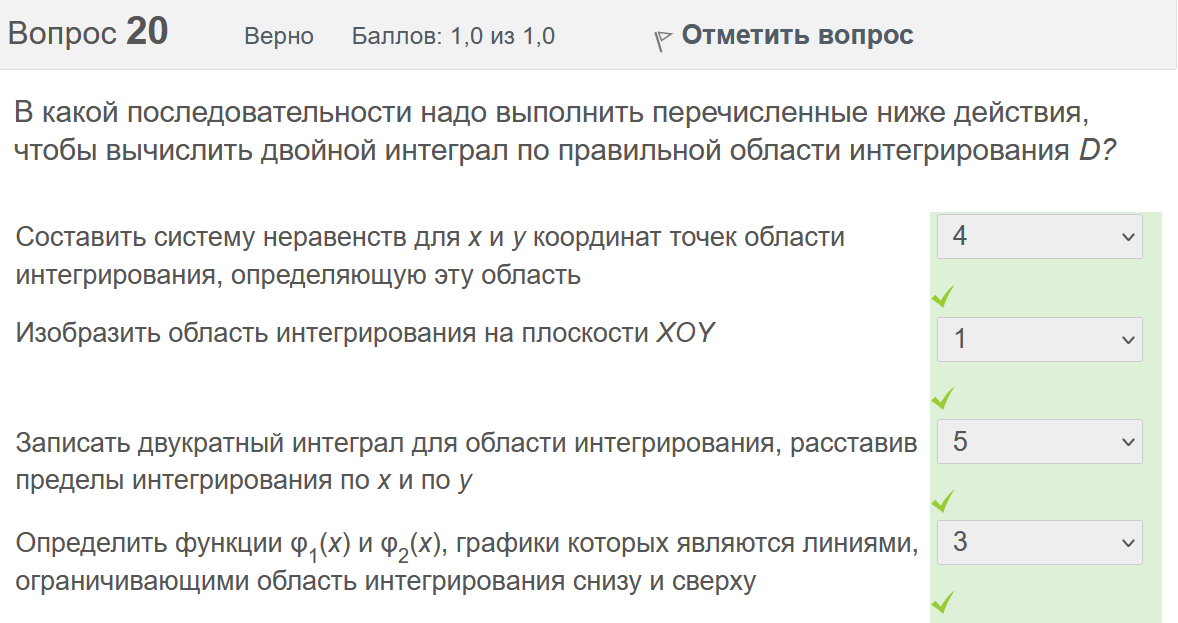  Вопрос 21 Неверно Баллов: 0,0 из 1,0 Отметить вопросТекст вопроса Среди предложенных функций выберите линейно независимую функцию для функции. Выберите один ответ:  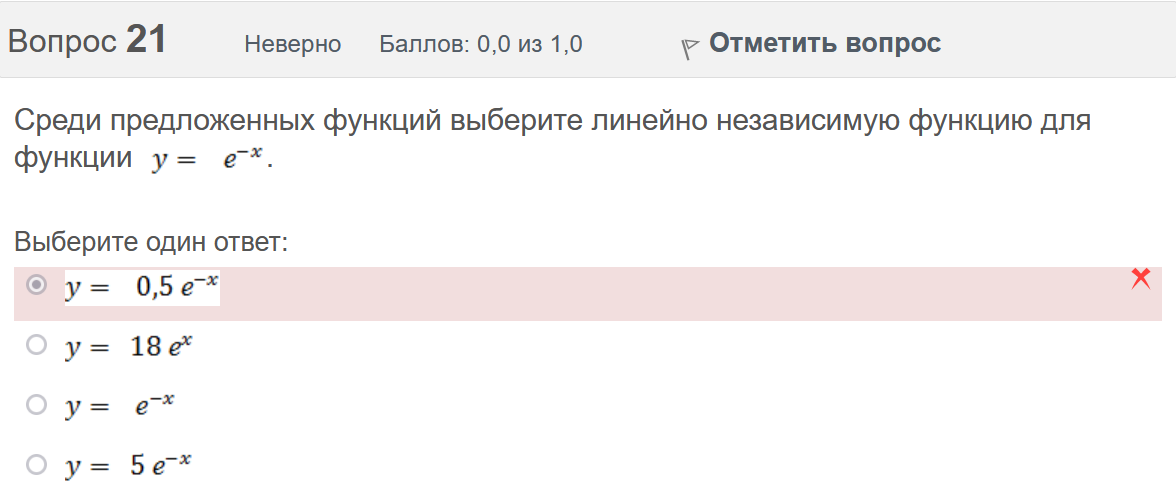Вопрос 22 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Дифференциальное уравнение первого порядка решается с помощью Выберите один ответ: дифференцирования двукратного дифференцирования двукратного интегрирования однократного интегрирования Вопрос 23 Частично правильный Баллов: 0,5 из 1,0 Отметить вопросТекст вопроса Укажите дифференциальное уравнение второго порядка, характеристическое уравнение которого имеет комплексные корни. Выберите один или несколько ответов:  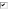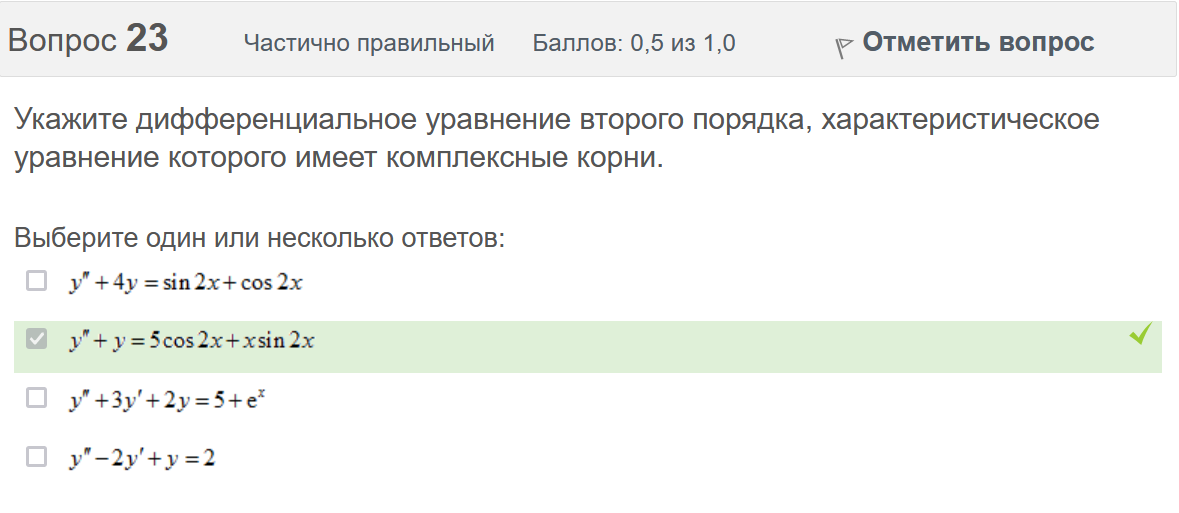Вопрос 24 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Разность комплексных чисел , равна: Выберите один ответ:  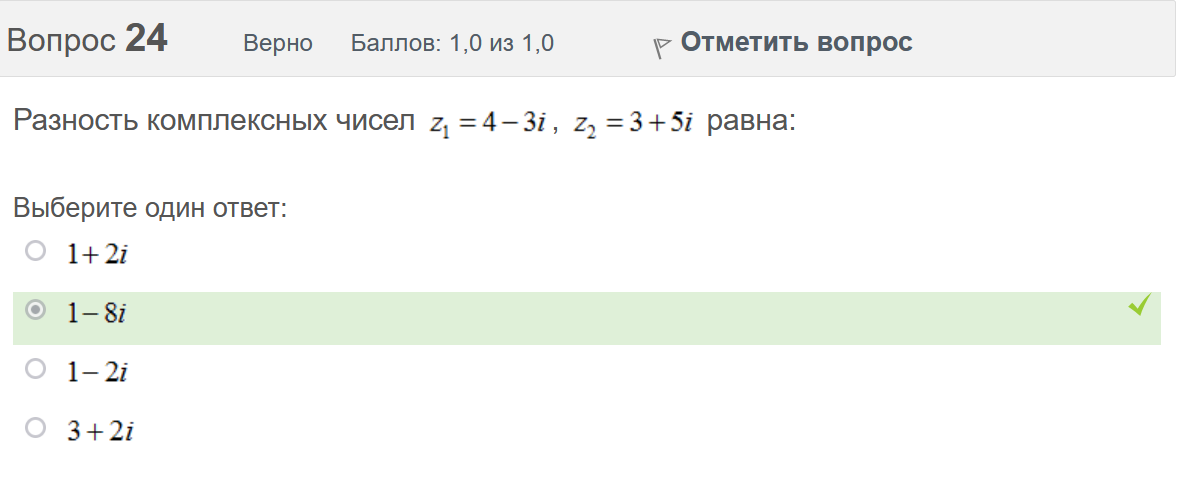Вопрос 25 Неверно Баллов: 0,0 из 1,0 Отметить вопросТекст вопроса Тело ограничено сверху поверхностью . Боковая поверхность тела параллельна оси OZ. Основание тела – область D на плоскости XOY, которая ограничена линиями ; ; ; . Тогда объём тела равен Ответ:  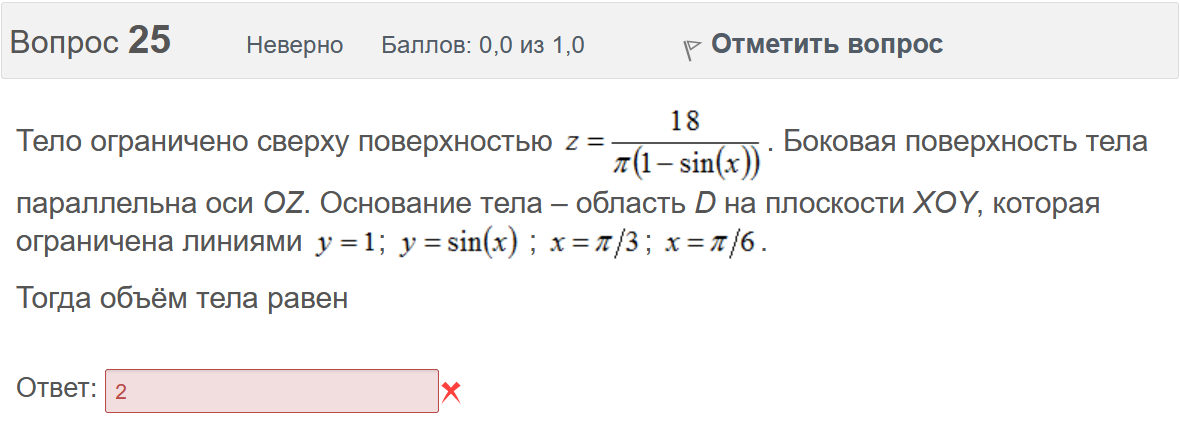Вопрос 26 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Уравнение является Выберите один ответ: дифференциальным уравнением с разделяющимися переменными уравнением Бернулли однородным относительно и дифференциальным уравнением 1-го порядка линейным дифференциальным уравнением первого порядка 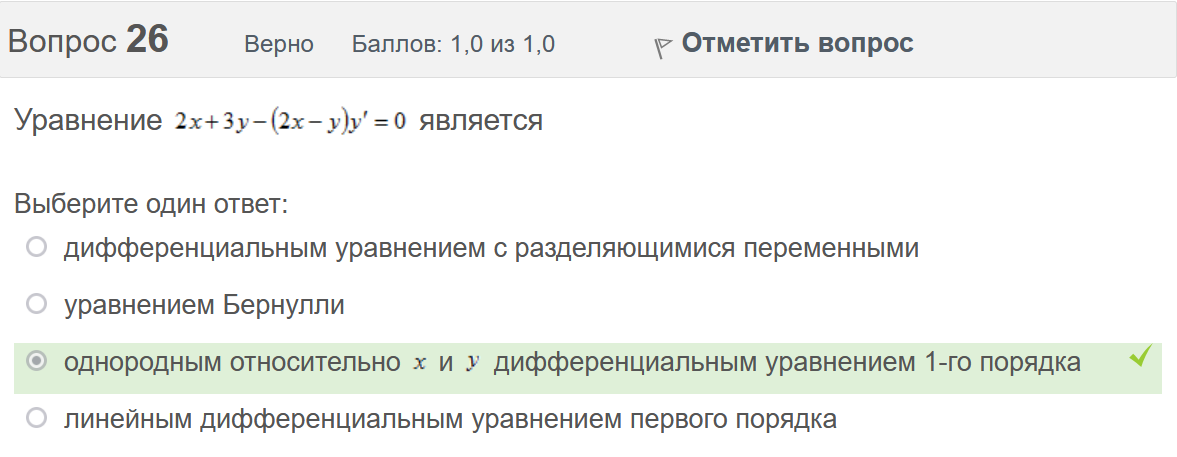 Вопрос 27 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Комплексное число задано в тригонометрической форме . Тогда алгебраическая форма записи имеет вид: Выберите один ответ:  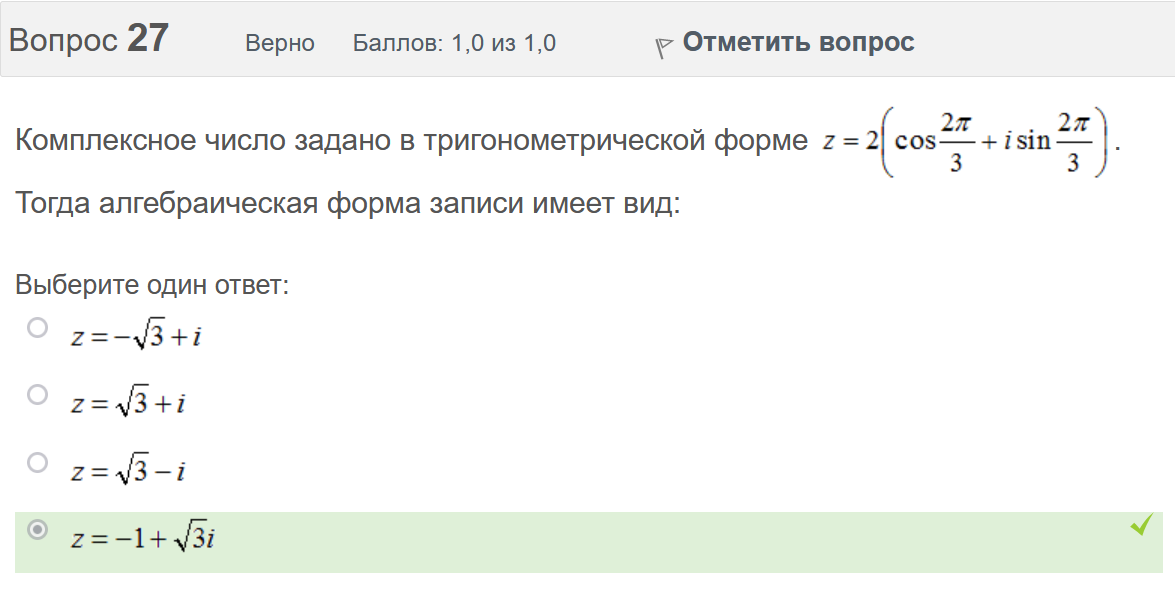Вопрос 28 Неверно Баллов: 0,0 из 1,0 Отметить вопросТекст вопроса Даны линейные неоднородные дифференциальные уравнения второго порядка. Определите уравнение, которое можно решить методом Лагранжа неопределенных коэффициентов. Выберите один ответ:  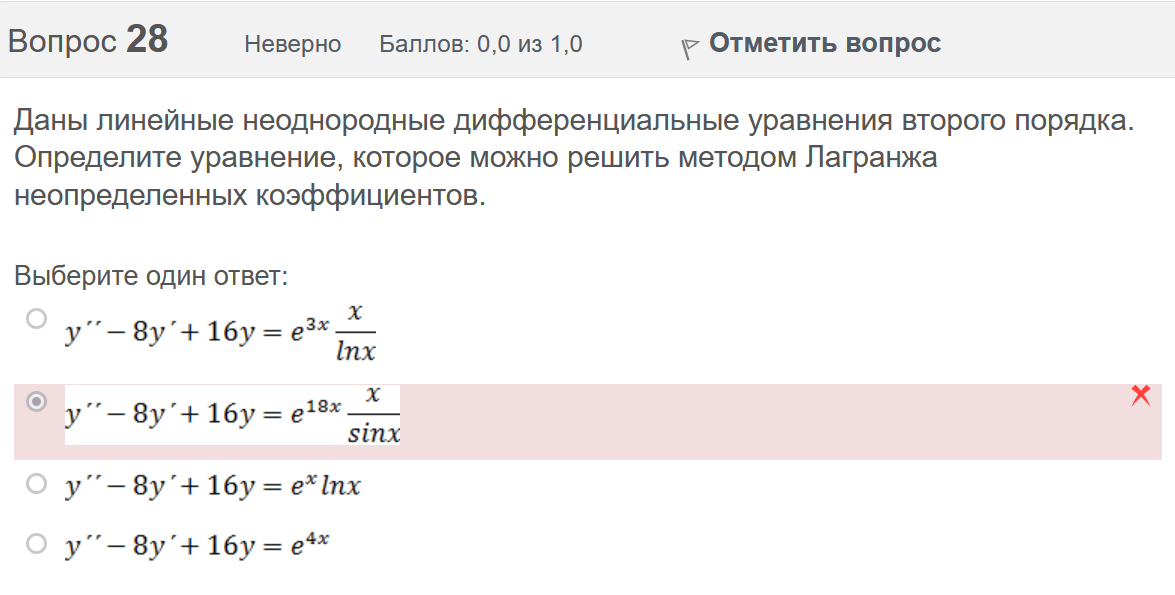Вопрос 29 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Область D на плоскости XOY ограничена линиями ; ; . Плотность вещества на D – . Если M – масса области D, то равно Ответ:  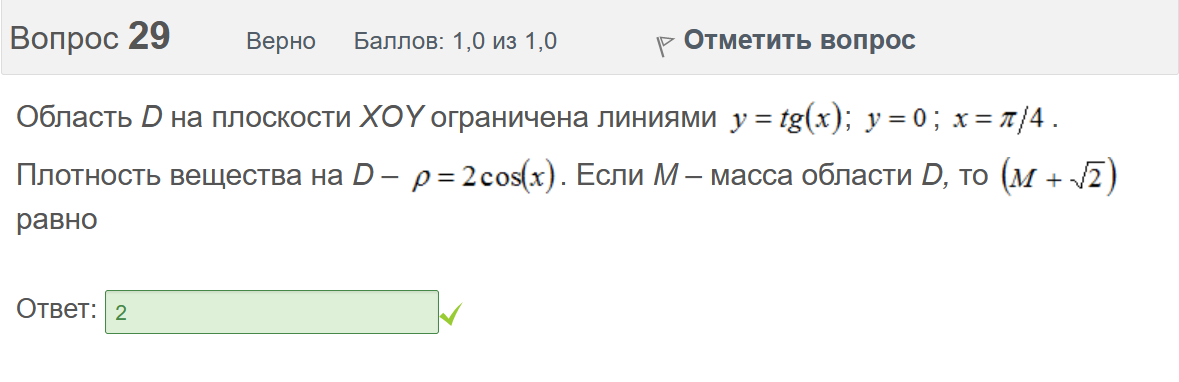Вопрос 30 Неверно Баллов: 0,0 из 1,0 Отметить вопросТекст вопроса Однородное дифференциальное уравнение можно записать в виде: Выберите один ответ:  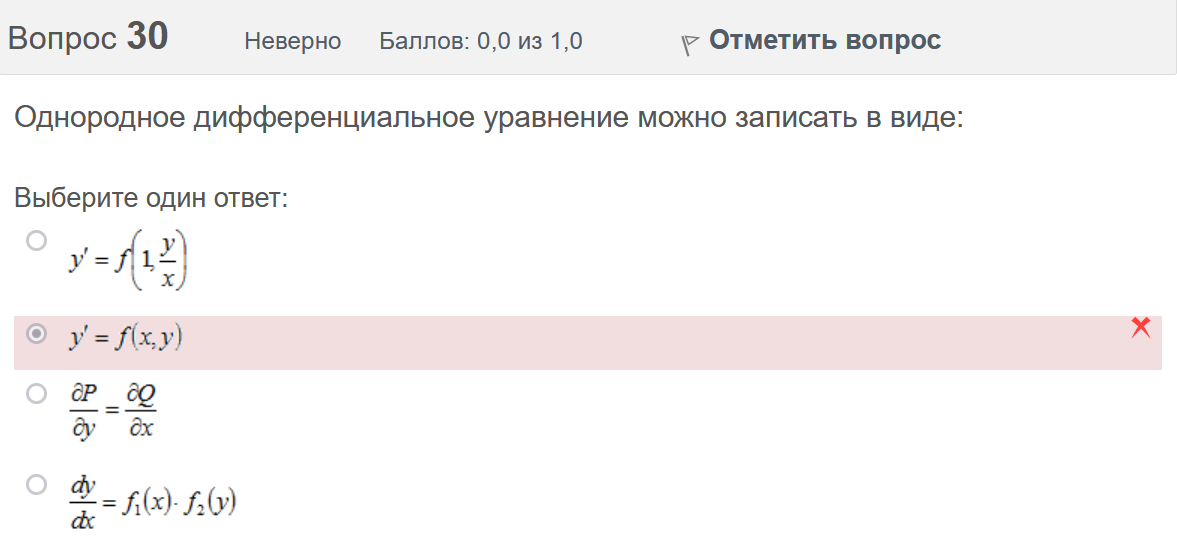Итоговый тест попытка №2 Вопрос 1 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Двукратный интеграл равен Ответ:  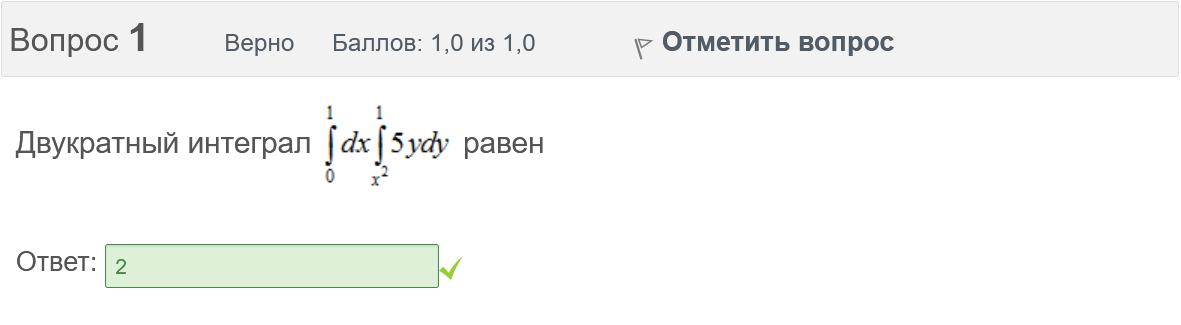Вопрос 2 Частично правильный Баллов: 0,7 из 1,0 Отметить вопросТекст вопроса Последовательность действий при решении линейного дифференциального уравнения следующая:
Начало формы
 Вопрос 3 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Даны линейные неоднородные дифференциальные уравнения второго порядка. Определите уравнение, которое можно решить методом Лагранжа неопределенных коэффициентов. Выберите один ответ:  Вопрос 4 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Данное дифференциальное уравнение имеет общее решение вида: Выберите один ответ:  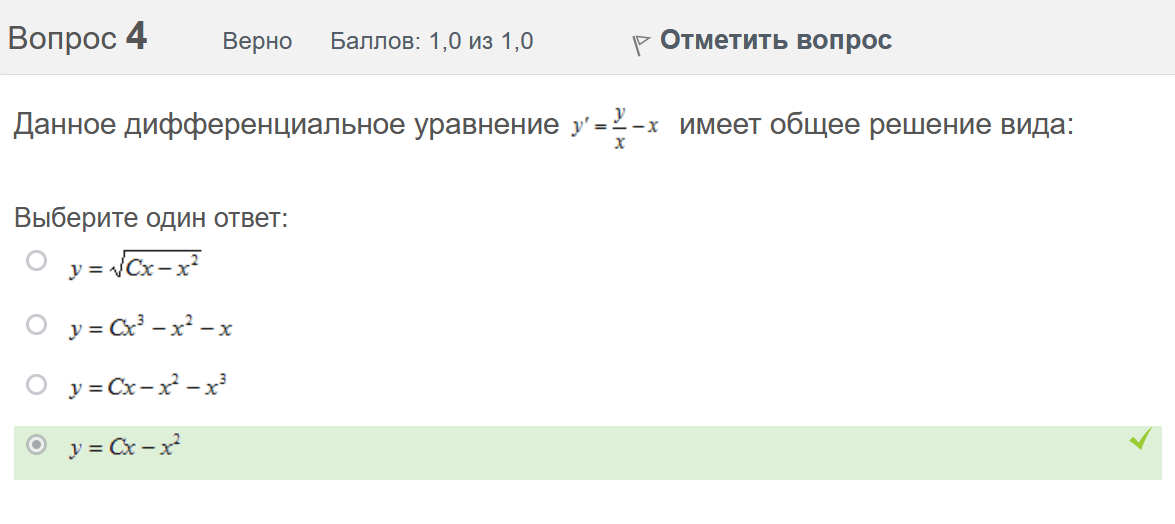Вопрос 5 Неверно Баллов: 0,0 из 1,0 Отметить вопросТекст вопроса Найти определитель Вронского для системы функций: и . Выберите один ответ:  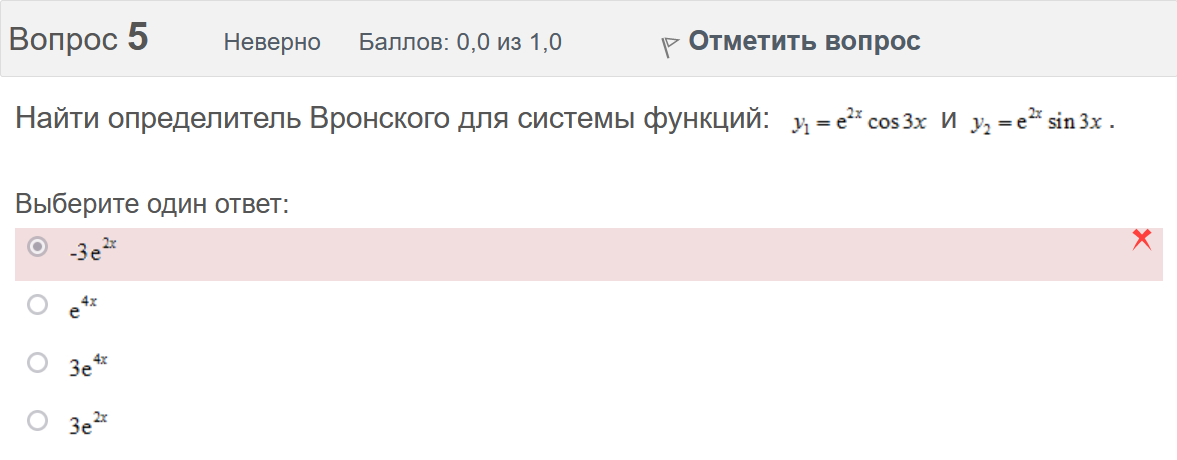Вопрос 6 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Укажите уравнение Бернулли. Выберите один ответ:  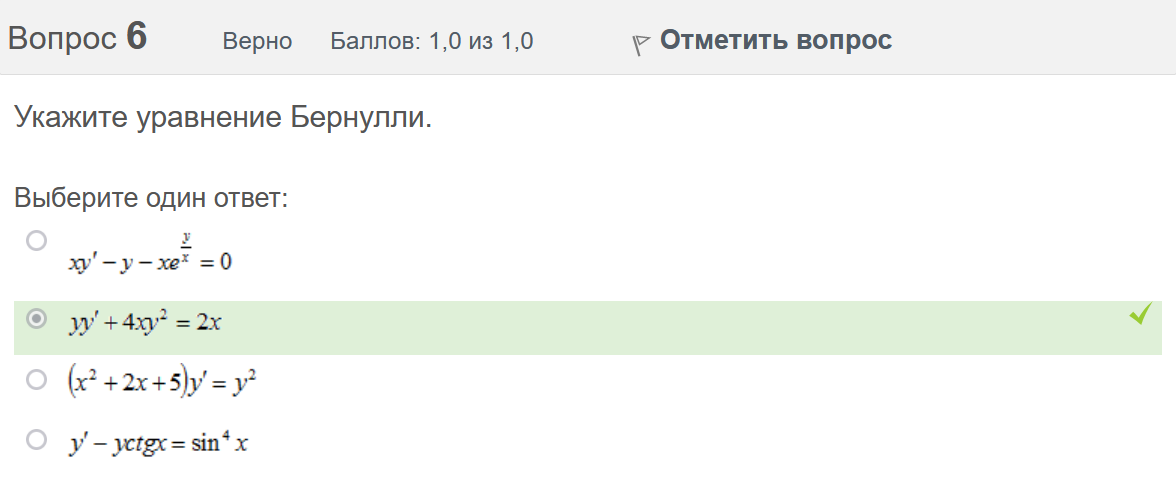Вопрос 7 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса В каком виде можно записать дифференциальное уравнение с разделяющимися переменными? Выберите один ответ:  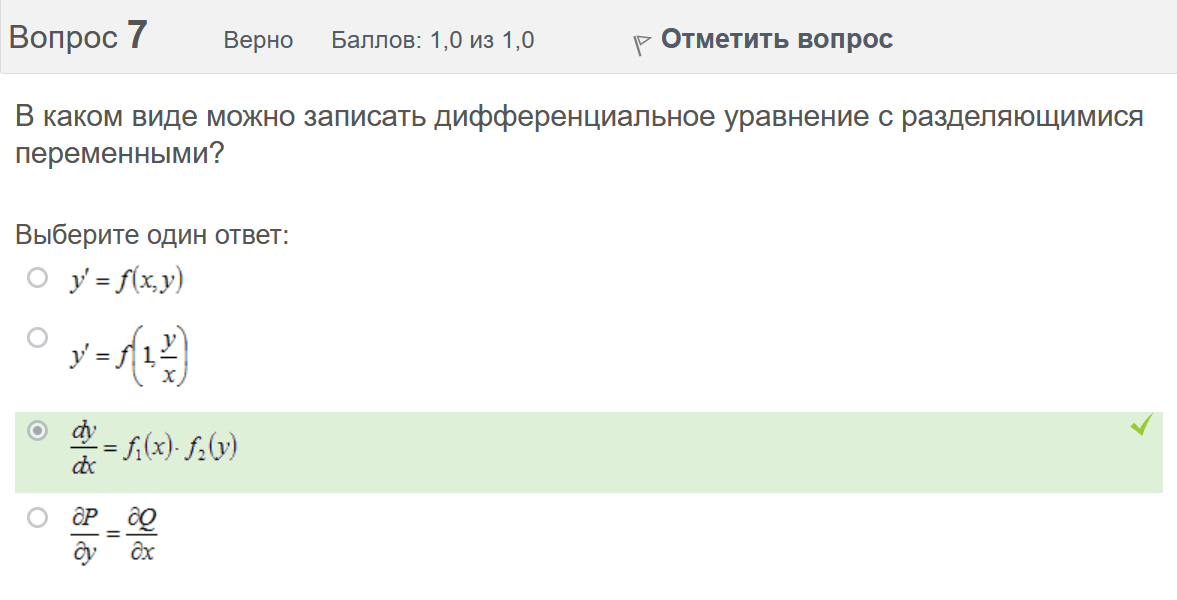Вопрос 8 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Записать в показательной форме число 2. Выберите один ответ:  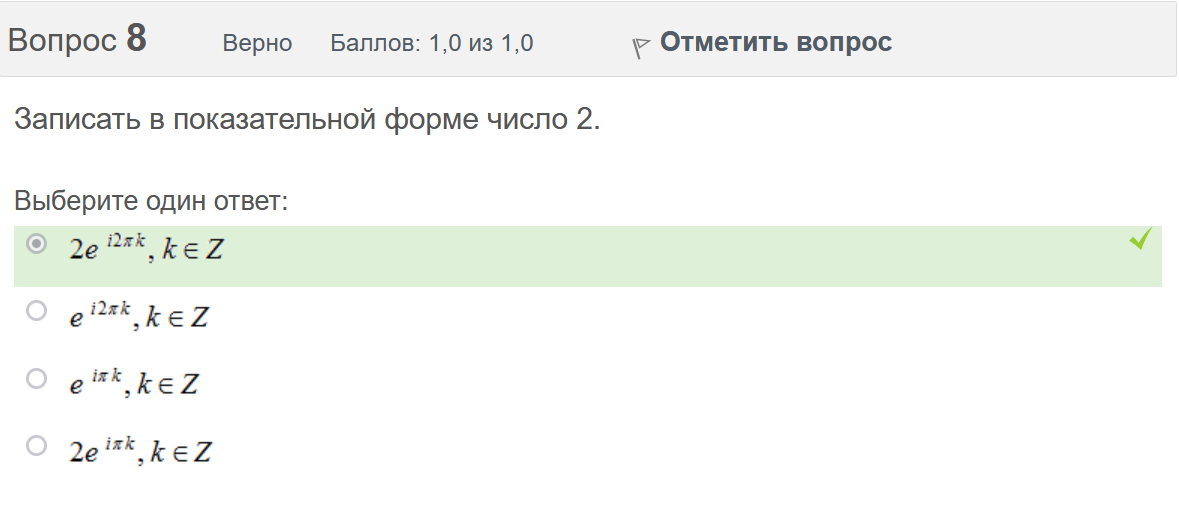Вопрос 9 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Область D на плоскости XOY есть ΔАВС с вершинами A(0, 0), B(3, 6), C(3, 15). Плотность вещества на D – . Тогда x-координата центра масс области D равна Ответ:  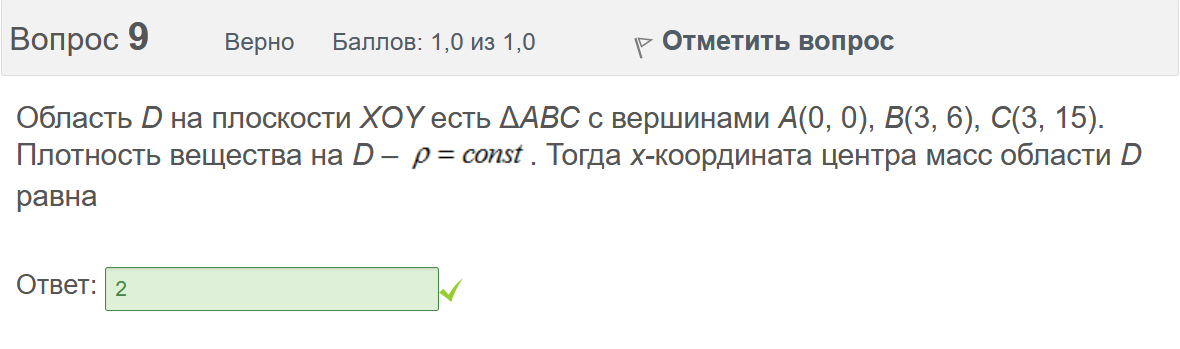Вопрос 10 Неверно Баллов: 0,0 из 1,0 Отметить вопросТекст вопроса Дана функция . Тогда равно: Ответ:  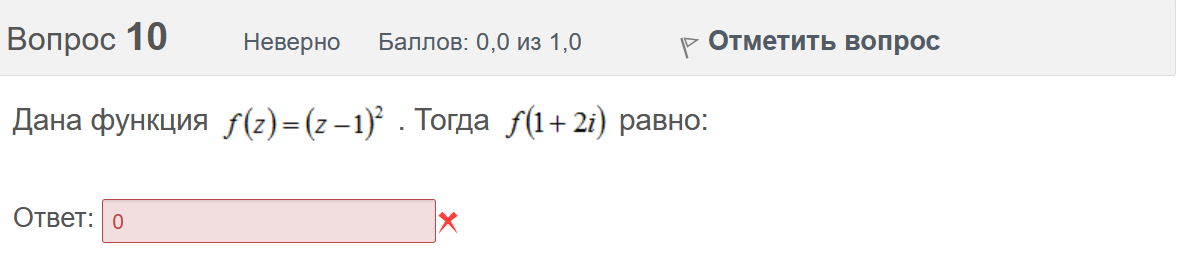 Вопрос 11 Неверно Баллов: 0,0 из 1,0 Отметить вопросТекст вопроса Для дифференциального уравнения указать способ решения, приводящего к понижению порядка. Выберите один ответ: сделать замену последовательное интегрирование сделать замену сделать замену 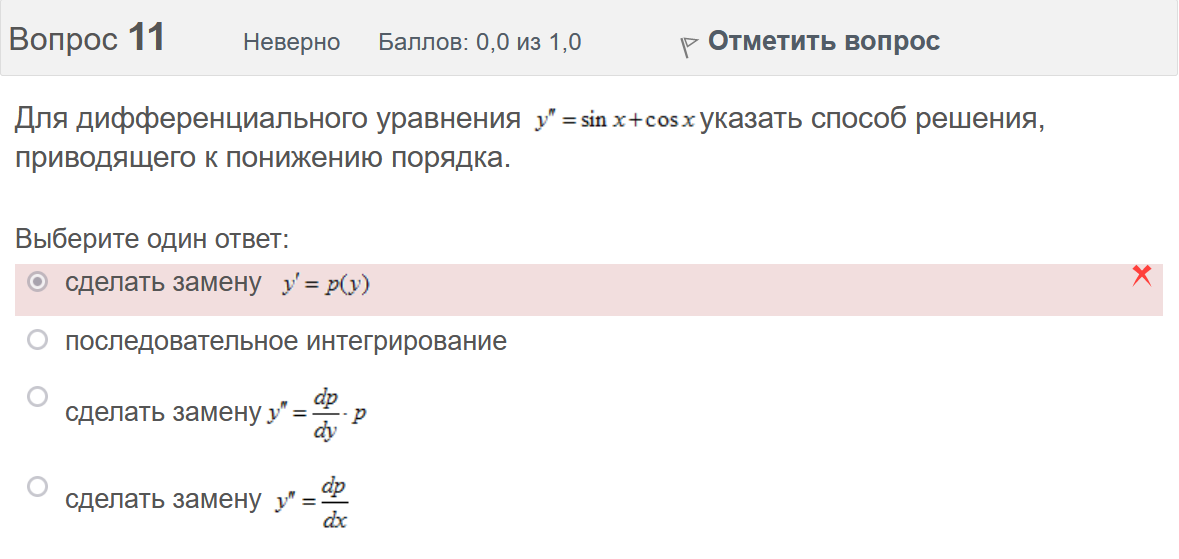 Вопрос 12 Неверно Баллов: 0,0 из 1,0 Отметить вопросТекст вопроса Тело ограничено сверху поверхностью. Боковая поверхность тела параллельна оси OZ. Основание тела – область D на плоскости XOY, которая ограничена линиями ; ; ; . Тогда объём тела равен Ответ:  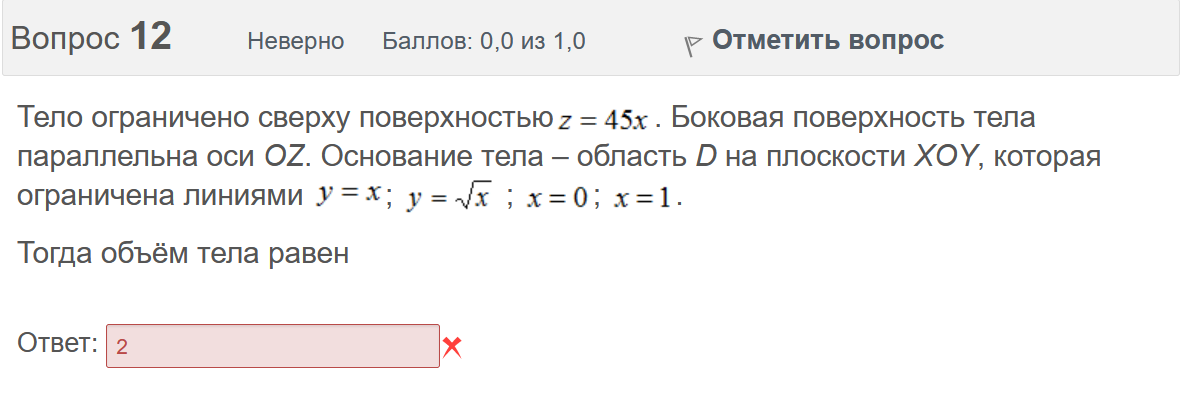Вопрос 13 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Область D на плоскости XOY ограничена линиями ; ; ; . Тогда равен Ответ:  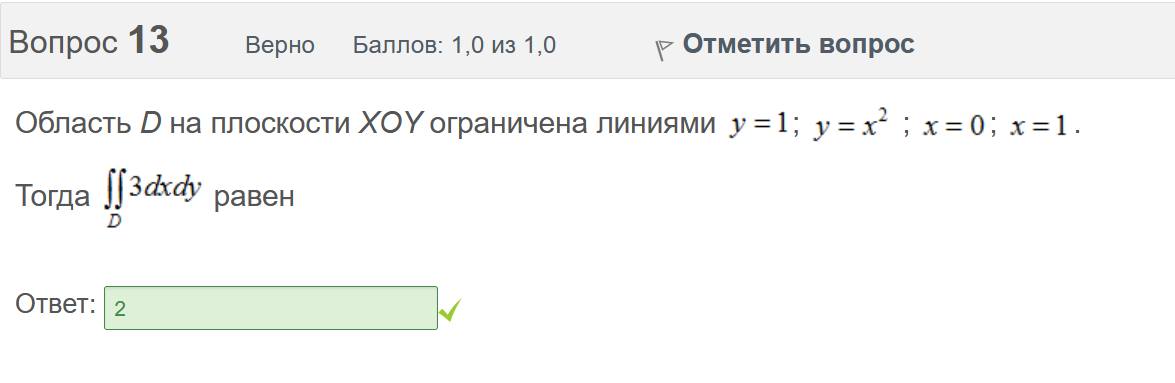Вопрос 14 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Для функции справедлива формула: Выберите один ответ:  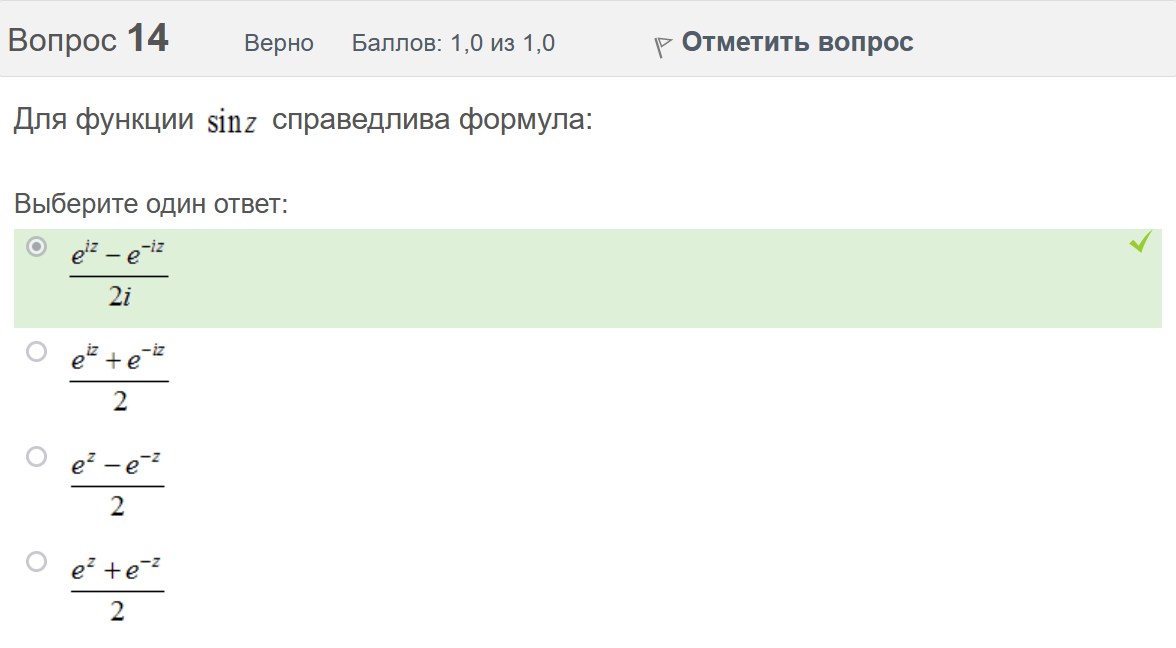Вопрос 15 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Общее решение дифференциального уравнения имеет вид: Выберите один ответ:  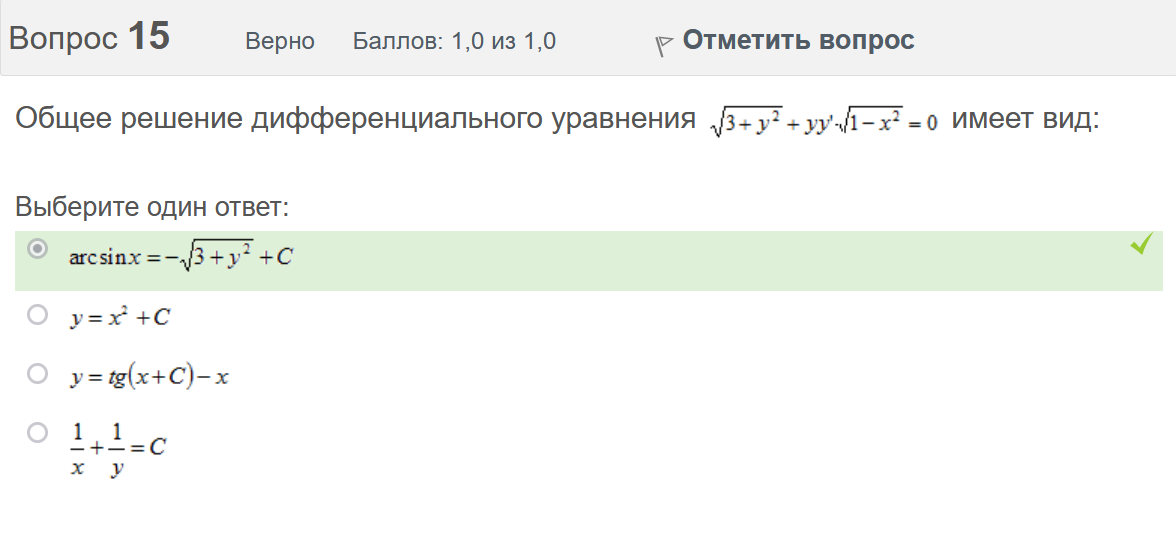Вопрос 16 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Решить уравнение . Выберите один ответ:  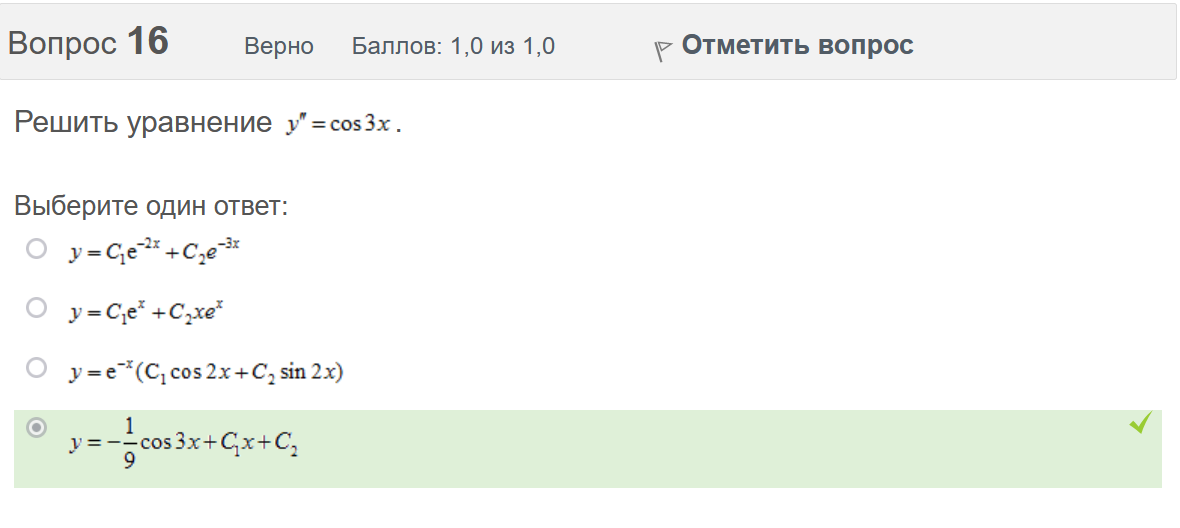Вопрос 17 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Найти cos(1 – i). Выберите один ответ:  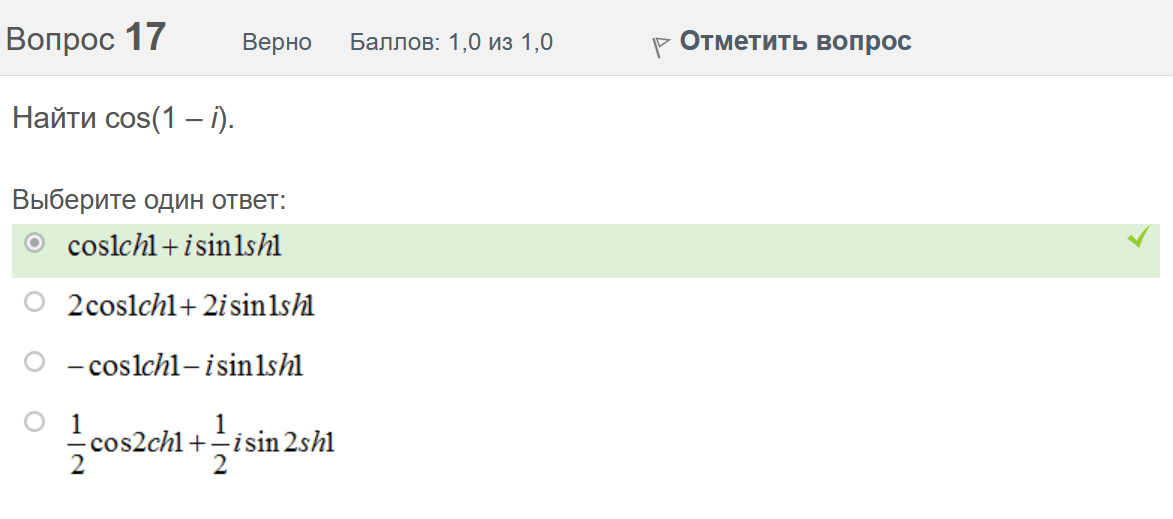Вопрос 18 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Методом Лагранжа можно решить Выберите один ответ: уравнение с разделяющимися переменными уравнение в полных дифференциалах линейное уравнение однородное уравнение Вопрос 19 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Главное значение аргумента комплексного числа равно: Выберите один ответ:  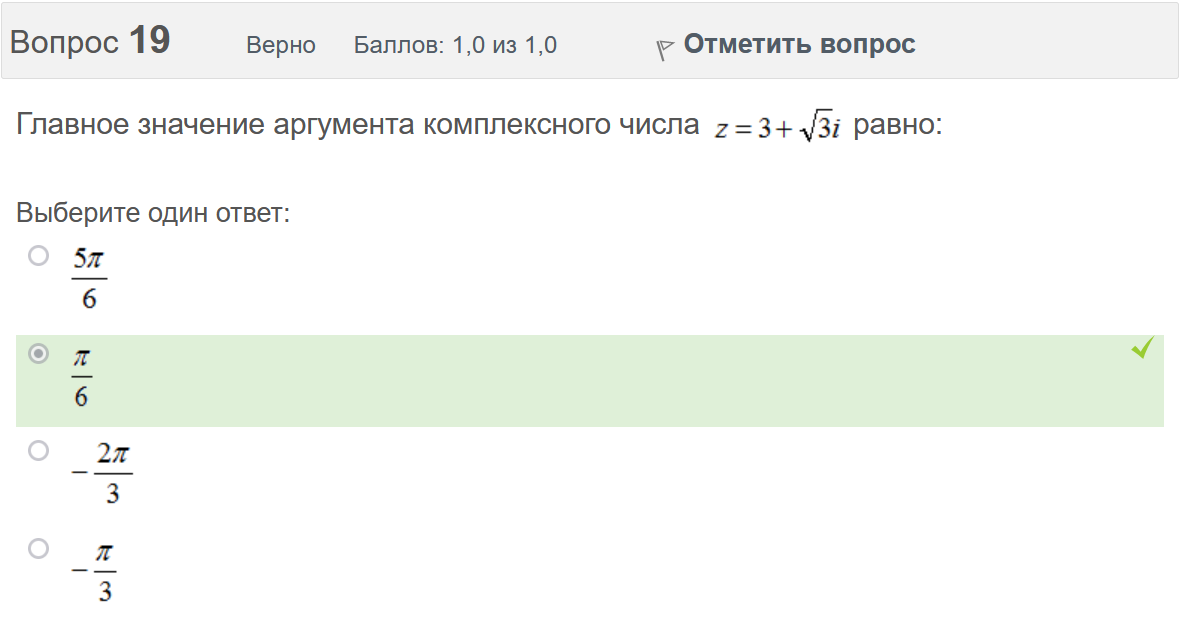Вопрос 20 Неверно Баллов: 0,0 из 1,0 Отметить вопросТекст вопроса Область D на плоскости XOY есть ΔАВС с вершинами A(0, 0), B(1, 2), C(1, 5). Тогда равен Ответ:  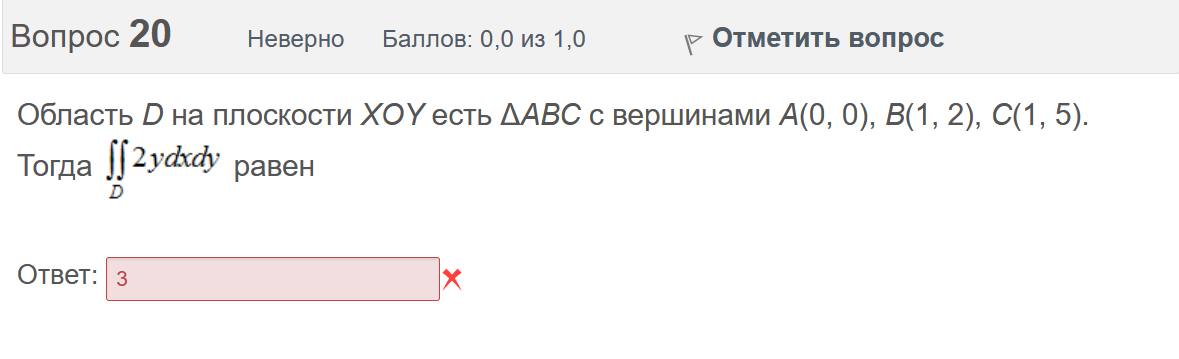Вопрос 21 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Уравнением Бернулли является Выберите один ответ:  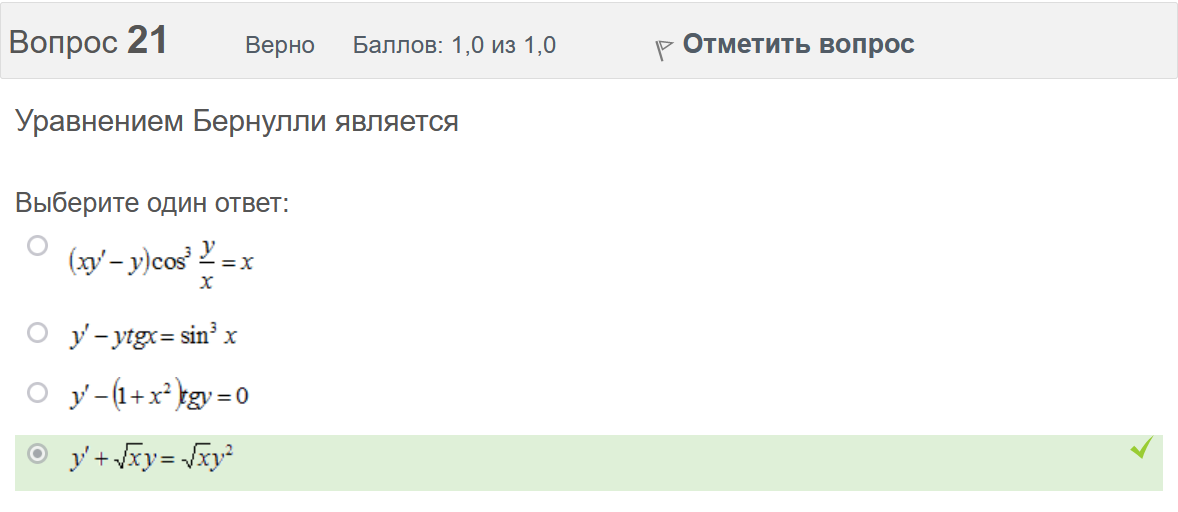Вопрос 22 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Найти cos(1 + i). Выберите один ответ:  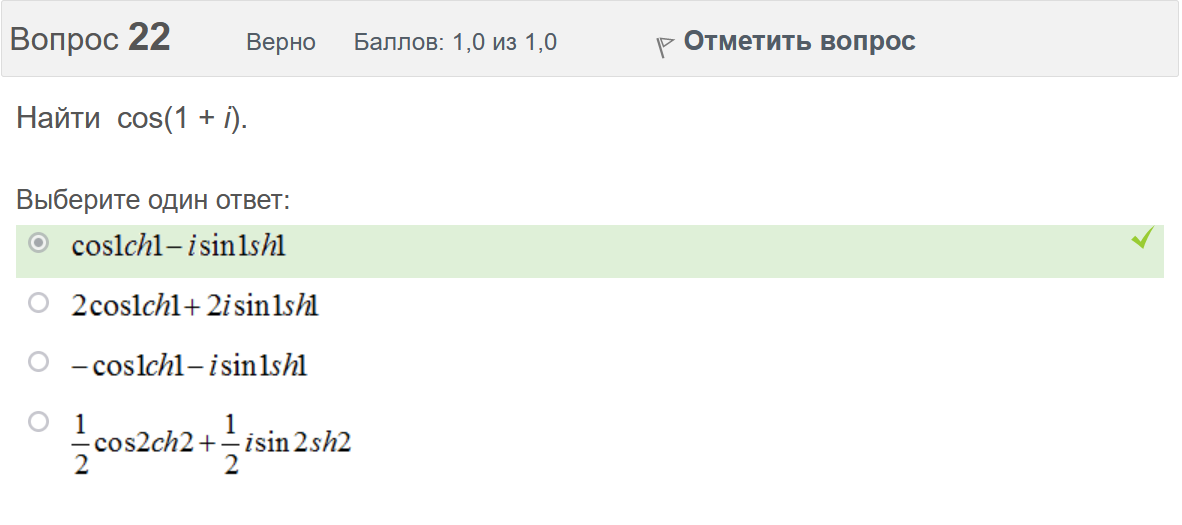Вопрос 23 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Среди предложенных функций выберите линейно независимую функцию для функции. Выберите один ответ:  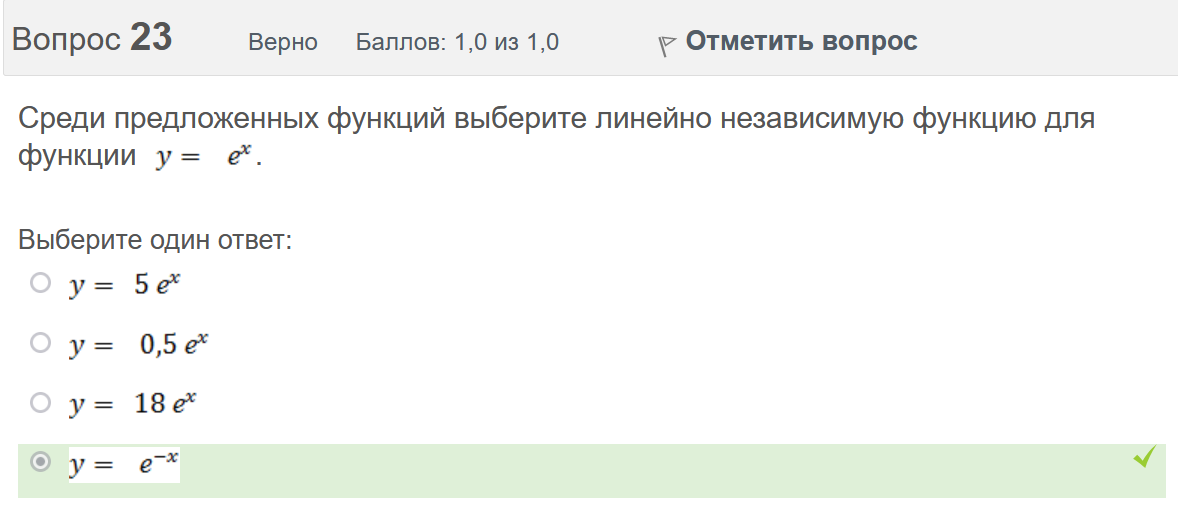Вопрос 24 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Даны линейные неоднородные дифференциальные уравнения второго порядка. Определите уравнение, которое является уравнением с правой частью специального вида. Выберите один ответ:  Вопрос 25 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Метод Лагранжа неопределенных коэффициентов применяется для решения линейных неоднородных дифференциальных уравнений 2 порядка. Для конструирования частного решения посредством анализа правой и левой частей уравнения необходимо знать величину r – кратность числа корней характеристического уравнения, равных . Даны линейные неоднородные дифференциальные уравнения 2 порядка с правой частью специального вида. Определите уравнения, которым соответствует r = 0. Выберите один или несколько ответов:  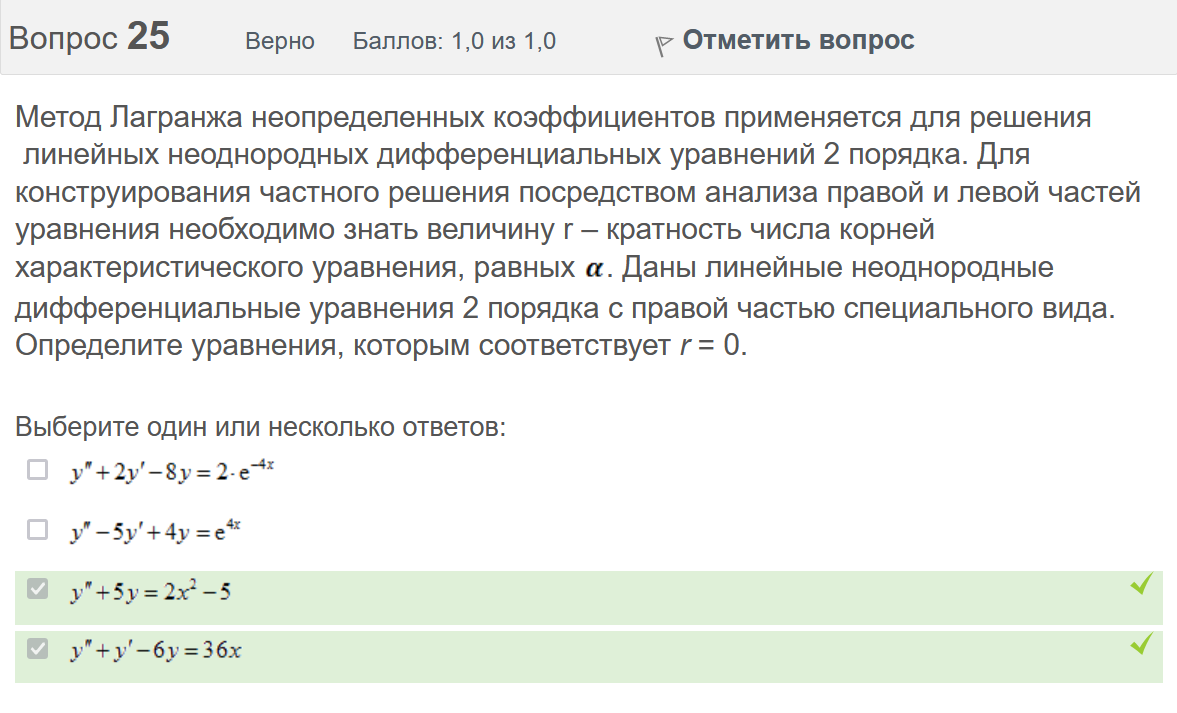Вопрос 26 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Даны линейные неоднородные дифференциальные уравнения второго порядка. Определите уравнения, которые можно решить методом Лагранжа неопределенных коэффициентов. Выберите один или несколько ответов:  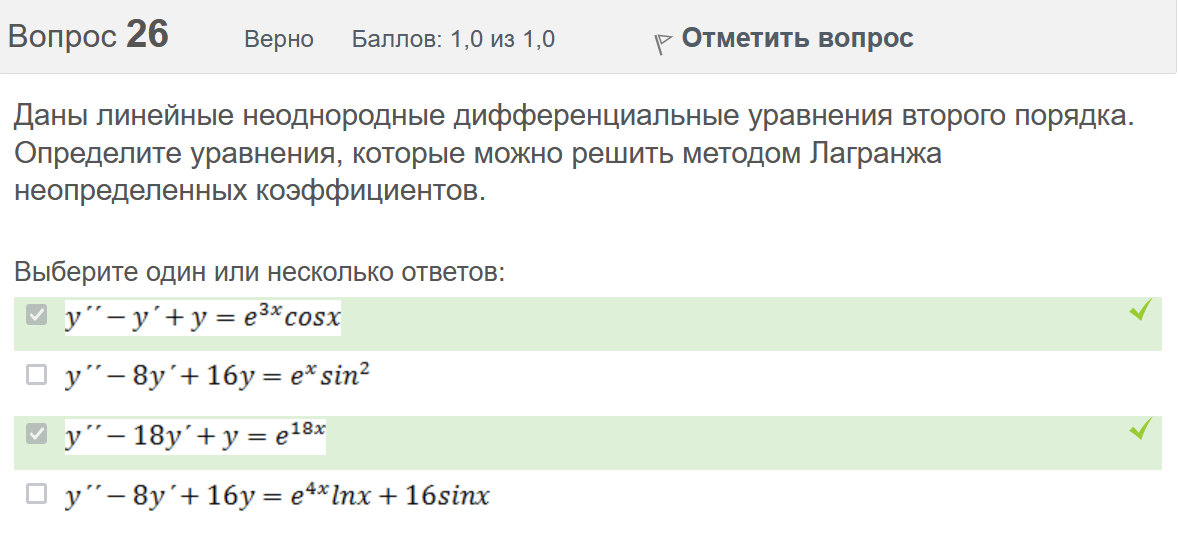Вопрос 27 Неверно Баллов: 0,0 из 1,0 Отметить вопросТекст вопроса Общее решение дифференциального уравнения имеет вид: Выберите один ответ:  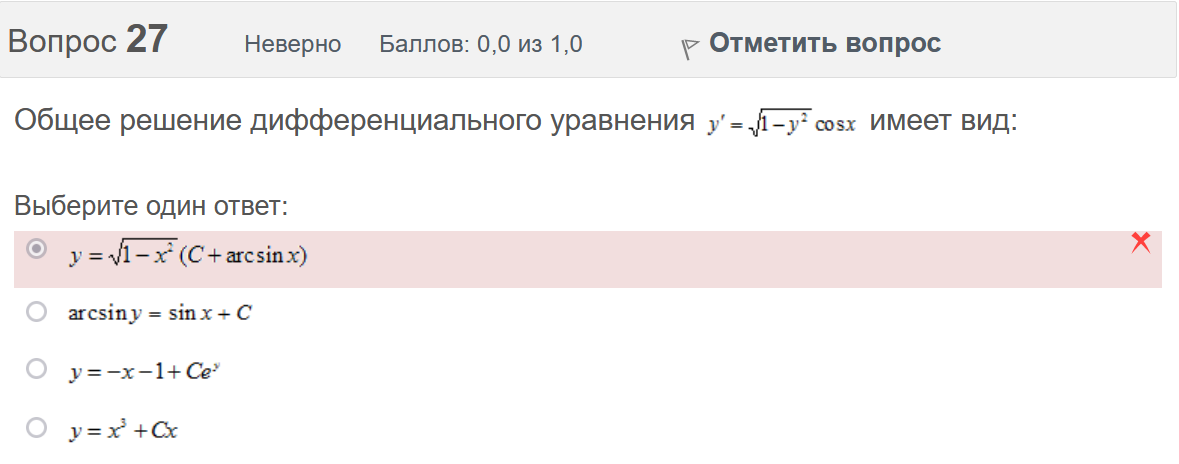Вопрос 28 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Записать в тригонометрической форме число 3i . Выберите один ответ:  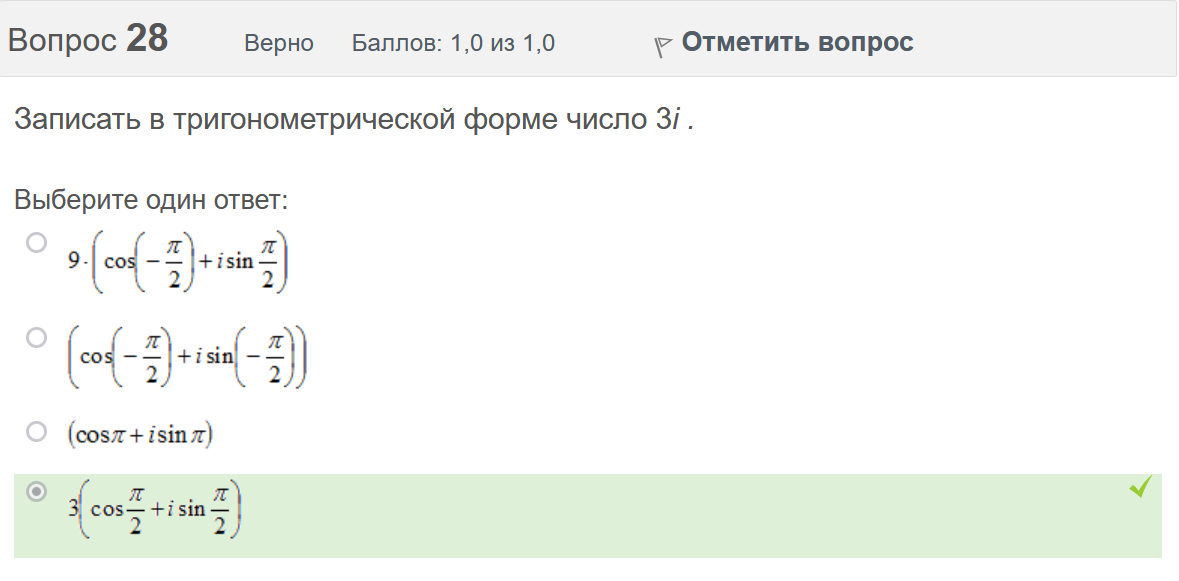Вопрос 29 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Область D на плоскости XOY ограничена линиями ; ; ; , плотность вещества на D – . Если yc есть y-координата центра масс области D, то равно Ответ:  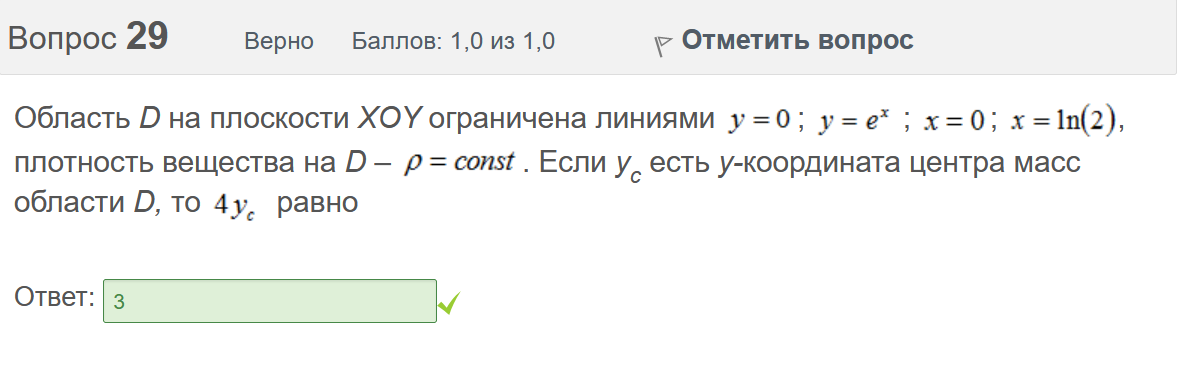Вопрос 30 Верно Баллов: 1,0 из 1,0 Отметить вопросТекст вопроса Область D на плоскости XOY ограничена линиями ; . Плотность вещества на D – . Тогда масса области D равна Ответ:  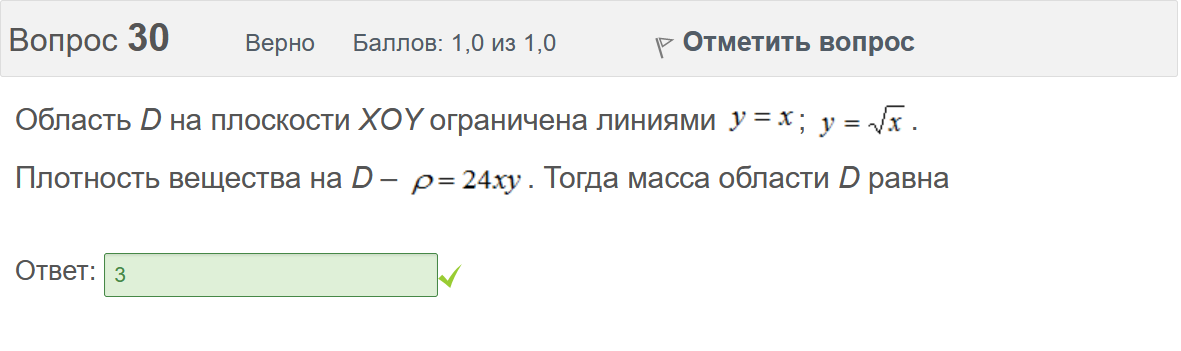Конец формыКонец формы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||