парная линейная регрессия. Парная линейная регрессия. Решение заданий высшей математики, экономики, бухучета
 Скачать 60.97 Kb.
|
|
Задача по эконометрике с решением. Выполнена в https://www.matburo.ru/ ©МатБюро – Решение заданий высшей математики, экономики, бухучета Решение задачи по эконометрике (парная регрессия)Задание Постройте поле корреляции результативного и факторного признаков. Определите параметры уравнения парной линейной регрессии. Дайте интерпретацию найденных параметров и всего уравнения в целом. Постройте теоретическую линию регрессии, совместив ее с полем корреляции. Сделайте выводы. Рассчитайте линейный коэффициент корреляции и поясните его смысл. Определите коэффициент детерминации и дайте его интерпретацию. С вероятностью 0,95 оцените статистическую значимость коэффициента регрессии и уравнения регрессии в целом. Сделайте выводы. С вероятностью 0,95 постройте доверительный интервал для прогноза оценки yi и доверительный интервал генерального значения ˆyген.( x = 5,75). Определите значение коэффициента эластичности и объясните его. Компания, занимающаяся продажей радиоаппаратуры, установила на видеомагнитофон определенной модели цену, дифференцированную по регионам. Следующие данные показывают цены на видеомагнитофон в 8 различных регионах и соответствующее им число продаж:
РешениеПостроим поле корреляции: 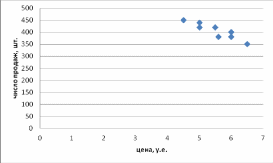 Очевидно, что число продаж видеомагнитофонов находится в обратной зависимости от установленных цен. Можно предположить, что зависимость линейная, так как расположение точек на графике по форме близко к прямой линии. Находим коэффициенты постулируемого уравнения регрессии, а также коэффициенты корреляции и детерминации. Для этого можно воспользоваться следующими формулами: yˆ x a bx b xy x* y  x2 (x)2a y bx Приведём расчётную таблицу:
Определим ряд характеристик моделируемых рядов: х у 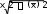   у2 ( у)2 0,61 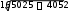 31,62х ∑(х х)2 2 * n 0,612 * 8 3 Рассчитаем коэффициенты регрессии: b 2214,74 5,51* 405 47,36 30,76 5,512 a 405 47,36 * 5,51 666,08 Таким образом, регрессионное уравнение имеет следующий вид: yˆx 666,08 47,36x Можно сделать вывод, что при росте цены на 1 у.е. число продаж видеомагнитофонов сокращается в среднем на 47,36 ≈ 47 шт. Условный объём продаж при нулевой цене равен 666 шт. Построим теоретическую линию регрессии: 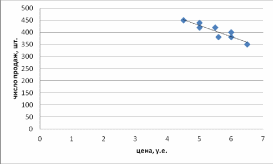 Так как эмпирические точки находятся вблизи теоретической прямой, то уравнение регрессии хорошо аппроксимирует данные. Определим линейный коэффициент корреляции: r xy x* y 2214,74 5,51* 405 0,919 x* y 0,61* 31,62 Коэффициент корреляции указывает на наличие связи и находится в интервале [-1;1]. В данном случае его отрицательное значение говорит об обратной связи между ценой видеомагнитофона и объёмом продаж. Связь весьма высокая по тесноте, так как |r| > 0,9. Рассчитаем коэффициент детерминации: R2 1 ∑( y yˆх ) 2  ∑( y y)2 1 1250,93 8000 0,844 Коэффициент детерминации показывает, что 84,4% вариации числа продаж видеомагнитофонов объясняется вариацией их цен, а остальные 15,6% - вариацией прочих факторов. 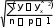 На основании данных расчётной таблицы рассчитаем остаточное среднее квадратическое отклонение:Sост , где 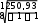 р – число факторов в модели.Sост 14,44 Определим стандартную ошибку для коэффициента регрессии: mb S ост * 14,44 * 8,32  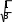 Определим расчётное значение t-критерия Стьюдента:t b 47,36 5,69 m b b8,32 Табличное значение t-критерия Стьюдента при α = 0,05 и k = 8 – 1 – 1 = 6 будет равно tтабл = 2,45. Таким образом, коэффициент регрессии оказался значим, так как расчётное значение t-критерия по модулю выше табличного значения. Для определения значимости полученного уравнения регрессии необходимо рассчитать эмпирическую величину F-критерия Фишера: R2 Fp 1 R2 * n p 1 p 0,844 * 1 0,844 8 1 1 1 32,37 По таблице F-распределения Снедекора-Фишера при α = 0,05 и К1 = 1, К2 = 8 – 2 = 6 величина Fт = 5,99. Это означает, что гипотеза Н0 о несущественности связи между y и x с вероятностью ошибочности суждения α = 0,05 отклоняется, то есть связь между этими переменными может быть признана существенной. Спрогнозируем число продаж видеомагнитофонов при цене 5,75 у.е. за 1 шт. yˆxр 666,08 47,36 * 5,75 393,75 Построим доверительные интервалы для индивидуальной прогнозной величины точке х* по следующим формулам: yˆxр dy yˆxр yˆxр dy, где yˆ xр в  dy tтабл * Sост *, где h 1 n (x* x)2  ∑(x x)2 1 8 (5,75 5,51) 2 3 0,14 Тогда: dy 2,45 *14,44 *  1 0,14 37,79393,75 37,79 yˆxр 393,75 37,79 355,97 yˆxр 431,54 Следовательно, с 95% уверенностью можно утверждать, что число продаж видеомагнитофонов компанией при цене 5,75 у.е. за 1 шт., находится в пределах от 356 до 431 шт. Если нужно сделать вывод относительно числа продаж во всех компаниях со средней ценой видеомагнитофона 5,75 у.е., то необходимо построить доверительный интервал для генерального среднего значения ˆyген. при заданном х*. Вариация в этом случае будет 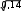 меньше, поскольку имеет место не отдельное, а со среднее значение у. Следовательно, интервал будет уже: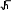 dy tтабл * Sост * 2,45 *14,44 * 13,4 393,75 13,4 yˆген 393,75 13,4 380,36 yˆген 407,15 Таким образом, с 95% уверенностью можно утверждать, что число продаж видеомагнитофонов во всех компаниях по средней цене 5,75 у.е. находится в пределах от 380 до 407 шт. Коэффициент эластичности определим по формуле:  Э b* x (47,36) *yx y 0,61 31,62 0,64% Итак, в относительном выражении при увеличении цены видеомагнитофона на 1% возможно сокращение продаж в анализируемой компании на 0,64%. |