Моделирование практическая 3. Моделирование в среде табличного процессора
 Скачать 119.5 Kb.
|
|
Практическая работа Тема: Моделирование в среде табличного процессора. Цель: Демонстрация возможностей моделирования в среде табличного процессора MS Excel. Развитие творческих способностей у учащихся. Анализ объекта: Компьютерная модель в среде MS Excel. Задача. Падение с лестницы. Электрик Петров приставил к стене лестницу длины L, имеющую 10 ступенек, и, поднявшись вверх, остановился на одной из ступенек. В это время концы лестницы начали скользить вдоль стены и пола. Провести исследование, по какой кривой будет падать электрик Петров в зависимости от того, на какой ступеньке он стоит. Математическая модель: Обозначим: L – длина лестницы; N – число ступенек лестницы (по условию задачи N =10); k – номер ступеньки, на которой стоит электрик и для которой ведется расчет траектории движения. Для определенности считаем, что ступеньки пронумерованы от 1 до N, начиная снизу. Будем считать, что лестница первоначально занимала вертикальное положение. Это не совсем реально, но удобно для дальнейших расчетов. При скольжении концов лестницы координата y конца A изменяется от L до 0, координата x = 0 всегда. А для конца B наоборот – координата x изменяется от 0 до L, а y = 0. У промежуточных точек изменяются обе координаты. В 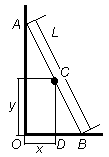 ычислим координаты ступеньки с номером k (см. рисунок). 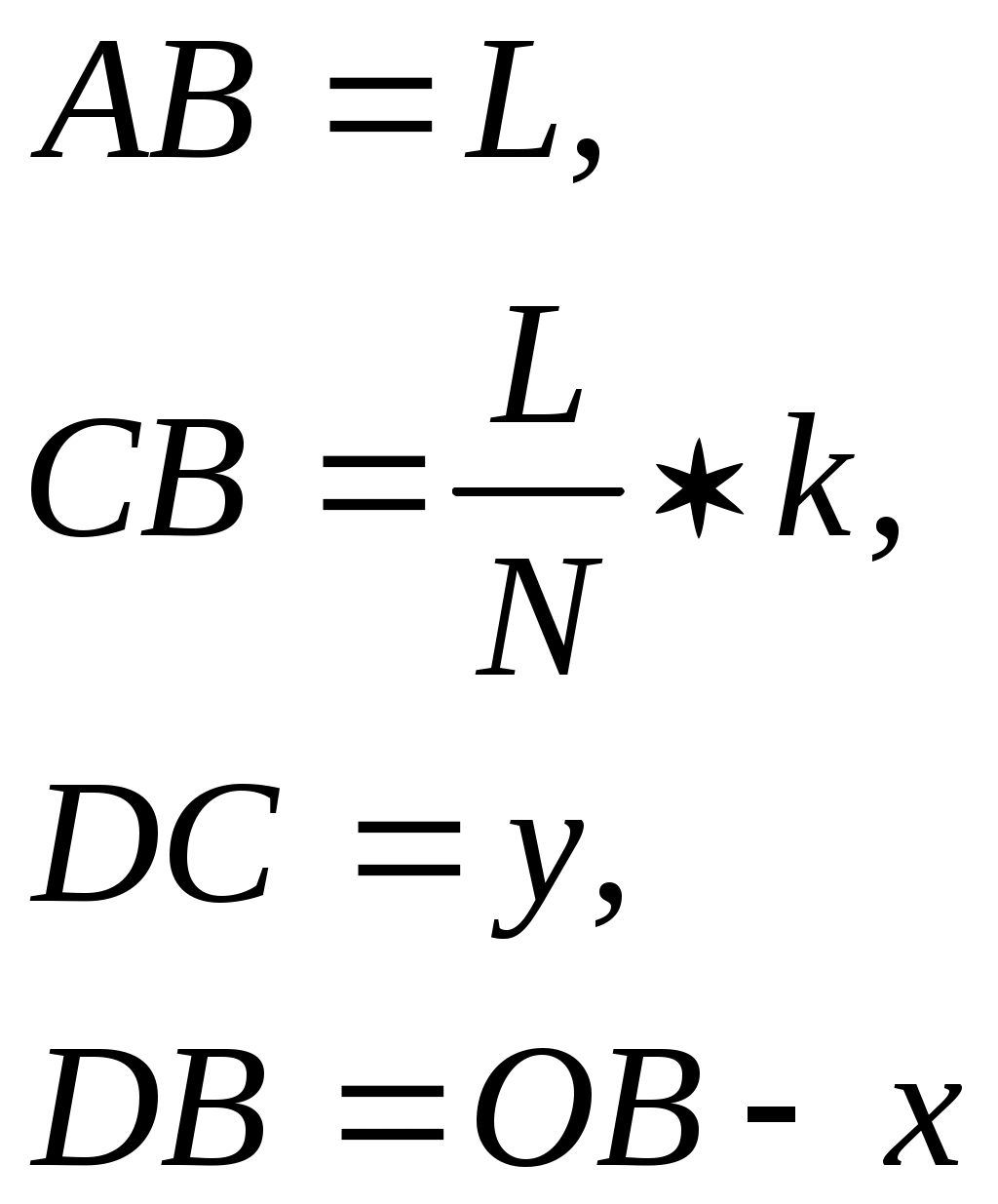Из рисунка можно заметить, что треугольники OAB и DCB подобны, поэтому их стороны пропорциональны: , при этом  Используя эти выражения, получаем:  .Из это пропорции можно получить формулы для координат k-й ступеньки:  (1)  (2)Расстояния OA и OB связаны с теоремой Пифагора:  Из этой формулы можно выразить OA через OB:  , или наоборот. (3)Траекторию движения ступеньки с электриком будем строить поточечно. Обозначим M – количество точек расчета. В дальнейшем будем вычислять координаты ступеньки для положений лестницы, при которых нижний конец – точка B – перемещается на одну и ту же величину  . Изменяя координату x точки B от 0 до L с шагом  , вычисляем длину отрезка OA по формуле (3), а затем координаты ступеньки по формулам (1) и (2).Задание: Составьте компьютерную модель, проведите расчет координат положения электрика в зависимости от положения лестницы. Пример заполнения электронной таблицы:
По результатам вычислений по столбцам C и D постройте диаграмму кривой, по которой движется ступенька с электриком. Убедитесь, что эта кривая похожа на четверть эллипса, сплющенного либо к оси ординат (если номер ступеньки >5), либо к оси абсцисс (если номер ступеньки <5). А на что похожа кривая, если номер ступеньки =5? Проведите расчет и постройте общую диаграмму кривых для всех ступенек. Для построения общей диаграммы надо скопировать результаты проведения экспериментов в соседние столбцы. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||