высшая математика. 10 Обыкновенные диф-ые ур-ия. Контрольная работа. Контрольная работа 10 Обыкновенные дифференциальные уравнения. Задачи 112
 Скачать 1.81 Mb.
|
|
Контрольная работа № 10 Обыкновенные дифференциальные уравнения. ЗАДАЧИ № 1-12 Задачи № 1-№ 5. Уравнения первого порядка: с разделяющимися переменными и приводящиеся к ним, однородные и приводящиеся к однородным, линейным уравнения, уравнение Бернулли, уравнение в полных дифференциалах. Задача № 6. Смешанные задачи на д.у. первого порядка. Определить тип уравнения и указать в общем виде метод решения. Задача № 7. Смешанные задачи на д.у. первого порядка. Определить тип уравнения и решить. Задача № 8. Уравнения, допускающие понижение порядка. Задача № 9. Однородные линейные д.у. второго и высших порядков. Задача № 10 - №11. Неоднородные линейные уравнения с постоянными коэффициентами с правой частью специального вида. Задача № 12. Метод Лагранжа, метод вариации постоянных. Задача № 1. Уравнения с разделяющимися переменными и приводящиеся к ним. Дифференциальное уравнение  называется уравнением с разделенными переменными, его общий интеграл имеет вид .Уравнение  , в котором коэффициенты при дифференциалах распадаются на множители, зависящие только от  и только от  называется уравнением с разделяющимися переменными.Путем деления на произведение  оно приводится к уравнению с разделенными переменными: .Общий интеграл этого уравнения имеет вид  .Замечание. Деление на  может привести к потере частных решений, обращающих в ноль произведение .Дифференциальное уравнение  , где  - постоянные, заменой переменных  преобразуется в уравнение с разделяющимися переменными. Пример 1. Решить уравнение  Решение. Разделим обе части уравнения на произведение   .Получим уравнение с разделенными переменными. Интегрируя его, найдем  .После потенцирования получим  или  .Откуда  .Обозначая  , будем иметь  или  .Получили общий интеграл этого уравнения. Функции  ,  и  - являются частными решениями.Ответ:  - общий интеграл.Пример 2. Найти частное решение уравнения 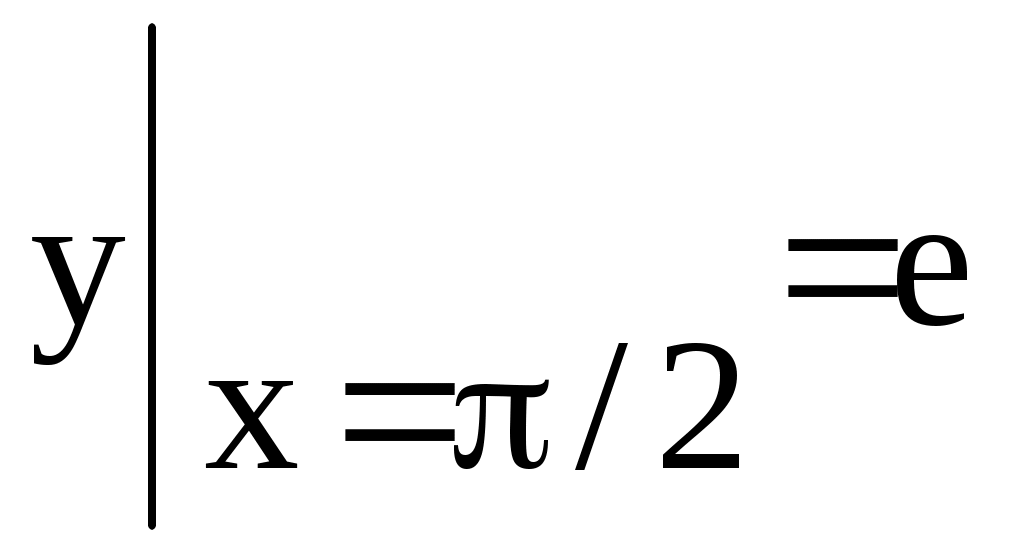 , удовлетворяющее начальному условию  .Решение. Имеем  или  .Разделяем переменные, для этого обе части уравнения делим на произведение   .Интегрируя, найдем общий интеграл  в качестве производной константы  взяли  .После потенцирования, получим  или  - общее решение исходного уравнения.Найдем константу , используя начальное условие  ,  или отсюда  .Искомое частное решение или решение задачи Коши  .Ответ: .Упражнения. Решить уравнения 1.  . Ответ:  .2.  . Ответ:  .3.  . Ответ:  .4.  . Ответ:  или  .Контрольное задание № 1. Решить уравнения Решить уравнения с разделяющимися переменными:
Задача 2. Однородные дифференциальные уравнения. Дифференциальное уравнение (д.у.)  Называется однородным д.у. относительно и , если функция  является однородной функцией своих аргументов нулевого измерения. Это значит  . Например функция  - однороднаяфункция нулевого измерения. Однородное д.у. всегда можно представить в виде  (1)Введя новую искомую функцию  , уравнение (1) можно привести к уравнению с разделяющимися переменными:   или  переменные разделяются.Пример 3. Решить уравнение  .Решение. Запишем уравнение в виде  , разделив на обе части уравнения. Сделаем замену  . Тогда  ,  . Получим  или  .Разделяя переменные, будем иметь  .Отсюда интегрированием находим   или , так как  , то обозначая  , получим . Заменяя  на  , будем иметь общий интеграл , отсюда  - общее решение.Ответ: .Упражнения. Решить уравнения 1.  . Ответ:  .2.  . Ответ:  .3.  . Ответ:  .4.  . Соберем коэффициенты при   . Ответ:  . |
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.