высшая математика. 10 Обыкновенные диф-ые ур-ия. Контрольная работа. Контрольная работа 10 Обыкновенные дифференциальные уравнения. Задачи 112

• Название: Контрольная работа 10 Обыкновенные дифференциальные уравнения. Задачи 112
• Анкор: высшая математика
• Дата: 25.12.2022
• Размер: 1.81 Mb.
• Имя файла: 10 Обыкновенные диф-ые ур-ия. Контрольная работа.doc
• Тип: Контрольная работа; #863700
• страница: 5 из 7

Пример 10. Решить уравнение .

Решение.

Данное уравнение III типа. Введем обозначение 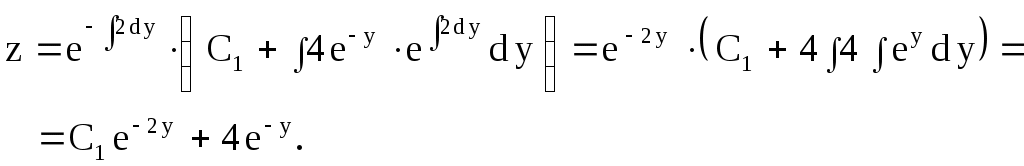, получим - уравнение Бернулли. Подстановкой оно сводится к линейному уравнению .



Заменяя на , получим . Интегрируя, будем иметь

или ; .

Замечание. При решении задачи Коши для уравнений высших порядков целесообразно определять значения постоянных в процессе решения, а не после нахождения общего решения уравнения.

Пример 11. Решить задачу Коши .

Решение.

Полагая , получим или откуда ; .

Разделяя переменные, найдем . Интеграл в правой части в элементарных функциях не вычисляется, как интеграл от дифференциаль-

ного бинома, случай неберущегося интеграла.

Но если использовать начальные условия , то и тогда



Ответ: .

Упражнения. Решить уравнения.

1) 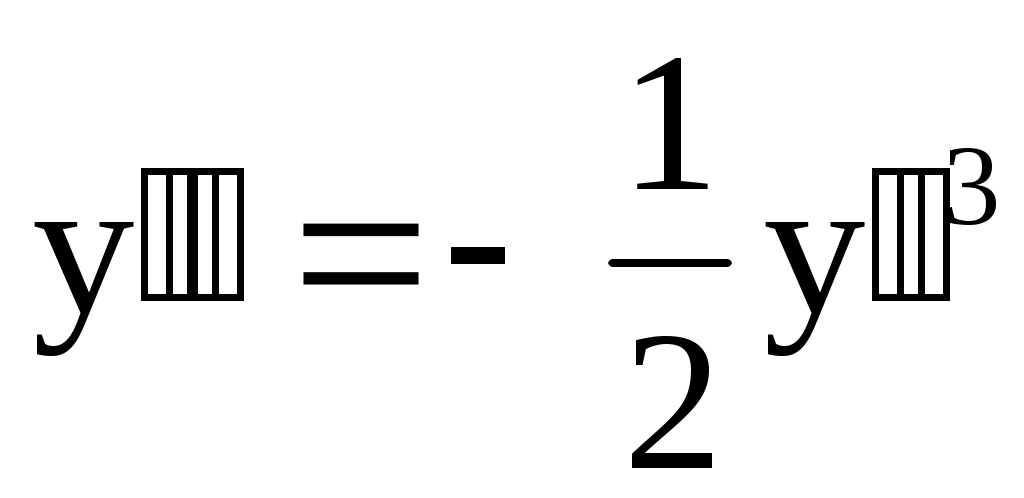. Ответ: .

2) . Ответ: .

3) . Ответ: .

4) . Ответ: .
Контрольное задание № 8.

Решить уравнения, допускающие понижение порядка

1.	.
2.	.
3.	.
4.	.
5.	.
6.	.
7.	.
8.	.
9.	.
10.	.
11.	.
12.	.
13.	.
14.	.
15.	.
16.	.
17.	.
18.	.
19.	.
20.	.
21.	.
22.	.
23.	.
24.	.
25.	.
26.	.
27.	.
28.	.
29.	.
30.	.

Задача 9. Линейные дифференциальные уравнения 2– го и n–го порядка.

Линейные однородные уравнения с постоянными коэффициентами.

Рассмотрим дифференциальное уравнение

, (1)

где - вещественные постоянные числа. Решение уравнения (1) находим в виде

- подстановка Эйлера (2)

- неизвестная постоянная. Подставляя (2) в (1), получим уравнение

, (3)

которому удовлетворяет .

Уравнение (3) называется характеристическим уравнением.

Пусть - корни уравнения (3), причем среди них могут быть и кратные.

Возможны следующие случаи:

1) - вещественные и различные

Тогда фундаментальная система решений уравнения (1) имеет вид и общим решением искомого уравнения будем

.

2) Корни характеристического уравнения вещественные, но среди них есть кратные. Пусть, например,

, т. е. – является – кратным корнем уравнения (3), а остальные корнем различные.

Фундаментальная система решений в этом случае имеет вид

,

а общее решение

.

3) среди корней характеристического уравнения есть комплексные числа.

Пусть для определенности

,

А остальные корни вещественные (комплексные корни попарно сопряженные, т. к. по предположению коэффициенты уравнения (3) – вещественные).

Фундаментальная система решений имеет вид





а общее решение



4) в случае, если является – кратным корнем уравнения (3), то также будет – кратным корнем и фундаментальная система решений будет иметь вид



а общее решение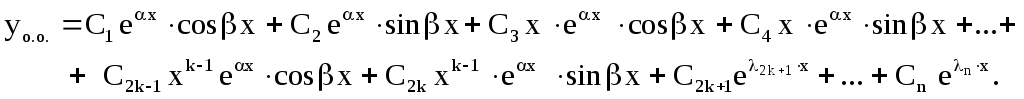


Пример 12. Найти общее решение уравнения .

Решение.

Составляем характеристическое уравнение .

Находим . Так как все они действительные и различные, то общее решение имеет вид .

Пример 13. Найти общее решение уравнения .

Решение.

Характеристическое уравнение имеет вид

.

Отсюда . Корни вещественные, причем один из них – двукратный, поэтому общее решение имеет вид

.

Пример 14. Решить уравнение .

Решение.

Характеристическое уравнение имеет корни , , .

Общее решение

.

Пример 15. Решить уравнение .

Решение.

Характеристическое уравнение или имеет корни – однократный и – пара двукратных

мнимых корней. Общее решение

.

Упражнения. Проинтегрировать следующие однородные линейные уравнения.

1) . Ответ: .

2) . Ответ: .

3) . Ответ:

.

4) Ответ: ,

. .