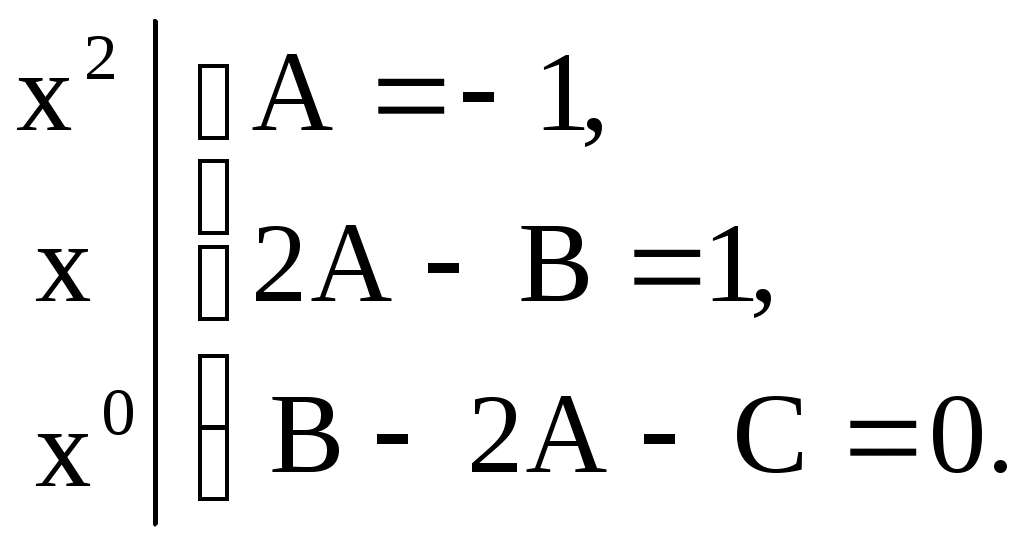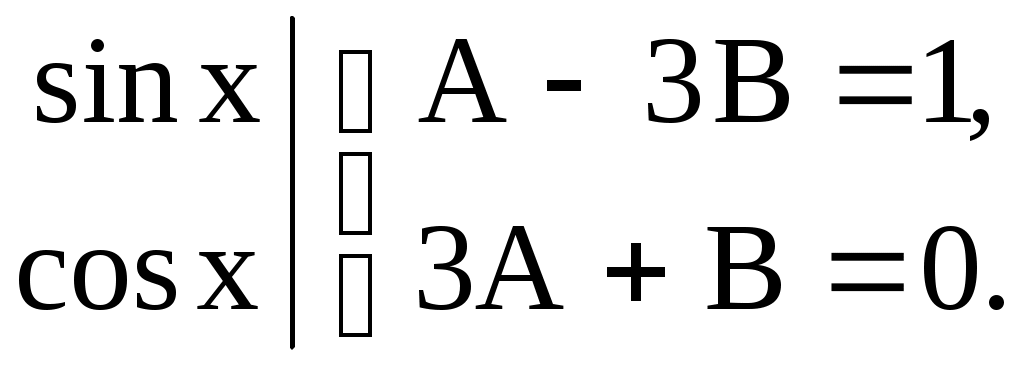|
|
высшая математика. 10 Обыкновенные диф-ые ур-ия. Контрольная работа. Контрольная работа 10 Обыкновенные дифференциальные уравнения. Задачи 112
Контрольное задание № 9.
Решить однородные дифференциальные уравнения с постоянными коэффициентами:
-
1.
|
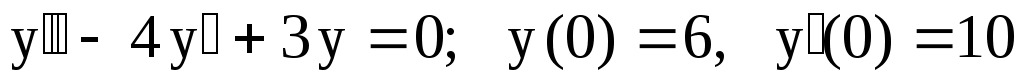 . .
|
2.
|
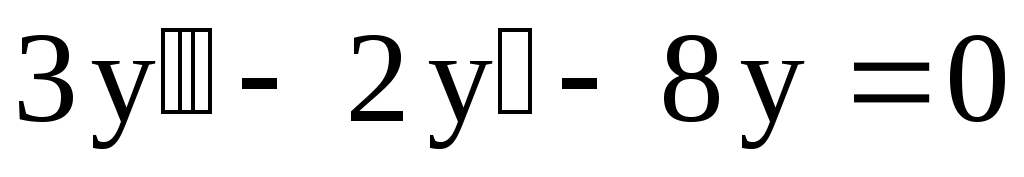 . .
|
3.
|
 . .
|
4.
|
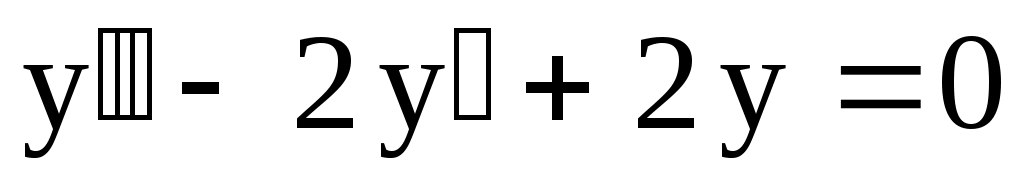 . .
|
5.
|
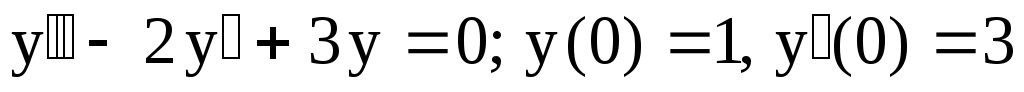 . .
|
6
|
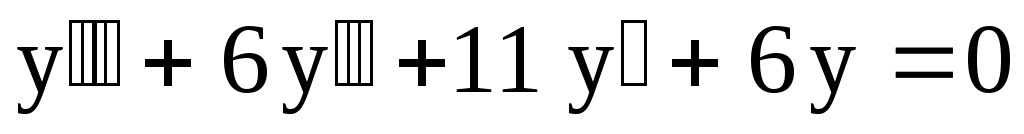 . .
|
7.
|
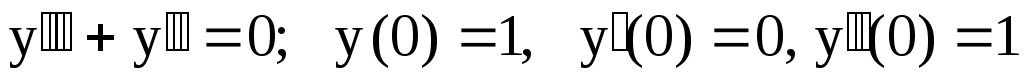 . .
|
8.
|
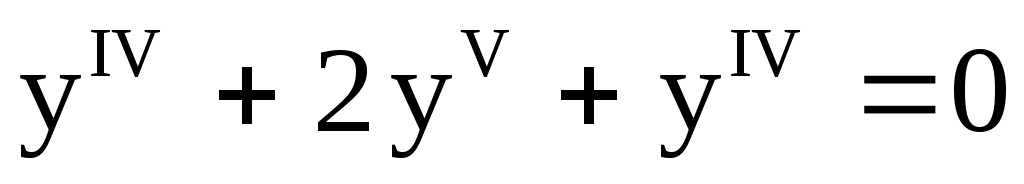 . .
|
9.
|
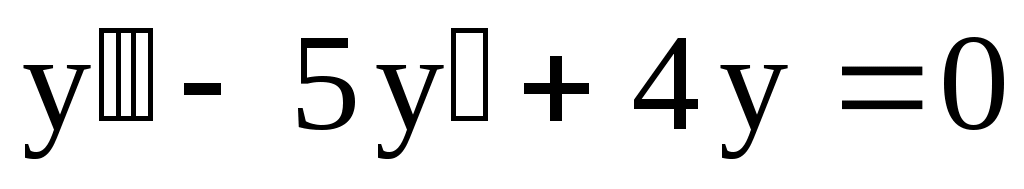 . .
|
10.
|
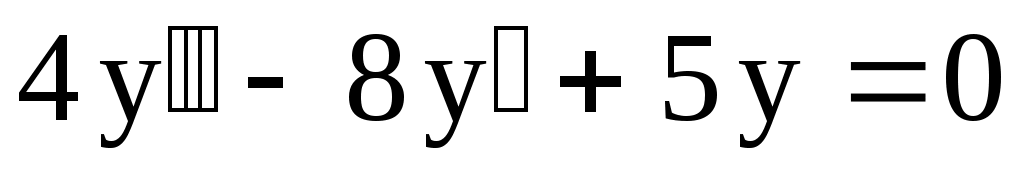 . .
|
11.
|
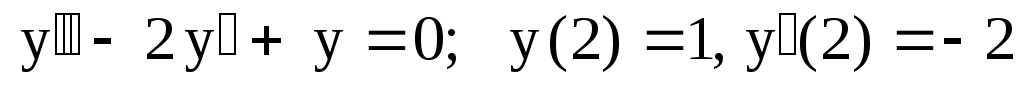 . .
|
12.
|
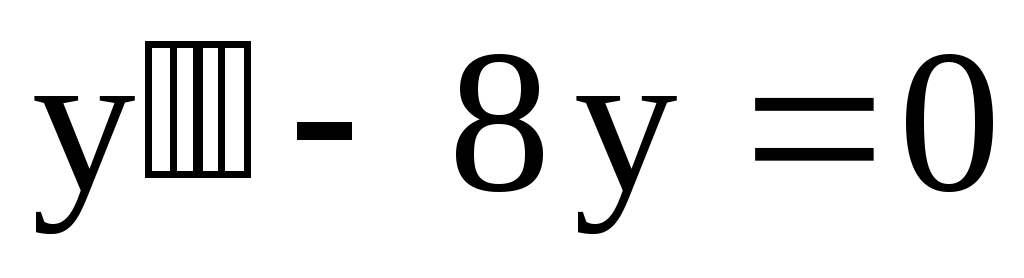 . .
|
13.
|
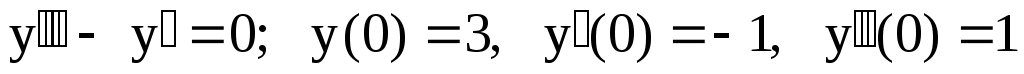 . .
|
14.
|
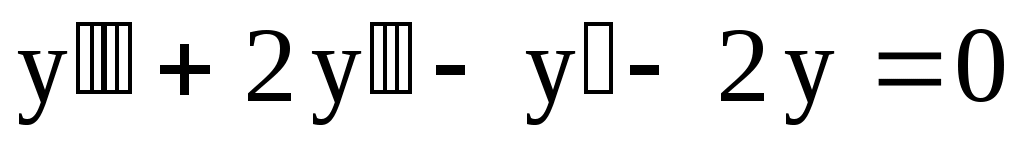 . .
|
15.
|
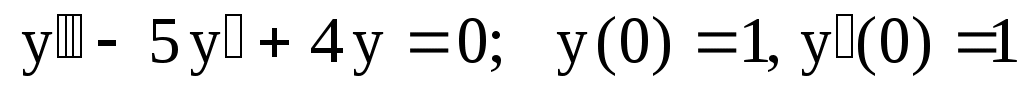 . .
|
16.
|
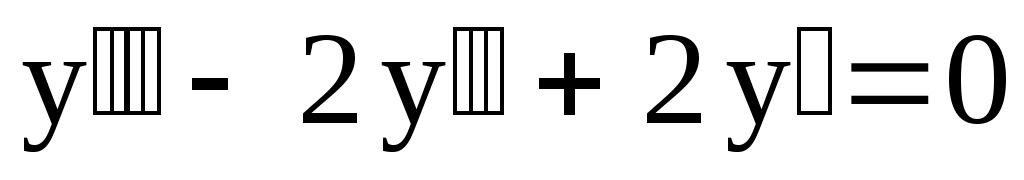 . .
|
17.
|
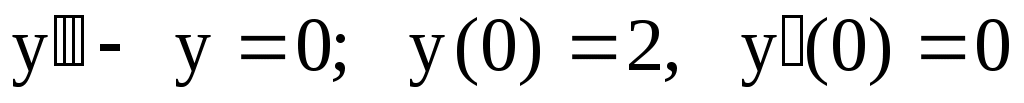 . .
|
18.
|
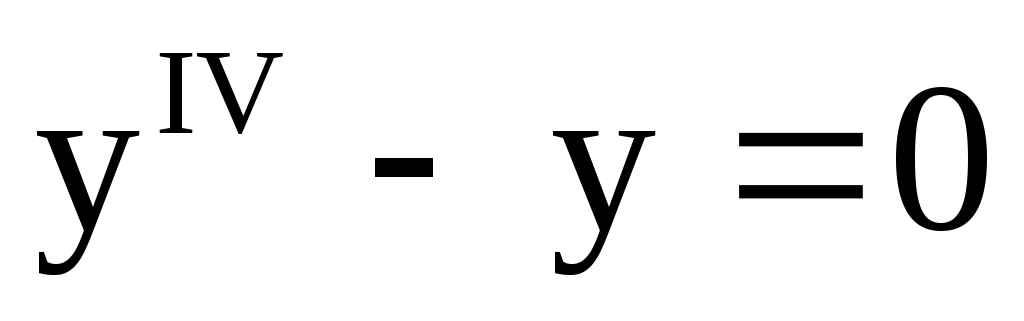 . .
|
19.
|
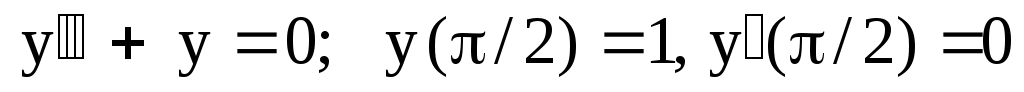 . .
|
20.
|
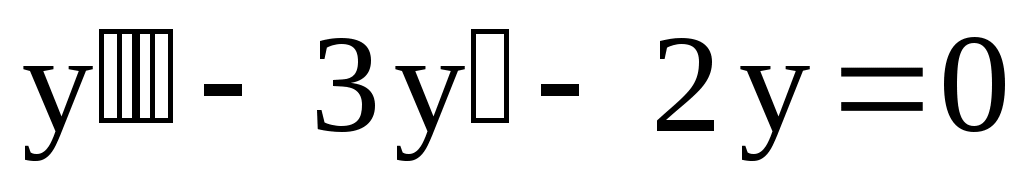 . .
|
21.
|
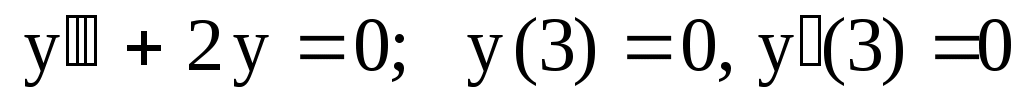 . .
|
22.
|
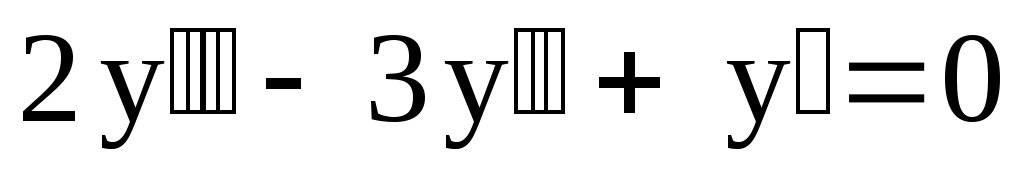 . .
|
23.
|
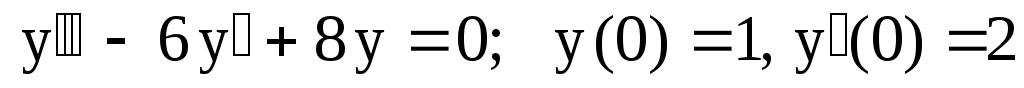 . .
|
24.
|
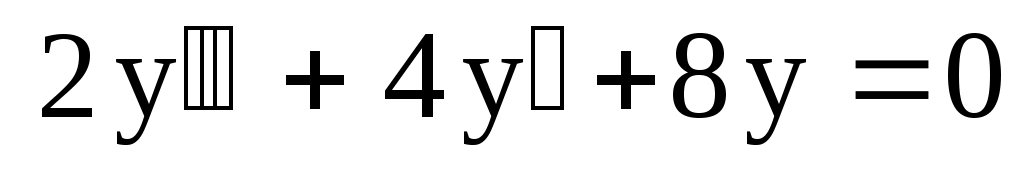 . .
|
25.
|
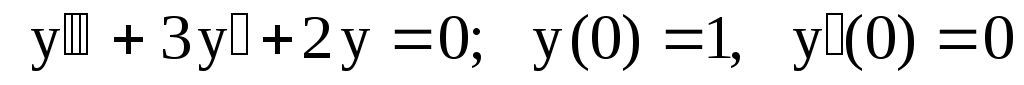 . .
|
26.
|
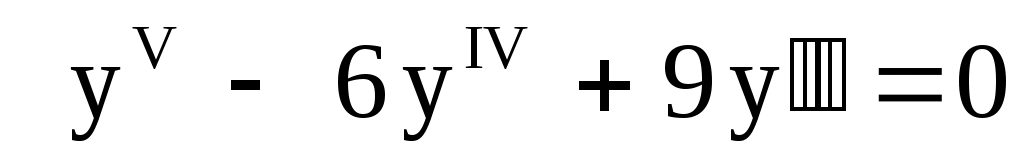 . .
|
27.
|
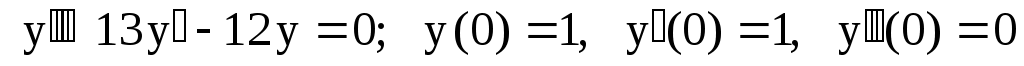 . .
|
28.
|
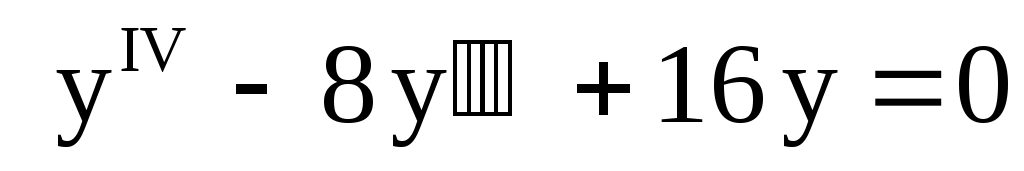 . .
|
29.
|
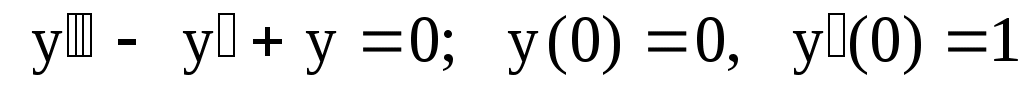 . .
|
30.
|
 . .
|
Указание. Воспользоваться формулой извлечения корня 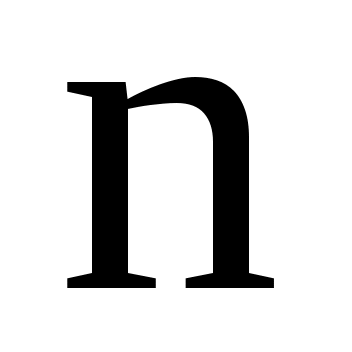 –й степени из комплексного числа –й степени из комплексного числа
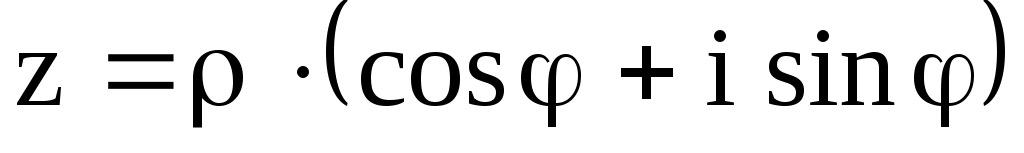 , ,
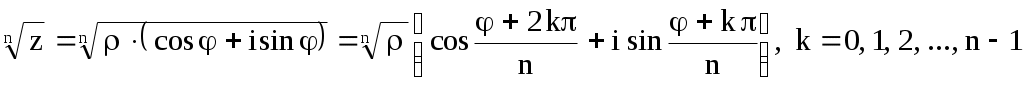 . .
Задача 10. Линейные неоднородные уравнения с постоянными коэффициентами и с правой частью специального вида. Метод подбора или метод неопределенных коэффициентов.
Дано уравнение
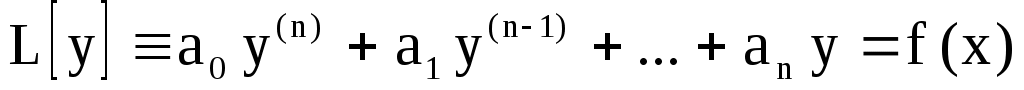 (1) (1)
С постоянными вещественными коэффициентами 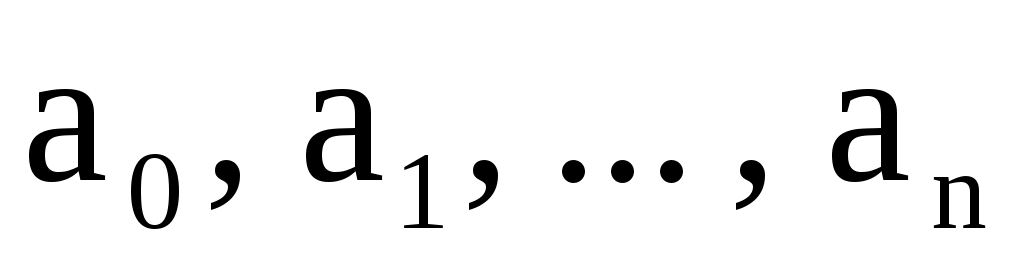 . .
Общее решение неоднородного уравнения или уравнения с правой частью 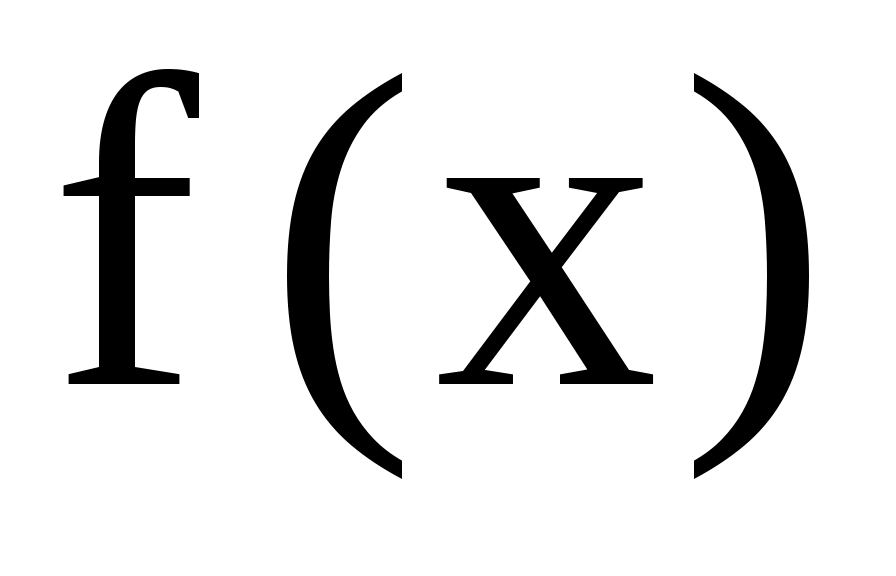 равно сумме общего решения соответствующего однородного уравнения и какого-либо частного решения неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и какого-либо частного решения неоднородного уравнения 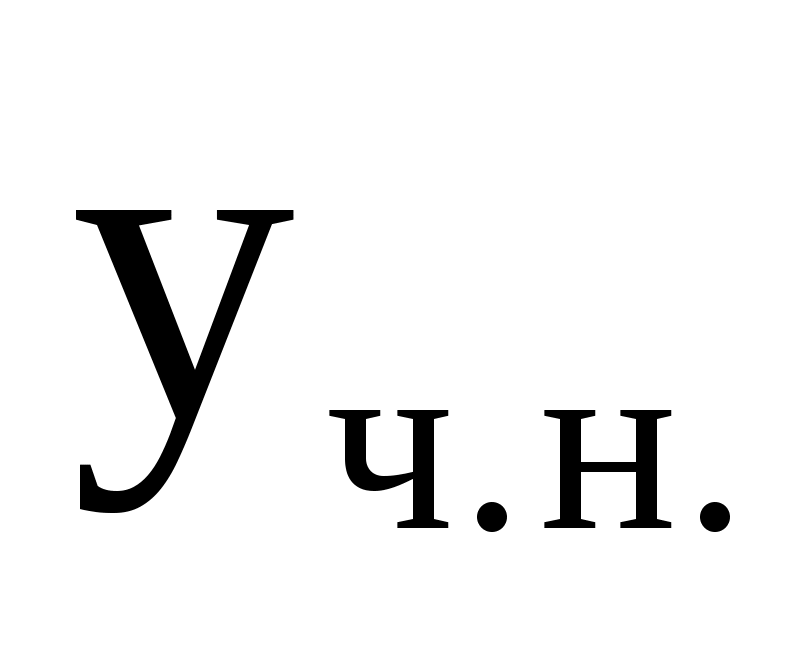
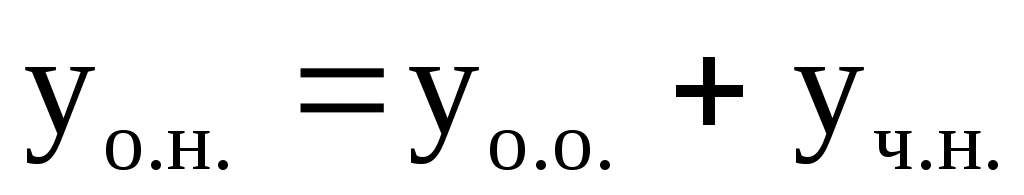 . .
Для правых частей специального вида частное решение можно найти так называемым методом подбора.
Общий вид правой части 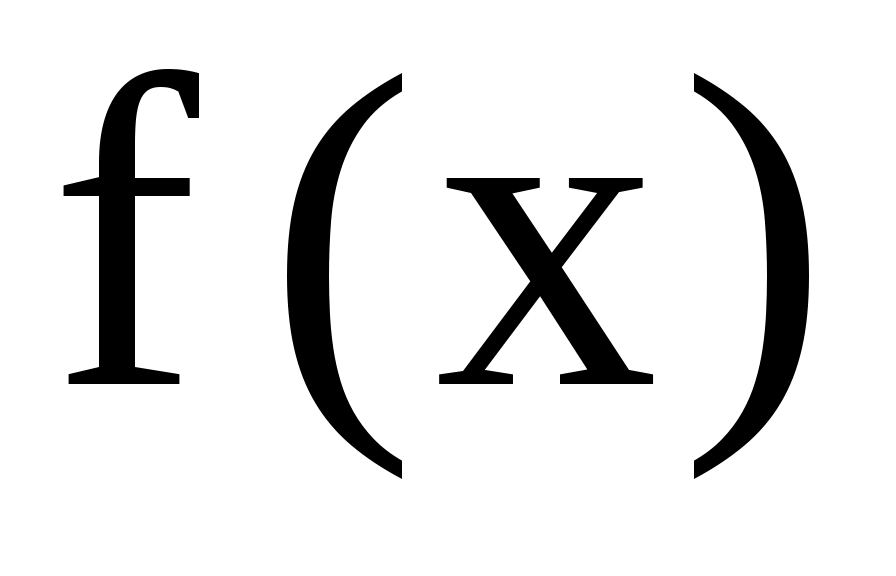 уравнения (1), при котором возможно применить метод подбора, следующий: уравнения (1), при котором возможно применить метод подбора, следующий:
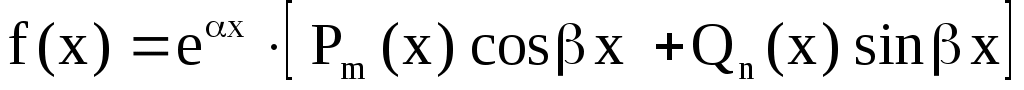 (2), (2),
где 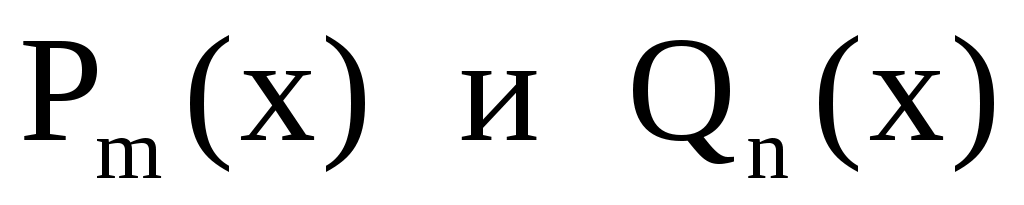 многочлены степени многочлены степени  соответственно. соответственно.
В этом случае частное решение 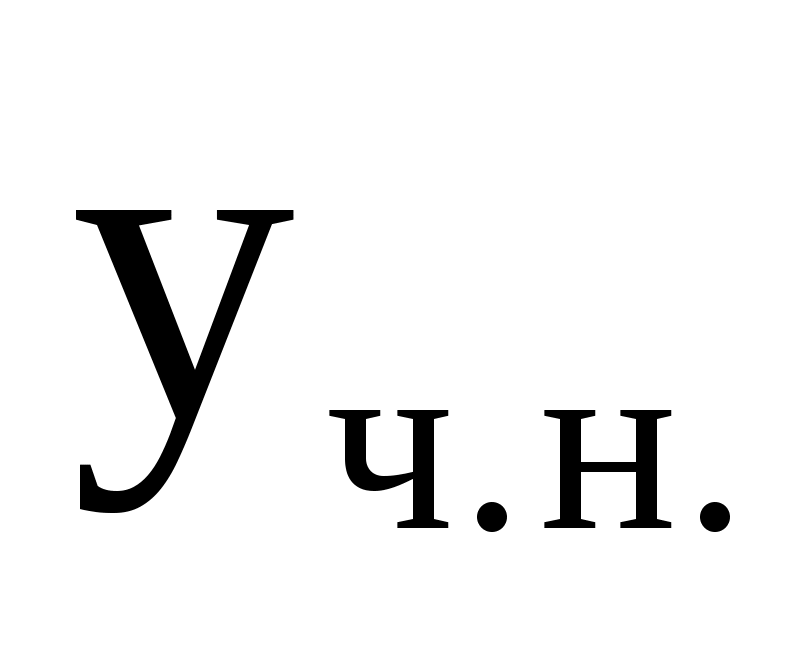 уравнения (1) находится в виде уравнения (1) находится в виде
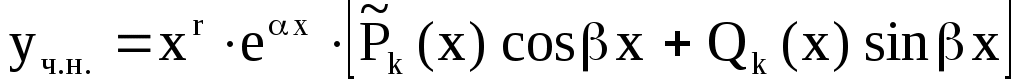 (3), (3),
где 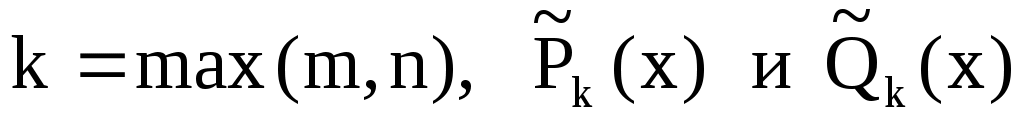 – многочлены от – многочлены от 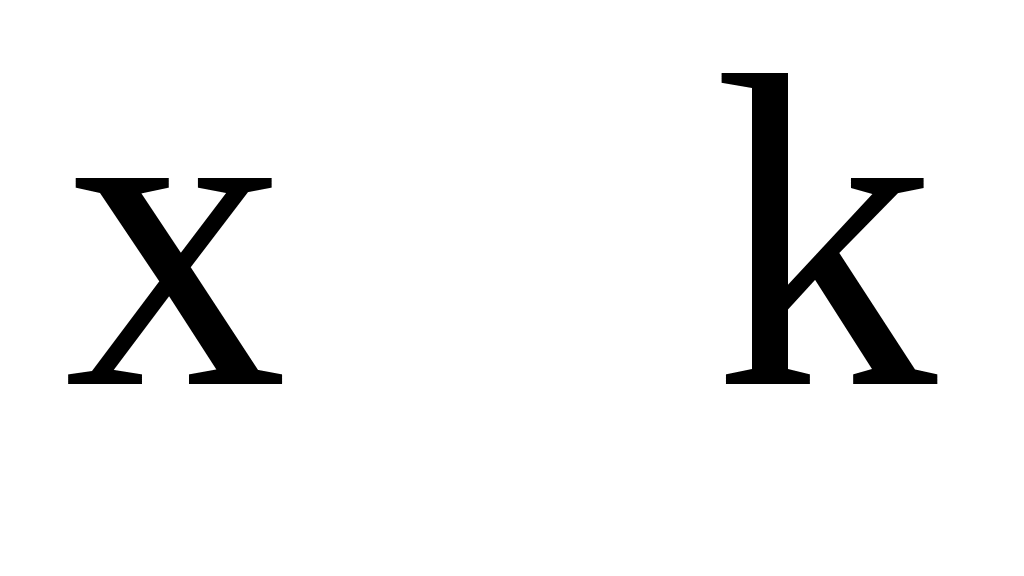 –й степени общего вида с неопределенными коэффициентами, а –й степени общего вида с неопределенными коэффициентами, а 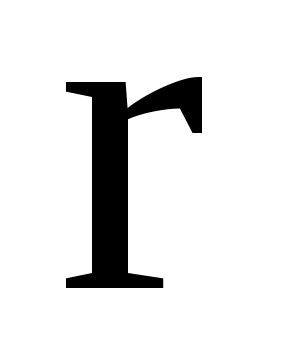 – кратность корня – кратность корня 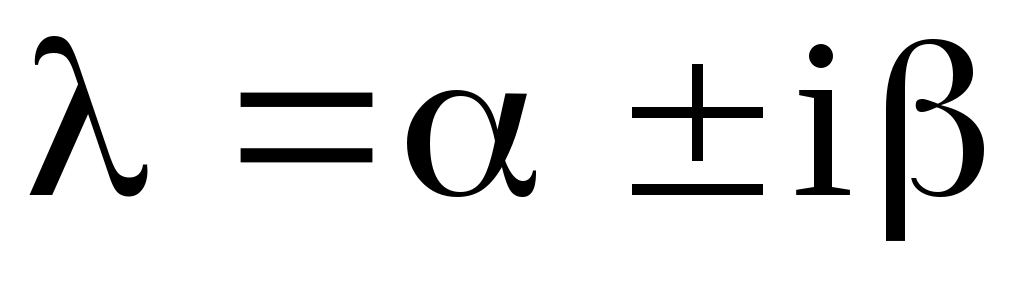 характеристического уравнения (если характеристического уравнения (если 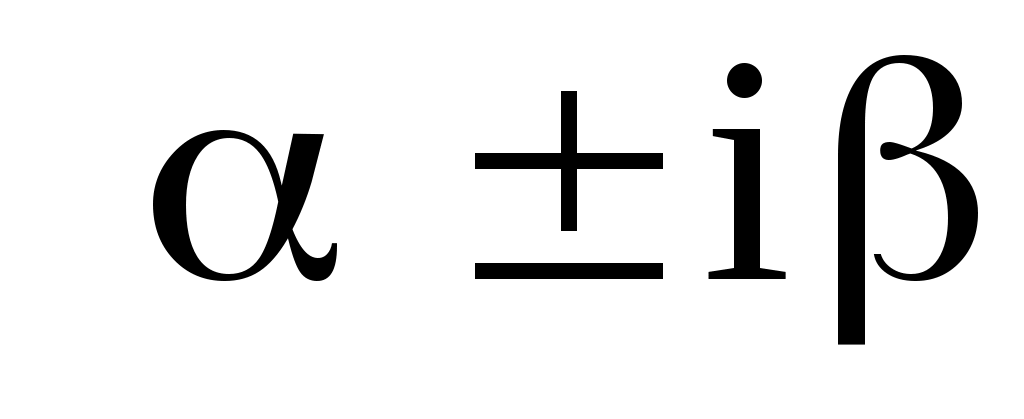 не является корнем характеристического уравнения, то не является корнем характеристического уравнения, то 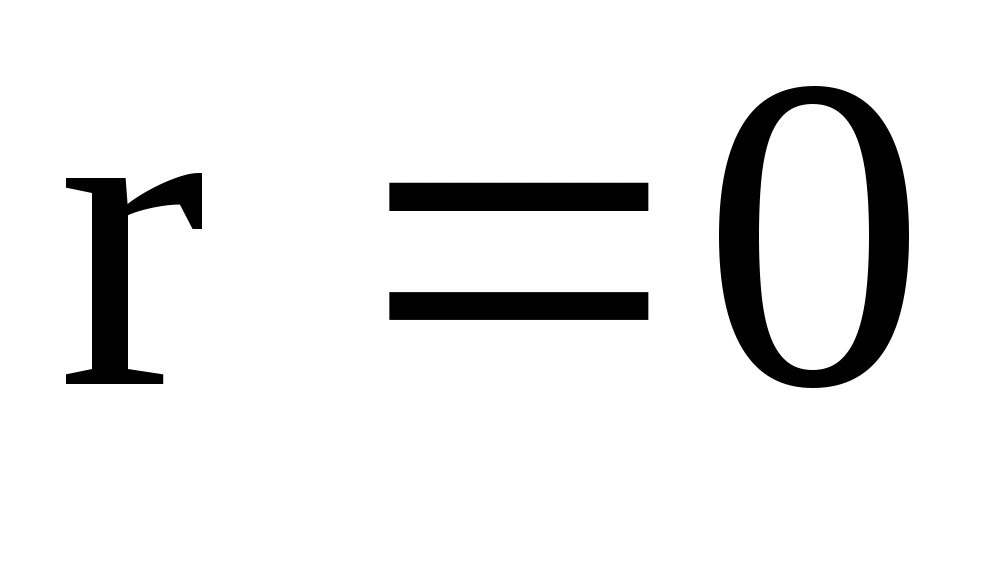 ). ).
Частные случаи 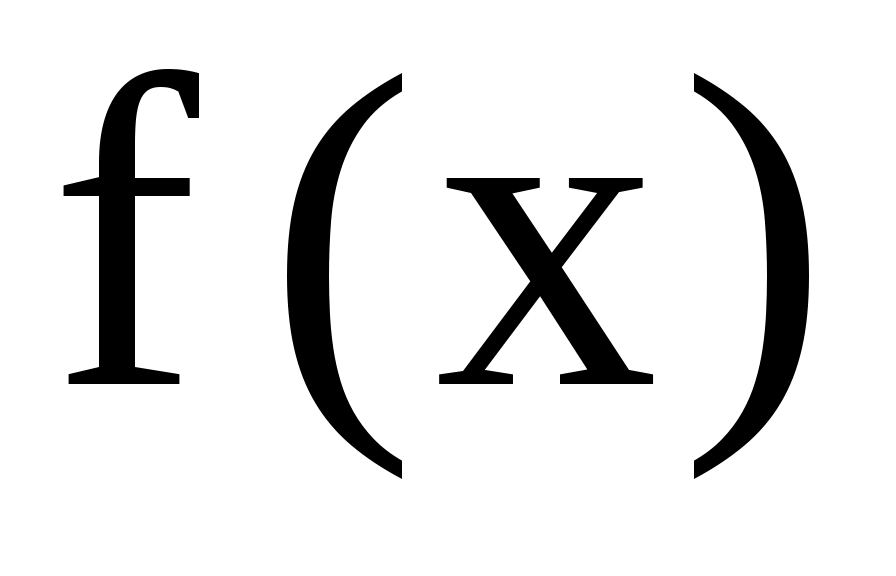 , определяемые формулой (2): , определяемые формулой (2):
I. 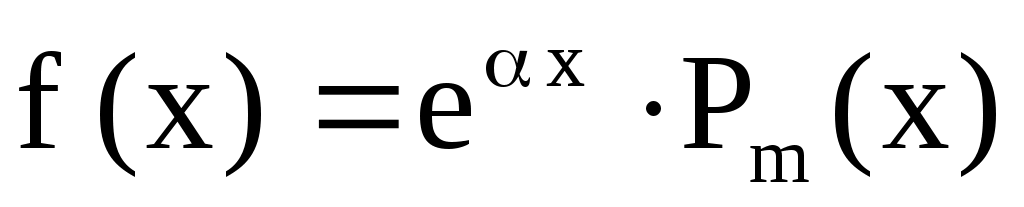 . .
1) если число 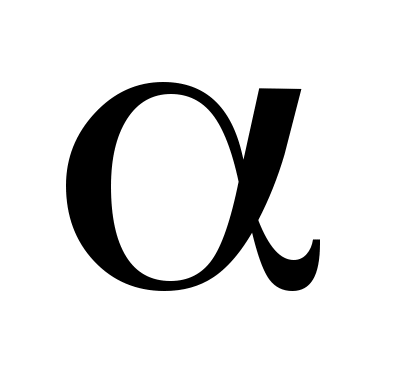 не является корнем х.у., то не является корнем х.у., то
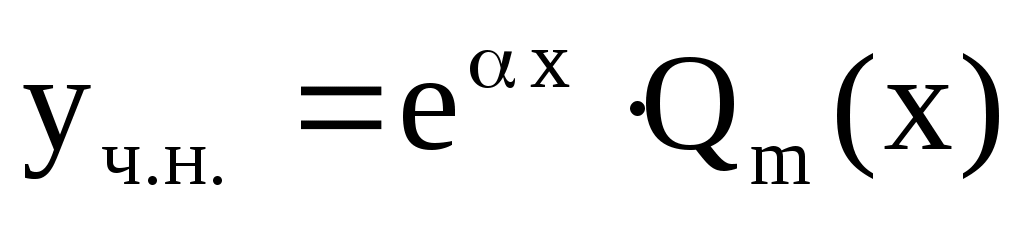 , ,
где 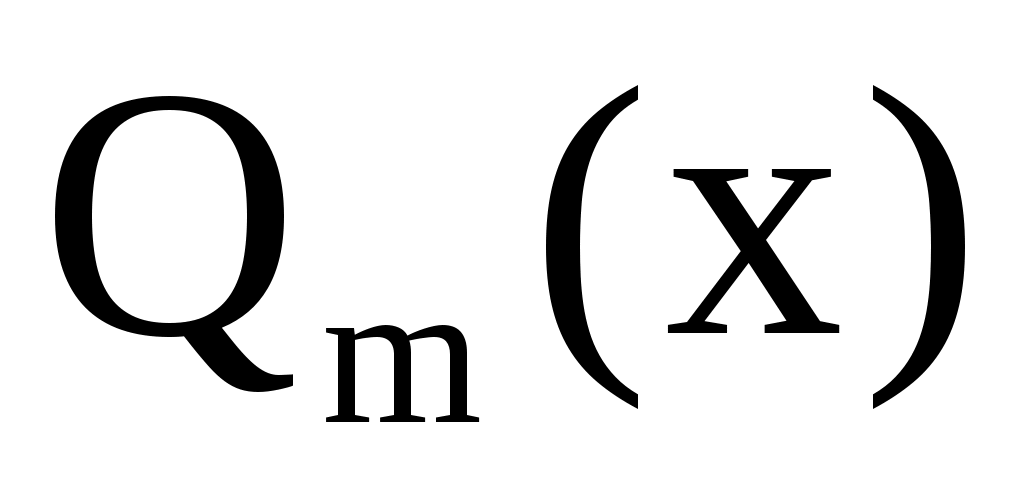 – многочлен той же степени, что и – многочлен той же степени, что и 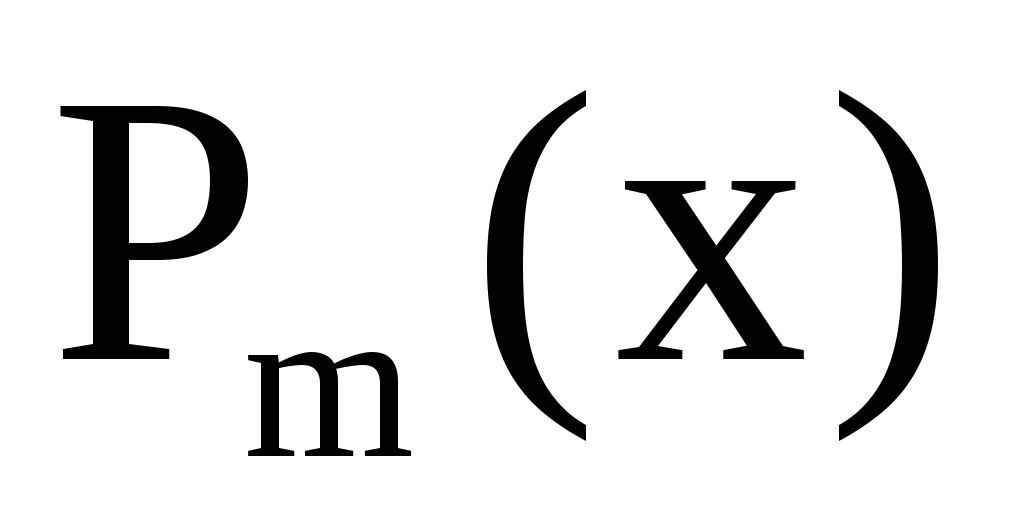 , но с неопределенными коэффициентами. , но с неопределенными коэффициентами.
2) число 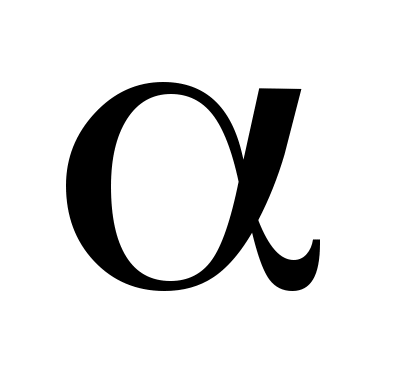 является корнем является корнем 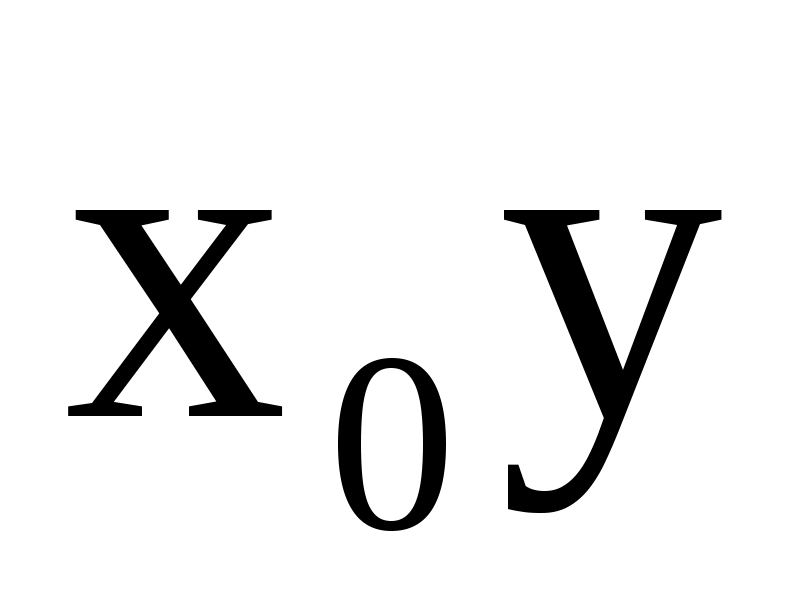 кратности кратности 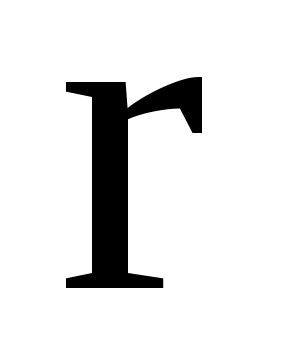 , то , то
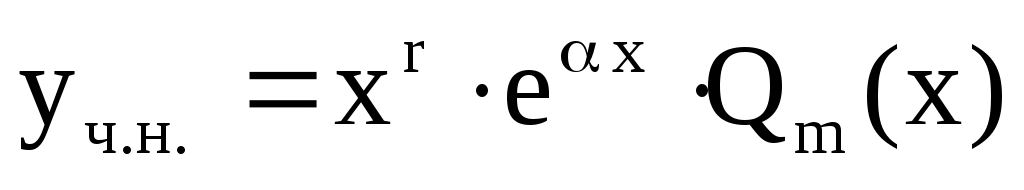 . .
II. 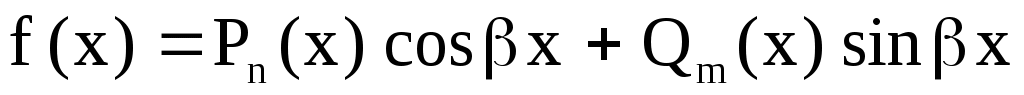 , то , то
если
1) 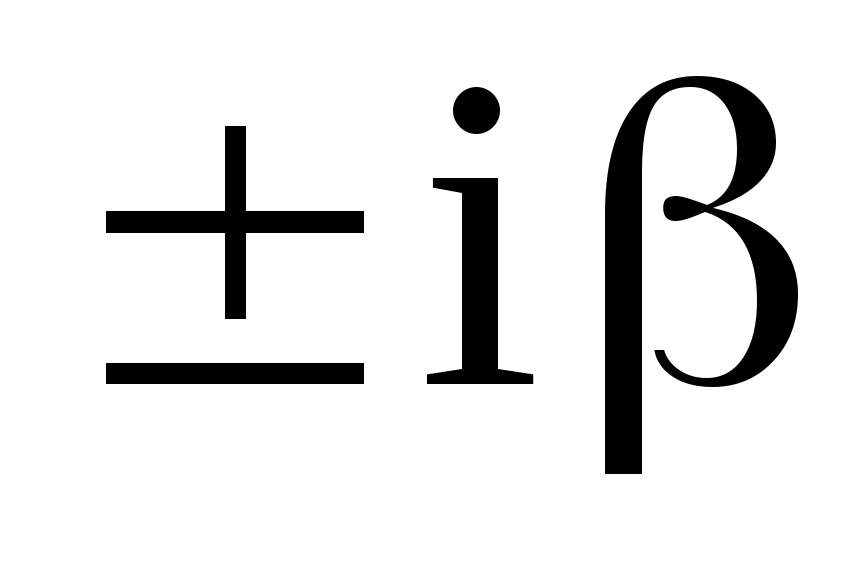 не является корнем х.у., то не является корнем х.у., то
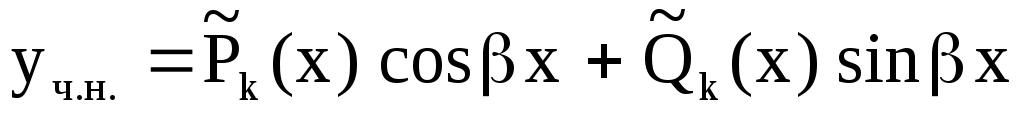 , , 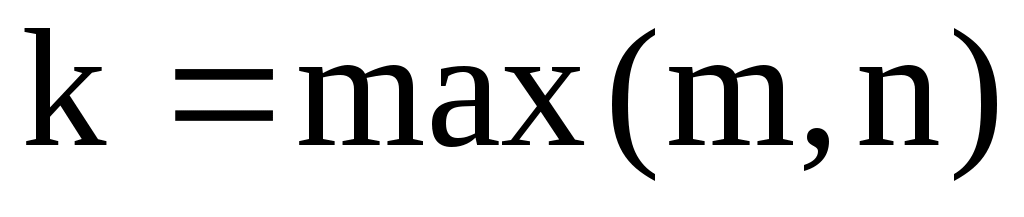 . .
2) число 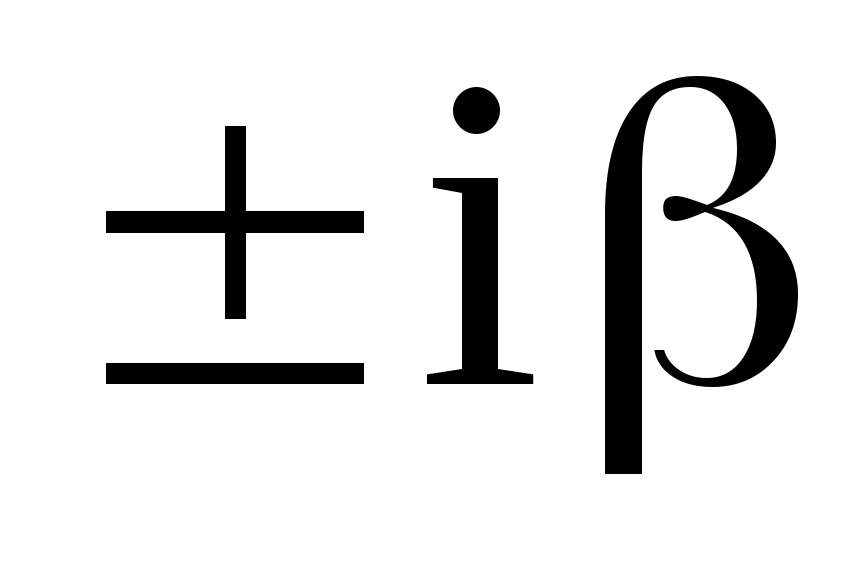 является корнем х.у. кратности является корнем х.у. кратности 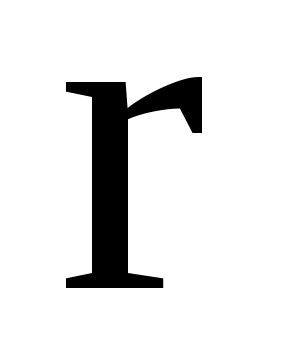 , то , то
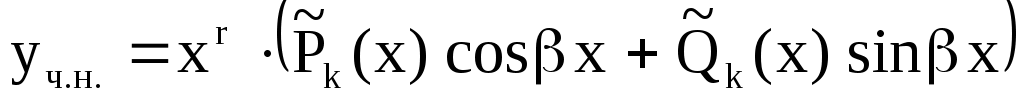 . .
III. 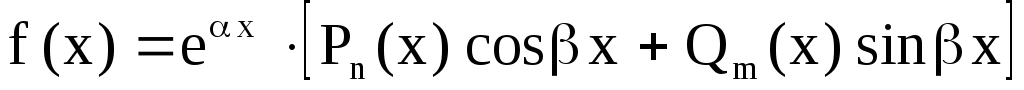 , то , то
если
1) число 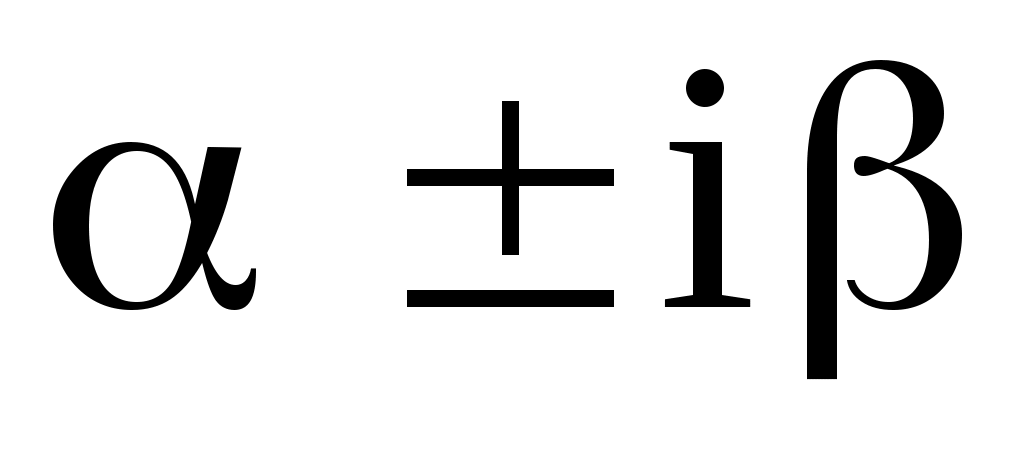 не является корнем х.у., то не является корнем х.у., то
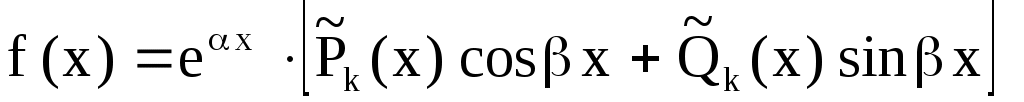 . .
2) число 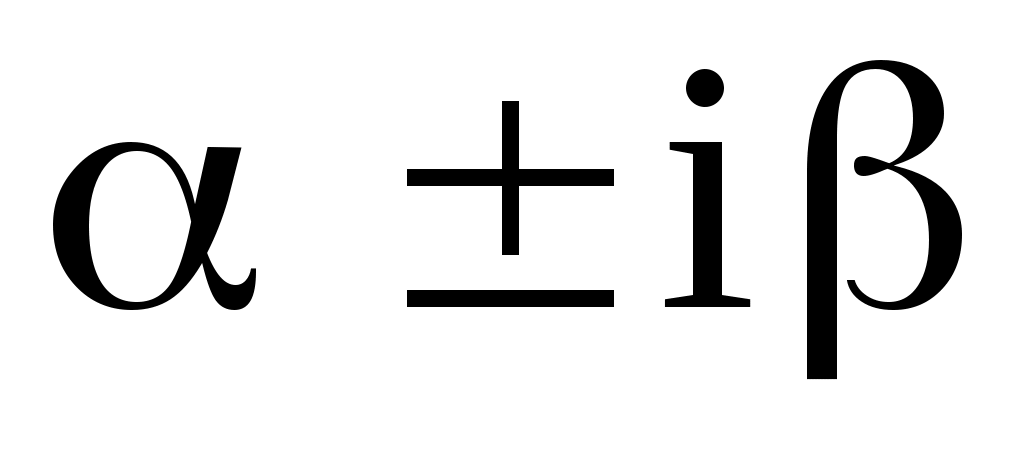 является корнем х.у. кратности является корнем х.у. кратности 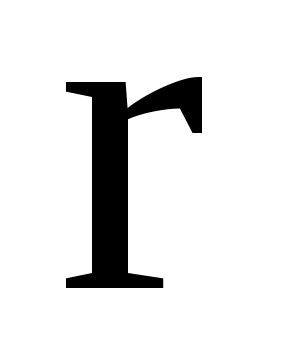 , то , то
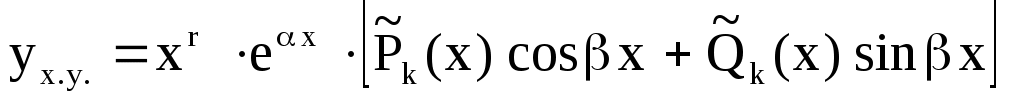 . .
Замечание. Первые два вида являются частными случаями III вида.
Пример 16. Найти общее решение уравнения 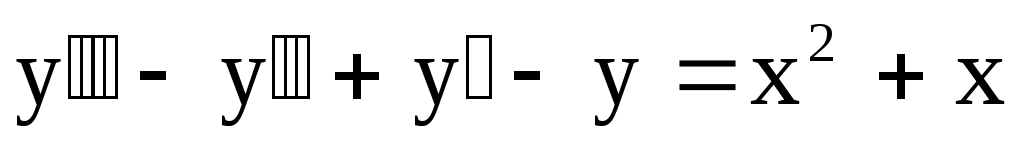 . .
Решение.
Характеристической уравнение (х.у.) 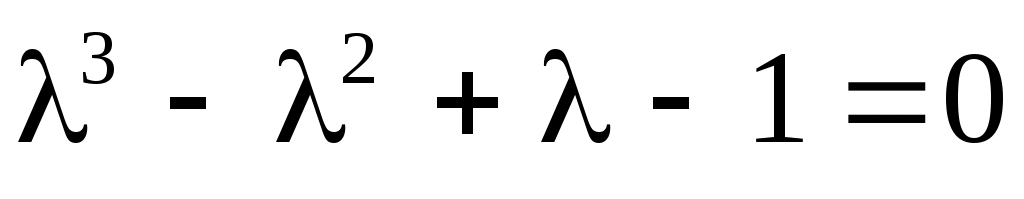 имеет различные корни имеет различные корни 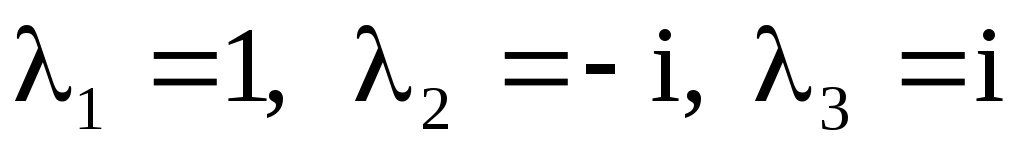 , поэтому общее решение , поэтому общее решение
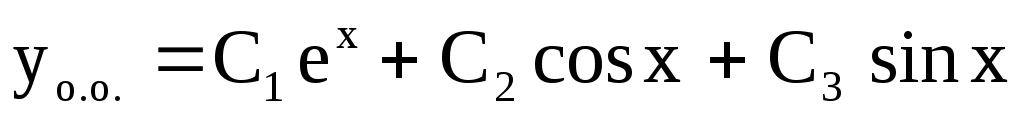 . .
Находим частное решение 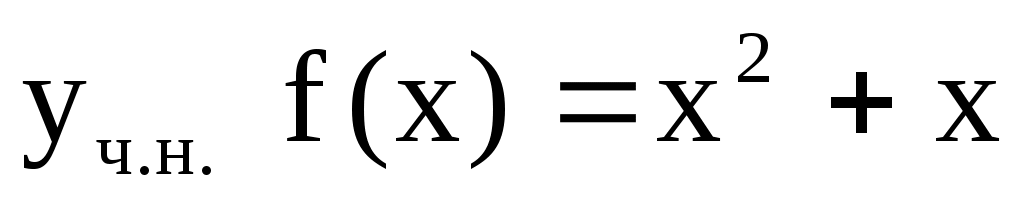 ; это многочлен ; это многочлен 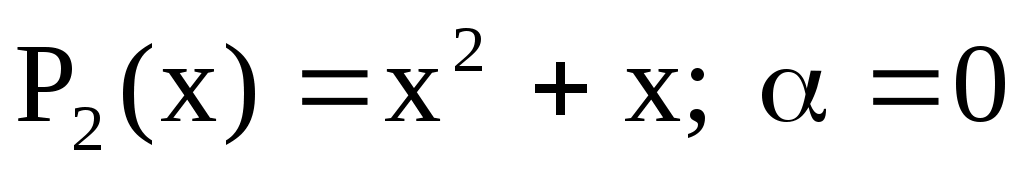 – не является корнем х.у., поэтому – не является корнем х.у., поэтому
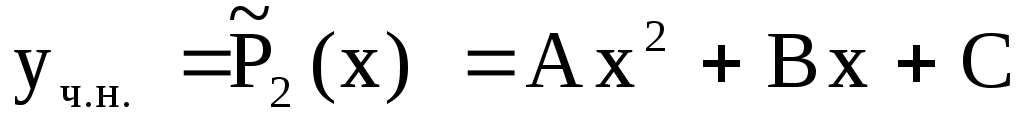 , ,
А, В, С – неопределенные (неизвестные) коэффициенты.
Подставляя 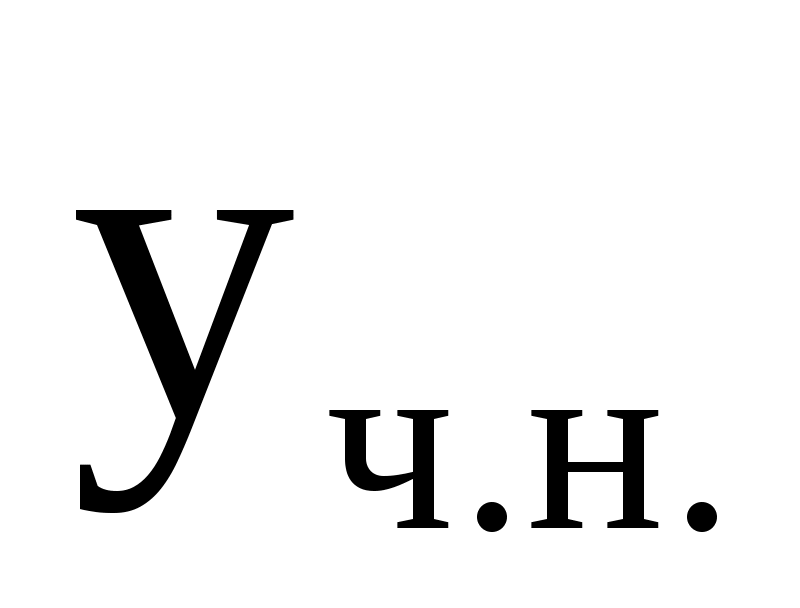 в уравнение, получим в уравнение, получим
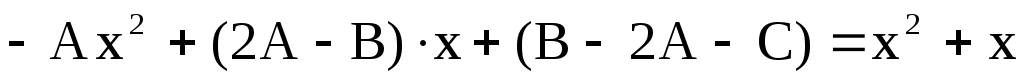 . .
Откуда
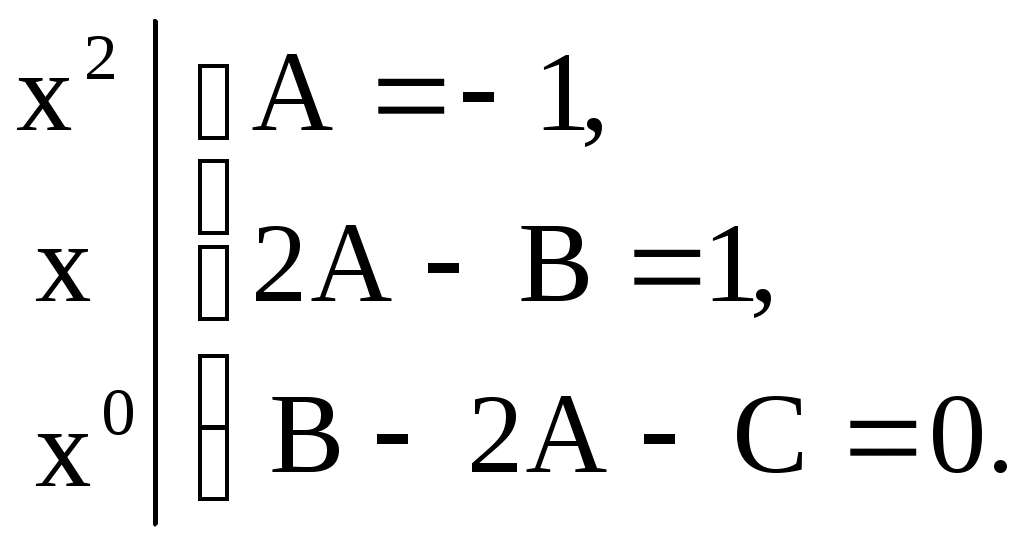
Решая систему, находим 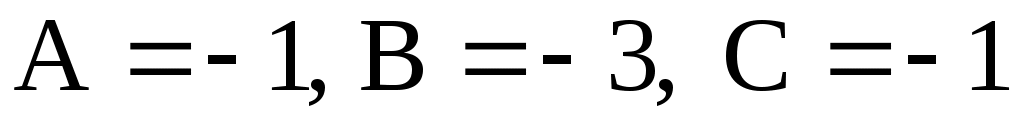 . Следовательно, . Следовательно, 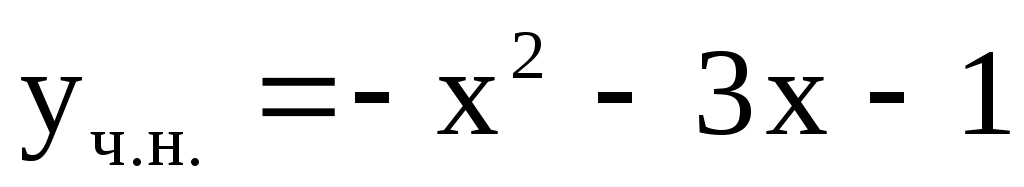 и общее решение будет и общее решение будет
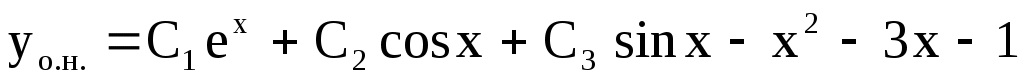 . .
Пример 17. Решить уравнение 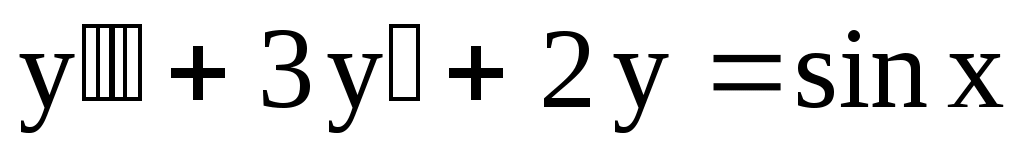 . .
Решение.
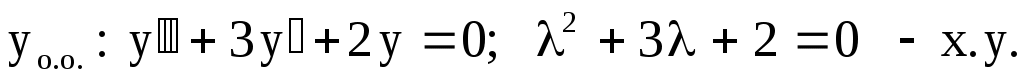
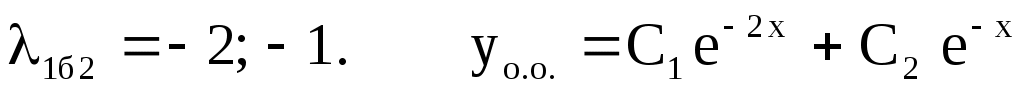 . .
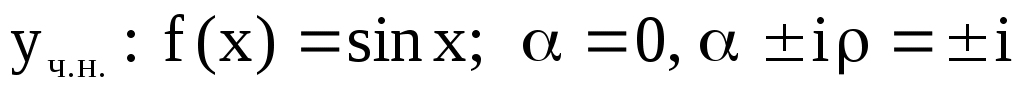 – нее является корнем х.у., поэтому – нее является корнем х.у., поэтому
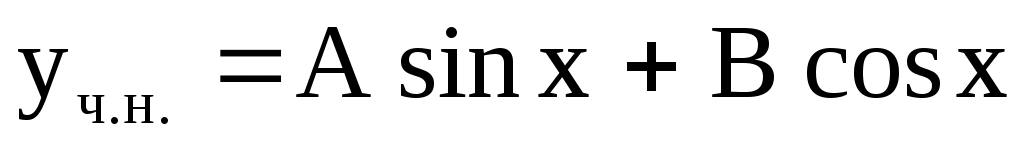 . .
Подставляя 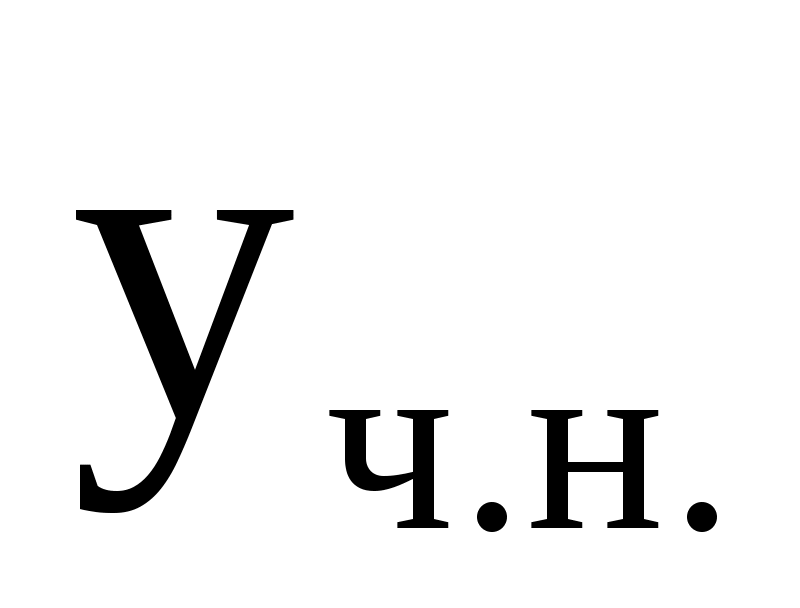 в уравнение в уравнение
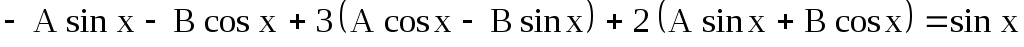 . .
Приравнивая коэффициенты при 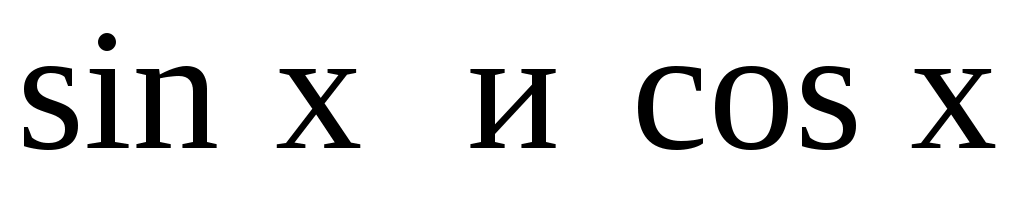 слева и справа, получим систему уравнений относительно неизвестных А и В. слева и справа, получим систему уравнений относительно неизвестных А и В.
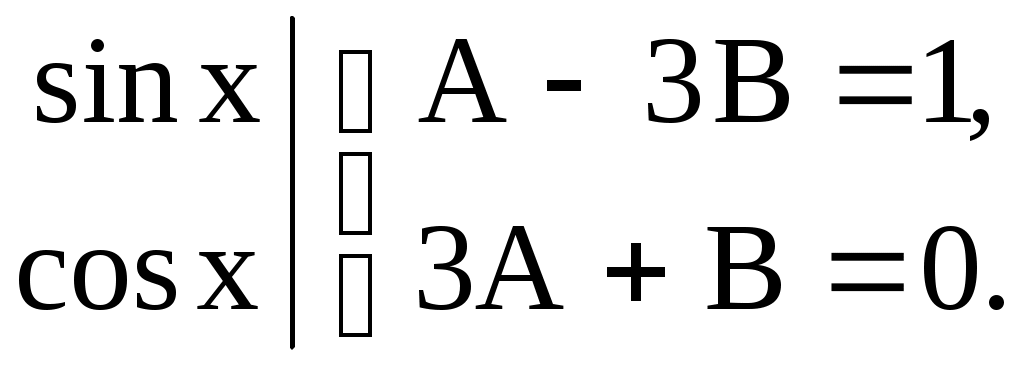 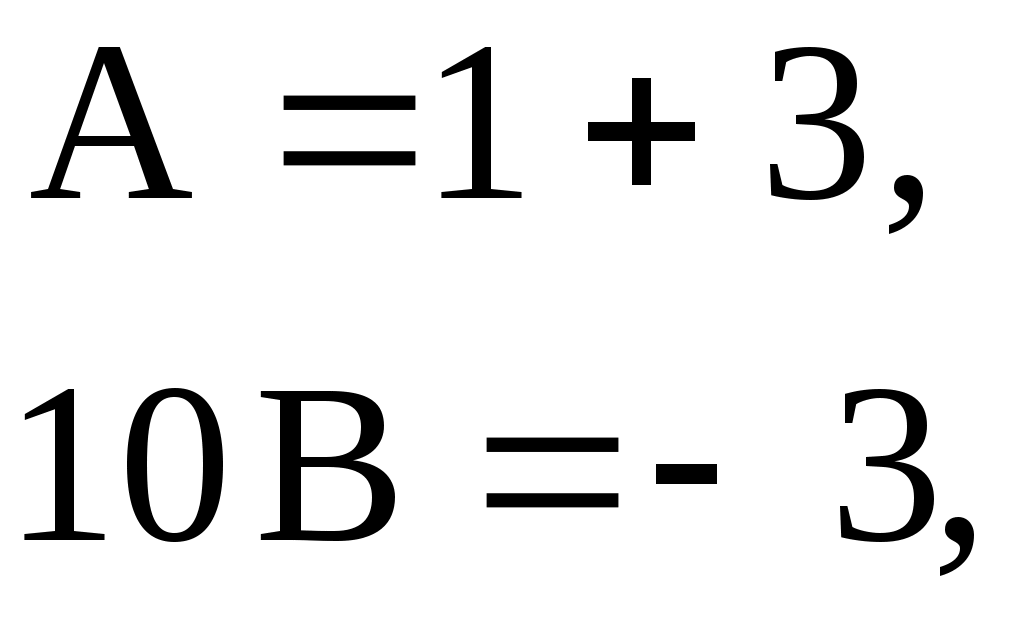 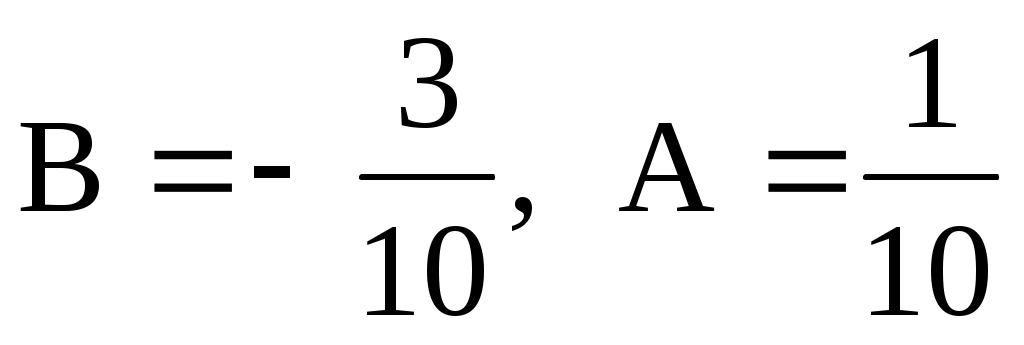 . .
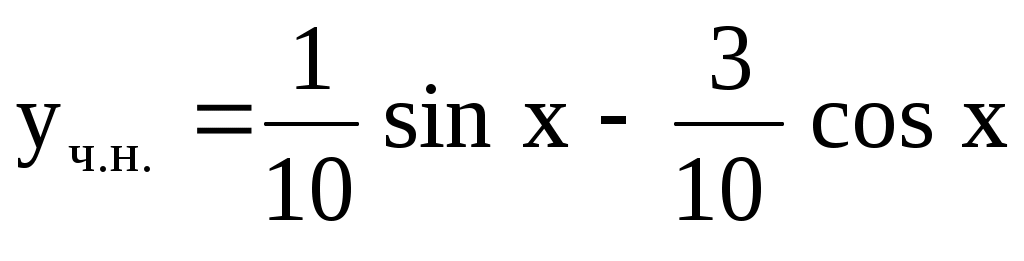 . .
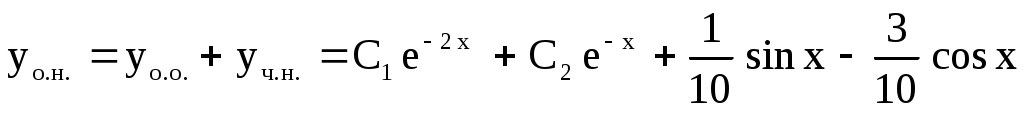 . .
Замечание. Если правая часть уравнения 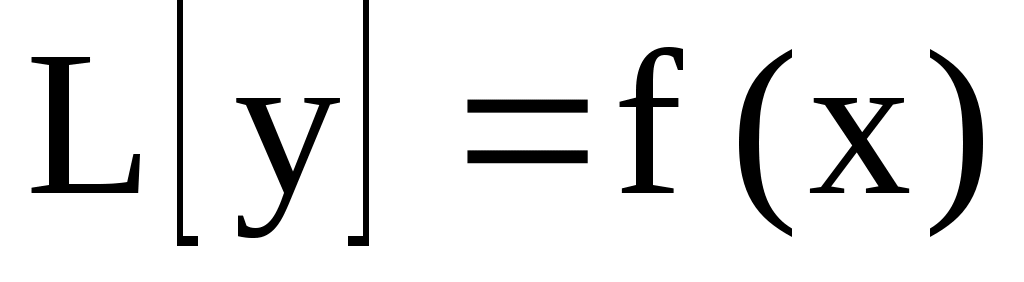 (1) имеет вид: (1) имеет вид: 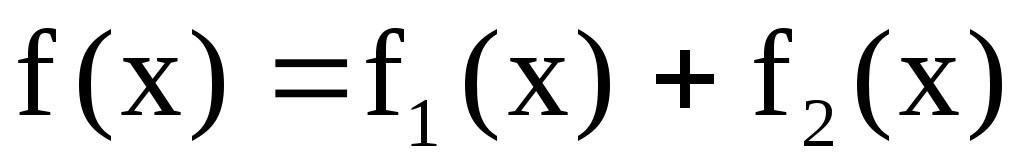 , то частное решение уравнения (1) , то частное решение уравнения (1) 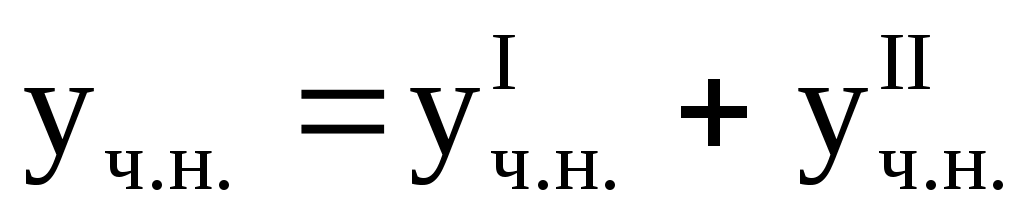 , где , где 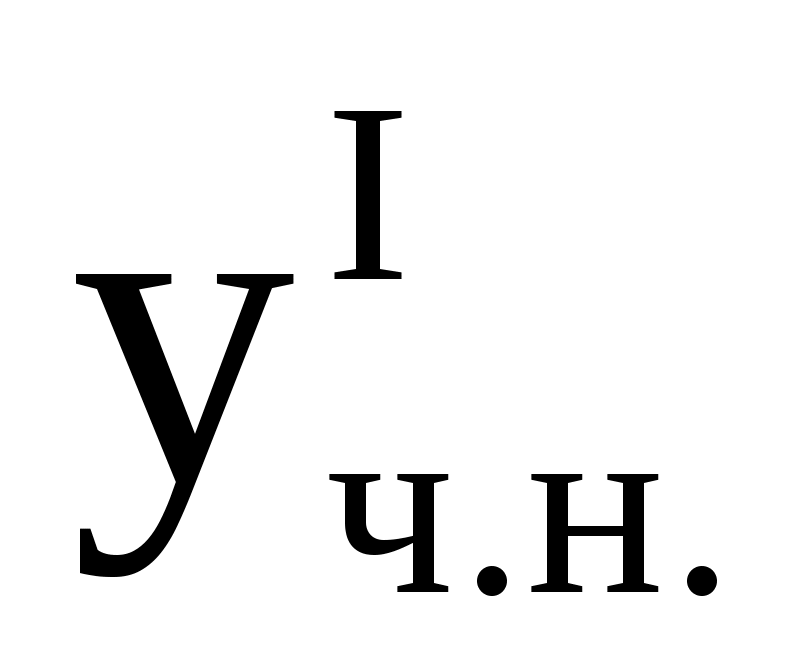 – частное решение уравнения – частное решение уравнения 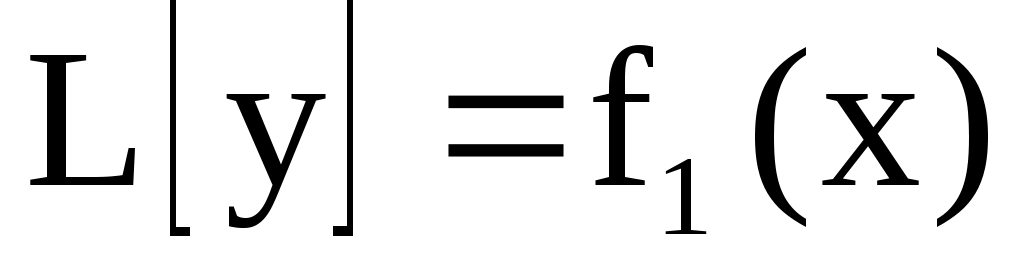 ; ; 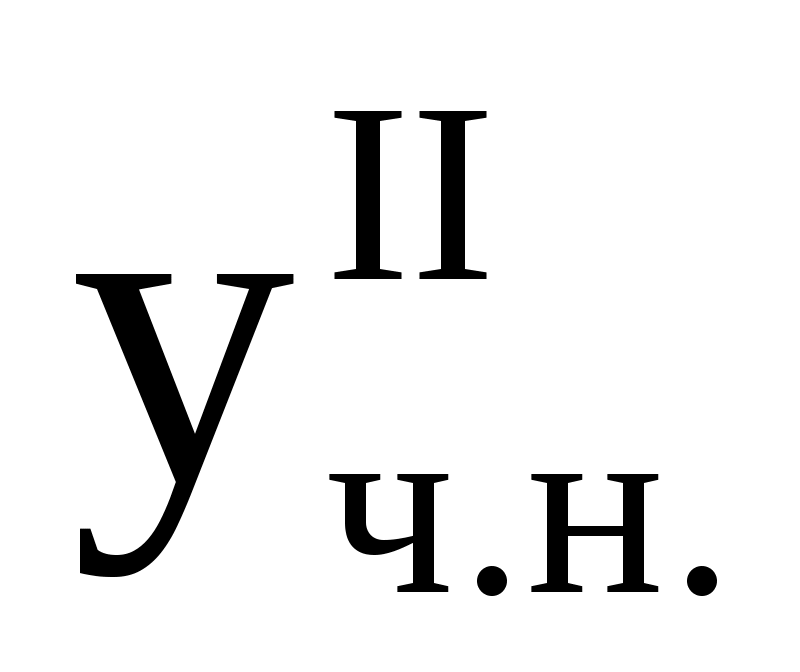 – частное решение уравнения – частное решение уравнения 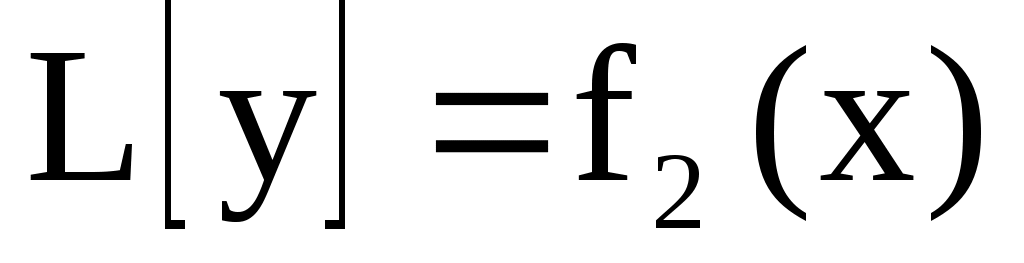 . .
Упражнения. Определить вид частного решения.
1) 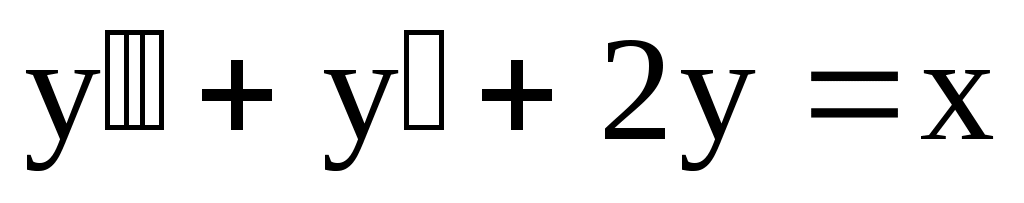 . Ответ: . Ответ: 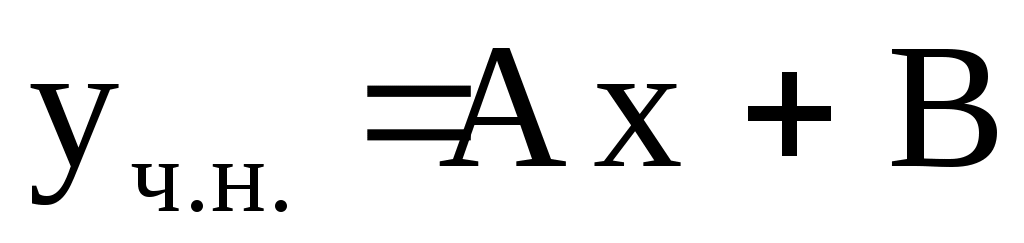 . .
2) 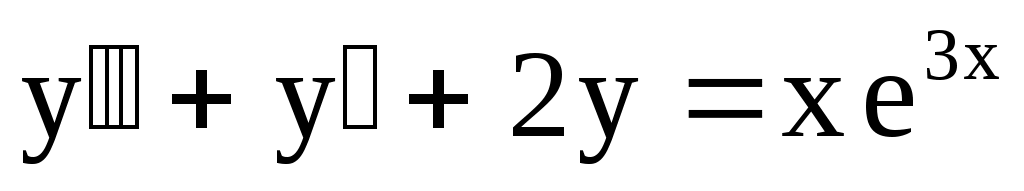 . Ответ: . Ответ: 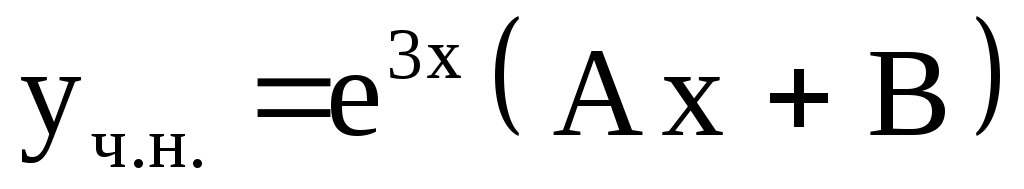 . .
3)  . Ответ: . Ответ: 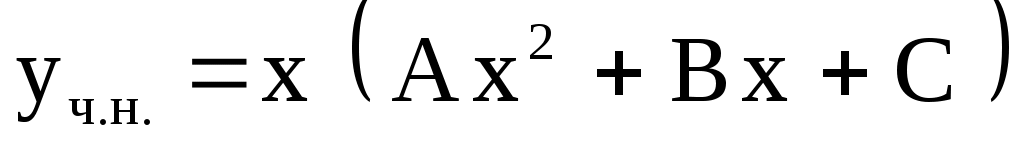 . .
4) 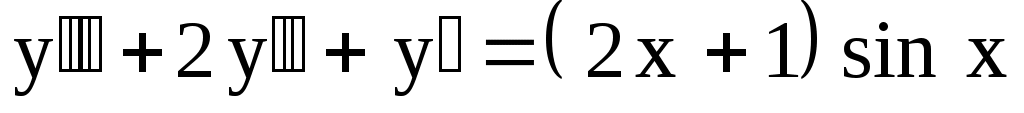 . Ответ: . Ответ: 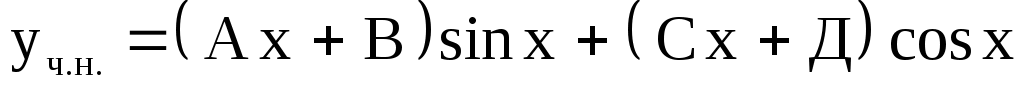 . .
Контрольное задание № 10.
Для следующих линейных неоднородных дифференциальных уравнений определить вид частного решения не находя числовых значений коэффициентов:
-
1.
|
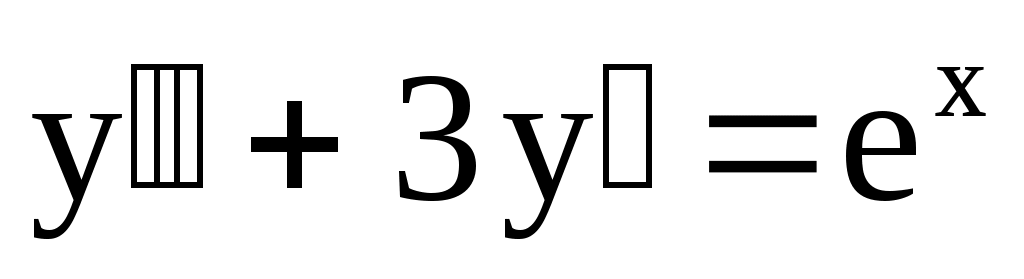 . .
|
2.
|
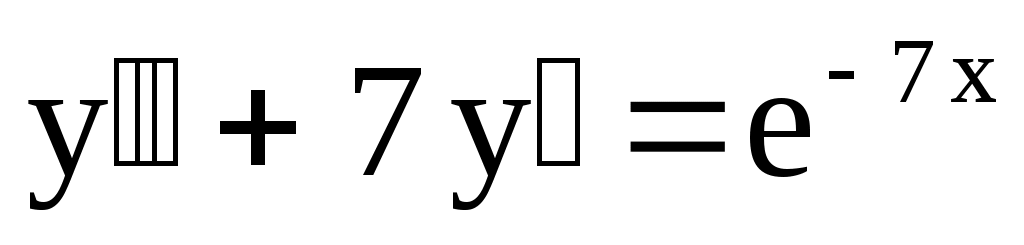 . .
|
3.
|
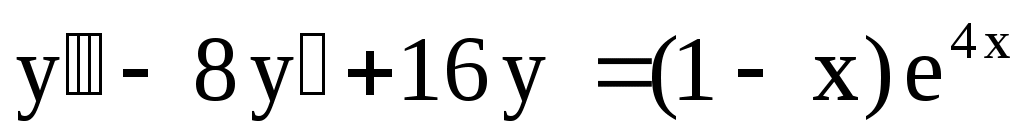 . .
|
4.
|
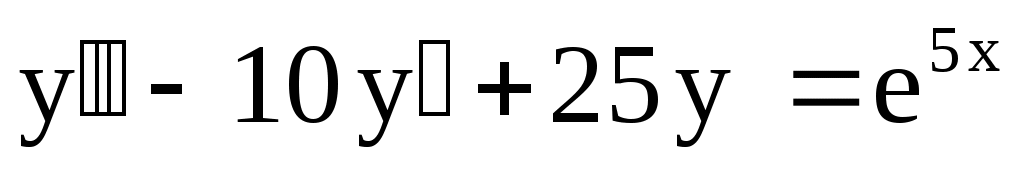 . .
|
5.
|
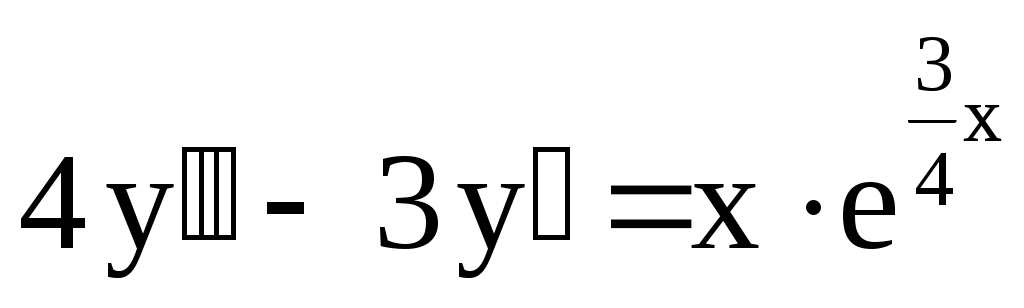 . .
|
6.
|
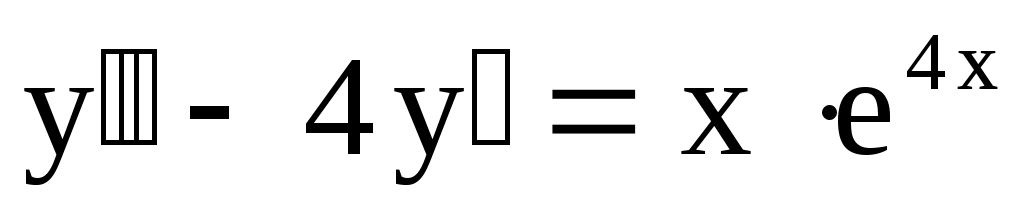 . .
|
7.
|
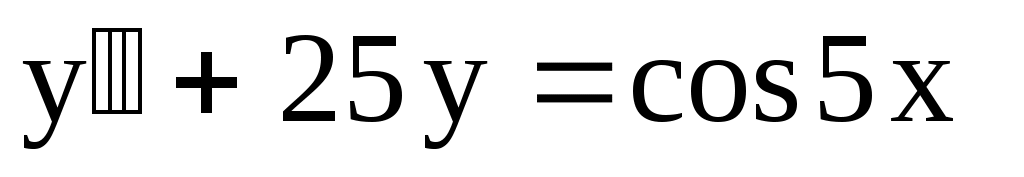 . .
|
8.
|
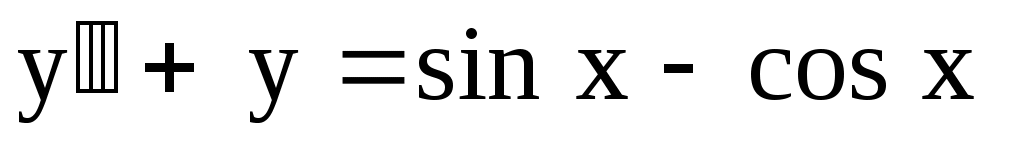 . .
|
9.
|
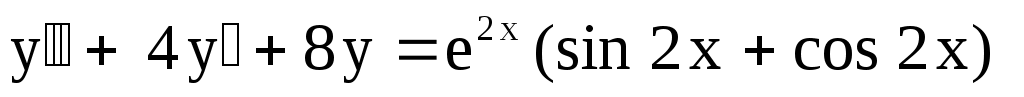 . .
|
10.
|
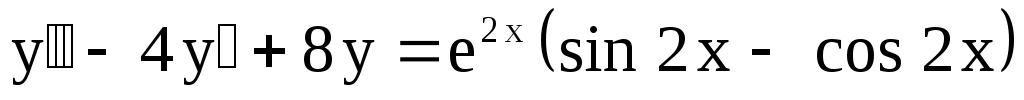 . .
|
11.
|
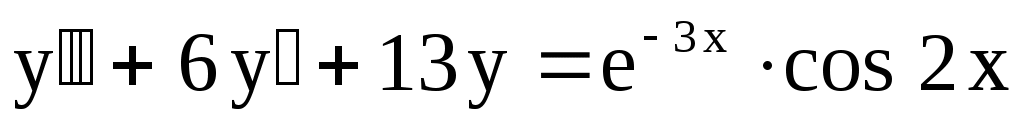 . .
|
12.
|
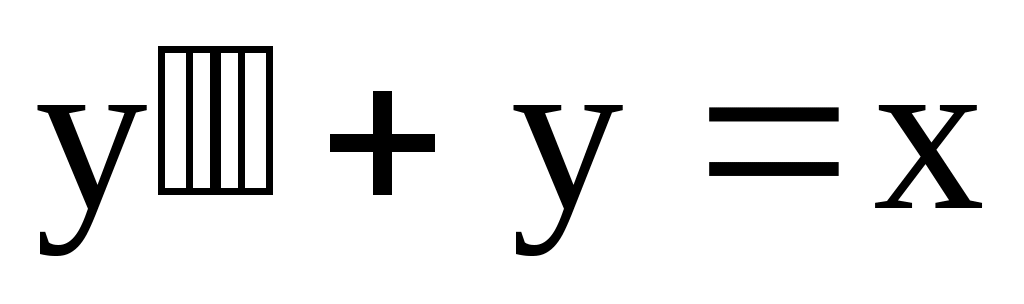 . .
|
13.
|
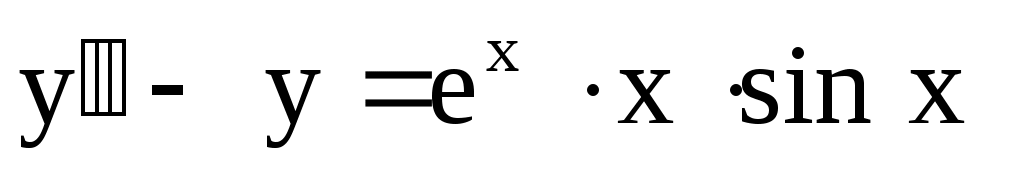 . .
|
14.
|
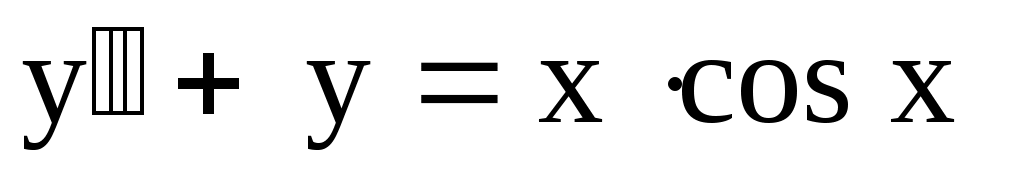 . .
|
15.
|
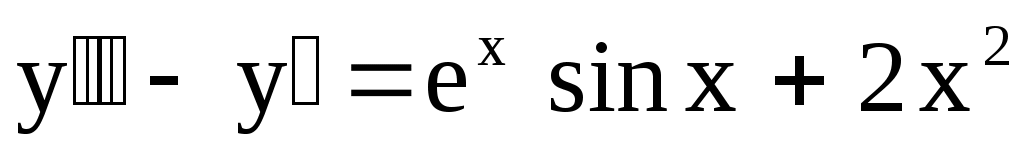 . .
|
16.
|
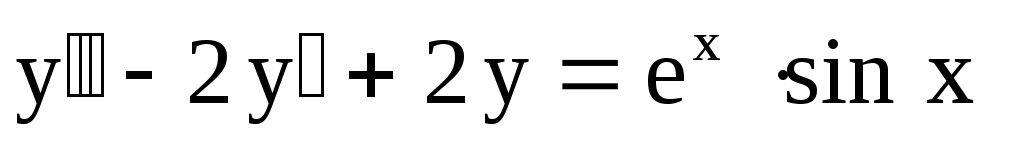 . .
|
17.
|
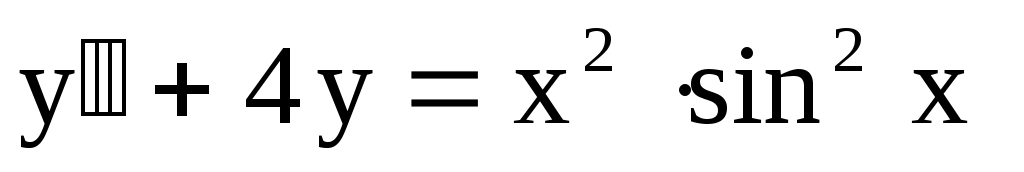 . .
|
18.
|
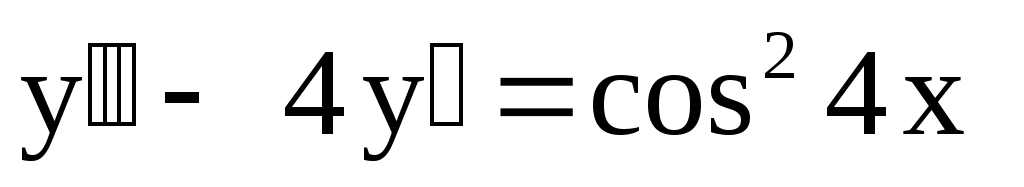 . .
|
19.
|
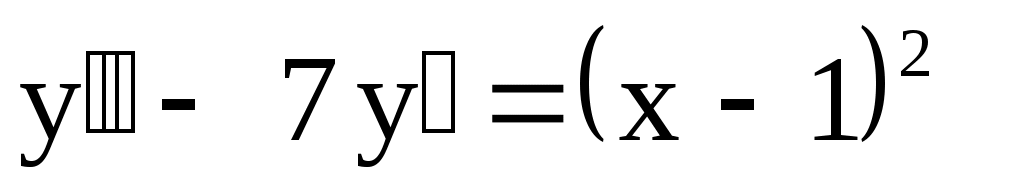 . .
|
20.
|
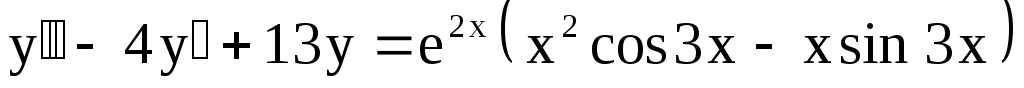 . .
|
21.
|
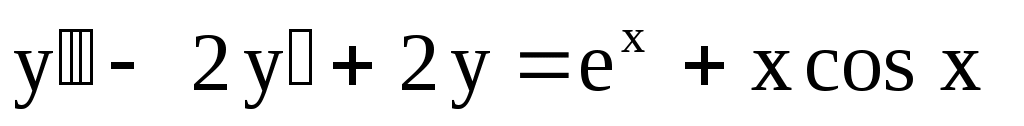 . .
|
22.
|
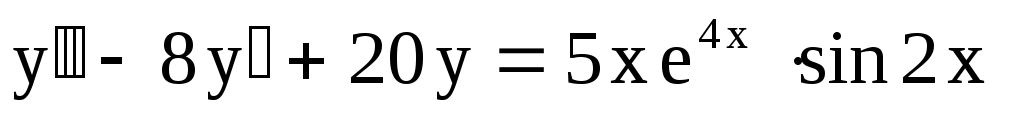 . .
|
23.
|
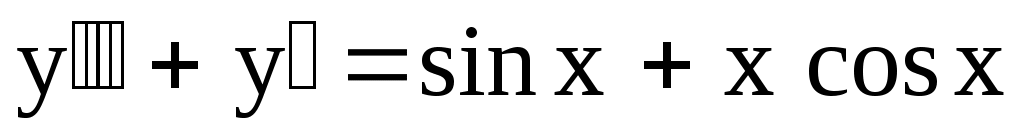 . .
|
24.
|
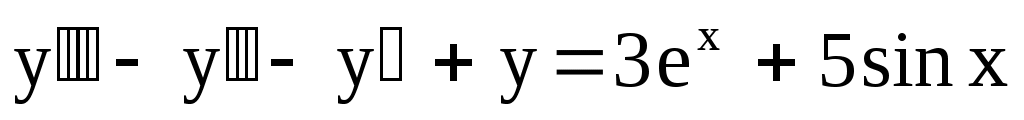 . .
|
25.
|
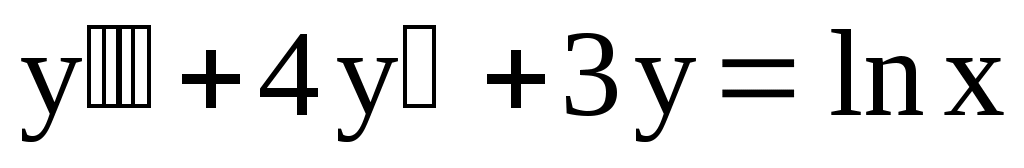 . .
|
26.
|
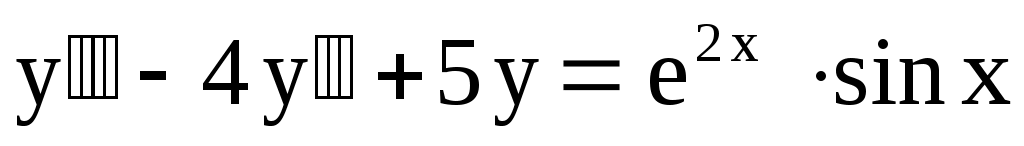 . .
|
27.
|
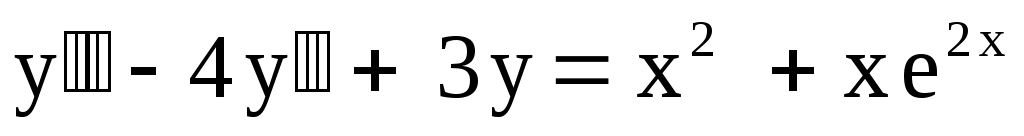 . .
|
28.
|
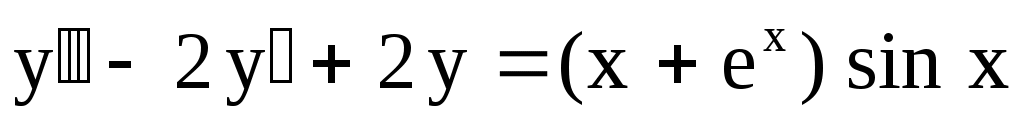 . .
|
29.
|
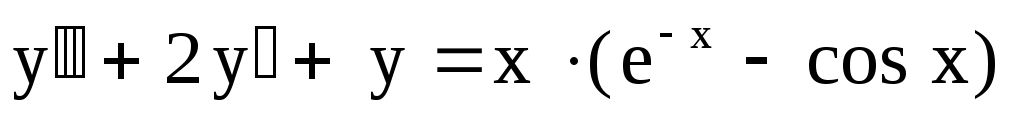 . .
|
30.
|
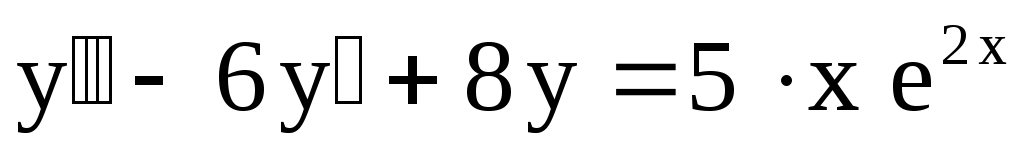 . .
|
Упражнения. Решить уравнения.
1) 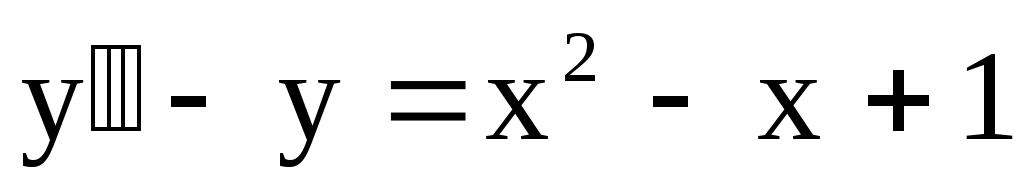 . Ответ: . Ответ: 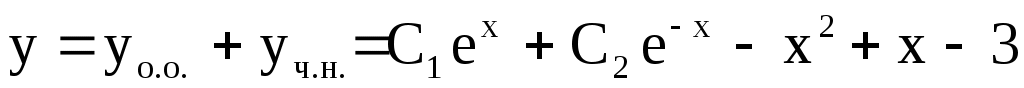 . .
2) 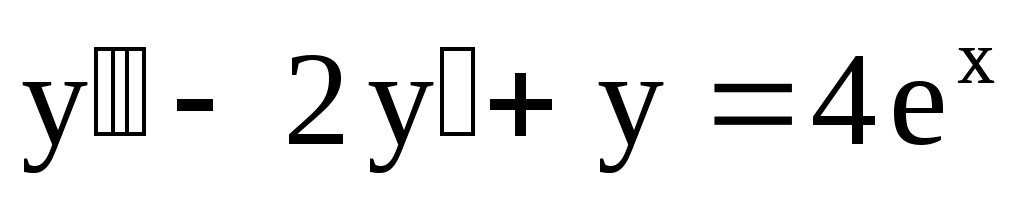 . Ответ: . Ответ: 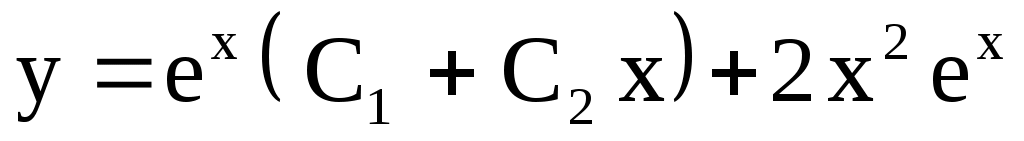 . .
3) 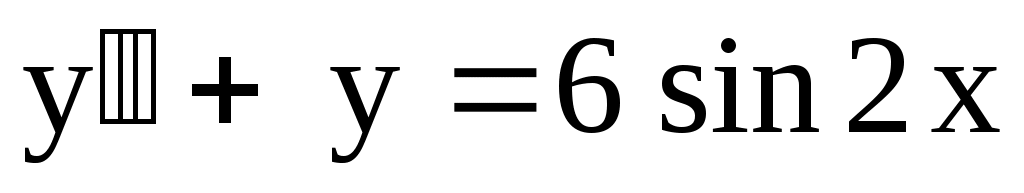 . Ответ: . Ответ: 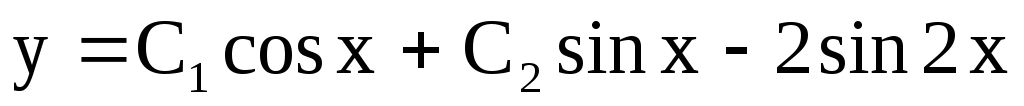 . .
4) 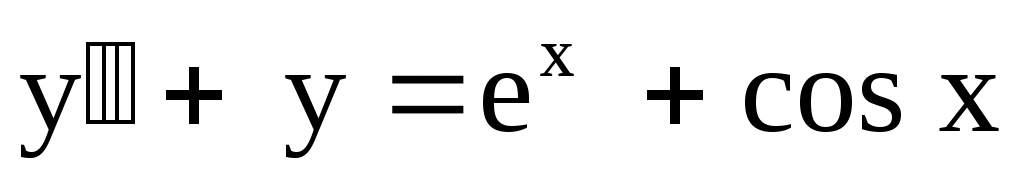 . Ответ: . Ответ: 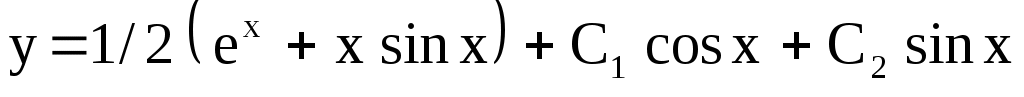 . .
Замечание. Следует найти отдельно два частных решения 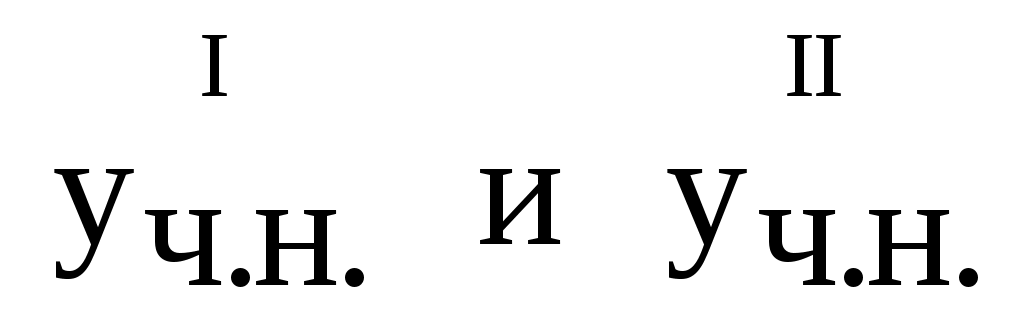 соответствующие соответствующие 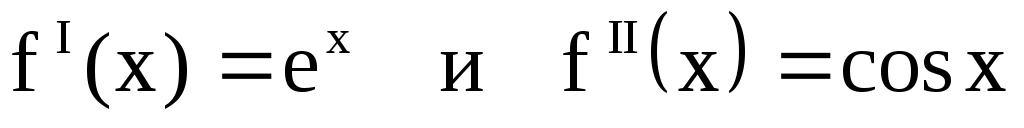 , но можно найти их и вместе. , но можно найти их и вместе.
|
|
|
 Скачать 1.81 Mb.
Скачать 1.81 Mb.