высшая математика. 10 Обыкновенные диф-ые ур-ия. Контрольная работа. Контрольная работа 10 Обыкновенные дифференциальные уравнения. Задачи 112
 Скачать 1.81 Mb.
|
|
Контрольное задание № 11. Решить следующие линейные неоднородные уравнения с правой частью специального вида методом подбора частного решения по виду правой части.
Задача 12. Метод вариации произвольных постоянных, метод Лагранжа. Рассмотрим метод вариации произвольных постоянных для уравнения второго порядка  (1)Если известна фундаментальная система решений соответствующего однородного уравнения  , (2),то общее решение неоднородного уравнения (1) может быть найдено методом вариации постоянных (метод Лагранжа). Общее решение уравнения (2) имеет вид  , (3)где  – фундаментальная система решений (ф.с.р.), – произвольные постоянные.Решение уравнения (1) будем находить в виде 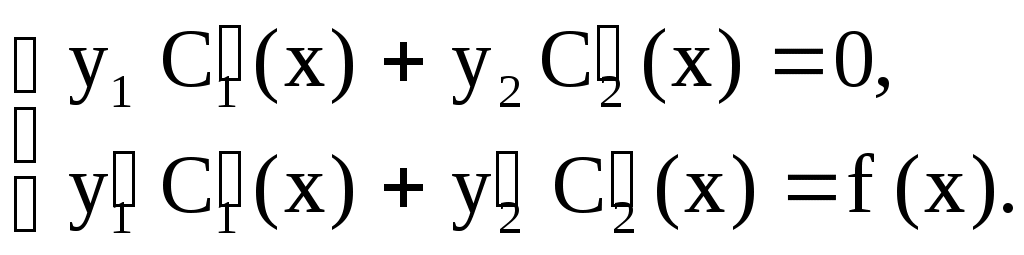 , (4)где  – некоторые пока неизвестные функции от х. Для их определения получаем систему (5)Решая (5) относительно  , получим (6) – определитель Вронского. , т. к. – ф. с. р.Из (6) находим  ,где  – постоянные интегрирования.Пример 18. Решить уравнение  .Решение. Соответствующее однородное уравнение будет  .Его характеристическое уравнение  и общее решение имеет вид  .Общее решение исходного уравнения имеем в виде  (*) – ф. с. р. – неизвестные функции от  . Для их нахождения составим систему  Решаем эту систему относительно  : .Интегрируя, находим  .Подставляя выражения  в (*), получаем общее решение искомого уравнения .Здесь  – частное решение исходного уравнения.Упражнения. Решить уравнения. 1)  . Ответ:  .2)  . Ответ:  .3)  . Ответ:  .4)  . Ответ:  ,или  .Контрольное задание № 12. Решить методом вариации произвольных постоянных следующие уравнения:
|
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.