высшая математика. 10 Обыкновенные диф-ые ур-ия. Контрольная работа. Контрольная работа 10 Обыкновенные дифференциальные уравнения. Задачи 112

• Название: Контрольная работа 10 Обыкновенные дифференциальные уравнения. Задачи 112
• Анкор: высшая математика
• Дата: 25.12.2022
• Размер: 1.81 Mb.
• Имя файла: 10 Обыкновенные диф-ые ур-ия. Контрольная работа.doc
• Тип: Контрольная работа; #863700
• страница: 2 из 7

Контрольное задание № 2.

Решить однородные дифференциальные уравнения.

1.	.
2.	.
3.	.
4.	.
5.	.
6.	.
7.	.
8.	.
9.	.
10.	.
11.	.
12.	.
13.	.
14.	.
15.	.
16.	.
17.	.
18.	.
19.	.
20.	.
21.	.
22.	.
23.	.
24.	.
25.	.
26.	.
27.	.
28.	.
29.	.
30.	.

Задача 3. Линейные дифференциальные уравнения первого порядка.

Линейным дифференциальным уравнением первого порядка называется уравнение линейное относительно неизвестной функции и ее производной. Оно имеет вид

(1)

где - заданные функции от , непрерывные в той области, в которой требуется проинтегрировать уравнение (1).

Если , то уравнение (1) называется линейным однородным. Оно является уравнением с разделяющимися переменным и имеет общее решение

.

Общее решение неоднородного уравнения можно найти следующими способами:

1) методом вариации произвольной постоянной, который состоит в том, что

решение уравнения (1) находится в виде

, где - новая неизвестная функция.

2) уравнение (1) может быть проинтегрирован с помощью подстановки , где - неизвестные функции от .

3) решение уравнения (1) можно найти еще и по формуле

.

Замечание. Может оказаться, что дифференциальное уравнение линейно относительно как функции от . Нормальный вид (коэффициент при равен 1) такого уравнения

( )

Пример 4.

Решить уравнение .

Решение. Вид уравнения нормальный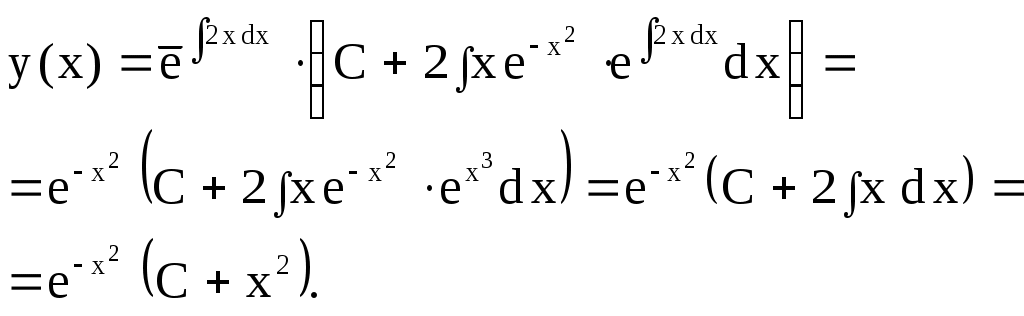

.



Ответ: .
Упражнения. Решить уравнения

1. . Ответ: .

2. .

Приводим к виду , и решаем по формуле . Ответ: .

3. . Ответ: .

4. . Ответ: .
Уравнение линейное относительно функции . Приводим его к виду

или .
Контрольное задание № 3.

Решить линейные дифференциальные уравнения первого порядка:

1.	.
2.	.
3.	; .
4.	.
5.	.
6.	.
7.	.
8.	.
9.	.
10.	.
11.	.
12.	.
13.	.
14.	.
15.	.
16.	.
17.	.
18.	.
19.	.
20.	.
21.	.
22.	.
23.	.
24.	.
25.	.
26.	.
27.	.
28.	.
29.	.
30.	.

Задача 4. Уравнение Бернулли.

Уравнение Бернулли имеет вид

(1)

(при это уравнение является линейным).

Уравнение (1) умножим на

(2)

Обозначим .

Уравнение (2) умножим на

или

(3)

(3) – линейное уравнение относительно переменной .

Таким образом, уравнение Бернулли можно привести к линейному уравнению.

Замечание. Уравнение Бернулли может быть проинтегрировано также методом вариации постоянной, как линейное уравнение и с помощью подстановки .