Итоговая математика.. Размах вариации Размах вариации
 Скачать 35.05 Kb.
|
|
Размах вариации Размах вариации – разница между максимальным и минимальным значением:  Ниже приведена графическая интерпретация размаха вариации. 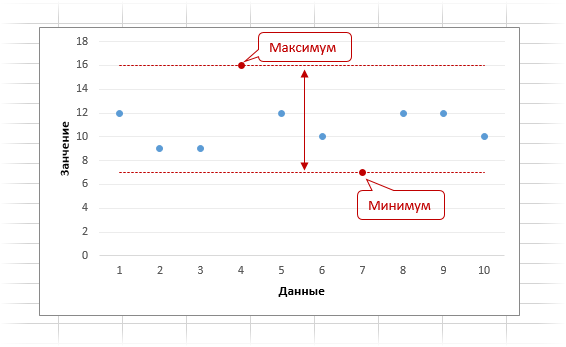 Видно максимальное и минимальное значение, а также расстояние между ними, которое и соответствует размаху вариации. С одной стороны, показатель размаха может быть вполне информативным и полезным. К примеру, максимальная и минимальная стоимость квартиры в городе N, максимальная и минимальная зарплата по профессии в регионе и проч. С другой стороны, размах может быть очень широким и не иметь практического смысла, т.к. зависит лишь от двух наблюдений. Таким образом, размах вариации очень неустойчивая величина. Коэффициент вариации определяется как отношение стандартного отклонения σ к среднему μ: cv ={\displaystyle {\frac {\sigma }{\mu }}}  [1]. Он показывает степень изменчивости по отношению к среднему показателю выборки. Коэффициент вариации следует вычислять только для данных, измеренных на шкале отношений, то есть шкал, которые имеют значимый нуль и, следовательно, допускают относительное сравнение двух измерений. Коэффициент вариации может не иметь никакого значения для данных интервальной шкалы. Например, большинство температурных шкал (например, Цельсий, Фаренгейт и т. д.) являются интервальными шкалами с произвольными нулями, поэтому вычисленный коэффициент вариации будет отличаться в зависимости от используемой шкалы. С другой стороны, температура Кельвина имеет значимый нуль, полное отсутствие тепловой энергии, и, таким образом, является шкалой отношения. Говоря простым языком, имеет смысл сказать, что 20 кельвинов в два раза горячее, чем 10 кельвинов, но только в этой шкале с истинным абсолютным нулем. Хотя стандартное отклонение может быть измерено в Кельвинах, градусах Цельсия или Фаренгейта, вычисленное значение применимо только к этой шкале. Только шкала Кельвина может быть использована для вычисления действительного коэффициента вариации.Измерения, которые распределены логнормально, демонстрируют стационарный КВ; напротив, КОО изменяется в зависимости от ожидаемого значения измерений. Более надежной возможностью является квартильный коэффициент дисперсии, половина межквартильного диапазона делится на среднее значение квартилей . В большинстве случаев КВ вычисляется для одной независимой переменной (например, для одного фабричного продукта) с многочисленными повторяющимися измерениями зависимой переменной (например, ошибка в производственном процессе). Однако данные, которые являются линейными или даже логарифмически нелинейными и включают непрерывный диапазон для независимой переменной с разреженными измерениями по каждому значению (например, точечная диаграмма), могут поддаваться одиночному вычислению КВ с использованием подхода оценки максимального правдоподобия. Выборка называется однородной, если все её прецеденты одинаково распределены, то есть выбраны из одного и того же распределения. Независимая выборка. Выборка называется однородной, если все её прецеденты x_i,\; i=1,\ldots,m одинаково распределёны, то есть выбраны из одного и того же распределения \langle X^1,\Sigma^1,{\mathbb P}_1\rangle. |