высшая математика. 10 Обыкновенные диф-ые ур-ия. Контрольная работа. Контрольная работа 10 Обыкновенные дифференциальные уравнения. Задачи 112

• Название: Контрольная работа 10 Обыкновенные дифференциальные уравнения. Задачи 112
• Анкор: высшая математика
• Дата: 25.12.2022
• Размер: 1.81 Mb.
• Имя файла: 10 Обыкновенные диф-ые ур-ия. Контрольная работа.doc
• Тип: Контрольная работа; #863700
• страница: 3 из 7

Пример 5.

Решить уравнение Бернулли .

Приведем уравнение к виду



.

Обе части уравнения умножим на 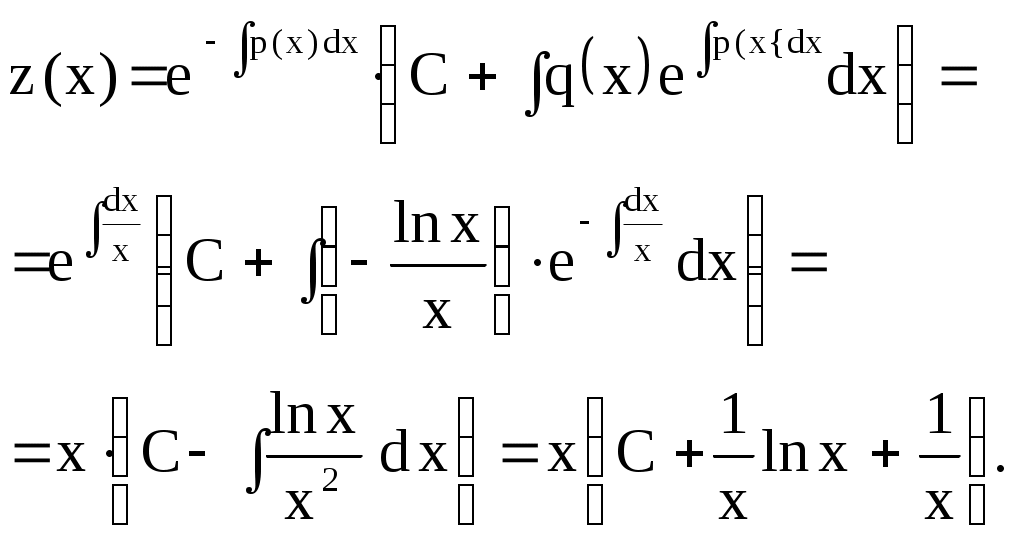и сделаем замену , причем, , получим - это линейное уравнение относительно .



Получили .

Поэтому .

Ответ: .

Упражнения. Решить уравнения

1. 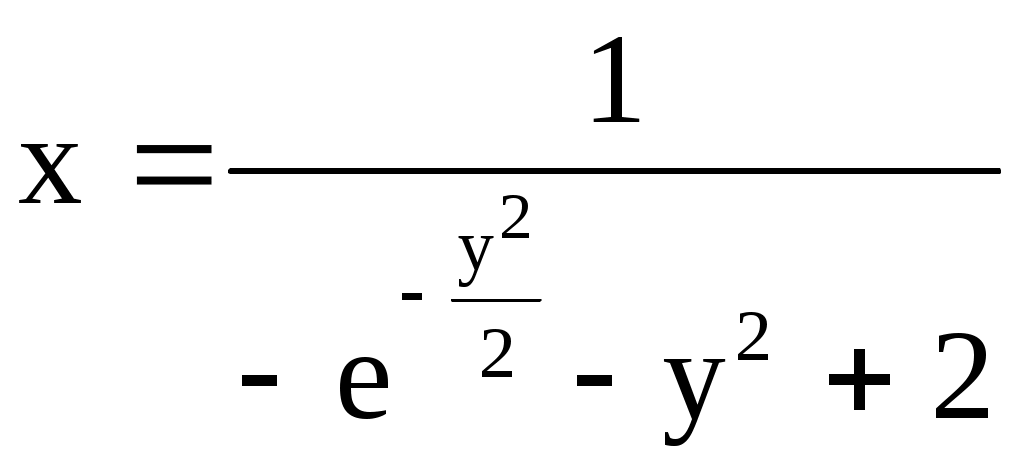. Ответ: .

2. . Ответ: .

3. . Ответ: .

Уравнение следует переписать в виде

или - это уравнение Бернулли относительно функции .

4. . Ответ: .

Обе части уравнения следует умножить на и сделать замену .

Контрольное задание № 4.

Решить уравнения Бернулли:

1.	.
2.	.
3.	.
4.	.
5.	.
6.	.
7.	.
8.	.
9.	.
10.	.
11.	.
12.	.
13.	.
14.	.
15.	.
16.	.
17.	.
18.	.
19.	.
20.	.
21.	.
22.	.
23.	.
24.	.
25.	.
26.	.
27.	.
28.	.
29.	.
30.	.

Задача 5. Уравнения в полных дифференциалах.

Дифференциальное уравнение вида

(1)

называется уравнением в полных дифференциалах, если его левая часть представляет полный дифференциал некоторой функции , т.е.

.

Для того, чтобы уравнение (1) являлось уравнением в полных дифференциалах, необходимо и достаточно, чтобы в некоторой области изменения переменных выполнялось условие

(2)

В этом случае общий интеграл имеет вид 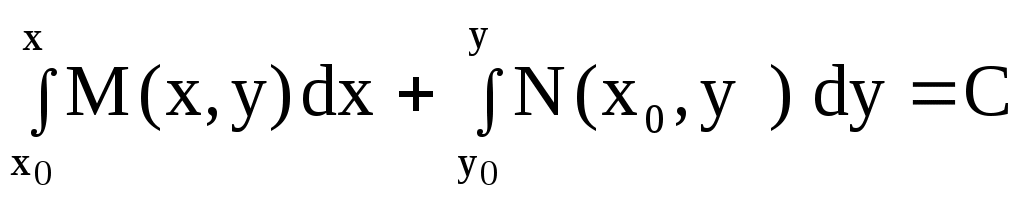или

.
Пример 6.

Решить уравнение .

Решение. Проверим является ли данное уравнение уравнением в полных дифференциалах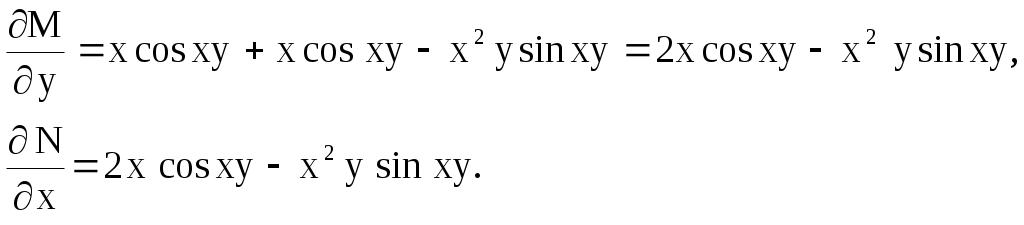

.



Получили, что , условие (2) выполнено, значит данное уравнение в полных дифференциалах.

Найдем функцию 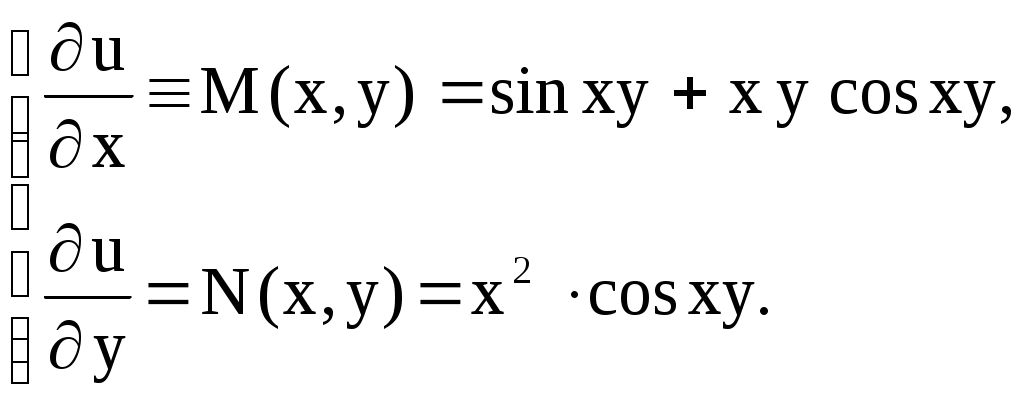. Для этого имеем систему:



Из первого уравнения, интегрированием по при постоянном , определяем :

,

где - произвольная функция (вместо постоянной интегрирования С берем функцию )

Частная производная , найденной функции должна равняться в силу второго уравнения системы, , что дает

,

.

Отсюда ,

- общий интеграл.

Ответ: , где .
Упражнения. Решить уравнения

1. . Ответ: .

2. . Ответ: .

3. . Ответ: .

4. . Ответ: .



,

уравнение в полных дифференциалах.

Контрольное задание № 5.

Проинтегрировать уравнения в полных дифференциалах:

1.	.
2.	.
3.	.
4.	.
5.	.
6.	.
7.	.
8.	.
9.	.
10.	.
11.	.
12.	.
13.	.
14.	.
15.	.
16.	.
17.	.
18.	.
19.	.
20.	.
21.	.
22.	.
23.	.
24.	.
25.	.
26.	.
27.	.
28.	.
29.	.
30.	.