Электронный конспект по программированию часть 1. Программа на языке Си, так же как и на большинстве современных языков программирования, создается в два этапа
 Скачать 32.35 Mb. Скачать 32.35 Mb.
|
|
int **A; Но лучше всего сразу объявить новый тип данных - указатель на целое число. Новые типы объявляются директивой typedef вне всех процедур и функций (там же, где и глобальные переменные). typedef int *pInt; Этой строкой мы сказали компилятору, что любая переменная нового типа pInt представляет собой указатель на целое число или адрес массива целых чисел. К сожалению, место для матрицы не удается так же просто выделить в памяти, как мы делали это для одномерного массива. Если написать просто int M = 5, N = 7; pInt *A; A = new int[M][N]; // ошибочнаястрока компилятор выдает множество ошибок. Связано это с тем, что ему требуется заранее знать длину одной строки, чтобы правильно расшифровать запись типа A[i][j]. Ниже рассмотрены три способа решения этой проблемы. Известный размер строки Если размер строки матрицы известен, а неизвестно только количество строк, можно по- ступить так: ввести новый тип данных – строка матрицы. Когда количество строк станет известно, с помощью оператора new выделяем массив таких данных. typedef int row10[10]; // новы тип: массив из 10 элементов main() { int N; row10 *A; // указатель на массив (матрица) printf ( "Введите число строк "); scanf ( "%d", &N ); A = new row10[N]; // выделить память на N строк A[0][1] = 25; // используем матрицу, как обычно printf("%d", A[2][3]); delete A; // освобождаем память } Неизвестный размер строки Пусть размеры матрицы M и N заранее неизвестны и определяются в ходе работы про- граммы. Тогда можно предложить следующий способ выделения памяти под новую матрицу. Поскольку матрицу можно рассматривать как массив из строк-массивов, объявим M указателей и выделим на каждый из них область памяти для одномерного массива размером N (то есть, на одну строку). Сами эти указатели тоже надо представить в виде динамического массива. Определив требуемые размеры матрицы, мы выделяем сначала динамический массив указателей, а потом на каждый указатель – место для одной строки. typedef int *pInt; // новый тип данных: указатель на целое main() { intM, N, i; pInt *A; // указатель на указатель // ввод M и N A = new pInt[M]; // выделить память под массив указателей for ( i = 0; i < M; i ++ ) // цикл по всем указателям A[i] = new int[N]; // выделяем память на строку i // работаем с матрицей A, как обычно for ( i = 0; i < M; i ++ ) // освобождаем память для всех строк delete A[i]; delete A; // освобождаем массив указателей } В рассмотренном выше случае на каждую строку выделяется свой участок памяти. Можно поступить иначе: сначала выделим область памяти сразу на всю матрицы и запишем ее адрес в A[0]. Затем расставим указатели так, чтобы A[1] указывал на N+1-ый элемент с начала блока(начало строки 1), A[2] – на 2N+1-ый (начало строки 2) и т.д. Таким образом, в памяти выделяется всего два блока – массив указателей и сама матрица. typedef int *pInt; main() { int M, N, i; pInt *A; // указательнауказатель // ввод M и N A = new pInt[M]; // память на массив указателей A[0] = new int [M*N]; // память для матрицы for ( i = 1; i < M; i ++ ) // расставляем указатели A[i] = A[i-1] + N; // работаем с матрицей delete A[0]; // освобождаем матрицу delete A; // освобождаем указатели } 6. Рекурсия Что такое рекурсия? Рекурсивные объекты Всем известна сказка, которая начинается словами «У попа была собака...». Это бесконеч- ное предложение будем называть сказкой о попе и собаке. Как же нам определить его строго математически? Оказывается, это можно сделать примерно так:  Как видите, частью этой сказки является сама сказка. Так мы пришли к понятию рекурсии. Еще один пример – картинка, содержащая свое изображение.  Рекурсия – это определение объекта через самого себя. С помощью рекурсии в математике определяются многие бесконечные множества, например множество натуральных чисел. Действительно, можно задать их так: Натуральное число. 1) 1 - натуральное число. 2) Число, следующее за натуральным – натуральное. Понятие факториала n!=1·2·3·…·(n-1) ·n также можно задать рекурсивно: Факториал. 1) 0! = 1 (так условно принято). 2) n! = n*(n-1)! Рекурсивные процедуры и функции Причем же здесь программирование? Оказывается, процедуры и функции в современных языках программирования также могут вызывать сами себя. Рекурсивными называются процедуры и функции, которые вызывают сами себя. Например, функцию вычисления факториала можно записать так: int Factorial ( int n ) { if ( n <= 0 ) return 1; // вернуть 1 else return n*Factorial(n-1); // рекурсивныйвызов } Обратите внимание, что функция Factorial вызывает сама себя, если n > 0. Для решения этой задачи можно использовать и рекурсивную процедуру (а не функцию). Вспомним, как рекурсивная процедура может вернуть значение-результат? Через параметр, переданный по ссылке (в объявлении процедуры у его имени стоит знак ссылки &). При рекурсивных вызовах процедура меняет это значение. void Factorial ( int n, int &fact ) { if ( n == 0 ) fact = 1; // рекурсия закончилась else { Factorial(n-1, fact); // рекурсивный вызов, считаем (n-1)! fact *= n; // n! = n*(n-1)! } } В отличие от функции, процедура может (если надо) возвращать несколько значений- результатов с помощью параметров, передаваемых по ссылке. Косвенная рекурсия Реже используется более сложная конструкция, когда процедура вызывает сама себя не напрямую, а через другую процедуру (или функцию). Это описывается следующей схемой: 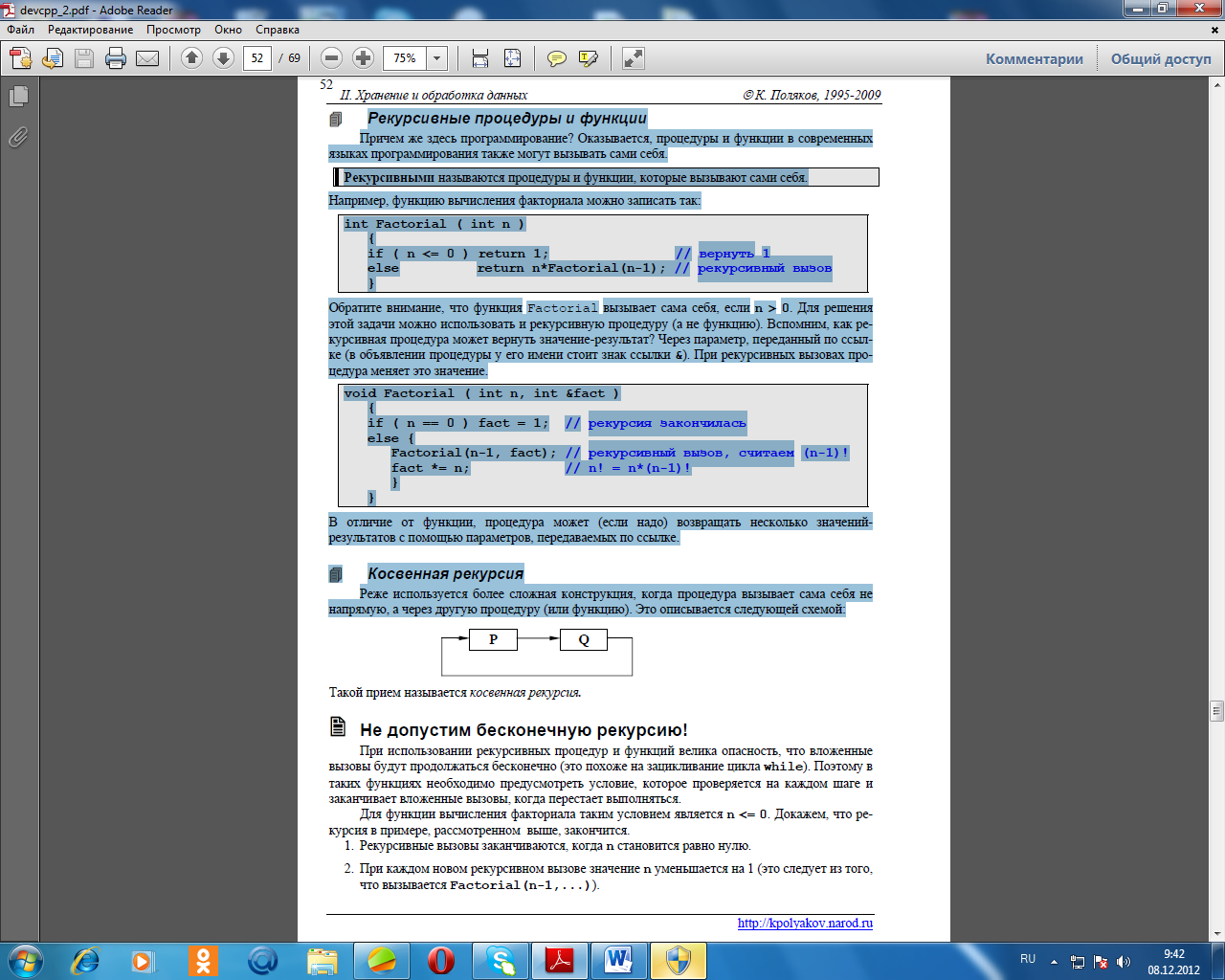 Не допустим бесконечную рекурсию! При использовании рекурсивных процедур и функций велика опасность, что вложенные вызовы будут продолжаться бесконечно (это похоже на зацикливание цикла while). Поэтому в таких функциях необходимо предусмотреть условие, которое проверяется на каждом шаге и заканчивает вложенные вызовы, когда перестает выполняться. Для функции вычисления факториала таким условием является n <= 0. Докажем, что рекурсия в примере, рассмотренном выше, закончится. 1. Рекурсивные вызовы заканчиваются, когда n становится равно нулю. 2. При каждом новом рекурсивном вызове значение n уменьшается на 1 (это следует из того,что вызывается Factorial(n-1,...)). 3. Поэтому, если в началеn > 0, то, постепенно уменьшаясь, n достигает значения 0 и рекурсия заканчивается. Рекурсивная процедура или функция должна содержать условие, при котором рекурсия заканчивается (не происходит нового вложенного вызова). Когда рекурсия не нужна При новом рекурсивном вызове компьютер делает так: 1. Запоминается состояние вычислений на данном этапе. 2. В стеке (особой области памяти) создается новый набор локальных переменных (чтобы не испортить переменные текущего вызова). Поскольку при каждом вызове затрачивается новая память и расходуется время на вызов процедуры и возврат из нее, при использовании рекурсии необходимо помнить, что глубина рекурсии (количество вложенных вызовов) должна была достаточно мала. Программа, использующая рекурсию с большой глубиной, будет выполняться долго и может вызвать переполнение стека (нехватку стековой памяти). Поэтому если задача может быть легко решена без использования рекурсии, рекурсию использовать нежелательно. Например, задача вычисления факториала очень просто решается с помощью обычного цикла for (такое решение с помощью циклов называют итеративным, циклическим): int Factorial ( int n ) { int i, fact = 1; for ( i = 2; i <= n; i ++ ) fact *= i; return fact; } Эта функция работает намного быстрее, чем рекурсивная. Доказано, что любая рекурсивная программа может быть написана без использования рекурсии, хотя такая реализация может оказаться очень сложной. Задача. Составить функцию для вычисления чисел Фибоначчи fi, которые задаются так: 1. f0= 0, f1 = 1. 2. fi= fi-1 + fi-2 дляi > 1. Использование рекурсии «в лоб» дает функцию int Fib ( int n ) { if ( n == 0 ) return 0; if ( n == 1 ) return 1; return Fib(n-1) + Fib(n-2); } Заметим, что каждый рекурсивный вызов при n > 1 порождает еще 2 вызова функции, многие выражения (числа Фибоначчи для малых n) вычисляются много раз. Поэтому практического значения этот алгоритм не имеет, особенно для большихn. Схема вычисления Fib(5) показана в виде дерева ниже: 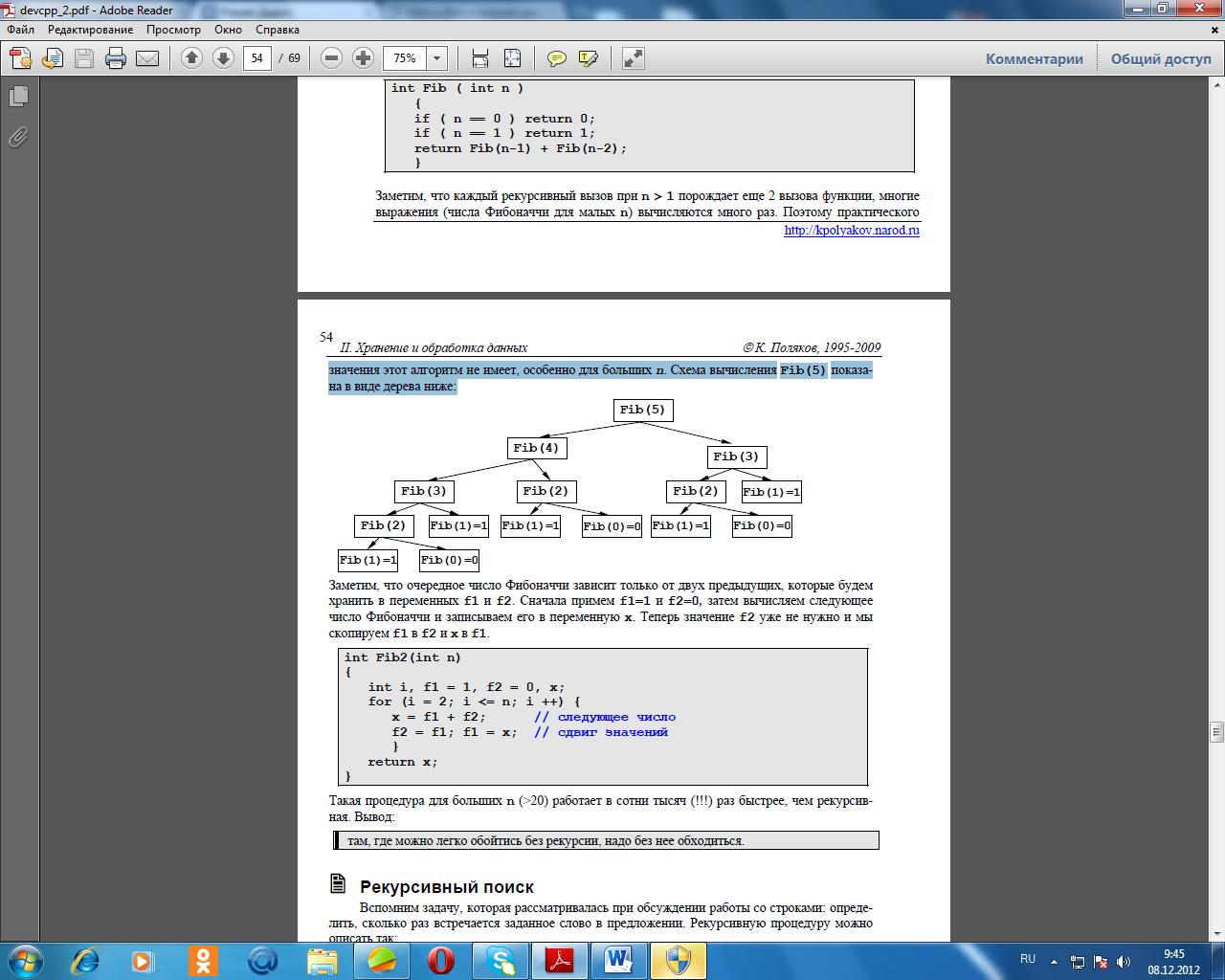 Заметим, что очередное число Фибоначчи зависит только от двух предыдущих, которые будем хранить в переменных f1 и f2. Сначала примем f1=1 и f2=0, затем вычисляем следующее число Фибоначчи и записываем его в переменную x. Теперь значение f2 уже не нужно и мы скопируем f1 в f2 и x в f1. int Fib2(int n) { int i, f1 = 1, f2 = 0, x; for (i = 2; i <= n; i ++) { x = f1 + f2; // следующеечисло f2 = f1; f1 = x; // сдвиг значений } return x; } Такая процедура для больших n (>20) работает в сотни тысяч (!!!) раз быстрее, чем рекурсивная. Вывод: там, где можно легко обойтись без рекурсии, надо без нее обходиться. Рекурсивный поиск Вспомним задачу, которая рассматривалась при обсуждении работы со строками: опреде- лить, сколько раз встречается заданное слово в предложении. Рекурсивную процедуру можно описать так: 1) ищем первое заданное слово с помощью функции strstr; если не нашли, то стоп; 2) количество слов = 1 + количество слов в оставшейся части строки. int HowMany( char *s, char *word ) { char *p = strstr(s, word); // ищемпервоеслово if ( ! p ) return 0; // ненашли – 0 слов return 1 + // одноуженашли, ... HowMany(p+strlen(word),word); // ищемдальше } Функция получилась короткая, понятная, но по скорости работы не самая эффективная. Рекурсивные фигуры Многие рисунки и кривые задаются рекурсивно. Рассмотрим сначала простейший пример. В центре рисунка – большая окружность. На ней находятся центры четырех окружностей меньшего диаметра, на каждой из которых – центры еще четырех окружно- стей еще меньшего диаметра и т.д. Всего – N разных диаметров (N уровнейрекурсии). void RecCircle ( float x, float y, float R, int n ) { float k = 0.5; circle ( x, y, R ); // рисуемокружность if ( n == 1 ) return; // все нарисовали, выход RecCircle( x+R, y, k*R, n-1); // четыре рекурсивных вызова RecCircle( x-R, y, k*R, n-1); RecCircle( x, y+R, k*R, n-1); RecCircle( x, y-R, k*R, n-1); } Процедура для рисования такой фигуры принимает 4 параметра – координаты центра базовой окружности (x,y), ее радиус R и количество уровней n, которые надо нарисовать. На следующем уровне радиус изменяется в k раз (в примере – k=0.5), количество оставшихся уровней уменьшается на 1, и пересчитываются координаты для 4-х окружностей следующего уровня.Важно доказать, что рекурсия закончится. В самом деле, как видно из процедуры, при n = 1 рекурсия заканчивается. При каждом новом рекурсивном вызове количество уровней n уменьшается на 1, поэтому если в самом начале n > 0, то оно достигнет значения 1 и рекурсия завершится. Для большей «защиты от дурака» лучше условие окончания рекурсии записать так: if ( n <= 1 ) return; Если этого не сделать, рекурсия никогда не завершится (теоретически), если в начале задали n < 1. Основная программа получается очень короткой – в ней надо открыть окно для графики, и один раз вызвать процедуру RecCircle. #include #include // сюда надо вставить процедуру main() { initwindow(600, 500); RecCircle ( 300, 250, 100, 3 ); // 3 уровня getch(); closegraph(); } Пифагорово дерево задается так: «ствол» дерева – вертикаль-ный отрезок длиной l. От него вверх симметрично отходят две ветки так, чтобы угол между ними был 90 градусов, их длина равна k*l, где k<1. Так повторяется для заданного количества уровней. На рисунке показано дерево Пифагора при k=0.7, имеющее 5 уровнейЧтобы написать процедуру, придется вспомнить геометрию и тригонометрию. Проще всего получается, если написать формулы для произвольного угла наклона ветки α. Если (x,y) – координаты начала ветки и она наклонена по отношению к горизонту на угол α, то формулы для определения координат конца ветки (x1,y1) принимают вид: x1 = x + L * cos(α) y1 = y - L * sin(α) 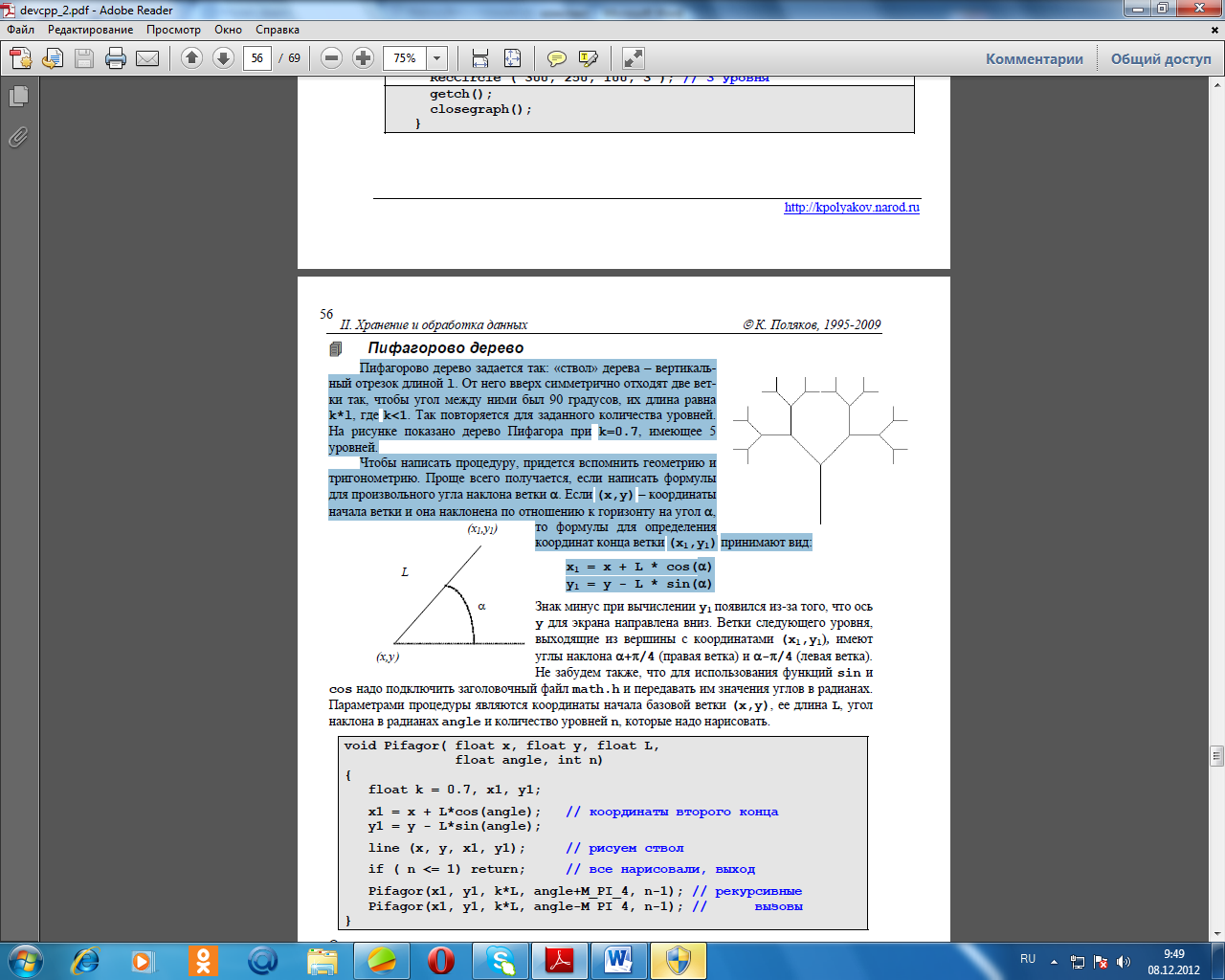 Знак минус при вычислении y1 появился из-за того, что ось y для экрана направлена вниз. Ветки следующего уровня,выходящие из вершины с координатами (x1,y1), имеют углы наклона α+π/4 (правая ветка) и α-π/4 (левая ветка). Не забудем также, что для использования функций sin и cos надо подключить заголовочный файл math.h и передавать им значения углов в радианах.Параметрами процедуры являются координаты начала базовой ветки (x,y), ее длина L, угол наклона в радианах angle и количество уровней n, которые надо нарисовать. void Pifagor( float x, float y, float L, float angle, int n) { float k = 0.7, x1, y1; x1 = x + L*cos(angle); // координаты второго конца y1 = y - L*sin(angle); line (x, y, x1, y1); // рисуем ствол if ( n <= 1) return; // все нарисовали, выход Pifagor(x1, y1, k*L, angle+M_PI_4, n-1); // рекурсивные Pifagor(x1, y1, k*L, angle-M_PI_4, n-1); // вызовы } Основная программа выглядит примерно так же, как и в предыдущем примере. Перебор вариантов Одна из главных практически важных областей, где применение рекурсии значительно упрощает решение – задачи на перебор вариантов. Сочетания Необходимо получить все возможные сочетания чисел от 1 до K, которые имеют длину N (в последовательности могут быть одинаковые элементы). Для решения задачи выделим в памяти массив A[N]. Представим себе, что все его первые q элементов (с номерами от 0 до q-1) уже определены, и надо найти все сочетания, при которых эти элементы не меняются. Сначала ставим на место элемент с номером q. По условию на этом месте может стоять любое число от 1 до K, поэтому сначала ставим 1 и находим все варианты, при которых q+1 элементов уже поставлены (здесь будет рекурсивный вызов), затем ставим на это место 2 и т.д. Если q=N, то все элементы уже поставлены на место, и надо печатать массив –одна из нужных комбинаций готова. Ниже приведена рекурсивная процедура, которая использует массив A[N] и печатает все комбинации на экране. |
