Электронный конспект по программированию часть 1. Программа на языке Си, так же как и на большинстве современных языков программирования, создается в два этапа
 Скачать 32.35 Mb. Скачать 32.35 Mb.
|
|
void Combinations ( int A[], int N, int K, int q ) { if ( q == N ) // одна комбинация получена PrintData ( A, N ); else for (int i = 1; i <= K; i ++ ) { A[q] = i; Combinations(A, N, K, q+1); // рекурсивныйвызов } } Для вывода массива на экран используется такая процедура: void PrintData ( int Data[], int N ) { for (int i = 0; i < N; i++ ) printf("%2d ", Data[i]); printf("\n"); } В основной программе надо вызвать процедуру с параметром q = 0, поскольку ни один элемент еще не установлен: #include // здесь надо разместить процедуры main() { int A[5], N = 5, K = 10; Combinations ( A, N, K, 0 ); } Перестановки Существует еще одна весьма непростая задача, которая хорошо решается с помощью ре- курсии. Представьте, что к вам пришли N гостей. Сколько существует различных способов рассадить их за столом?Сформулируем условие задачи математически. В массиве A[N] записаны целые числа.Надо найти все возможные перестановки этих чисел (в перестановку должны входить все элементы массива по 1 разу)Как и в предыдущем примере, предположим, что q элементов массива (с номерами от 0 до q-1) уже стоят на своих местах. Тогда в позиции q может стоять любой из неиспользованных элементов – их надо перебрать в цикле и вызвать рекурсивно эту же процедуру, увеличив на 1 количество установленных элементов. Чтобы не потерять никакой элемент, в цикле для всех i от q до N-1 будем переставлять элементы A[i] и A[q], генерировать все возможные комбинации, а затем менять их местами, восстанавливая исходный порядок. Для обмена местами двух элементов массива будем использовать вспомогательную пере- меннуюtemp. void Permutations ( int A[], int N, int q ) { int temp; if ( q == N ) // перестановка получена PrintData ( A, N ); // вывод на экран else for (int i = q; i <= N; i ++ ) { temp = A[q]; A[q] = A[i]; A[i] = temp; // A[q]<->A[i] Permutations(A, N, q+1); // рекурсивныйвызов temp = A[q]; A[q] = A[i]; A[i] = temp; // A[q]<->A[i] } } Разложение числа на сумму слагаемых Пример. Дано целое число S. Требуется получить и вывести на экран все возможные различные способы представления этого числа в виде суммы натуральных чисел (то есть, 1 + 2 и 2 + 1– это один и тот же способ разложения числа 3).Самое сложное в этой задаче – сразу исключить из рассмотрения повторяющиеся последовательности. Для этого будем рассматривать только неубывающие последовательности слагаемых(каждое следующее слагаемое не меньше предыдущего).Все слагаемые будем записывать в массив. Для этого нам понадобится массив (назовемего A) из S элементов, поскольку самое длинное представление – это сумма S единиц. Чтобы нерасходовать память зря, лучше выделять его динамически (см. раздел про массивы).Пусть q элементов массива (с номерами от 0 до q-1) уже стоят на своих местах, причемA[q-1]=m. Каким может быть следующее слагаемое – элемент A[q]? Поскольку последовательность неубывающая, он не может быть меньше m. С другой стороны, он должен быть небольше, чем R=S-S0, где S0 – сумма предыдущих элементов.Эти размышления приводят к следующей процедуре, которая принимает в параметрахсумму оставшейся части, массив для записи результата и количество уже определенных элементов последовательности. void Split(int R, int A[], int q) { int i, start = 1; if ( R <= 0 ) { PrintData ( A, q ); return; } if ( q > 0 ) start = A[q-1]; // новыйэлементнеменьше A[q-1] for (i = start; i <= R; i ++ ) { // перебратьвседо R A[q] = i; Split(R-i, A, q+1); // рекурсивныйвызов } } Основная программа вызывает эту процедуру так (используется динамический массив): #include // здесь надо поместить процедуры Split и PrintData main() { int *A, S; printf ( "Введите натуральное число " ); scanf ( "%d", &S ); A = new int[S]; // выделитьпамять Split (S, A, 0); // получить все разложения delete A; // освободить память } Быстрая сортировка (QuickSort) Один из лучших известных методов сортировки массивов – быстрая сортировка Ч. Хоа- ра (Quicksort) основана как раз на применении рекурсии.Будем исходить из того, что сначала лучше делать перестановки элементов массива на большом расстоянии. Предположим, что у нас есть n элементов и известно, что они уже отсортированы в обратном порядке. Тогда за n/2 обменов можно отсортировать их как надо – сначала поменять местами первый и последний, а затем последовательно двигаться с двух сторон. Хотя это справедливо только тогда, когда порядок элементов в самом деле обратный, подобная идея заложена в основу алгоритма Quicksort.Пусть дан массив A из n элементов. Выберем сначала наугад любой элемент массива (назовем его x). Обычно выбирают средний элемент массива, хотя это не обязательно. На первом этапе мы расставим элементы так, что слева от некоторой границы находятся все числа, меньшие или равные x, а справа – большие или равные x. Заметим, что элементы, равные x, могут находиться в обеих частях. A[i] <= x A[i] >= x Теперь элементы расположены так, что ни один элемент из первой группы при сортировке не окажется во второй и наоборот. Поэтому далее достаточно отсортировать отдельно каждую часть массива. Размер обеих частей чаще всего не совпадает. Лучше всего выбирать x так, чтобы в обеих частях было равное количество элементов. Такое значение x называется медианой массива. Однако для того, чтобы найти медиану, надо сначала отсортировать массив, то есть заранее решить ту самую задачу, которую мы собираемся решить этим способом. Поэтому обычно в качестве x выбирают средний элемент массива. Будем просматривать массив слева до тех пор, пока не обнаружим элемент, который больше x (и, следовательно, должен стоять справа от x), потом справа пока не обнаружим элемент меньше x (он должен стоять слева от x). Теперь поменяем местами эти два элемента и продолжим просмотр до тех пор, пока два «просмотра» не встретятся где-то в середине массива. В результате массив окажется разбитым на 2 части: левую со значениями меньшими или равными x, и правую со значениями большими или равными x. Затем такая же процедура применяется к обеим частям массива до тех пор, пока в каждой части не останется один элемент (и таким образом, массив будет отсортирован). Чтобы понять сущность метода, рассмотрим пример. Пусть задан массив__ 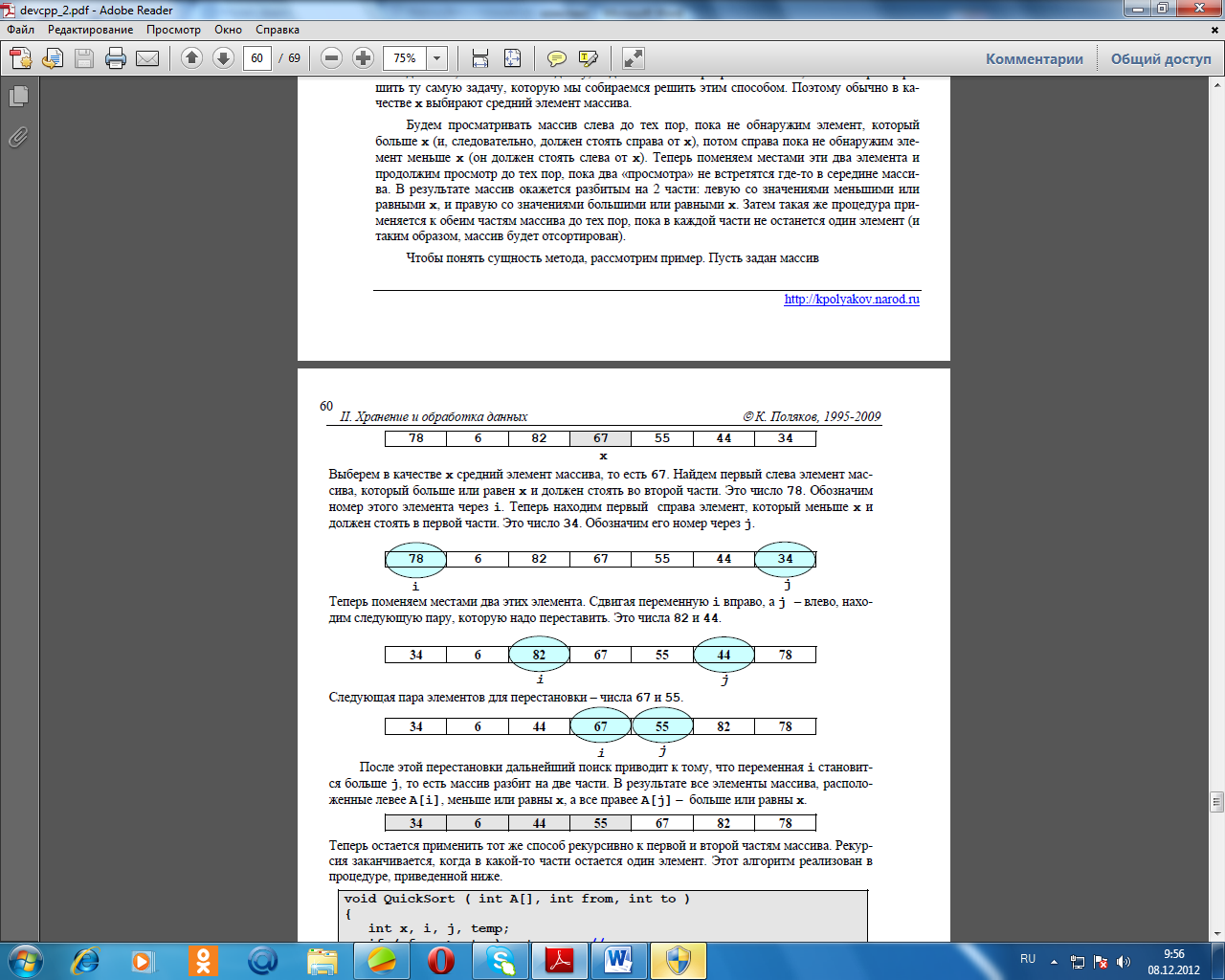 После этой перестановки дальнейший поиск приводит к тому, что переменная i становит- ся больше j, то есть массив разбит на две части. В результате все элементы массива, расположенные левее A[i], меньше или равны x, а все правее A[j] – больше или равны x. 34 6 44 55 67 82 78 Теперь остается применить тот же способ рекурсивно к первой и второй частям массива. Рекурсия заканчивается, когда в какой-то части остается один элемент. Этот алгоритм реализован в процедуре, приведенной ниже. void QuickSort ( int A[], int from, int to ) { int x, i, j, temp; if ( from >= to ) return; // условие окончания рекурсии i = from; // рассматриваем элементы с A[from] до A[to] j = to; x = A[(from+to)/2]; // выбралисреднийэлемент while ( i <= j ) { while ( A[i] < x ) i ++; // ищем пару для перестановки while ( A[j] > x ) j --; if ( i <= j ) { temp = A[i]; A[i] = A[j]; A[j] = temp; // перестановка i ++; // двигаемсядальше j --; } } QuickSort ( A, from, j ); // сортируемлевуючасть QuickSort ( A, i, to ); // сортируем правую часть } Насколько эффективна такая сортировка? Все описанные ранее способы сортировки массивов имели порядок O(n2), то есть при увеличении в 10 раз длины массива время сортировки увеличивается в 100 раз. Можно показать, что Quicksort имеет в среднем порядок O(n·log n), что значительно лучше. Чтобы почувствовать, что такое O(n·log n) и O(n2), посмотрите на таблицу, где приведены числа, иллюстрирующие скорость роста для нескольких разных функций. 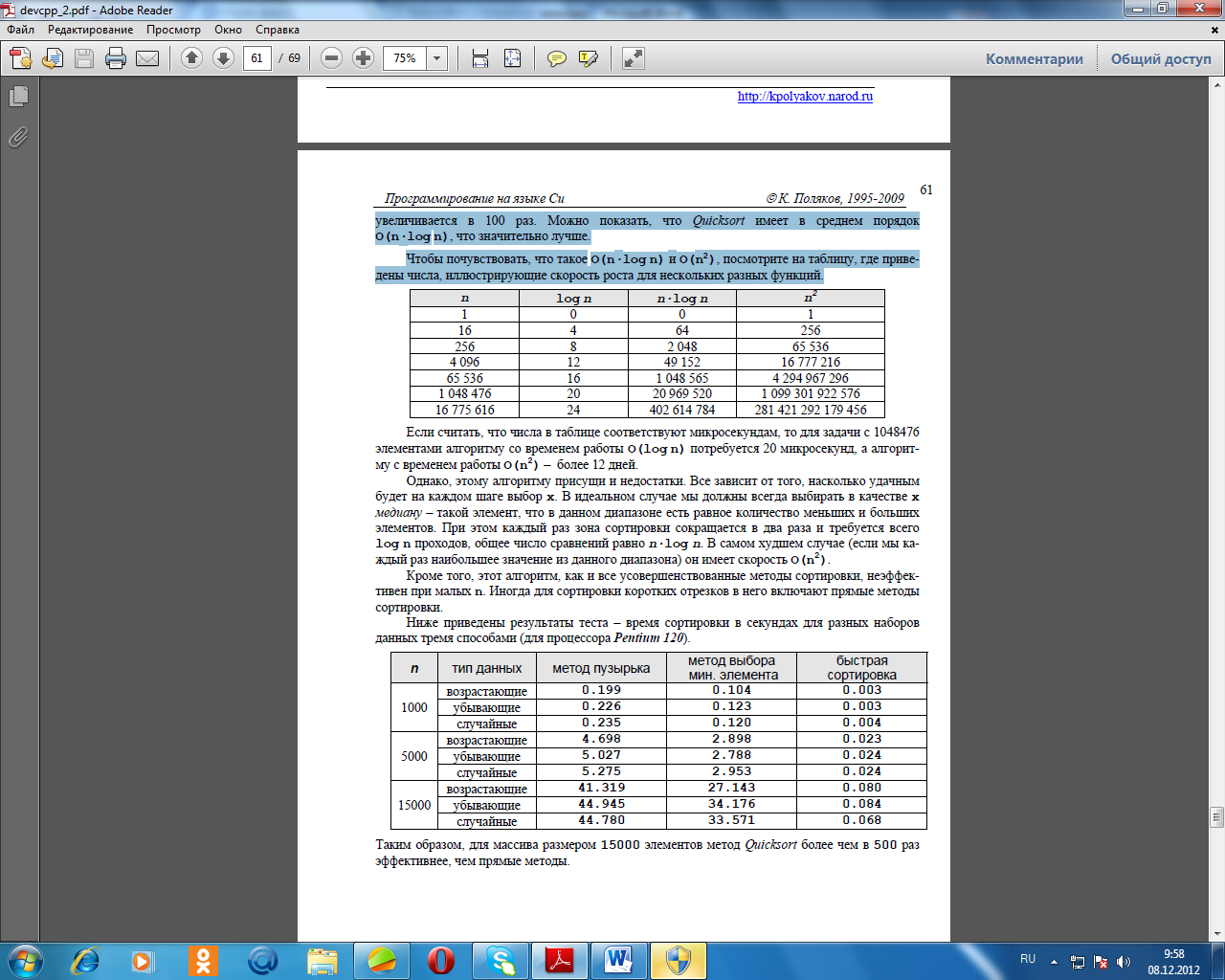 Если считать, что числа в таблице соответствуют микросекундам, то для задачи с 1048476 элементами алгоритму со временем работы O(log n) потребуется 20 микросекунд, а алгоритму с временем работы O(n2) – более 12 дней.Однако, этому алгоритму присущи и недостатки. Все зависит от того, насколько удачным будет на каждом шаге выбор x. В идеальном случае мы должны всегда выбирать в качестве xмедиану – такой элемент, что в данном диапазоне есть равное количество меньших и больших элементов. При этом каждый раз зона сортировки сокращается в два раза и требуется всего log n проходов, общее число сравнений равно n·log n. В самом худшем случае (если мы каждый раз наибольшее значение из данного диапазона) он имеет скорость O(n2). Кроме того, этот алгоритм, как и все усовершенствованные методы сортировки, неэффективен при малых n. Иногда для сортировки коротких отрезков в него включают прямые методы сортировки.Ниже приведены результаты теста – время сортировки в секундах для разных наборов данных тремя способами (для процессора Pentium 120).  Таким образом, для массива размером 15000 элементов метод Quicksort более чем в 500 раз эффективнее, чем прямые методы. 7. Структуры Что такое структуры? Очень часто при обработке информации приходится работать с блоками, в которых присутствуют разные типы данных. Например, информация о книге в каталоге библиотеки включает в себя автора (символьная строка), название книги (тоже строка), год издания (целое число),количество страниц (целое число) и т.п. Для хранения этой информации в памяти не подходит обычный массив, так как в массиве все элементы должны быть одного типа. Конечно, можно использовать несколько массивов разных типов, но это не совсем удобно (желательно, чтобы все данные о книге находились в памяти в одном месте). В современных языках программирования существует особый тип данных, который может включать в себя несколько элементов более простых (причем разных!) типов. Структура – это тип данных, который может включать в себя несколько полей – элементов разных типов (в том числе и другие структуры). Одно из применений структур – организация различных баз данных, списков и т.п. Объявление и инициализация Поскольку структура - это новый тип данных, его надо предварительно объявить в начала программы, например так struct Book { char author[40]; // автор, символьная строка char title[80]; // название, символьная строка int year; // год издания, целое число int pages; // количество страниц, целое число }; При таком объявлении типа никакая память не выделяется, реальных структур в памяти еще нет. Этот фрагмент просто скажет компилятору, что в программе могут быть элементы такого типа. Теперь, когда надо выделить память, мы напишем Book b; Это оператор выделяет место в памяти под одну структуру типа Book и дает ей имя b (таким образом, Book – это названия типа данных (как int или float), а b – это имя конкретного экземпляра). При этом можно сразу записать в память нужное начальное значение всех или нескольких первых элементов структуры в фигурных скобках через запятую. Поля заполняются последовательно в порядке их объявления. Память, отведенная на поля, оставшиеся __________незаполненными, обнуляется. Book b = { "А. С. Пушкин", "Полтава", 1998 }; Работа с полями структуры Обращение по имени Для обращения ко всей структуре используется ее имя, а для обращения к отдельному полю имя этого поля ставится через точку. Элементы структуры вводятся последовательно по одному. Заполнять их можно в любом порядке. С полем структуры можно работать так же, как и с переменной соответствующего типа: числовые переменные могут участвовать в арифметических выражениях, со строками можно выполнять все стандартные операции. Book b; strcpy ( b.author, " А.С. Пушкин " ); b.year = 1998; ��Обращение по адресу Пусть известен адрес структуры в памяти. Как известно, адрес может быть записан в указатель – специальную переменную для хранения адреса. Для обращения к полю структуры по ее адресу используют специальный оператор ->. Book b; // структура в памяти Book *p; // указатель на структуру p = &b; // записать адрес структуры в указатель strcpy ( p->author, "А.С. Пушкин" ); // обращение по адресу p->year = 1998; Ввод и вывод Поэлементный ввод и вывод При вводе с клавиатуры и выводе на экран или в текстовый файл с каждым полем струк- туры надо работать отдельно, как с обычной переменной. В приведенном примере данные вводятся в структуру b типа Book с клавиатуры и записываются в конец текстового файла books.txt. Book b; FILE *fp; printf("Автор "); gets(b.author); printf("Название книги "); gets(b.title); printf("Год издания, кол-во страниц "); scanf("%d%d", &b.years, &b.pages ); fp = fopen("books.txt", "a"); // дописать в конец файла fprintf(fp, "%s\n%s\n%d %d\n", b.author, b.title, b.years, b.pages ); fclose ( fp ); Работа с двоичным файлом Структуры очень удобно записывать в двоичные файлы, поскольку можно за 1 раз прочи- тать или записать сразу одну или даже несколько структур. Вспомним, что при чтении из дво- ичного файла функции fread надо передать адрес нужной области памяти (куда записать про- читанные данные), размер одного блока и количество таких блоков. Для того, чтобы не вычис- лять размер структуры вручную (можно легко ошибиться), применяют оператор sizeof. Book b; int n; FILE *fp; fp = fopen("books.dat", "rb"); n = fread (&b, sizeof(Book), 1, fp); if ( n == 0 ) { printf ( "Ошибка при чтении из файла" ); } fclose ( fp ); Можно было также вместо sizeof(Book) написать sizeof(b), поскольку запись b – это как раз один экземпляр структуры Book. Функция fread возвращает число удачно прочитанных элементов (в нашем случае – структур). Поэтому если в примере переменная n равно нулю,чтение закончилось неудачно и надо вывести сообщение об ошибке. Для записи структуры в двоичный файл используют функцию fwrite. Ее параметры – те же, что и у fread. Пример ниже показывает добавление структуры в конец двоичного файла books.dat. Book b; FILE *fp; // здесь надо заполнить структуру fp = fopen("books.dat ", "ab"); fwrite(&b, sizeof(Book), 1, fp); fclose ( fp ); Копирование Пример. Пусть в памяти выделено две структуры одного типа и в одну из них записаны какие-то данные. Требуется скопировать все данные из первой структуры во вторую. Пусть структуры имеют тип Book и называются b1 и b2. Существуют три способа решения этой задачи. Самый сложный – копирование каждого поля отдельно: Book b1, b2; // здесь заполняем структуру b1 |
