Задание 2_Лейченко Ю.С.. Программа среднего профессионального образования Право и организация социального обеспечения Дисциплина Статистика

• Название: Программа среднего профессионального образования Право и организация социального обеспечения Дисциплина Статистика
• Дата: 24.04.2023
• Размер: 53.01 Kb.
• Имя файла: Задание 2_Лейченко Ю.С. .docx
• Тип: Программа; #1084753

Автономная некоммерческая организация профессионального образования «Открытый социально- экономический колледж»


Программа среднего профессионального образования

Право и организация социального обеспечения

Дисциплина: Статистика

Практическое задание № 2


Выполнил:

слушатель: Лейченко Юлия Сергеевна

Преподаватель:

Семенова Наталья Александровна

Задание 1

В таблице  имеются данные об общей численности пенсионеров РФ в исследуемые годы.

год	1995	2000	2005	2007	2008
Численность пенсионеров (тыс. чел.)	37083	38411	38313	38467	38598

Используя данные таблицы 3, выполните задания:

1. Определите вид статистического ряда, представленного в таблице.

2. По данным таблицы определите основные показатели динамики.

3. Определите среднюю численность пенсионеров в исследуемый период. Обоснуйте  применённую Вами формулу.

4. По данным таблицы постройте динамический график численности пенсионеров в исследуемый период.

Решение:

1. Статистического ряд, представленный в таблице представляет собой ряд динамики.
   
   
   
2. По данным таблицы определите основные показатели динамики.
   Важнейшим статистическим показателем анализа динамики  яв­ляется абсолютный прирост (сокращение), т.е. абсолютное изменение, характеризующее увеличение или уменьшение уровня ряда за определённый промежуток времени. Абсолютный прирост с пере­менной базой называют скоростью роста.
   Абсолютные приросты вычисляются по формулам:
    (цепной)
    (базисный)
   где yi — уровень сравниваемого периода; yi-1— уровень предшествующего периода; У0 — уровень базисного периода.
   Для оценки интенсивности, т. е. относительного изменения уровня динамического ряда за какой-либо период времени ис­числяют темпы роста (снижения).
   Интенсивность изменения уровня оценивается отношением отчетного уровня к базисному.
   Показатель интенсивности изменения уровня ряда, выра­женный в долях единицы, называется коэффициентом роста, а в процентах — темпом роста. Эти показатели интенсивности из­менения отличаются только единицами измерения.
   Коэффициент роста (снижения) показывает, во сколько раз сравниваемый уровень больше уровня, с которым произ­водится сравнение (если этот коэффициент больше единицы) или какую часть уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы). Темп роста всегда представляет собой положительное число.
   Коэффициент роста вычисляются по формулам:
   (цепной)
     (базисный)
   Темпы  роста:
    (цепной)
     (базисный)
   Темпы  прироста:
    (цепной)
     (базисный)
   Абсолютное значение одного процента прироста Ai . Этот показатель служит косвенной мерой базисного уровня. Представляет собой одну сотую часть базисного уровня, но одновременно представляет собой и отношение абсолютного прироста к соответствующему темпу роста.
   Данный показатель рассчитывают по формуле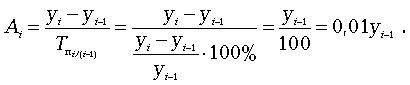
   
   
   
   

Расчеты показателей оформим в таблице.
Таблица 3

Годы	Численность пенсионеров, тыс. чел.	Абсолютные приросты,                  тыс. чел.		Коэффициенты роста			Темпы роста, %			Темп прироста,      %			Абсолютное содержание 1% прироста, тыс. чел.
		цеп	баз		цеп	баз		цеп	баз		цеп	баз
1995	37083	—	—		—	—		—	—		—	—		—
2000	38411	1328	1328		1,0358	1,0358		103,58	103,58		3,58	3,58		370,83
2005	38313	-98	1230		0,9974	1,0332		99,74	103,32		-0,26	3,32		384,11
2007	38467	154	1384		1,0040	1,0373		100,40	103,73		0,40	3,73		383,13
2008	38598	131	1515		1,0034	1,0409		100,34	104,09		0,34	4,09		384,67

3. Определим среднюю численность пенсионеров в исследуемый период. Средний уровень интервального ряда с разностоящими уровнями вычисляется по формуле средней арифметической взвешенной:

(тыс.чел.)


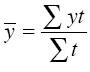
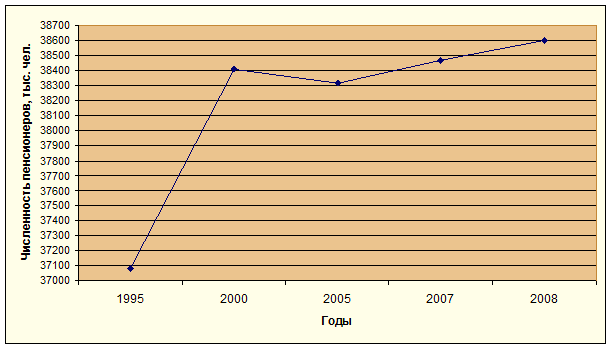
4. По данным таблицы постройте динамический график численности пенсионеров в исследуемый период.

Тула – 2023