Лаб 3. лаб 3 Плотникова Б8119-09.03.04прогин. Программная инженерия
 Скачать 102.61 Kb. Скачать 102.61 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «Дальневосточный федеральный университет» ШКОЛА ЕСТЕСТВЕННЫХ НАУК Кафедра прикладной математики, механики, управления и программного обеспечения ПРАКТИЧЕСКАЯ РАБОТА на тему «Алгоритмы сортировки» по дисциплине «Фундаментальные структуры данных и алгоритмы» Специальность 09.03.04 «Программная инженерия» Выполнил: студент гр. Б8119-09.03.04прогин ____________Плотникова Е. А. Проверила: старший преподаватель ____________Крестникова О.А. г. Владивосток, 2021 Неформальная постановка задачиРеализовать сортировку бинарными вставками, сортировку восходящим слиянием. Проверить на устойчивость. Сравнить по времени, числу обменов, числу сравнений. Определить последовательности, на которых достигается наихудшее и наилучшее значение времени. Описание алгоритма.Сортировка слиянием реализована итеративно (восходящее). Алгоритм функции SSort: int step = 1 – шаг разбиения = 1 while (step < n) – пока шаг меньше длины массива int index = 0; – индекс результирующего массива. int l = 0; – левая граница участка int m = l + step; – середина участка int r = l + step * 2; – правая граница участка. Do - выполнять m = m < n ? m : n; r = r < n ? r : n; – сортируемый участок не выходит за границы последовательности. int i1 = l, i2 = m; – индексы сравниваемых элементов. for (; i1 < m && i2 < r; ) – пока i1 не дошёл до середины и i2 не дошёл до конца S_comp++; - увеличить количество сравнений на 1. если (a[i1] < a[i2]) temp[index++] = a[i1++]; иначе temp[index++] = a[i2++]; – заполняем участок результирующей последовательности Пока (i1 < m) temp[index++] = a[i1++]; – заносим оставшиеся элементы сортируемых участков Пока (i2 < r) temp[index++] = a[i2++]; – заносим оставшиеся элементы сортируемых участков l += step * 2; m += step * 2; r += step * 2; – перемещаемся на следующий сортируемый участок } пока (l < n); – пока левая граница сортируемого участка - в пределах последовательности Цикл for (int i = 0; i < n; i++) a[i] = temp[i]; – переносим сформированный массив обратно в a step *= 2; – увеличиваем в 2 раза шаг разбиения } } Текст Программы #include #include #include #include using namespace std; int S_comp = 0; void SSort(int* a, int n) { int step = 1; int* temp = (int*)malloc(n * sizeof(int)); while (step < n) { int index = 0; int l = 0; int m = l + step; int r = l + step * 2; do { m = m < n ? m : n; r = r < n ? r : n; int i1 = l, i2 = m; for (; i1 < m && i2 < r; ) { S_comp++; if (a[i1] < a[i2]) { temp[index++] = a[i1++]; } else { temp[index++] = a[i2++]; } } while (i1 < m) { temp[index++] = a[i1++]; } while (i2 < r) { temp[index++] = a[i2++]; } l += step * 2; m += step * 2; r += step * 2; } while (l < n); for (int i = 0; i < n; i++) a[i] = temp[i]; step *= 2; } } int binarySearch(int arr[], int last, int x, int& comp) { int l = 0;//первый элемент int r = last;//последний while (l < r) { int m = (l + r) / 2;//берем середину comp++; if (x < arr[m]) {//если вставляемый элемент меньше r = m; } else { l = m + 1; } } comp++; if (l == r) {//если середина comp++; if (arr[l] < x) {//если вставляемый элемент больше середины return l + 1;//вставляем влево } else { return l; } } return l; } //сортировка вставка void insertionSort(int arr[], int size) { float time = (float)clock(); int comp = 0; int perm = 0; bool stable; for (int i = 0; i < size - 1; i++) { if (arr[i] < arr[i + 1]) { stable = true; } else { stable = false; } int eltoplace = arr[i + 1]; int place = binarySearch(arr, i, eltoplace, comp);//ищем место для вставки бинарным поиском for (int j = i; j >= place; j--) {//передвигаем элементы вправо для вставки perm++; arr[j + 1] = arr[j]; } perm++; arr[place] = eltoplace; } cout << "Сравнения: " << comp << " Обмены: " << perm << endl; cout << "Время: " << ((float)clock() - (float)time) / CLOCKS_PER_SEC << " секунд" << endl; if (stable) { cout << "Устойчива" << endl << endl; } else { cout << "Не устойчива" << endl << endl; } } int main() { } ТестированиеРазмер 1. 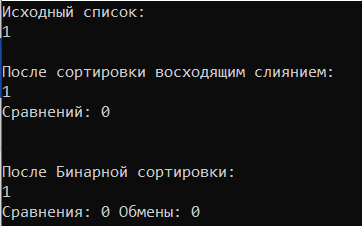 Размер 9. 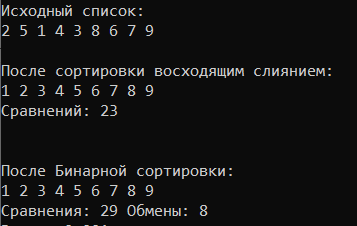 Размер 9. Повторяющиеся элементы. 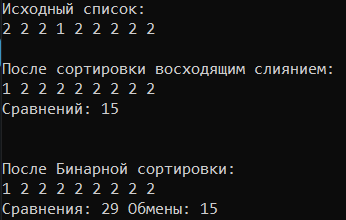 Размер 2. 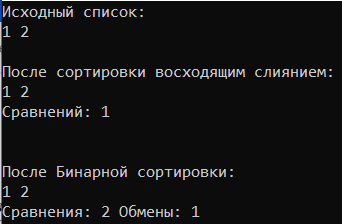 Наилучшие и наихудшие последовательности, устойчивость:Бинарная сортировка работает достаточно быстро, если сортируемые ключи состоят из абсолютно случайных битов. Потенциальная проблема, которая может возникнуть при использовании бинарной сортировки: довольно часто могут встречаться вырожденные разбиения (когда все ключи имеют одно и то же значение разряда, по которому производится разбиение). С сортировкой восходящим слиянием во всех случаях время её работы стремится к линейно-логарифмической величине. По этому параметру она схожа с пирамидальной сортировкой, которая, в свою очередь, выигрывает у сортировки слиянием по количеству необходимой памяти. Поэтому о наилучших и наихудших вариантах последовательностей для сортировки слиянием корректно говорить лишь в случае сравнения с другими алгоритмами сортировки. Таким образом, на почти упорядоченной последовательности сортировка вставками будет иметь время работы, близкое к линейному. Будем считать, что для сортировки слиянием такой вариант последовательности будет наихудшим. Продолжая сравнительный анализ времени работы сортировок на одинаковых последовательностях, рассмотрим алгоритм бинарной сортировки и алгоритм сортировки восходящим слиянием. В таком случае наихудшей последовательностью чисел для бинарной сортировки является отсортированная последовательность. При этом время её работы будет являться квадратичной функцией. В силу независимости времени работы сортировки слиянием от исходного набора, будем считать, что такая последовательность является наилучшей. В тесте на устойчивость введем последовательность одинаковых чисел. 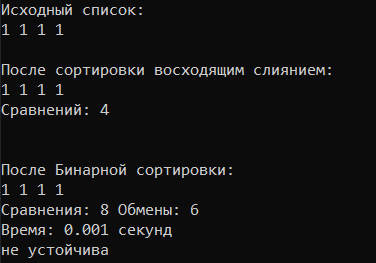 Таким образом, при исходной последовательности, состоящей из одинаковых элементов, бинарная сортировка произвела операции обмена. Сортировка слиянием в силу своей особенности не производит обменов. Следовательно, сортировка слиянием является устойчивой, а бинарная – неустойчивой. |
