конспект. Конспект урока. Прогре

• Название: Прогре
• Анкор: конспект
• Дата: 08.03.2023
• Размер: 193.59 Kb.
• Имя файла: Конспект урока.docx
• Тип: Документы; #974473
• страница: 2 из 3

Итоги работы первой группы докладывают «теоретики»: а₁= а, - первоначальный вклад;


2р

3р
а₂= а+ ₁₀₀ а; а₃= а+ ₁₀₀ а;

а₄= а+ ₁₀₀ а; . . .


tр
а_t+1 = а+ ₁₀₀ а

Что можно сказать о математической модели этой ситуации?

Вывод: математическая модель этой ситуации является арифметической прогрессией.


р
а₁= а- первоначальный вклад;

d= ₁₀₀ а;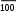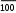

a_t+1= а+ ^tра= а∙(1+ ^tр) руб. можно получить за t лет – формула

простых процентов. (Появляется на стенде).

Рассмотрим математическую модель второй ситуации, докладывают «теоретики» второй группы:

Вы решили прийти в банк только в конце срока хранения вклада. b₁= b– первоначальный вклад;

b₂= b₁+₁₀₀ b= b₁∙(1+₁₀₀ );

b₃= b₁∙(1+₁₀₀ ) (1+₁₀₀ )= b(1₁₀₀)²;


р

1
b₄= b(1₁₀₀)³; . . .


р

1
b_t= b(1₁₀₀)^t

Что можно сказать о математической модели этой ситуации?

Вывод: математическая модель этой ситуации является геометрической прогрессией.


р
b₁= b– первоначальный вклад;

q= 1 + ₁₀₀ ;

3


р

1
b_t= b(1₁₀₀)^tрублей можно получить за t лет - формула сложных процентов. (Появляется на стенде).

Задача 1 предлагается для решения в первой группе.

Вкладчик открыл в банке счет и положил на него 180000 руб. сроком на 4 года под простые проценты по ставке 15% в год. Какой будет сумма, которую вкладчик получит при закрытии вклада? На сколько рублей вырастет вклад за 4 года?

Решение:

а= 180000 руб.; t = 4; р= 15%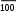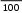

_{1) а}5_{= а(1+} 4р_{) = 180000∙(1+}415_{) = 180000∙1,6 = 288000 руб.}

2) 288000-180000 = 108000 руб. Ответ: 288000 рублей, 108000 рублей.

Задача 2 предлагается для решения во второй группе.

Вкладчик открыл в банке счет и положил на него 180000 руб. сроком на 4 года под сложные проценты по ставке 15% в год. Какой будет сумма, которую вкладчик получит при закрытии вклада? На сколько рублей вырастет вклад за 4 года?

Решение:


р 15
b₁= 180000 руб.; t = 4; р= 15%


1
1) b₅= b(1₁₀₀)⁴ = 180000(1₁₀₀)⁴=180000∙1,15⁴=180000∙1,749≈314821 руб.

2) 314821 – 180000=134821 руб. Ответ: 314821 рубль, 134821 рубль.

Результаты решения задач докладываются учащимися-«аналитиками».

Почувствуйтеразницу!

Какой видпроцентоввыгоднее?

Дополнительные вопросы:

 Если через тот же срок при том же первоначальном вкладе вкладчик хочет получить не 288000 рублей, а 3000000 рублей то, что можно определить по формуле простых процентов?

(Можно определить количество р процентов, т.е. поискать другой банк с нужными р% годовых.)

 Можно ли определить по формуле простых процентов, какую сумму нужно положить в тот же банк под те же простые проценты, чтобы через 5 лет он достиг суммы 100000 рублей?

4

Задача 3 предлагается для решения в обеих группах

Предположим, что в 1776 году, когда образовались США, 1 доллар был отдан под 10% годовых. В какую сумму он превратился к 1976 году – 200-летней годовщине образования США?

Формула каких процентов (простых или сложных ) здесь может быть применена? (Сложных процентов)

Решение: 1∙(1+0,1)²⁰⁰=1,1²⁰⁰=((1,1)⁸)²⁵≈(2,14)²⁵2²⁵=2¹⁰∙2¹⁰∙2⁵=1024∙1024∙3232000000 Ответ: более 32000000 долларов.

Вывод:вложив1доллар можнораспоряжатьсямиллионами!

Сложные проценты обладают удивительным свойством – с возрастание


р
показателя t величина (1₁₀₀)^tдостигает колоссальных размеров. Попробуйте объяснить это.