экзамен математика. ответы. Производная функции. Дифференцирование суммы, разности, произведения и частного двух функций. Геометрический смысл производной функции
 Скачать 253.03 Kb. Скачать 253.03 Kb.
|
1 2 Кривая второго порядка может быть задана уравнениемАх2 + 2Вху + Су2 + 2Dx + 2Ey + F = 0. Существует система координат (не обязательно декартова прямоугольная), в которой данное уравнение может быть представлено в одном из видов, приведенных ниже. 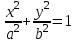 - уравнение эллипса. - уравнение эллипса.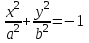 - уравнение “мнимого” эллипса. - уравнение “мнимого” эллипса.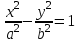 - уравнение гиперболы. - уравнение гиперболы.a2x2 – c2y2 = 0 – уравнение двух пересекающихся прямых. y2 = 2px – уравнение параболы. y2 – a2 = 0 – уравнение двух параллельных прямых. y2 + a2 = 0 – уравнение двух “мнимых” параллельных прямых. y2 = 0 – пара совпадающих прямых. (x – a)2 + (y – b)2 = R2 – уравнение окружности. Окружность В окружности (x – a)2 + (y – b)2 = R2 центр имеет координаты (a; b).Эллипс, его свойства и изображение. Эллипс. Определение. Эллипсом называется линия, заданная уравнением 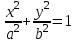 . .Определение. Фокусами называются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина. 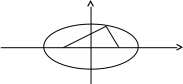 у уМr1 r2 F1 O F2 х F1, F2 – фокусы. F1 = (c; 0); F2(-c; 0) с – половина расстояния между фокусами; a – большая полуось; b – малая полуось. Свойства: Эллипс пересекает каждую из осей координат в двух точках. 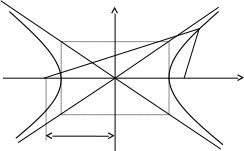 Сумма расстояний от любой точки эллипса до его фокусов есть величина постоянная и равная удвоенной большей полуоси. Сумма расстояний от любой точки эллипса до его фокусов есть величина постоянная и равная удвоенной большей полуоси.Эллипс имеет две взаимно перпендикулярные оси симметрии. Эллипс имеет две взаимно перпендикулярные оси симметрии. Центр симметрии эллипса называется центром эллипса. Эллипс может быть получен сжатием окружности. Гипербола, её свойства и изображение. 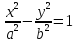 Определение. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами. По определению r1 – r2= 2a. F1, F2 – фокусы гиперболы. F1F2 = 2c. Свойства: Гипербола не имеет общих точек с осью Oy, а ось Ox пересекает в двух точках A (a; 0) и B (–a; 0), которые называются вершинами гиперболы. Гипербола имеет две взаимно перпендикулярные оси симметрии. Гипербола имеет центр симметрии. Гипербола пересекается с прямой y = kx при |K|< b/a в двух точках. Если K| >= b/a то общих точек у прямой и гиперболы нет. Парабола, её свойства и изображение. Определение. Параболой называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус. Расположим начало координат посередине между фокусом и директрисой. 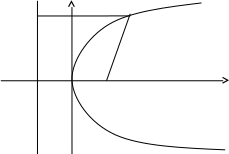 у у А М(х, у) А М(х, у) О F x   p/2 p/2 Величина р (расстояние от фокуса до директрисы) называется параметром параболы. Выведем каноническое уравнение параболы. Y2=2px Свойства: Парабола имеет ось симметрии. Парабола расположена в полуплоскости x ≥ 0. Системы координат в пространстве. декартовы, цилиндрические и сферические координаты Декартова система координат в пространстве определяется точкой и базисом из трех векторов. Точка O называется началом координат. Прямые, проведенныечерез начало координат в направлении базисных векторов, называются осями координат. В трехмерном пространстве они называются осями абсцисс, ординат и аппликат. Оси координат являются числовыми осями с началом в точке O , положительным направлением, совпадающим с направлением соответствующего базисного вектора, и единицей длины, равной длине этого вектора. Координатами точки M называются координаты вектора OM ( радиус–вектора) (см. рис. 1). Если базис ортонормированный, то связанная с ним декартова система координат называется прямоугольной. В цилиндрических координатах положение точки M определяется числами ρ , j и z , где ρ и j — полярные координаты точки M' , а z — проекция вектора OM на вектор →n . В сферических координатах положениеточки M определяется числами ρ , j и θ , где ρ = |OM| , j — полярный угол точки M' , а θ — угол между векторами →n и OM .Мы будем отсчитывать угол θ от вектора →n по направлению к вектору OM . Угол θ принимает значения от 0 до π . Уравнения плоскости в пространстве. Условия пересечения, параллельности, совпадения и перпендикулярности двух плоскостей в пространстве. Определение угла между двумя плоскостями. Каноническое уравнение плоскости в пространстве: Аx+By+Cz+D=0, где D = -Ax0-By0-Cz0 Условие параллельности двух плоскостей 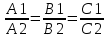 Условие перпендикулярности A1*A2+B1*B2+C1*C2=0 Плоскости совпадают когда 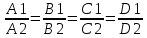 угол между плоскостями находится по формуле: 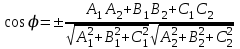 Расстояние d от точки Мo(Xo;Yo;Zo) до плоскости Ax+By+Cz+D=0 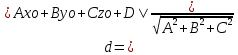 Уравнения прямой в пространстве. Условия пересечения, параллельности, совпадения и перпендикулярности двух прямых в пространстве. Определение угла между двумя прямыми. Параметрические уравнения прямой в пространстве: 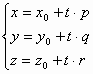 Канонические уравнения прямой в пространстве : 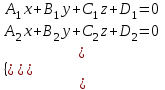 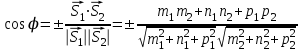 . .32.Поверхности второго порядка, их классификация и изображения Определение. Поверхности второго порядка – это поверхности, уравнения которых в прямоугольной системе координат являются уравнениями второго порядка. Цилиндрические поверхности. Определение. Цилиндрическими поверхностями называются поверхности, образованные линиями, параллельными какой- либо фиксированной прямой. 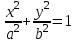 - эллиптический цилиндр. - эллиптический цилиндр.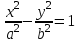 - гиперболический цилиндр. - гиперболический цилиндр.x2 = 2py – параболический цилиндр. Поверхности вращения. Определение. Поверхность, описываемая некоторой линией, вращающейся вокруг неподвижной прямой d, называется поверхностью вращения с осью вращения d. 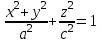 - эллипсоид вращения - эллипсоид вращения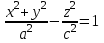 - однополостный гиперболоид вращения - однополостный гиперболоид вращения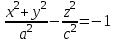 - двуполостный гиперболоид вращения - двуполостный гиперболоид вращения 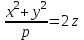 - параболоид вращения - параболоид вращенияСфера: 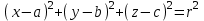 Трехосный эллипсоид: 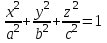 Однополостный гиперболоид: 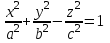 Двуполостный гиперболоид: 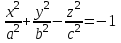 Эллиптический параболоид: 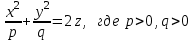 Гиперболический параболоид: 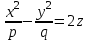 Конус второго порядка: 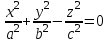 Определение. Цилиндрическими координатами точки М называются числа (r, , h), которые определяют положение точки М в пространстве. Определение. Сферическими координатами точки М называются числа (r,,), где - угол между и нормалью. 1 2 |
